数据结构(邓俊辉)学习笔记】优先级队列 07——堆排序
1.算法
作为完全二叉堆的一个应用,这节来介绍堆排序算法。

是的,谈到优先级队列,我们很自然地就会联想到排序。因为就其功能而言,包括完全二叉堆在内的任何一种优先级队列都天生地具有选取功能,也就是选取其中的最大元。因此,很自然地就会联想起选择排序。
还记得这样一幅插图(上图中右上图),我们曾经用它来解释选择排序的原理及过程。不妨温习一下,在选择排序算法中,我们始终将整个序列分为两部分,也就是左侧的待排序部分以及右侧的已排序部分。而且前者中的任何一个元素都不大于后者中的任何一个元素。因此我们只需反复地遍历待排序元素,从中选取出最大者,并将它加入到已排序的子序列中。是的,正因为我们每次都需要对待排序的部分作遍历,从而导致每次选取都需要线性的时间,以致整个算法累计需要平方量级的时间。
究其原因,可以理解为我们当初对数据结构的理解和掌握还非常有限,以至于我们只能借助简单的数据结构来组织待排序的元素。而经过了一段时间的学习之后,我们已经今非昔比,我们可以运用更为高级的数据结构来组织这些待排序的元素,从而实现更高的选取效率。
比如,联想到我们刚刚学过的内容,很自然地就会想到用一个完全二叉堆来取代此前简单的线性结构。如果暂时忽略底层的具体实现,我们就会发现整个算法流程可以基本保持不变。
- 此前在与预处理阶段对整个线性序列的初始化,在这里则对应于建堆操作。我们刚刚介绍过,如果采用 Floyd 算法,这一步只需线性的时间。
- 接下来我们需要反复地取出最大元,也就是整个堆当前的堆顶。我们知道, delMax操作每次只需 log n 的时间。没错,log n 而不再是 n。因此,整个算法的复杂度,也就应该是 n log n,而不再是 n 2 n^2 n2。
当然,此前的不变性依然保持,也就是待排序的部分始终都不超过已排序部分,因此算法的正确性依然可以得到保证。那么难道这个算法就是这样的平淡无奇?不是的,事实上堆排序的奥妙还不止于此,比如在空间复杂度方面,堆排序算法还可以做得更好。
2.就地

准确地讲,在空间复杂度方面,我们希望堆排序算法能够做到就地,也就是除了输入数据以外,只需要常数的辅助空间。 这种构思是有可能实现的,因为我们注意到,所谓的完全二叉堆在物理上就是不折不扣的向量。
因此我们或许可以令完全二叉堆与已排序的部分在同一个向量中和平共处,经过精巧的设计,我们的确可以将这一构想兑现为这种形式,具体来说,已排序部分依然居于向量的后端,而与之互补的前缀则恰好构成一个完全二叉堆,如果沿用大顶堆的惯例,我们可以立即发现,堆中的最大元必然始终都是0号元素,而接下来需要与之兑换的 X,则必然是相对于已排序元素而言秩为 -1 的那个元素。
按照以上堆排序的初始版本,我们首先需要取出这个最大的元素,然后用 x 来取而代之,然后再将备份的最大元植入 x 这个位置。当然,为了算法能够继续持续下去,我们还需要对新的根节点做下滤调整。
对于这样的连续4步操作,你能发现有什么可以优化的地方吗?
是的,这里的1、2、3完全可以整合起来,只需 m 和 x 之间的一次兑换即可等效地完成。因此,算法过程中的每一步迭代可以进一步的规整为两大步骤,也就是第一步交换,以及第二步下滤。是的,反复地交换下滤,交换下滤。直至堆变空。在整个算法的过程中,除了交需要用到常数个辅助空间之外,我们并不需要任何更多的辅助空间。
以上过程可以描述为这样的伪代码(上图最下面行),但是它又如何进一步地实现为真正的代码呢?
3.实现

在这里,给出堆排序的一个更为通用的算法版本,也就是说对于任何的向量,这个算法都可以对其中任意指定的区间进行排序。
- 作为初始化,首先需要调用完成二叉堆的建堆算法,在线性的时间内,将向量的这个区间整理为一个完全二叉堆。
- 此后进入反复迭代,请留意这个迭代所具有的不变性,也就是完全二叉堆当前所在的区间是由 lo 和 hi 界定的,按照我们一直以来采用的惯例,lo 所对应的是堆的首元素,而 hi 所指示的则是这个堆尾部的哨兵。
因此在每一步迭代中,我们都只需取出首元素位置处的最大元,并且将它与末元素交换,而新的堆顶元素的下滤功能则同样是由 delMax 在底层完成。
4.实例

看堆排序算法的一个具体实例,考察这样一个规模为 5 的向量,首先从逻辑上将它视作为一棵完全二叉树,其中有两个内部节点,也就是2和4,于是我们采用 Floyd 算法分别对 2 和 4分别做一趟下滤,即可最终得到这样一个完全二叉堆。至此,也就完成了算法的预处理步骤。

接下来我们进入算法的主体循环,请注意在一开始整个向量都是未排序的部分,而已排序的部分初始为空。即便如此,我们依然可以使用算法的基本策略,也就是令当前的堆顶与末元素互换位置。
-
破坏之后的瞬间应该是这样(上图上左二)。原来的末元素2成为了堆顶,而5则在逻辑上从原来的堆中分离出来,加入原本为空的 S。也就是说,已排序的序列此时已经拥有了第一个元素。
-
当然,我们还需要对新的堆顶做下滤调整,从而使得剩下的 4 个元素依然恢复为一个堆,尽管规模减少了一个单位。不出意外,接下来的最大元 4 也自然成为了新的堆顶(上图上左三)。
-
因此在下一轮迭代中,我们依然是将这个新的堆顶与当前的末元素互换位置,在逻辑上这等效于将堆顶摘出,并归入到有序序列中(上图下左一)。
-
同样,我们仍需对新的根节点做一次下滤调整,从而使得剩余的三个元素能够继续保持为是一个合法的大顶堆(上图下左三)。

-
不出预料,当前尚未排序的元素中的最大者 3 此时也必然就是堆顶。因此,我们也只需令它与当前的末元素 2 做一次兑换。在逻辑上,这依然等同于将这个堆顶摘出并归入到有序列中。
-
此后再经过一轮下滤调整,剩余的元素也依然会恢复为一个合法的大顶堆,尽管此时已经只剩最后的两个元素了。
相关文章:

数据结构(邓俊辉)学习笔记】优先级队列 07——堆排序
1.算法 作为完全二叉堆的一个应用,这节来介绍堆排序算法。 是的,谈到优先级队列,我们很自然地就会联想到排序。因为就其功能而言,包括完全二叉堆在内的任何一种优先级队列都天生地具有选取功能,也就是选取其中的最大…...

npm install pnpm -g 报错的解决方法
npm install pnpm -g 报错的解决方法 npm error code ETIMEDOUT npm error errno ETIMEDOUT npm error network request to https://registry.npmjs.org/pnpm failed, reason: npm error network This is a problem related to network connectivity. npm error network In mo…...

集师知识付费小程序开发
智慧生活,从选择一款优质知识付费小程序起航 在这个信息爆炸的时代,知识成为了最宝贵的财富。我们渴望不断学习,提升自我,追求更高品质的生活。而一款优质的知识付费小程序,就如同照亮前行道路的明灯。 它是知识的宝库…...

前端开发提效工具——用户自定义代码片段
做开发总是会有大量的代码要写,但是有时候某些代码是非常基础但是很多,我们就可以把这一部分整合起来,使用一个很简短的关键字来快速唤出。 如何新建这样的代码段? 1.在VSCode当中找到Snippets,然后点击 2.之后会弹出…...
docker容器安全加固参考建议——筑梦之路
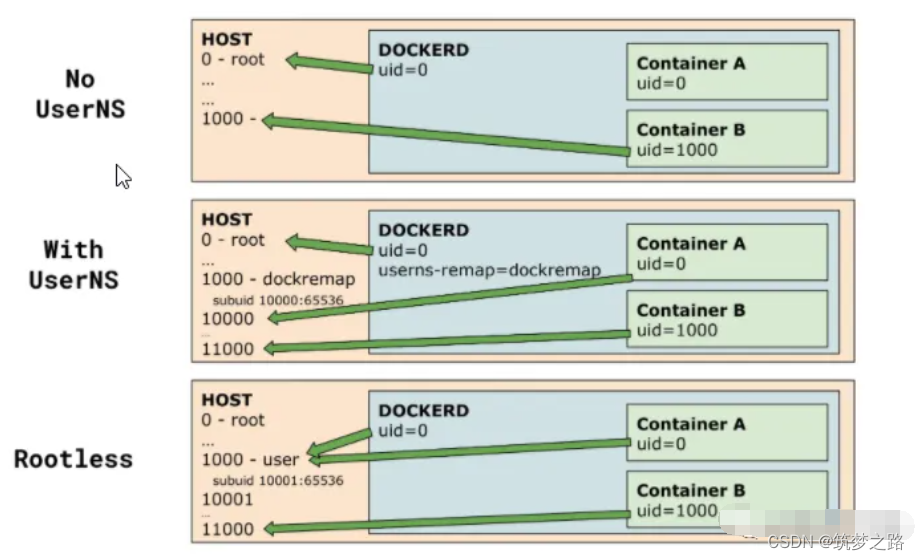
这里主要是rootless的方案。 在以 root 用户身份运行 Docker 会带来一些潜在的危害和安全风险,这些风险包括: 容器逃逸:如果一个容器以 root 权限运行,并且它包含了漏洞或者被攻击者滥用,那么攻击者可能会成功逃出容器…...
基于 Appium 的 App 爬取实战
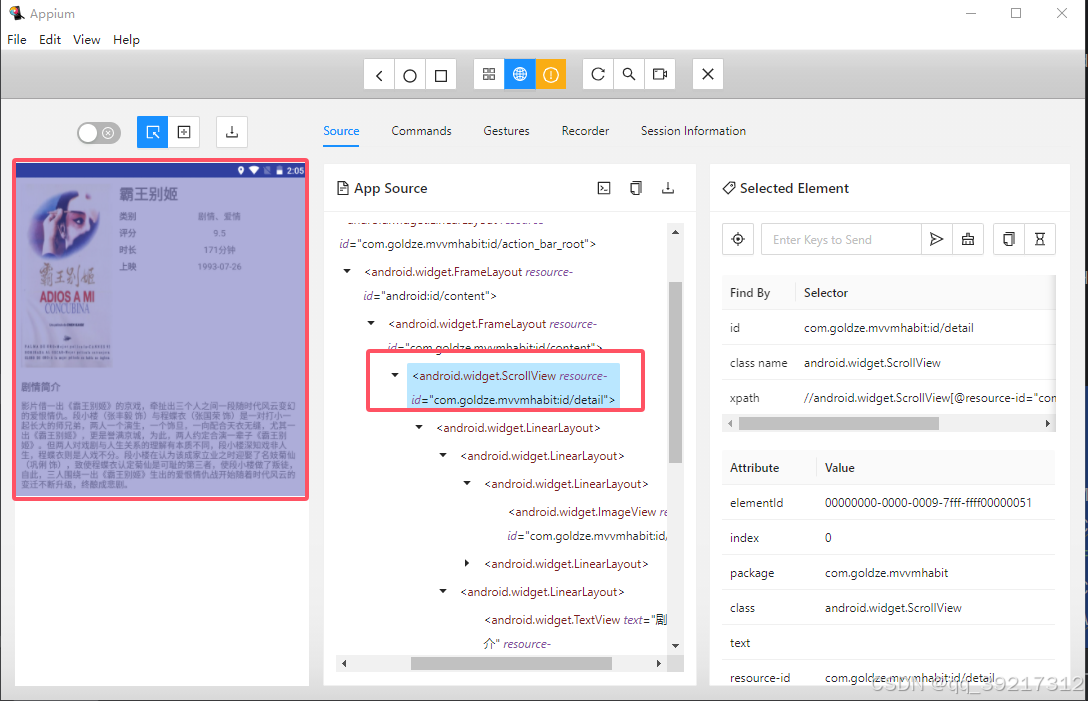
除了运行 Appium 的基本条件外,还要一个日志输出库 安装: pip install loguru 思路分析 首先我们观察一下整个 app5 的交互流程,其首页分条显示了电影数据, 每个电影条目都包括封面,标题, 类别和评分 4…...

nvm与node安装
参考: 一文搞定NVM安装所有问题NVM UI解决nodejs下载慢问题 node_mirror: http://npmmirror.com/mirrors/node/ npm_mirror: http://registry.npmmirror.com/mirrors/npm/解决nvm list available报错问题 Could not retrieve https://npm.taobao.org/mirrors/node/…...

【电子通识】什么是MSL湿敏等级
潮敏失效是塑料封装表贴器件在高温焊接工艺中表现出来的特殊的失效现象。 造成此类问题的原因是器件内部的潮气膨胀后使得器件发生损坏。 MSL是“Moisture Sensitivity Level(湿气敏感性等级)”的缩写,针对需进行回流焊的产品设定了MSL基准。…...

【ARM 芯片 安全与攻击 5.4 -- Meltdown 攻击与防御介绍】
文章目录 什么是 Meltdown 攻击?Meltdown 攻击的基本原理Meltdown 攻击代码示例Meltdown 攻击在芯片中的应用应用场景Meltdown 攻击与瞬态攻击、测信道攻击的关系针对 Meltdown 攻击的防御硬件级防御Summary什么是 Meltdown 攻击? Meltdown 攻击是一种利用处理器乱序执行(o…...

Django 后端架构开发:分页器到中间件开发
🚀 Django 后端架构开发:分页器到中间件开发 🚀 🔹 应用样式:上下翻页 分页功能在处理大量数据时非常有用。通过上下翻页,我们可以让用户轻松浏览数据。以下是一个展示产品列表的分页示例: fr…...

亲测解决The client socket has failed to connect to
这个问题是因为深度学习的程序(服务)跟本地主机连接不上,解决方法是确认rank起始数为0。 报错原文 [W socket.cpp:663] [c10d] The client socket has failed to connect to [csdn-xiaohu]:12345 (errno: 22 - Invalid argument).解决方法 …...

Intel ACRN 安装WIN10 VM
上一篇帖子记录了ACRN运行rt linux,这篇帖子记录一下最近倒腾出来的WIN10。目前架构如下 ACRN可以把它理解为一个基于Linux类似软件的Type1 Hypervisor,基于Linux去做而不是baremetal是为了更方便去配置资源。 首先我们得有两台电脑,一台是开…...

贷齐乐案例
源码分析: <?php // 设置 HTTP 头部,指定内容类型为 text/html,字符集为 utf-8 header("Content-type: text/html; charsetutf-8"); // 引入数据库配置文件 require db.inc.php; // 定义函数 dhtmlspecialchars,用…...

[Qt][Qt 网络][下]详细讲解
目录 1.TCP Socket1.核心API概览2.回显服务器3.回显客户端 2.HTTP Client3.其他模块 1.TCP Socket 1.核心API概览 核⼼类是两个:QTcpServer和QTcpSocketQTcpServer用于监听端口,和获取客户端连接 listen(const QHostAddress&, quint16 port)&#…...

十三、OpenCVSharp的目标检测
文章目录 简介一、传统目标检测方法1. 基于滑动窗口的检测2. 特征提取与分类器结合(如 HOG + SVM)3. 级联分类器二、基于深度学习的目标检测1. YOLO 系列算法2. SSD 算法3. Faster R-CNN 算法三、深度学习目标检测模型的训练和部署四、目标检测的性能评估指标1. 准确率、召回…...

STM32标准库学习笔记-6.定时器-输入捕获
参考教程:【STM32入门教程-2023版 细致讲解 中文字幕】 定时器输入捕获 IC(Input Capture)输入捕获输入捕获模式下,当通道输入引脚出现指定电平跳变时,当前CNT的值将被锁存到CCR中,可用于测量PWM波形的频率…...

vue前端可以完整的显示编辑子级部门,用户管理可以为用户分配角色和部门?
用户和角色是一对多的关系用户和部门是多对多得关系<template><div class="s"><!-- 操作按钮 --><div class="shang"><el-input v-model="searchText" placeholder="请输入搜索关键词" style="width:…...

量化交易的基石:ExchangeSdk
作为长期混迹在合约市场的老韭菜来说,已不能满足与手动下单来亏钱,必须得通过脚本来加速,为了达到这个目的就产生了项目。目前封装的主要是合约的API接口,不支持现货交易。 Github: https://github.com/silently9527/exchange-sdk…...

【区块链+金融服务】基于区块链的一站式绿色金融开放平台 | FISCO BCOS应用案例
科技的进步为绿色金融发展提供了新的机遇,但银行、企业、第三方金融机构等在进行绿色金融业务操作过程中, 存在着相关系统和服务平台建设成本高、迭代难度大、数据交互弱、适配难等痛点。 基于此,中碳绿信采用国产开源联盟链底层平台 FISCO …...

使用Python实现深度学习模型:智能娱乐与虚拟现实技术
介绍 智能娱乐与虚拟现实(VR)技术正在改变我们的娱乐方式。通过深度学习模型,我们可以创建更加沉浸式和智能化的娱乐体验。本文将介绍如何使用Python和深度学习技术来实现智能娱乐与虚拟现实的应用。 环境准备 首先,我们需要安装一些必要的Python库: pip install pand…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...
