【数学分析笔记】第2章第1节实数系的连续性(1)
2. 数列极限
2.1 实数系的连续性
人类对数系认识的历史:
人类最早对数系的认识是自然数集合 N \mathbb{N} N,自然数系对加法和乘法是封闭的(这里的封闭是指:若 m ∈ N , n ∈ N ⇒ m + n ∈ N , m n ∈ N m\in\mathbb{N},n\in\mathbb{N}\Rightarrow m+n\in\mathbb{N},mn\in\mathbb{N} m∈N,n∈N⇒m+n∈N,mn∈N),但是对减法来说,自然数集合 n \mathbb{n} n不封闭,数系 n \mathbb{n} n不够了,人类就把数系扩充到整数集合 Z \mathbb{Z} Z,整数集合 Z \mathbb{Z} Z对加法,乘法,减法封闭,但是对除法不封闭,于是人类又把数集扩充到有理数集 Q \mathbb{Q} Q,有理数集合 Q \mathbb{Q} Q对加减乘除都是封闭的,有很长一段时间人类觉得有理数集合很完美,后来古希腊的毕达哥拉斯学派发现有理数集合对开方不封闭,毕达哥拉斯学派认为任意两条线段都是可公度的(有a,b两个线段, a , b a,b a,b表示两个线段的长度,则存在另一长度为 c c c的线段使得 a = m c , b = n c ( m , n ∈ N ) ⇒ a b = m n a=mc,b=nc(m,n\in\mathbb{N})\Rightarrow\frac{a}{b}=\frac{m}{n} a=mc,b=nc(m,n∈N)⇒ba=nm),但是这套理论建立在任意两个线段可公度的前提下,正方形边长为1,正方形的对角线和边长不可公度( 2 1 \frac{\sqrt{2}}{1} 12不能等于 m n , m , n ∈ N \frac{m}{n},m,n\in\mathbb{N} nm,m,n∈N),这是数学史上的第一次危机,于是我们有了一个命题。
【命题】 2 \sqrt{2} 2不是有理数。
【证】用反证法,假设 2 \sqrt{2} 2是有理数,即 2 = n m , m , n ∈ Z , 且 m , n \sqrt{2}=\frac{n}{m},m,n\in\mathbb{Z},且m,n 2=mn,m,n∈Z,且m,n互质, 2 = n 2 m 2 2=\frac{n^{2}}{m^{2}} 2=m2n2,即 n 2 = 2 m 2 n^{2}=2m^{2} n2=2m2,由于 2 m 2 2m^{2} 2m2是偶数(2是偶数,偶数×偶数还是偶数,偶数×奇数还是偶数,所以说明 2 m 2 2m^{2} 2m2是偶数则 n 2 n^{2} n2是偶数,而 n 2 = n × n n^{2}=n\times n n2=n×n,在上述情况中,如果两个一样的整数相乘是偶数,那么只有偶数×偶数的情况,因为偶数×奇数的情况下对应的是两个不一样的数,所以 n n n是偶数),所以 n n n是偶数,令 n = 2 k , k ∈ Z n=2k,k\in\mathbb{Z} n=2k,k∈Z,则 n 2 = 4 k 2 = 2 m 2 n^{2}=4k^{2}=2m^{2} n2=4k2=2m2,则 m 2 = 2 k 2 m^{2}=2k^{2} m2=2k2,所以 m m m是偶数(和刚才的 n n n是偶数的推理过程是一样的),由于 m , n m,n m,n互质,但是 m , n m,n m,n都是偶数,矛盾(偶数和偶数是不互质的,都是能约分的,至少有公因子2),所以 2 \sqrt{2} 2不是有理数。

由此说明在有理数集合 Q \mathbb{Q} Q中开根号不封闭,所以人类要扩充数系。
有理数可以表示为有限小数或无限循环小数,把无限不循环小数加到有理数集合里面去这样就使得开方也变得封闭,它可以完全布满整个数轴,不留“空隙”,我们将无限不循环小数定义为无理数,把无理数加入到有理数集合中构成实数集合 R = { x ∣ x 是有理数或无理数 } \mathbb{R}=\{x|x是有理数或无理数\} R={x∣x是有理数或无理数},实数所对应的点布满了整个数轴,它上面没有“空隙”,我们将这个性质称之为实数的连续性。实数集合又叫实数连续统。
2.1.1 最大数与最小数
S ⊂ R , S ≠ ∅ \textbf{S}\subset\mathbb{R},\textbf{S}\ne\emptyset S⊂R,S=∅,若 S \textbf{S} S是有限集, S \textbf{S} S必有最大数与最小数,但若 S \textbf{S} S是无限集,则 S \textbf{S} S不一定有最大数与最小数。
先引入记号: ∀ \forall ∀与 ∃ \exists ∃, ∀ \forall ∀表示“对于任意的”或者“对于每一个”, ∃ \exists ∃表示“存在”或“可以找到”
若 S ⊂ R , S ≠ ∅ \textbf{S}\subset\mathbb{R},\textbf{S}\ne\emptyset S⊂R,S=∅,若 ∃ ξ ∈ S \exists\xi\in\textbf{S} ∃ξ∈S,使得 ∀ x ∈ S \forall x\in\textbf{S} ∀x∈S,有 x ≤ ξ x\le \xi x≤ξ,则称 ξ \xi ξ是 S \textbf{S} S中的最大数,记为 ξ = max S \xi=\text{max}\textbf{S} ξ=maxS,若 ∃ η ∈ S \exists\eta\in\textbf{S} ∃η∈S,使得 ∀ x ∈ S \forall x\in\textbf{S} ∀x∈S,有 x ≥ η x\ge \eta x≥η,则称 η \eta η是 S \textbf{S} S中的最小数,记为 η = min S \eta=\text{min}\textbf{S} η=minS
【例2.1.1】 A = { x ∣ x ≥ 0 } \textbf{A}=\{x|x\ge 0\} A={x∣x≥0}, min A = 0 \text{min}\textbf{A}=0 minA=0,但是 max A \text{max}\textbf{A} maxA不存在。
【例2.1.2】 B = { x ∣ 0 ≤ x < 1 } \textbf{B}=\{x|0\le x < 1\} B={x∣0≤x<1}, min B = 0 \text{min}\textbf{B}=0 minB=0,但是 max B \text{max}\textbf{B} maxB不存在。
【证】假设 β ∈ B , β = max B \beta\in\textbf{B},\beta=\text{max}\textbf{B} β∈B,β=maxB,则 β ∈ [ 0 , 1 ) \beta\in[0,1) β∈[0,1),令 β ′ = 1 + β 2 ∈ [ 0 , 1 ) \beta'=\frac{1+\beta}{2}\in[0,1) β′=21+β∈[0,1)(取得很巧妙),则 β ′ ∈ B \beta'\in\textbf{B} β′∈B,但是 β ′ − β = 1 + β 2 − β = 1 − β 2 > 0 \beta'-\beta=\frac{1+\beta}{2}-\beta=\frac{1-\beta}{2}>0 β′−β=21+β−β=21−β>0,即 β ′ > β \beta'>\beta β′>β,与 β = max B \beta=\text{max}\textbf{B} β=maxB矛盾。
2.1.2 上确界与下确界
-
若 S ⊂ R , S ≠ ∅ \textbf{S}\subset\mathbb{R},\textbf{S}\ne\emptyset S⊂R,S=∅,若 ∃ M ∈ R \exists M\in\mathbb{R} ∃M∈R,使得 ∀ x ∈ S \forall x\in\textbf{S} ∀x∈S,有 x ≤ M x\le M x≤M,则称 M M M是 S \textbf{S} S的一个上界(上界不唯一,比 M M M大的都是上界),或称 S \textbf{S} S有上界。
设 U \textbf{U} U是 S \textbf{S} S上界的集合,则 U \textbf{U} U没有最大数,但 U \textbf{U} U必定有最小数(需证明,以后证明),记它为 β = sup S \beta=\sup \textbf{S} β=supS(supremum),称为 S \textbf{S} S的上确界。
β : { β 是上界,即 ∀ x ∈ S ,有 x ≤ β β 是最小上界,即 ∀ ξ > 0 , ∃ x ∈ S , 使得 x > β − ξ \beta:\left\{\begin{array}{l} \beta是上界,即\forall x \in \textbf{S},有x\le \beta \\ \beta是最小上界,即\forall \xi > 0,\exists x\in\textbf{S}, 使得x>\beta - \xi \end{array}\right. β:{β是上界,即∀x∈S,有x≤ββ是最小上界,即∀ξ>0,∃x∈S,使得x>β−ξ
【注】任何小于 β \beta β的数都不是集合 S \textbf{S} S的上界( β \beta β是最小上界的同义句),所以集合 S \textbf{S} S中一定存在不是上界的 x x x要大于任何小于 β \beta β的数 β − ξ \beta - \xi β−ξ,换句话说就是任何比 β \beta β小的数中存在着集合 S \textbf{S} S的元素,但是大于等于 β \beta β的数都是集合 S \textbf{S} S的上界,这样 β \beta β就成了一个“分界线”,比 β \beta β小的数 β − ξ \beta - \xi β−ξ中存在 S \textbf{S} S的元素,比 β \beta β大的数一定是 S \textbf{S} S的上界,那么 β \beta β子集就是上确界(自己理解的,欢迎数院大佬批评指正,下面是我画图理解的)

-
若 ∃ m ∈ S \exists m\in\textbf{S} ∃m∈S,使得 ∀ x ∈ S , x ≥ m \forall x\in\textbf{S},x\ge m ∀x∈S,x≥m,则称 m m m是 S \textbf{S} S的一个下界。
设 L \textbf{L} L是 S \textbf{S} S的集合,则 L \textbf{L} L没有最小数,但 L \textbf{L} L一定有最大数,记它为 α = inf S \alpha=\inf\textbf{S} α=infS(infimum),称为 S \textbf{S} S的下确界。
α : { α 是下界,即 ∀ x ∈ S ,有 x ≥ α α 是最大上界,即 ∀ ξ > 0 , ∃ x ∈ S , 使得 x < α + ξ \alpha:\left\{\begin{array}{l} \alpha是下界,即\forall x \in \textbf{S},有x\ge \alpha \\ \alpha是最大上界,即\forall \xi > 0,\exists x\in\textbf{S}, 使得x<\alpha + \xi \end{array}\right. α:{α是下界,即∀x∈S,有x≥αα是最大上界,即∀ξ>0,∃x∈S,使得x<α+ξ

相关文章:

【数学分析笔记】第2章第1节实数系的连续性(1)
2. 数列极限 2.1 实数系的连续性 人类对数系认识的历史: 人类最早对数系的认识是自然数集合 N \mathbb{N} N,自然数系对加法和乘法是封闭的(这里的封闭是指:若 m ∈ N , n ∈ N ⇒ m n ∈ N , m n ∈ N m\in\mathbb{N},n\in\ma…...

Speech Synthesis (LASC11062)
大纲 Module 1 – introductionModule 2 - unit selectionModule 3 - unit selection target cost functionsModule 4 - the databaseModule 5 - evaluationModule 6 - speech signal analysis & modellingModule 7 - Statistical Parametric Speech Synthesis (SPSS)Modu…...

拟合与插值|线性最小二乘拟合|非线性最小二乘拟合|一维插值|二维插值
挖掘数据背后的规律是数学建模的重要任务,拟合与插值是常用的分析方法 掌握拟合与插值的基本概念和方法熟悉Matlab相关程序实现能够从数据中挖掘数学规律 拟合问题的基本提法 拟合问题的概念 已知一组数据(以二维为例),即平面上n个点 ( x i , y i ) …...

《python语言程序设计》2018版第7章第05题几何:正n边形,一个正n边形的边都有同样的长度。角度同样 设计RegularPolygon类
结果和代码 这里只涉及一个办法 方法部分 def main():rX, rY eval(input("Enter regular polygon x and y axis:"))regular_num eval(input("Enter regular number: "))side_long eval(input("Enter side number: "))a exCode07.RegularPol…...

使用Virtio Driver实现一个计算阶乘的小程序——QEMU平台
目录 一、概述 二、代码部分 1、Virtio 前端 (1) User Space (2) Kernel Space 2、Virtio 后端 三、运行 QEMU Version:qemu-7.2.0 Linux Version:linux-5.4.239 一、概述 本篇文章的主要内容是使用Virtio前后端数据传输的机制实现一个计算阶乘的…...

【PyCharm】配置“清华镜像”地址
文章目录 前言一、清华镜像是什么?二、pip是什么?三、具体步骤1.复制镜像地址2.打开PyCharm,然后点击下图红框的选项3.在弹出的新窗口点击下图红框的选项进行添加4.在URL输入框中粘贴第一步复制的地址,名字可以不更改,…...

IO器件性能评估
整体逻辑:需要先了解到读写速率的差异,在明确使用场景。比如应用启动过程中的IO主要是属于随机读的io 评估逻辑: UFS 与 eMMC主要差别在io读写能力: 1,对比UFS、eMMC的规格书标注的io读写能力 ufs spec : sequentia…...

在js中判断对象是空对象的几种方法
使用 Object.keys() 方法 Object.keys() 方法返回对象自身的可枚举属性名称组成的数组。如果数组的长度为 0,那么对象是空的。 function isEmptyObject(obj) {return Object.keys(obj).length 0 && obj.constructor Object; }const obj1 {}; const obj2…...

【整理】后端接口设计和优化相关思路汇总
文章目录 明确的接口定义和文档化使用RESTful设计规范分页和过滤合理使用缓存限流与熔断机制安全性设计异步处理与后台任务接口参数校验(入参和出参)接口扩展性考虑核心接口,线程池隔离关键接口,日志打印接口功能单一性原则接口查…...

docker 部署 sql server
众所周知,sql server不好装,本人之前装了两次,这个数据库简直是恶心。 突然想到,用docker容器吧 果然可以 记得放开1433端口 还有 记得docker加速,不然拉不到镜像的最后工具还是要装的,这个就自己研究吧。 …...

微信云开发云存储 下载全部文件
一、安装 首先按照这个按照好依赖,打开cmd 安装 | 云开发 CloudBase - 一站式后端云服务 npm i -g cloudbase/cli 安装可能遇到的问题 ‘tcb‘ 不是内部或外部命令,也不是可运行的程序或批处理文件。-CSDN博客 二、登录 在cmd输入 tcb login 三、…...

1、巡线功能实现(7路数字循迹)
一、小车运行 1.PWM初始化函数 (pwm.c中编写) 包括四个轮子PWM通道使用的GPIO接口初始化、定时器初始化、PWM通道初始化。 void PWM_Init(uint16_t arr,uint16_t psc); 2.PWM占空比设置函数 (pwm.c中编写) 此函数调用了四个通道设置占空比的函数,作用是方便修改四…...

来了...腾讯内推的软件测试面试PDF 文档(共107页)
不多说,直接上干货(展示部分以腾讯面试纲要为例)完整版文末领取 通过大数据总结发现,其实软件测试岗的面试都是差不多的。常问的有下面这几块知识点: 全网首发-涵盖16个技术栈 第一部分,测试理论&#x…...

Android大脑--systemserver进程
用心坚持输出易读、有趣、有深度、高质量、体系化的技术文章,技术文章也可以有温度。 本文摘要 系统native进程的文章就先告一段落了,从这篇文章开始写Java层的文章,本文同样延续自述的方式来介绍systemserver进程,通过本文您将…...

python项目部署:Nginx和UWSGI认识
Nginx: HTTP服务器,反向代理,静态资源转发,负载均衡,SSL终端,缓存,高并发处理。 UWSGI: Python应用程序服务器,WSGI兼容,多进程管理,快速应用部署,多种协议支…...

【区块链+金融服务】农业大宗供应链线上融资平台 | FISCO BCOS应用案例
释放数据要素价值,FISCO BCOS 2024 应用案例征集 粮食贸易受季节性影响显著。每年的粮收季节,粮食收储企业会根据下游订单需求,从上游粮食贸易商或粮农手 里大量采购粮食,并分批销售给下游粮食加工企业(面粉厂、饲料厂…...

2025ICASSP Author Guidelines
Part I: General Information Procedure ICASSP 2025 论文提交与评审过程将与往届会议类似: 有意参加会议的作者需提交一份完整描述其创意和相关研究成果的文件,技术内容(包括图表和可能的参考文献)最多为4页&…...

Openstack 所需要的共享服务组件及核心组件
openstack 共享服务组件: 数据库服务(Database service):MariaDB及MongoDB 消息传输服务(messages queues):RabbitMQ 缓存(cache):Memcache 时间同步(time sync)&…...
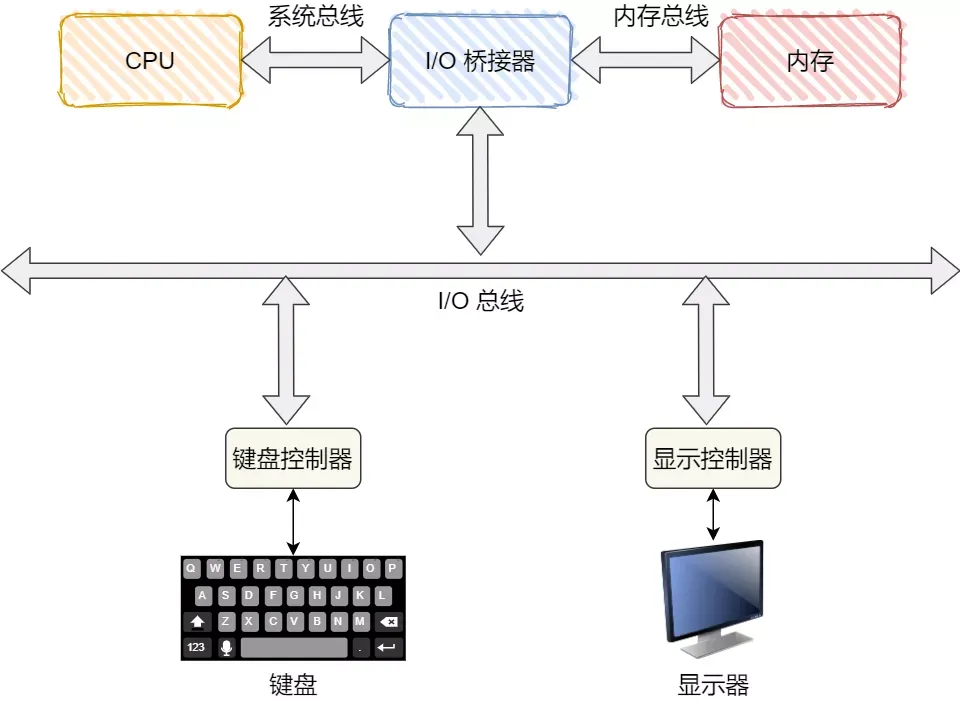
解密Linux中的通用块层:加速存储系统,提升系统性能
通用块层 通用块层是Linux中的一个重要组件,用于管理不同块设备的统一接口,减少不同块设备的差异带来的影响。它位于文件系统和磁盘驱动之间,类似于Java中的适配器模式,让我们无需关注底层实现,只需提供固定接口即可。…...
浅析国有商业银行人力资源数字化平台建设
近年来,在复杂的国际经济金融环境下,中国金融市场整体运行保持稳定。然而,随着国内金融机构改革的不断深化,国有商业银行全面完成股改上市,金融市场规模逐步扩大,体系日益完善,同时行业的竞争也…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...
