「字符串」前缀函数|KMP匹配:规范化next数组 / LeetCode 28(C++)
概述
为什么大家总觉得KMP难?难的根本就不是这个算法本身。
在互联网上你可以见到八十种KMP算法的next数组定义和模式串回滚策略,把一切都懂得特别混乱。很多时候初学者的难点根本不在于这个算法本身,而是它令人痛苦的百花齐放的定义。
有的next数组从0下标开始,有的从1开始;有的表示不包括本字符的前面部分的真前后缀,有的表示包括本字符的的前后缀,有的回滚+1,有的不+1,而他们却总是忽略这些异同,自顾自地讲KMP的匹配问题。初学者看到这直接傻了眼:随便挑两个视频或者文章,他们的定义和递推手段都不一样,让理解难度雪上加霜。
下面我们来先从字符串匹配讲起,想一想什么样的next数组定义才最适合这个算法本身。
LeetCode 28:
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。
示例 :
输入:haystack = "sadbutsad", needle = "sad" 输出:0 解释:"sad" 在下标 0 和 6 处匹配。 第一个匹配项的下标是 0 ,所以返回 0 。
*注意*: 接下来我们将称呼haystack为主串,needle为模式串。
思路
最普通的暴力算法总是在匹配失败后将主串指针i回滚到开始匹配的位置,模式串指针j回滚到0,然后在一轮for循环结束后执行i++操作来跳过这个匹配失败的位置。来看看Code。
class Solution {
public:int strStr(string haystack, string needle) {const int n=haystack.size();const int m=needle.size();for(int i=0;i<n;i++){if(haystack[i]==needle[0])for(int k=i,j=0;k<n;k++){if(haystack[k]==needle[j])j++;else break;if(j==m)return i;}}return -1;}
};来想一想:都回滚j了,为什么还回滚i?难道就因为有一个字符匹配失败了就放弃前面所有的努力吗?
至少在最后的失败字符之前,我们匹配成功了。这意味着:
模式串为pattern,主串为mainj
pattern[j] a b c a b f g√ √ √ √ √ ×main[i] a b c a b k v q x ti至少在'f'字符与'k'字符对比之前,我们的匹配成功了。
这意味着,main函数的此前部分和pattern的此前部分一一对应,我们称之为str1。
这时候的一个独到之处就是:
在这段主串和模式串共同的[开头,失配位置)的子串str1中,匹配失败之前的任意位置,从这个位置开始,一直到匹配失败的位置之前他们都相同,这部分[任意位置,失配位置)的子串我们称为str2。
那我们可以有一个特殊的回滚模式串指针j的手段:不回滚到最开头,而是回滚到模式串的某个位置,在这个位置以前的部分模式串[开头,某位置)称为str3,它与str2相同。
结合例子感受一下:
模式串为pattern,主串为main┌str3┐ j<-------j
pattern[j] |a b c a b |f g| └str2┘| |√ √ √ √ √ || ┌str2┑|main[i] |a b c a b |k v q x t└----str1------┘i这样看还是不够清晰,我们把j的移动形象理解成模式串的移动。
模式串为pattern,主串为main┌str3┐ j<-------j
pattern[j] a b c a b f g└str2┘ √ √┌str2┑main[i] a b c a b k v q x t└----str1-----┘ i也就是说:在j倒退回某个位置后,这位置之前的模式串部分和主串部分是天生匹配的。
接下来我会用前后缀的语言代替“某某部分”:
//这是对前后缀的解释,如果你了解,可以跳过
对于一个字符串
begin enda b a c d x f a c a d----> ---->前缀 后缀 //*注意*:前后缀的字符顺序都是从前向后
前缀是从[begin,x]的任意子字符串 真前缀的x不等于end
后缀是从 [x,end] 的任意子字符串 真后缀的x不等于begin归纳一下:
当匹配到主串i位置和模式串j位置,匹配失败时:
str2既是主串的[0,i)子串的一个后缀,又是模式串的[0,j)子字符串的一个后缀。
str3则是模式串中[0,j)子串的某个前缀,这个前缀与str2这个后缀相等。
因此,模式串中的str3能与模式串中的str2匹配,就意味着模式串中的str3与主串中的str2与是天生匹配的。
形象理解:
str3==str2
pattern -str3------str2-√√√√√√√√√√√√√√√×
main -----------str2-↓
pattern -str3------str2-√√√√√?
main -----------str2-那按理来说,这是一个模式串的自匹配问题:对于模式串的每个位置j,都有[0,j)子串,都要找到他们的最长相同真前后缀。
因此问题就转化成了:
枚举模式串的每个下标j,求成它的[0,j)子字符串的最长相同真前后缀,这样,当在任意位置匹配失败时,都可以知道j的回滚位置了,而i从不回滚。
核心概念:前缀函数
网络上各种奇异搞笑的next数组定义的根本来源是他们没搞懂前缀函数和next数组的区别。
前缀函数是一个独立的算法函数概念,next数组只是它针对于KMP算法的特化版本。
1.前缀函数
它写作π[i]或PM[i]。
定义:
给定一个长度为n的字符串,其前缀函数被定义为一个长度为n的数组π[n](或:PM[n])。 其中π[i]的意义是:字符串的[0,i]子字符串的最长相同真前后缀。

故有:
j 0 1 2 3 4 5 6
string str[j] a b c a b c dπ[j] 0 0 0 1 2 3 0这是标准的前缀函数定义,他长度就是n,下标起始位置就是0,其他的任何一种next数组都是他的特化版本。
*注意*:我通常使用j来作为next数组和模式串的索引。
2.next数组
在KMP匹配算法中,π数组变成了next数组,有如下几种方案:
1.考研版本
①模式串、主串和next数组下标统一从1开始计数。[j]表示第j个字符处,而不是索引0代表第1个字符。next[0]值为-1。
②next[j]表示原字符串{s[1]...s[j-1]}的最长相同真前后缀长度,它记录在了next[j]。next[j]的值不包括第j个字符。
③回滚代码:j=next[j]+1。
例如上文的"abcabcd",如果当j=7失配时,next[j]==3,那么j会从4开始继续匹配,跳过了123。
j 0 1 2 3 4 5 6 7
string str[j] n a b c a b c dnext[j] -1 0 0 0 0 1 2 3
//n通常储存字符串的长度信息。*注意*:你还会见到next[0]=0,且next数组整体+1的版本,它是另一个考研版本,只是将回滚代码的+1操作融入了next数组中,回滚代码:j=next[j],此处不再赘述。
2.竞赛版本
事实上,在竞赛或者各大算法平台,字符串下标仍然从0开始,我们要为这个原则服务。
①字符串下标仍然从0开始,但我们仍然期望next数组下标从1开始。即主串与模式串从0开始,next数组从1开始,next数组长度比模式串大1,后续你会发现这样做的好处。
②next[j]表示原字符串*前j个字符*的最长相同真前后缀长度,它记录在了next[j],这里发生了错位。(next[0]=0,这样当j=0时执行回滚不会发生溢出,next[1]=0,第一个字符没有真先后缀)。
③回滚代码:j=next[j]。next数组错位的目的就是避免回滚代码发生+1-1的问题,这样能有效规避溢出。
例如上文的"abcabcd" ,如果当j=6失配时,next[j]==3,那么j会从3开始继续匹配,跳过了012。
即:j在某处失配时,它前面有j个字符,且这j个字符最长相同前后缀长度len储存在了next[j],可以快速访问next[j]得到j的回滚位置,回滚后恰好跳过len个字符。(我们总是期望在一轮for循环后j指向一个有待下一轮循环商榷的位置,不论是j++还是j=next[j],都是这样的。)
j 0 1 2 3 4 5 6 7
string str[j] a b c a b c d \0next[j] 0 0 0 1 2 3 0 算法过程
*注意*:我们会以竞赛版本的KMP进行讲解。它稍微更改就可以变成考研版。(比如insert函数)
构建next数组
构建next数组才是KMP本身具有难度的地方。
推论:字符串增加一个字符,它的最长相同真前后缀至多+1。这个不起眼的推论是构建的核心。
但是我们可以将其总结为3点:
①next[0]=0,next[1]=0,这两个直接无视。随后发生for循环int i=1,j=0。
i向前探索;j即用于为next[i+1]赋值,又作为下标索引与向前探索的i遥相呼应:[0,j]与[i-j,i]匹配。
因此j同时代表着:[0,i]的公共前后缀长度数值,也是与i这个前方洗标呼应的后方下标。
记得我们的定义是:next[j]表示原字符串*前j个字符*的最长相同真前后缀长度,i+1这个值才是[0,i]字符串的字符个数,因此j为next[i+1]赋值。
②当pattern[i]!=pattern[j],即位置i与位置j字符不匹配,通过while循环回滚j,如果仍失配,继续回滚,一直到j==0。
这一点是KMP的精髓所在:我们一边构建next数组,一边利用next数组回滚j。
这听起来很不可思议,但是注意:next数组是从前向后构建的,而回滚是向前的。这说明:我们在利用已经构建起的next数组进行回滚,而不会发生某种奇怪的冲突。
但是为什么用next数组回滚j呢?还记得next数组是干什么用的吗?它就是指示:当失配时,请从这里再试一试。不一定非要模式串与主串匹配才有失配,模式串自匹配时前缀不等于后缀也叫失配。我们回滚j就是期望将j回滚到可能与pattern[i]匹配的位置。
如果一直到j==0还失败,那就意味着不存在相同前后缀,那么为next[i+1]=j(即赋0值也是合理的了)
③判断pattern[i]是否等于pattern[j]。
如果因为j与i成功匹配而脱离while循环,那么j++,因为我们的最长相同前后缀+1。
void get_next(string&pattern,vector<int>&next){next[0]=0,next[1]=0;const int m=pattern.size();for(int i=1,j=0;i<m;i++){while(j&&pattern[j]!=pattern[i])j=next[j];if(pattern[j]==pattern[i])j++;next[i+1]=j;//赋值发生在j++之后,所以此处不用+1}}匹配过程
匹配过程与构建过程极其类似。
主要是以下三点:
①当main[i]!=pattern[j],即在此处失配时,通过while循环回滚j,如果仍失配,继续回滚,一直到j==0。
②跳出while后判断main[i]是否等于pattern[j]。
由于脱离while要么是两者相等,要么不相等但j==0,那么:
if为真意味着:两者匹配成功,j++,i++。(两者在一轮循环后分别指向有待下一轮循环商榷的位置。)
if为假意味着:这一步就是判断出现j等于0且仍无法匹配的状况,那么认为这个i终究无法匹配,j停滞在0,随后放弃i的当前位置,i自增。
③判断j==m,这意味着完全匹配,返回i-m+1。(注意这里有个+1的细节:一轮for循环结束之前i++还未发生)
for(int i=0,j=0;i<n;i++){while(j&&main[i]!=pattern[j])j=next[j];if(main[i]==pattern[j])j++;if(j==m)return i-m+1;
}
return -1;复杂度
时间复杂度:O(n+m)
空间复杂度:O(m)
n:主串长度
m:模式串长度
Code
class Solution {
public:void get_next(string&pattern,vector<int>&next){const int m=pattern.size();for(int i=1,j=0;i<m;i++){while(j&&pattern[j]!=pattern[i])j=next[j];if(pattern[j]==pattern[i])j++;next[i+1]=j;}}int strStr(string haystack, string needle) {const int n=haystack.size(),m=needle.size();vector<int>next(m+1,0);get_next(needle,next);for(int i=0,j=0;i<n;i++){while(j&&haystack[i]!=needle[j])j=next[j];if(haystack[i]==needle[j])j++;if(j==m)return i-m+1;}return -1;}
};(如果你充分理解了本文,就会发现代码竟然如此直观) 。
相关文章:

「字符串」前缀函数|KMP匹配:规范化next数组 / LeetCode 28(C++)
概述 为什么大家总觉得KMP难?难的根本就不是这个算法本身。 在互联网上你可以见到八十种KMP算法的next数组定义和模式串回滚策略,把一切都懂得特别混乱。很多时候初学者的难点根本不在于这个算法本身,而是它令人痛苦的百花齐放的定义。 有…...

python人工智能002:jupyter基本使用
小知识:将jupyter修改为中文,修改用户变量, 注意是用户变量,不是系统变量 新增用户变量 变量名:LANG 变量值:zh_CN.UTF8 然后重启jupyter 上一章的软件安装完成之后,就可以创建文件夹来学习写…...

Linux使用 firewalld管理防火墙命令
Linux 发行版中使用的动态防火墙管理工具。使用 firewalld,你可以查看防火墙状态、当前配置的规则以及开放的端口。以下是一些常用的 firewalld 命令来管理和查看防火墙状态及端口配置。 1. 查看防火墙状态 检查 firewalld 是否正在运行 sudo systemctl status f…...

二叉树(三)
一、二叉树的遍历 二叉树遍历是按照某种特定的规则,依次对二叉树中的结点进行相应的操作,并且每个结点只操作一次。 1.前序遍历(先根遍历) 前序遍历(Preorder Traversal也叫先序遍历)——根、左子树、右…...
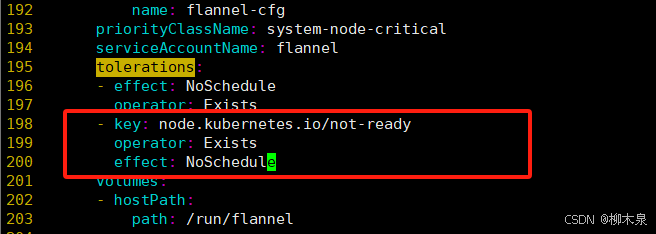
05--kubernetes组件与安装
前言:终于写到kubernetes(k8s),容器编排工具不止k8s一个,它的优势在于搭建集群,也是传统运维和云计算运维的第一道门槛,这里会列出两种安装方式,详细步骤会在下文列出,文…...

EmguCV学习笔记 VB.Net和C# 下的OpenCv开发 C# 目录
版权声明:本文为博主原创文章,转载请在显著位置标明本文出处以及作者网名,未经作者允许不得用于商业目的。 EmguCV是一个基于OpenCV的开源免费的跨平台计算机视觉库,它向C#和VB.NET开发者提供了OpenCV库的大部分功能。 教程VB.net版本请访问…...

探索TensorFlow:深度学习的未来
标题:探索TensorFlow:深度学习的未来 在当今快速发展的人工智能领域,TensorFlow无疑是最耀眼的明珠之一。TensorFlow是由Google Brain团队开发的一个开源机器学习框架,它以其强大的灵活性、易用性和高效的性能,迅速成…...

探索地理空间分析的新世界:Geopandas的魔力
文章目录 探索地理空间分析的新世界:Geopandas的魔力背景:为何选择Geopandas?这个库是什么?如何安装这个库?五个简单的库函数使用方法场景应用:Geopandas在实际工作中的应用常见bug及解决方案总结 探索地理…...

如何为网站申请免费SSL证书?
一、准备阶段 确定证书类型: 对于大多数个人博客和小型企业网站,DV(域名验证)SSL证书已足够使用,因为它仅验证域名所有权,成本较低且验证快速。准备域名: 确保你拥有一个有效的域名,…...

Java项目集成RocketMQ
文章目录 1.调整MQ的配置1.进入bin目录2.关闭broker和namesrv3.查看进程确认关闭4.编辑配置文件broker.conf,配置brokerIP15.开放端口109116.重新启动1.进入bin目录2.启动mqnamesrv和mqbroker1.启动 NameServer 并将输出重定向到 mqnamesrv.log2.**启动 Broker 并将…...

如何将 Bamboo agent 能力迁移到极狐GitLab tag 上?
极狐GitLab 是 GitLab 在中国的发行版,专门面向中国程序员和企业提供企业级一体化 DevOps 平台,用来帮助用户实现需求管理、源代码托管、CI/CD、安全合规,而且所有的操作都是在一个平台上进行,省事省心省钱。可以一键安装极狐GitL…...

正则表达式入门:Python ‘ re ‘ 模块详解
正则表达式(Regular Expression,简称 re)是一种强大而灵活的工具,广泛用于字符串匹配、替换和分割等操作,尤其在处理网页爬虫数据时非常有用。Python 提供了 " re " 模块来支持正则表达式的使用,…...
pc网站支付)
thinkphp8.0+aliapy(支付宝)pc网站支付
环境:宝塔-centOS8.5,php8.3 第一步:安装alipay v3版本的安装依赖包; composer require alipaysdk/openapi:dev第二步:根据官方文档,把支付相关的类引用进来; <?php declare (strict_types 1);namespace app\p…...

高速信号的眼图、加重、均衡
目录 高速信号的眼图、加重、均衡眼图加重均衡线性均衡器CTLE判决反馈均衡器DFE 高速信号的眼图、加重、均衡 眼图 通常用示波器观察接收信号波形的眼图来分析码间串扰和噪声对系统性能的影响,从而估计系统优劣程度,因而眼图分析是高速互连系统信号完整…...
2024年PMP考前冲刺必背的学习笔记,整理好给你!
项目的四大特点:临时性、独特性、变革驱动性和创造商业价值。 项目管理:将知识、技能、工具与技术应用于项目活动,以满足项目的要求 Pestle:P政治,E经济,S社会,T技术,L法律,E环境 …...

增加服务器带宽可以提高资源加载速度吗?
答案是可以的 ,增加服务器带宽通常能够提高资源加速速度。带宽是服务器与互联网之间传输数据的速率,它决定了在单位时间内可以传输的数据量。以下是增加带宽如何提高资源加速速度的几个方面: 1.更快的数据传输:带宽增加后…...

汽车EDI: NAVISTAR EDI对接
Navistar International Corporation 是一家美国商用车辆制造公司,总部位于伊利诺伊州的Lisle。公司以生产中型和重型卡车、公共汽车、柴油发动机和底盘闻名,其产品广泛应用于运输、建筑、和农业等行业。Navistar 的历史可以追溯到1831年,由国…...
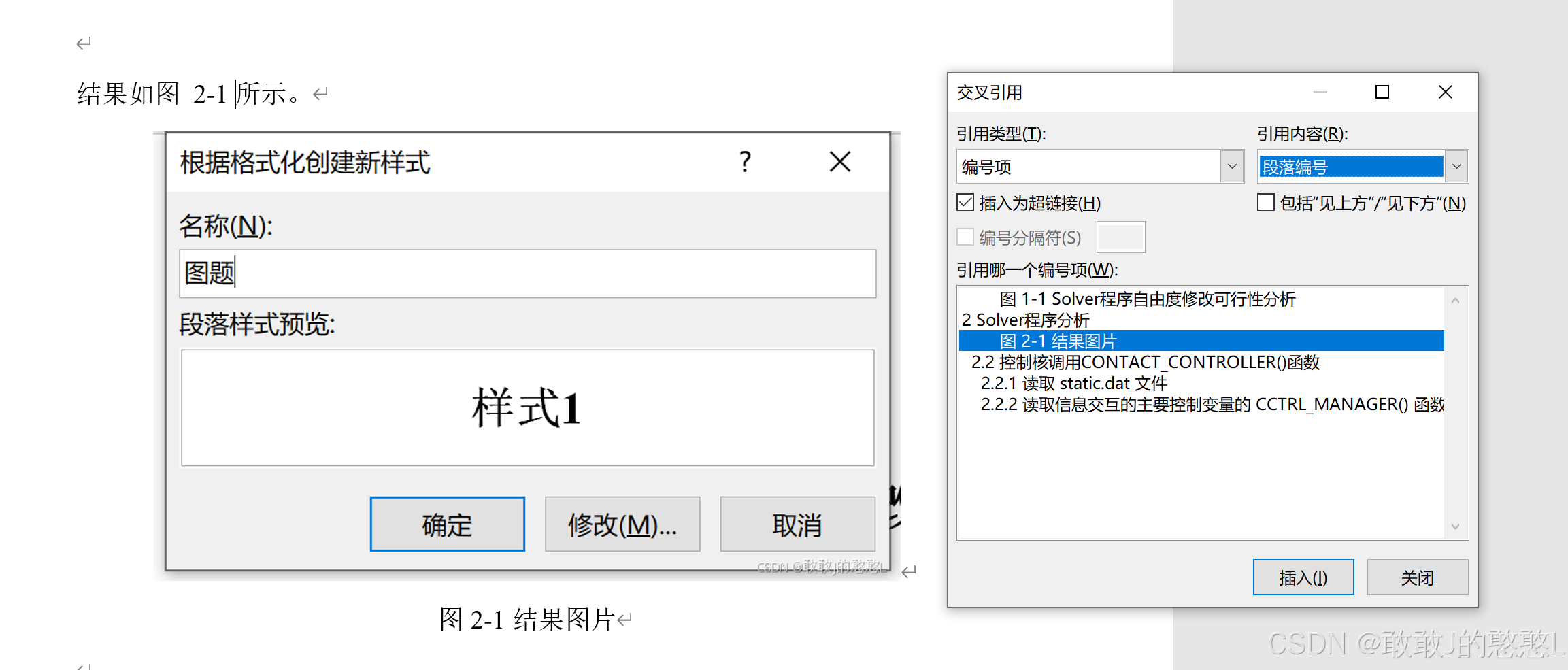
【Word多级标题完整设置】设置各级标题样式将多级列表链接到各级标题样式中
Word多级标题完整设置 一、设置各级标题样式主标题样式设置中英文字体、字形以及字号设置段落设置(缩进、间距和行距) 一级标题样式设置中英文字体、字形以及字号设置段落设置(缩进、间距和行距) 二级标题样式设置中英文字体、字形…...

不同分辨率下vue页面的高度自适应
1. 使用视口单位 .element { height: 100vh; /* 使得元素高度等于视口高度的100% */ /* 可以减去一部分高度以适应页眉或页脚 */ height: calc(100vh - 100px); } 2. 使用百分比(%)高度 .parent { height: 100vh; /* 父元素高度等于视口高度 */…...
“野生钢铁侠 “ 稚晖君一连亮出5 款智元人形机器人,地表最强!
打麻将、拆快递、纽扣穿针,还能做 30KG 重物提拉! 沉寂一年,稚晖君带着他的二代机器人全家桶重磅回归,秀出的各种新技能令人眼前一亮。 智东西 8 月 18 日报道,今日," 野生钢铁侠 " 稚晖君一连亮…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...
