蚁群算法原理与实战(Python、MATLAB、C++)
蚁群算法
1.蚁群算法来源
蚁群算法(Ant Colony Optimization,简称ACO)是一种模拟自然界中蚂蚁寻找食物路径行为的优化算法,主要用于解决组合优化问题。它的灵感来源于意大利学者Marco Dorigo在1992年提出的蚂蚁系统模型。

蚁群算法的灵感来源于自然界中蚂蚁寻找食物的行为。蚂蚁在寻找食物的过程中会释放一种称为信息素的化学物质,这种物质会在蚂蚁走过的路径上留下痕迹,后续的蚂蚁会根据这些信息素的浓度来选择路径,从而形成一条从蚁巢到食物源的最短路径。蚂蚁觅食的过程是一个正反馈的过程,该路段经过的蚂蚁越多,信息素留下的就越多,浓度越高,更多的蚂蚁都会选择这个路段。
这种行为模式启发了科学家们设计出蚁群算法,用于解决复杂的优化问题。
2.蚁群算法基本原理

蚁群算法的基本原理可以概括为以下几个步骤:
(1)初始化:设定每个解(相当于蚂蚁可能行走的路径)的信息素初始值,通常设置为一个较小的正数。
(2)蚂蚁构建解:每只蚂蚁根据当前的信息素浓度和启发式信息(如距离的倒数)来选择下一步要走的路径。这个过程是概率性的,信息素浓度越高,被选中的概率越大。
(3)信息素更新:一轮搜索结束后,根据蚂蚁找到的解的质量来更新信息素。通常情况下,较优的解对应的路径上的信息素会被加强,而较差解对应的信息素则会减少或蒸发。
(4)循环迭代:重复上述过程,直到满足停止条件(如达到最大迭代次数或解的质量不再明显提高)。
通过这样的机制,蚁群算法能够在解空间中逐渐逼近最优解。需要注意的是,蚁群算法是一种随机优化算法,每次运行可能会得到不同的结果,但多次运行后往往能够找到接近最优的解。
数学原理:

3.蚁群算法的应用
蚁群算法的应用非常广泛,包括旅行商问题(TSP)、图着色问题、网络路由优化、调度问题等。它特别适合于解决大规模的、复杂的优化问题,尤其是那些难以用传统数学方法求解的问题。
下面简单介绍一些经典的应用:
(1)旅行商问题(TSP):最初被用于解决TSP问题,即在给定一组城市中找到最短的巡回路径。

(2)物流和交通:用于优化物流配送路径、车辆路径规划和交通信号控制等问题。
**(3)网络路由:**在计算机网络和通信网络中,用于动态路由选择以提高网络效率。
**(4)生产调度:**在制造业中,用于优化生产计划和调度,减少生产成本和时间。
**(5)图像处理:**用于图像分割、边缘检测等图像处理任务。
(6)图着色问题:

4.蚁群算法解决TSP问题
旅行商问题(Traveling saleman problem, TSP)是物流配送的典型问题,其求解有十分重要的理论和现实意义。
旅行商问题传统的解决方法都是遗传算法,但是遗传算法的收敛速度慢,具有一定的缺陷。
在求解TSP蚁群算法中,每只蚂蚁相互独立,用于构造不同的路线,蚂蚁之间通过信息素进行交流,合作求解。
动图展示TSP问题求解过程:

下面介绍一下具体流程:
(1)初始化参数:epochs表示迭代次数,ants表示蚂蚁数量,alpha和beta是信息素重要程度的参数,rho是信息素挥发速度,Q是信息素强度常数。
(2)计算城市之间的距离矩阵:使用numpy的linalg.norm函数计算每对城市之间的欧几里得距离,并将结果存储在Distance矩阵中。
(3)初始化信息素矩阵Tau:将所有元素设置为1.0。
(4)初始化每只蚂蚁的路线图Route:创建一个ants x cities的零矩阵,表示每只蚂蚁访问过的城市。
(5)进行迭代:对于每次迭代,首先为每只蚂蚁随机选择一个起始城市,然后根据概率选择下一个要访问的城市。概率由信息素浓度和启发式信息共同决定。
(6)计算每只蚂蚁的总距离:遍历每只蚂蚁的路线,累加经过的城市之间的距离。
(7)更新最优解:如果当前迭代中找到了一条更短的路径,就更新最优距离和最优路线。
(8)更新信息素:根据蚂蚁走过的路径,更新信息素矩阵Tau。
(9)输出结果:打印出找到的最短路径和对应的距离。
程序中各符号说明如下表格:
| 变量/矩阵名称 | 维度 | 描述 |
|---|---|---|
| position | (cities, 2) | 城市坐标数组,每行代表一个城市的x和y坐标。 |
| Distance | (cities, cities) | 城市之间的距离矩阵,存储每两个城市之间的欧几里得距离。 |
| Eta | (cities, cities) | 启发式信息矩阵,是Distance矩阵的倒数,用于指导蚂蚁选择路径。 |
| Tau | (cities, cities) | 信息素矩阵,表示在每两个城市之间的路径上的信息素浓度。 |
| Route | (ants, cities) | 蚂蚁路径矩阵,存储每一只蚂蚁在当前迭代中的路径。 |
| best_distance | 1 | 变量,存储迄今为止找到的最短路径的长度。 |
| best_route | (cities,) | 数组,存储迄今为止找到的最短路径的城市顺序。 |
| epochs | 1 | 算法运行的迭代次数。 |
| ants | 1 | 蚁群中蚂蚁的数量。 |
| alpha | 1 | 信息素重要性的影响因子。 |
| beta | 1 | 启发式信息重要性的影响因子。 |
| rho | 1 | 信息素蒸发率。 |
| Q | 1 | 信息素强度,用于在每次迭代后更新信息素矩阵。 |
最终结果展示:


完整python代码如下:
import numpy as np
import random# 城市坐标
x = np.array([51, 27, 56, 21, 4, 6, 58, 71, 54, 40, 94, 18, 89, 33, 12, 25, 24, 58, 71, 94, 17, 38, 13, 82, 12, 58, 45, 11, 47, 4])
y = np.array([14, 81, 67, 92, 64, 19, 98, 18, 62, 69, 30, 54, 10, 46, 34, 18, 42, 69, 61, 78, 16, 40, 10, 7, 32, 17, 21, 26, 35, 90])
position = np.column_stack((x, y))epochs = 50
ants = 50
alpha = 1.4
beta = 2.2
rho = 0.15
Q = 10**6
cities = position.shape[0]# 城市之间的距离矩阵
Distance = np.ones((cities, cities))
for i in range(cities):for j in range(cities):if i != j:Distance[i, j] = np.linalg.norm(position[i] - position[j])else:Distance[i, j] = np.finfo(float).epsEta = 1.0 / Distance
Tau = np.ones((cities, cities))# 每只蚂蚁的路线图
Route = np.zeros((ants, cities))
best_distance = np.inf
best_route = np.zeros(cities)for epoch in range(epochs):# 为每只蚂蚁随机选择一个唯一的起始城市start_cities = np.random.permutation(cities).tolist()for i in range(ants):Route[i, 0] = start_cities[i % cities]for j in range(1, cities):for i in range(ants):Visited = Route[i, :j]NoVisited = np.setdiff1d(np.arange(cities), Visited)P = np.zeros(len(NoVisited))for k in range(len(NoVisited)):P[k] = (Tau[int(Visited[-1]), int(NoVisited[k])] ** alpha) * (Eta[int(Visited[-1]), int(NoVisited[k])] ** beta)P = P / P.sum()Pcum = np.cumsum(P)select = np.where(Pcum >= random.random())[0][0]to_visit = NoVisited[select]Route[i, j] = to_visitDistance_epoch = np.zeros(ants)for i in range(ants):R = Route[i, :]for j in range(cities - 1):Distance_epoch[i] += Distance[int(R[j]), int(R[j + 1])]Distance_epoch[i] += Distance[int(R[0]), int(R[-1])]best_distance_epoch = np.min(Distance_epoch)best_index_epoch = np.argmin(Distance_epoch)if best_distance_epoch < best_distance:best_distance = best_distance_epochbest_route = Route[best_index_epoch, :]Delta_Tau = np.zeros((cities, cities))for i in range(ants):for j in range(cities - 1):Delta_Tau[int(Route[i, j]), int(Route[i, j + 1])] += Q / Distance_epoch[i]Delta_Tau[int(Route[i, 0]), int(Route[i, -1])] += Q / Distance_epoch[i]Tau = (1 - rho) * Tau + Delta_Tauprint("最短路径:", best_route)
print("最短距离:", best_distance)
MATLAB代码如下:
动图显示路径部分
function DrawRoute(C, R)
N = length(R);
scatter(C(:, 1), C(:, 2));
hold on
plot([C(R(1), 1), C(R(N), 1)], [C(R(1), 2), C(R(N), 2)], 'g');
for ii = 2: Nhold onplot([C(R(ii - 1), 1), C(R(ii), 1)], [C(R(ii - 1), 2), C(R(ii), 2)], 'g');pause(0.1)frame = getframe(gcf);imind = frame2im(frame);[imind, cm] = rgb2ind(imind, 256);if ii == 2imwrite(imind, cm, 'test.gif', 'gif', 'Loopcount', inf, 'DelayTime', 1e-4);elseimwrite(imind, cm, 'test.gif', 'gif', 'WriteMode', 'append', 'DelayTime', 1e-4);end
end
title('旅行商规划');
蚁群算法部分:
clear;
clc;
x=[51 27 56 21 4 6 58 71 54 40 94 18 89 33 12 25 24 58 71 94 17 38 13 82 12 58 45 11 47 4]';
y=[14 81 67 92 64 19 98 18 62 69 30 54 10 46 34 18 42 69 61 78 16 40 10 7 32 17 21 26 35 90]';
position = 100 * randn(40, 2);
% position = [x, y];
epochs = 50;
ants = 50;
alpha = 1.4;
beta = 2.2;
rho = 0.15;Q = 10^6;
cities = size(position, 1);
% 城市之间的距离矩阵
Distance = ones(cities, cities);
for i = 1: citiesfor j = 1: citiesif i ~= jDistance(i, j) = ((position(i, 1) - position(j, 1))^2 + (position(i, 2) - position(j, 2))^2)^0.5;elseDistance(i, j) = eps;endDistance(j, i) = Distance(i, j);end
end
Eta = 1./Distance;
Tau = ones(cities, cities);
% 每只蚂蚁的路线图
Route = zeros(ants, cities);
epoch = 1;
% 记录每回合最优城市
R_best = zeros(epochs, cities);
L_best = inf .* ones(epochs, 1);
L_ave = zeros(epochs, 1);
% 开始迭代
while epoch <= epochs% 随机位置RandPos = [];for i = 1: ceil(ants / cities)RandPos = [RandPos, randperm(cities)];endRoute(:, 1) = (RandPos(1, 1:ants))';for j = 2:citiesfor i = 1: antsVisited = Route(i, 1:j-1);NoVisited = zeros(1, (cities - j + 1));P = NoVisited;num = 1;for k = 1: citiesif length(find(Visited == k)) == 0NoVisited(num) = k;num = num + 1;endendfor k = 1: length(NoVisited)P(k) = (Tau(Visited(end), NoVisited(k))^alpha) * (Eta(Visited(end), NoVisited(k))^beta);endP = P / sum(P);Pcum = cumsum(P);select = find(Pcum >= rand);to_visit = NoVisited(select(1));Route(i, j) = to_visit;endendif epoch >= 2Route(1, :) = R_best(epoch - 1, :);endDistance_epoch = zeros(ants, 1);for i = 1: antsR = Route(i, :);for j = 1: cities - 1Distance_epoch(i) = Distance_epoch(i) + Distance(R(j), R(j + 1));endDistance_epoch(i) = Distance_epoch(i) + Distance(R(1), R(cities));endL_best(epoch) = min(Distance_epoch);pos = find(Distance_epoch == L_best(epoch));R_best(epoch, :) = Route(pos(1), :);L_ave(epoch) = mean(Distance_epoch);epoch = epoch + 1;Delta_Tau = zeros(cities, cities);for i = 1: antsfor j = 1: (cities - 1)Delta_Tau(Route(i, j), Route(i, j + 1)) = Delta_Tau(Route(i, j), Route(i, j + 1)) + Q / Distance_epoch(i);endDelta_Tau(Route(i, 1), Route(i, cities)) = Delta_Tau(Route(i, 1), Route(i, cities)) + Q / Distance_epoch(i);endTau = (1 - rho) .* Tau + Delta_Tau;Route = zeros(ants, cities);
end
%% 结果展示
Pos = find(L_best == min(L_best));
Short_Route = R_best(Pos(1), :);
Short_Length = L_best(Pos(1), :);
figure
% subplot(121);
DrawRoute(position, Short_Route);
% subplot(122);
% plot(L_best);
% hold on
% plot(L_ave, 'r');
% title('平均距离和最短距离');
蚁群算法解决TSP问题(c++)
#include<iostream>
#include<stdio.h>
#include<string>
#include<string.h>
#include<cmath>
#include<ctime>
#include<stdlib.h>
using namespace std;
int seed=(int)time(0);//产生随机种子
int CityPos[30][2]= {{87,7},{91,38},{83,46},{71,44},{64,60},{68,58},{83,69},{87,76},{74,78},{71,71},{58,69},{54,62},{51,67},{37,84},{41,94},{2,99},{7,64},{22,60},{25,62},{18,54},{4,50},{13,40},{18,40},{24,42},{25,38},{41,26},{45,21},{44,35},{58,35},{62,32}};
#define CITY_NUM 30//城市数量
#define ANT_NUM 30//蚁群数量
#define TMAC 10000//迭代最大次数
#define ROU 0.5//误差大小
#define ALPHA 1//信息素重要程度的参数
#define BETA 4//启发式因子重要程度的参数
#define Q 100//信息素残留参数
#define maxn 100
#define inf 0x3f3f3f3f
double dis[maxn][maxn];//距离矩阵
double info[maxn][maxn];//信息素矩阵
bool vis[CITY_NUM][CITY_NUM];//标记矩阵//返回指定范围内的随机整数
int rnd(int low,int upper)
{return low+(upper-low)*rand()/(RAND_MAX+1);
}//返回指定范围内的随机浮点数
double rnd(double low,double upper)
{double temp=rand()/((double)RAND_MAX+1.0);return low+temp*(upper-low);
}struct Ant
{int path[CITY_NUM];//保存蚂蚁走的路径double length;//路径总长度bool vis[CITY_NUM];//标记走过的城市int cur_cityno;//当前城市int moved_cnt;//已走城市数量//初始化void Init(){memset(vis,false,sizeof(vis));length=0;cur_cityno=rnd(0,CITY_NUM);path[0]=cur_cityno;vis[cur_cityno]=true;moved_cnt=1;}//选择下一个城市int Choose(){int select_city=-1;//所选城市编号double sum=0;double prob[CITY_NUM];//保存每个城市被选中的概率for(int i=0; i<CITY_NUM; i++){if(!vis[i]){prob[i]=pow(info[cur_cityno][i],ALPHA)*pow(1.0/dis[cur_cityno][i], BETA);sum=sum+prob[i];}else{prob[i]=0;}}//进行轮盘选择double temp=0;if(sum>0)//总的信息素大于0{temp=rnd(0.0,sum);for(int i=0; i<CITY_NUM; i++){if(!vis[i]){temp=temp-prob[i];if(temp<0.0){select_city=i;break;}}}}else //信息素太少就随便找个没走过的城市{for(int i=0; i<CITY_NUM; i++){if(!vis[i]){select_city=i;break;}}}return select_city;}//蚂蚁的移动void Move(){int nex_cityno=Choose();path[moved_cnt]=nex_cityno;vis[nex_cityno]=true;length=length+dis[cur_cityno][nex_cityno];cur_cityno=nex_cityno;moved_cnt++;}//蚂蚁进行一次迭代void Search(){Init();while(moved_cnt<CITY_NUM){Move();}//回到原来的城市length=length+dis[path[CITY_NUM-1]][path[0]];}
};struct TSP
{Ant ants[ANT_NUM];//定义蚁群Ant ant_best;//最优路径蚂蚁void Init(){//初始化为最大值ant_best.length = inf;//计算两两城市间距离for (int i = 0; i < CITY_NUM; i++){for (int j = 0; j < CITY_NUM; j++){info[i][j]=1.0;double temp1=CityPos[j][0]-CityPos[i][0];double temp2=CityPos[j][1]-CityPos[i][1];dis[i][j] = sqrt(temp1*temp1+temp2*temp2);}}}//更新信息素void UpdateInfo(){double temp_info[CITY_NUM][CITY_NUM];memset(temp_info,0,sizeof(temp_info));int u,v;for(int i=0; i<ANT_NUM; i++) //遍历每一只蚂蚁{for(int j=1; j<CITY_NUM; j++){u=ants[i].path[j-1];v=ants[i].path[j];temp_info[u][v]=temp_info[u][v]+Q/ants[i].length;temp_info[v][u]=temp_info[u][v];}//最后城市和开始城市之间的信息素u=ants[i].path[0];temp_info[u][v]=temp_info[u][v]+Q/ants[i].length;temp_info[v][u]=temp_info[u][v];}for(int i=0; i<CITY_NUM; i++){for(int j=0; j<CITY_NUM; j++){info[i][j]=info[i][j]*ROU+temp_info[i][j];}}}void Search(){//迭代TMAC次for(int i=0; i<TMAC; i++){//所有蚂蚁都进行一次遍历for(int j=0; j<ANT_NUM; j++){ants[j].Search();}//保存所有蚂蚁遍历的最佳结果for(int j=0; j<ANT_NUM; j++){if(ant_best.length>ants[j].length){ant_best=ants[j];}}UpdateInfo();printf("第%d次迭代最优路径长度是%lf\n", i,ant_best.length);printf("\n");}}
};
int main()
{srand(seed);TSP tsp;tsp.Init();tsp.Search();printf("最短路径如下\n");for(int i=0;i<CITY_NUM;i++){printf("%d",tsp.ant_best.path[i]);if(i<CITY_NUM-1)printf("->");elseprintf("\n");}return 0;
}
ACO算法在迭代构造解的过程之中应用到的信息包括以下两个方面:1) 算例的启发式信息(如路径问题中的距离);2) 反应蚂蚁路径搜索轨迹的信息素。
ACO中蚂蚁的行为细节
给定一个图网络 G=(C,L),其中 C表示图的组成成分(节点),L表示图的边。在执行ACO算法构造解的过程中,可以使用**“hard way”来构造的解,所有的解均不可以违反约束,也可以使用“soft way”**来构造解,某些解可以违反某些约束,但是这种解需要根据违反约束的程度来添加惩罚项(penalization)。
定义信息素 τ \tau τ若信息素和网络中的节点相关联, τij若信息素和网络中的边相关联;启发式信息 ηi若和节点相关联, ηij若和边相关联)。在ACO中,系统之中的每一个蚂蚁 k具有以下特点:
1)它通过探索网络 G=(C,L)来构造费用最小的解方案;
2)每一个蚂蚁k会有一个记录自己访问过路基的记忆 Mk,这个记忆信息可以用来继续构造可行解,来评判已经得到的解的优劣和更新信息素。
3)当蚂蚁 k k k在状态 xr=<xr−1,i>将要向节点 j ∈ N i k移动时 Nik表示蚂蚁 k在节点 i时的可行邻域),产生的新的状态 <xr,j>可以可行或者不可行。
4)每一个蚂蚁通过概率选择函数来选择移动方向,其中概率选择函数中包含的信息有:信息素,启发式信息,蚂蚁当前记忆信息和问题约束信息。
5)当终止条件满足时,终止蚂蚁的解方案构建。若不允许产生不可行解方案,则当构造不可行时,停止构造。
6)“步进信息素更新”(step-by-step pheromone update),表示每一次添加新的节点到某个蚂蚁的解之中,都需要对这个蚂蚁的信息素进行更新。
7)“在线延迟信息素更新”(online delayed pheromone update),表示在一个解方案构造完毕之后,在回溯整个解方案进行信息素的更新。
ACO构造解的过程
一个蚁群之中的蚂蚁并发地向网络 G G G中的邻域状态进行拓展来分别构造各自的路径,他们移动的方向收到概率选择函数的指导,通过不断的移动,每一个蚂蚁都向着构造组合优化问题的解方向靠近。一旦某个蚂蚁构造成功一个解方案,这个蚂蚁评估构造的解方案的优劣并进行信息素的更新。更新完毕的信息素又会通过概率选择函数指导后续蚂蚁的解方案构造过程。
信息素的消失和维持
信息素的消失(evaporation) 是将之前蚂蚁更新的信息素随着迭代次数的增加逐渐减小的过程。信息素的消失可以有效避免解太快收敛到一个局部最优解,同时可以帮助探索新的求解空间。
信息素维持(daemon) 可以帮助提高算法局部寻优的效果,在实际操作中,可以通过选择当前解方案最优的解,将当前最优解的信息素的更新占比加大,来提高最优解对于后续寻优的影响,这个过程也称为“离线信息素更新机制”off-line pheromone update。
ACO算法的改进方法
4.1 精英策略-elitist strategy
精英策略的思想在于基于当前最优解额外的信息素更新权重,在每一次信息素更新时,对于当前全局最优解中包含的弧给与额外的信息素权重,通过系数e来实现。应用了精英策略的上式(3)变为如下所示的形式:

其中 Lgb表示当前最优解的路径长度(成本)。
4.2 等级蚂蚁体系-rank-based version of Ant System( ASrank)
ASrank是精英策略的一种拓展策略,在ACO的所有解构造完成之后,将所有的解按照成本大小从小到大进行排序,值选择前 w−1个解方案和当前最优解方案进行信息素的更新。第 r个蚂蚁的解方案对于信息素更新的权重取值为:max{0, w−r},当前最优解对于信息素更新的权重取值为: w。在 ASrank下的上式(2)的表示形式如下所示:
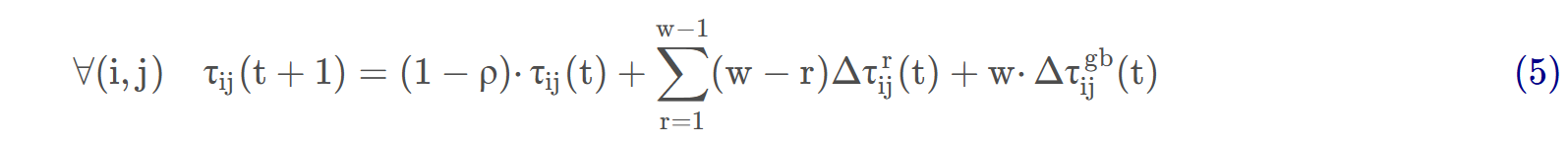
其中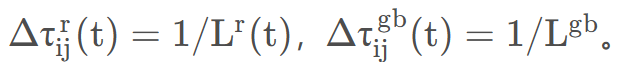
4.3 信息素重置
当连续一定迭代次数没有对当前解进行优化,或者总迭代次数达到一定的次数时,可以将信息素重置为初始化水平,从而达到改变求解空间的效果。
4.4 ACO和LS结合
在进行ACO的过程之中可以嵌入LS算法来局部优化每一个蚂蚁找到的解方案,同时优化之后的解方案被用来进行信息素的更新操作。
4.5 候选列表-candidate lists
当求解问题的邻域空间较大时,蚁群之中的蚂蚁很可能不在同一个求解空间之中,使得ACO的求解效率大大降低。为了弥补这一缺陷,可以使用候选列表的方式。对于VRPTW问题,在实际操作中,对于每一个客户点i,其候选列表包含 cl个与之距离最近的客户点,在构建解方案的过程中,首先选择候选列表中的客户点进行解方案的构建,之后再从其余客户点中选择客户点进行解方案的构建。
ACO求解VRPTW代码已上传值GitHub
https://github.com/Dragon-wang-fei-long/Huristic-code/tree/Dragon-wang-fei-long-ACO
参考文章:蚁群算法(Ant Colony Optimization,ACO)讲解+代码实现_蚁群算法的实现-CSDN博客
蚁群算法(ACO)原理梳理及应用细节 - 附求解VRPTW c++代码-阿里云开发者社区 (aliyun.com)
相关文章:
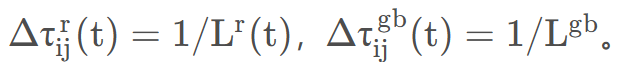
蚁群算法原理与实战(Python、MATLAB、C++)
蚁群算法 1.蚁群算法来源 蚁群算法(Ant Colony Optimization,简称ACO)是一种模拟自然界中蚂蚁寻找食物路径行为的优化算法,主要用于解决组合优化问题。它的灵感来源于意大利学者Marco Dorigo在1992年提出的蚂蚁系统模型。 蚁群算…...

HTML静态网页成品作业(HTML+CSS)——非遗阜阳剪纸介绍设计制作(1个页面)
🎉不定期分享源码,关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS,未使用Javacsript代码,共有1个页面。 二、作品演示 三、代…...
如何做萤石开放平台的物联网卡定向?
除了用萤石自带的4G卡外,我们也可以自己去电信、移动和联通办物联网卡连接萤石云平台。 1、说在前面 注意:以下流程必须全部走完,卡放在设备上才能连接到萤石云平台。 2、大致流程 登录官网→下载协议→盖章(包括骑缝章&#…...

ptrade排坑日记——定时任务执行后,文件权限会变化。
前言 今天要和大家分享的是使用ptrade的定时任务过后,执行的时候,文件权限会发生变化! 一、问题描述 定时任务执行后, /home/fly/data/fundamentals_daily/all.pickle、/home/fly/data/valuation_new/all.pickle 文件权限会从…...

TILs 评分:TCGA 肿瘤浸润淋巴细胞病理切片深度学习评分!图片下载与可视化
生信碱移 病理切片的TILs评分 TCGA 数据库是最大的肿瘤组学公开数据库之一。尽管如此,更多的研究往往仅局限于关注 TCGA 中各类肿瘤样本的上游组学信息或基本病理特征,而忽略了对样本数字化 H&E 病理染色图像的进一步应用。 ▲ TCGA中肿瘤样本的病…...

【运维】如何在浏览器中查看和管理 Cookie 信息?
如何在浏览器中查看和管理 Cookie 信息 引言 Cookie 是我们日常浏览网页时经常遇到的一个重要概念。它们用于存储用户的登录状态、偏好设置以及其他相关信息,帮助网站提供个性化的体验。然而,很多人并不清楚如何在浏览器中找到并查看这些 Cookie 信息。本文将带您了解如何在…...
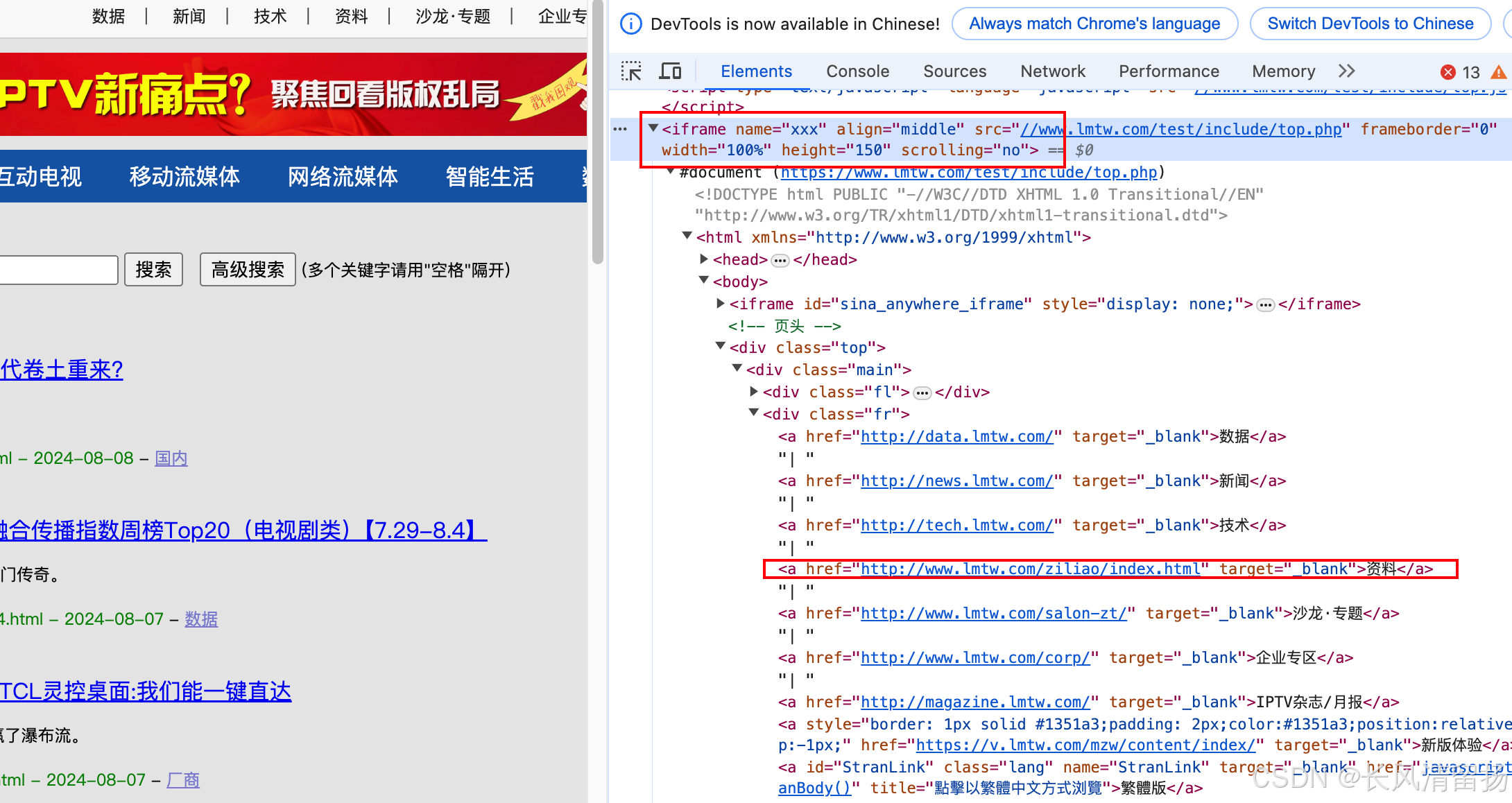
Selenium实战:深度解析Python中嵌套Frame与iFrame的定位与切换技巧,解决Selenium定位不到的问题
在Web自动化测试中,处理网页中的Frame和iFrame是常见的挑战之一。这些元素在网页中扮演着承载独立HTML文档的角色,使得直接定位或操作其中的元素变得复杂。Python的Selenium库提供了强大的工具来应对这些挑战,本文将详细介绍如何使用Selenium…...

机器学习笔记六-朴素贝叶斯
朴素贝叶斯(Naive Bayes) 是一种基于贝叶斯定理的简单而强大的分类算法,特别适用于文本分类等高维数据集。它被称为“朴素”,因为它假设特征之间是相互独立的,这在现实中可能不完全成立,但这种假设在许多实…...
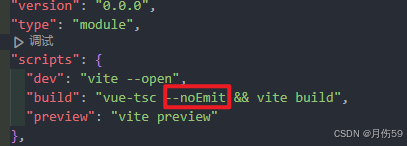
解决Vue3+Ts打包项目时会生成很多的map文件
正常打包会生成.js和.map文件 怎么去解决它呢? 正常来说我们会在vite.config.ts配置我们的项目打包方式,如下:(我这里的target:es2022是为了支持模块中顶层await的使用) // Vite 配置文件 export default…...

MeterSphere接口测试脚本断言
MeterSphere接口测试脚本断言 我们在接口自动化测试过程中,经常遇到无论我们传入什么数据信息,只要响应体报文中某个字段为不固定的特定信息(如:或1或2或3),就符合预期,流程就可以继续…...

探索顶级PDF水印API:PDFBlocks(2024年更新)
引言 在一个敏感信息常常面临风险的时代,能够轻松高效地保护文档的能力至关重要。PDF水印已成为企业和个人寻求保护其知识产权、确保文件保密性的基本工具。 PDFBlocks 文字水印 API是什么? PDFBlocks API 提供了一个强大的解决方案,用于在…...

c语言开源库之uthash用法
目录 (1)uthash介绍和下载地址 (2)uthash基本用法 1.定义自己要使用的哈希表结构体 2.初始化哈希表的头指针 3.插入数据(不同key类型对应不同函数) 4.查找数据(不同key类型对应不同函数&a…...

OurTV v3.1.1 — 完全免费,播放流畅的电视直播软件
OurTV是一款专业的魔改大屏版开源电视直播软件,与“我的电视”类似,内含丰富的电视频道,完全免费且无广告,画质清晰,播放流畅,提供良好的观影体验。此外,该软件还提供手机版。 链接:…...

精武杯的部分复现
标红的为答案 计算机手机部分 1、请综合分析计算机和⼿机检材,计算机最近⼀次登录的账户名是?admin 2.请综合分析计算机和⼿机检材,计算机最近⼀次插⼊的USB存储设备串号是?S3JKNX0JA05097Y 3.请综合分析计算机和⼿机检材,谢弘…...

verdaccio搭建npm私服
安装verdaccio npm i verdaccio -g执行命令verdaccio启动私服 verdaccio nrm启动的私 nrm use https://privateservernpm.xxx.com/添加用户 npm adduser --registry https://privateservernpm.xxx.com/发布包到私服 npm publish删除包 npm unpublish <package-nameve…...

oracle的dataguard physical standby转 snapshot standby操作文档
oracle的dataguard physical standby转 snapshot standby操作文档 一 physical standby 转 snapshot 1.1 查看 fast recovery area 是否配置 show parameter db_recovery_file_dest如果未设置或者设置太小,则需要调整 alter system set db_recovery_file_destDAT…...
:网络编程——深入详解 HTTP、HTTPS 及基于 Windows 系统的 C++ 实现)
学懂C++(四十):网络编程——深入详解 HTTP、HTTPS 及基于 Windows 系统的 C++ 实现
目录 一、引言 二、HTTP 协议 1. HTTP 概述 2. HTTP 工作原理 3. HTTP 请求和响应格式 HTTP 请求格式 4. HTTP 状态码 三、HTTPS 协议 1. HTTPS 概述 2. HTTPS 工作原理 四、基于 Windows 系统的 C 实现 1. 准备工作 2. HTTP 客户端实现 示例代码 3. HTTPS 客户…...

Element-06.案例
一.目标 实现下面这个页面,表格中的数据使用axois异步加载数据 二.实现步骤 首先在vue项目的views文件夹中新建一个tlias文件夹,用来存储该案例的相关组件。员工页面组件(EmpView.vue)和部门页面组件(DeptView.vue&…...

Axure高端交互元件库:助力产品与设计
用户体验(UX)和用户界面(UI)设计对于任何产品的成功都至关重要。为了在这个竞争激烈的市场中脱颖而出,设计师和产品开发团队需要依赖强大的工具来创造引人注目且功能丰富的交互界面。下面介绍一款Axure精心制作的"…...
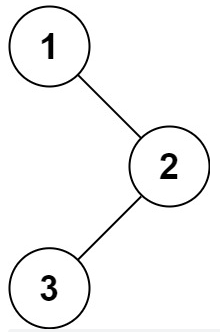
后端开发刷题 | 二叉树的前序遍历
描述 给你二叉树的根节点 root ,返回它节点值的 前序 遍历。 数据范围:二叉树的节点数量满足 1≤n≤100 ,二叉树节点的值满足 1≤val≤100,树的各节点的值各不相同 示例 1: 示例1 输入: {1,#,2,3} 返…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...
