机器学习笔记六-朴素贝叶斯
朴素贝叶斯(Naive Bayes) 是一种基于贝叶斯定理的简单而强大的分类算法,特别适用于文本分类等高维数据集。它被称为“朴素”,因为它假设特征之间是相互独立的,这在现实中可能不完全成立,但这种假设在许多实际应用中表现出令人惊讶的有效性。
贝叶斯定理
贝叶斯定理描述了在给定条件下事件发生的概率,公式如下:
P ( C ∣ X ) = P ( X ∣ C ) ⋅ P ( C ) P ( X ) P(C|X) = \frac{P(X|C) \cdot P(C)}{P(X)} P(C∣X)=P(X)P(X∣C)⋅P(C)
- (P(C|X)): 在给定特征 (X) 的情况下,类别 (C) 的后验概率。
- (P(X|C)): 在类别 (C) 给定的情况下,特征 (X) 出现的似然概率。
- (P©): 类别 © 的先验概率,即在没有给定特征时,类别的概率。
- (P(X)): 特征 (X) 的边际概率,通常可以被认为是一个常量。
朴素贝叶斯的假设
朴素贝叶斯的“朴素”假设是,特征之间是条件独立的,即:
P ( X ∣ C ) = P ( x 1 ∣ C ) ⋅ P ( x 2 ∣ C ) ⋅ … ⋅ P ( x n ∣ C ) P(X|C) = P(x_1|C) \cdot P(x_2|C) \cdot \ldots \cdot P(x_n|C) P(X∣C)=P(x1∣C)⋅P(x2∣C)⋅…⋅P(xn∣C)
其中, X = ( x 1 , x 2 , … , x n ) X = (x_1, x_2, \ldots, x_n) X=(x1,x2,…,xn) 表示特征向量的每一个特征。
朴素贝叶斯的分类过程
-
计算先验概率 (P©):
- 通过训练数据中各类别的比例来估计先验概率。
-
计算条件概率 (P(X|C)):
- 在假设特征条件独立的情况下,计算各特征在类别 (C) 下的条件概率。
-
计算后验概率 (P(C|X)):
- 使用贝叶斯定理结合先验概率和条件概率,计算出给定特征向量 (X) 时,类别 (C) 的后验概率。
-
分类决策:
- 选择后验概率最大的类别作为预测类别,即 C ^ = arg max C P ( C ∣ X ) \hat{C} = \arg\max_{C} P(C|X) C^=argmaxCP(C∣X)。
朴素贝叶斯的类型
-
高斯朴素贝叶斯(Gaussian Naive Bayes):
- 假设特征服从高斯分布,通常用于连续数据。
-
多项式朴素贝叶斯(Multinomial Naive Bayes):
- 假设特征是离散的,常用于文本分类和离散特征的数据。
-
伯努利朴素贝叶斯(Bernoulli Naive Bayes):
- 假设特征是二元变量,常用于二分类问题或文本分类中的词袋模型。
优缺点
优点:
- 速度快、效率高: 由于朴素贝叶斯算法的计算复杂度低,因此它在处理大型数据集时非常高效。
- 对高维数据表现良好: 特别适用于文本分类等高维特征数据。
- 简单易实现: 朴素贝叶斯算法非常简单且易于实现,并且在许多实际场景中表现良好。
- 适用于增量学习: 朴素贝叶斯可以方便地更新模型,适合在线学习。
缺点:
- 独立性假设不成立: 朴素贝叶斯的独立性假设在实际中往往不成立,这可能会影响模型的性能。
- 概率估计不准确: 朴素贝叶斯输出的概率并不一定可靠,尤其是在类别不平衡的情况下。
- 对数据敏感: 当某个特征在某类中未出现时,该特征的概率可能为零,影响结果(可通过拉普拉斯平滑解决)。
示例代码(使用 sklearn):
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import accuracy_score, classification_report# 示例数据:假设这是文本分类任务的词频矩阵
data = {'word1': [1, 2, 0, 1, 0],'word2': [0, 1, 0, 1, 2],'word3': [0, 0, 1, 2, 1],'word4': [1, 0, 2, 1, 1],'class': [0, 1, 0, 1, 0]
}
df = pd.DataFrame(data)# 特征和标签
X = df.drop(columns='class')
y = df['class']# 分割数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 初始化并训练朴素贝叶斯模型
model = MultinomialNB()
model.fit(X_train, y_train)# 预测和评估
y_pred = model.predict(X_test)
print(f"Accuracy: {accuracy_score(y_test, y_pred):.2f}")
print(classification_report(y_test, y_pred))
示例代码解析:
- 数据集:代码使用了一个简单的词频矩阵作为示例数据,模拟文本分类任务。
- 模型训练:使用
MultinomialNB类初始化并训练一个多项式朴素贝叶斯模型。 - 评估:通过准确率和分类报告评估模型性能。
总结
朴素贝叶斯是一种简单而高效的分类算法,特别适用于文本分类和高维数据。尽管它的独立性假设可能在现实中不成立,但在许多实际应用中,朴素贝叶斯仍能表现出色。它的实现简单,计算复杂度低,适合处理大规模数据集,是许多应用中的首选模型之一。
相关文章:

机器学习笔记六-朴素贝叶斯
朴素贝叶斯(Naive Bayes) 是一种基于贝叶斯定理的简单而强大的分类算法,特别适用于文本分类等高维数据集。它被称为“朴素”,因为它假设特征之间是相互独立的,这在现实中可能不完全成立,但这种假设在许多实…...
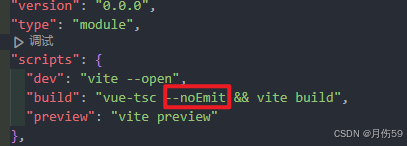
解决Vue3+Ts打包项目时会生成很多的map文件
正常打包会生成.js和.map文件 怎么去解决它呢? 正常来说我们会在vite.config.ts配置我们的项目打包方式,如下:(我这里的target:es2022是为了支持模块中顶层await的使用) // Vite 配置文件 export default…...

MeterSphere接口测试脚本断言
MeterSphere接口测试脚本断言 我们在接口自动化测试过程中,经常遇到无论我们传入什么数据信息,只要响应体报文中某个字段为不固定的特定信息(如:或1或2或3),就符合预期,流程就可以继续…...

探索顶级PDF水印API:PDFBlocks(2024年更新)
引言 在一个敏感信息常常面临风险的时代,能够轻松高效地保护文档的能力至关重要。PDF水印已成为企业和个人寻求保护其知识产权、确保文件保密性的基本工具。 PDFBlocks 文字水印 API是什么? PDFBlocks API 提供了一个强大的解决方案,用于在…...

c语言开源库之uthash用法
目录 (1)uthash介绍和下载地址 (2)uthash基本用法 1.定义自己要使用的哈希表结构体 2.初始化哈希表的头指针 3.插入数据(不同key类型对应不同函数) 4.查找数据(不同key类型对应不同函数&a…...

OurTV v3.1.1 — 完全免费,播放流畅的电视直播软件
OurTV是一款专业的魔改大屏版开源电视直播软件,与“我的电视”类似,内含丰富的电视频道,完全免费且无广告,画质清晰,播放流畅,提供良好的观影体验。此外,该软件还提供手机版。 链接:…...

精武杯的部分复现
标红的为答案 计算机手机部分 1、请综合分析计算机和⼿机检材,计算机最近⼀次登录的账户名是?admin 2.请综合分析计算机和⼿机检材,计算机最近⼀次插⼊的USB存储设备串号是?S3JKNX0JA05097Y 3.请综合分析计算机和⼿机检材,谢弘…...

verdaccio搭建npm私服
安装verdaccio npm i verdaccio -g执行命令verdaccio启动私服 verdaccio nrm启动的私 nrm use https://privateservernpm.xxx.com/添加用户 npm adduser --registry https://privateservernpm.xxx.com/发布包到私服 npm publish删除包 npm unpublish <package-nameve…...

oracle的dataguard physical standby转 snapshot standby操作文档
oracle的dataguard physical standby转 snapshot standby操作文档 一 physical standby 转 snapshot 1.1 查看 fast recovery area 是否配置 show parameter db_recovery_file_dest如果未设置或者设置太小,则需要调整 alter system set db_recovery_file_destDAT…...
:网络编程——深入详解 HTTP、HTTPS 及基于 Windows 系统的 C++ 实现)
学懂C++(四十):网络编程——深入详解 HTTP、HTTPS 及基于 Windows 系统的 C++ 实现
目录 一、引言 二、HTTP 协议 1. HTTP 概述 2. HTTP 工作原理 3. HTTP 请求和响应格式 HTTP 请求格式 4. HTTP 状态码 三、HTTPS 协议 1. HTTPS 概述 2. HTTPS 工作原理 四、基于 Windows 系统的 C 实现 1. 准备工作 2. HTTP 客户端实现 示例代码 3. HTTPS 客户…...

Element-06.案例
一.目标 实现下面这个页面,表格中的数据使用axois异步加载数据 二.实现步骤 首先在vue项目的views文件夹中新建一个tlias文件夹,用来存储该案例的相关组件。员工页面组件(EmpView.vue)和部门页面组件(DeptView.vue&…...

Axure高端交互元件库:助力产品与设计
用户体验(UX)和用户界面(UI)设计对于任何产品的成功都至关重要。为了在这个竞争激烈的市场中脱颖而出,设计师和产品开发团队需要依赖强大的工具来创造引人注目且功能丰富的交互界面。下面介绍一款Axure精心制作的"…...
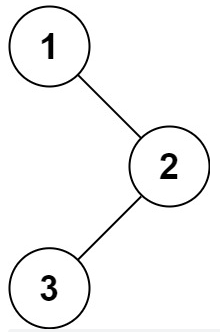
后端开发刷题 | 二叉树的前序遍历
描述 给你二叉树的根节点 root ,返回它节点值的 前序 遍历。 数据范围:二叉树的节点数量满足 1≤n≤100 ,二叉树节点的值满足 1≤val≤100,树的各节点的值各不相同 示例 1: 示例1 输入: {1,#,2,3} 返…...

自动化之响应式Web设计:纯HTML和CSS的实现技巧
大家好,我是程序员小羊! 前言 响应式Web设计是一种使Web页面在各种设备和屏幕尺寸下都能良好显示的设计方法。随着移动设备的普及,响应式设计已经成为Web开发中的标准实践。本文将探讨如何使用纯HTML和CSS实现响应式Web设计,覆…...

SolarMarker 正在使用水坑攻击与伪造的 Chrome 浏览器更新进行攻击
在过去的三个月里,eSentire 的安全研究团队发现信息窃密恶意软件 SolarMarker 都没有发动攻击,却在最近忽然重返舞台。此前,SolarMarker 的运营者使用 SEO 投毒或者垃圾邮件来引诱受害者,受害者试图下载一些文档的免费模板&#x…...

uView的u-notice-bar组件横向滚动不生效问题解决
uView的u-notice-bar组件横向滚动不生效问题解决 此问题导致我换了vant组件的 notice-bar,一度以为是该组件存在bug。uniapp中有vant组件打包小程序又是一个问题,于是乎不得不回来继续折腾uView的u-notice-bar组件,偶然发现css属性animation-…...

基于免疫算法的最优物流仓储点选址方案MATLAB仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.本算法原理 5.完整程序 1.程序功能描述 基于免疫算法的最优物流仓储点选址方案MATLAB仿真。 2.测试软件版本以及运行结果展示 MATLAB2022A版本运行 (完整程序运行后无水印) 3…...

基于Java爬取微博数据(三) 微博主页用户数据
基于Java爬取微博数据三 微博主页用户数据 数据分析爬取数据注意点 上一篇文章简单讲述了基于Java爬取微博数据(二),那么这篇将讲述如何基于 Java 爬取微博主页用户数据,下面开始具体的操作。 数据分析 在开始爬取微博主页用户数据之前,我们…...

Openstack 与 Ceph集群搭建(中): Ceph部署
文章目录 一、部署前说明1. ceph 版本选择依据2. ceph网络要求3. 硬件要求 二、部署架构三、部署过程1. 通用步骤2. 部署管理节点创建账号安装Cephadm运行bootstrap 3. 登录Ceph web4. 将其他节点加入集群同步ceph key安装ceph CLI命令行添加主机节点到集群添加OSD节点将监控节…...
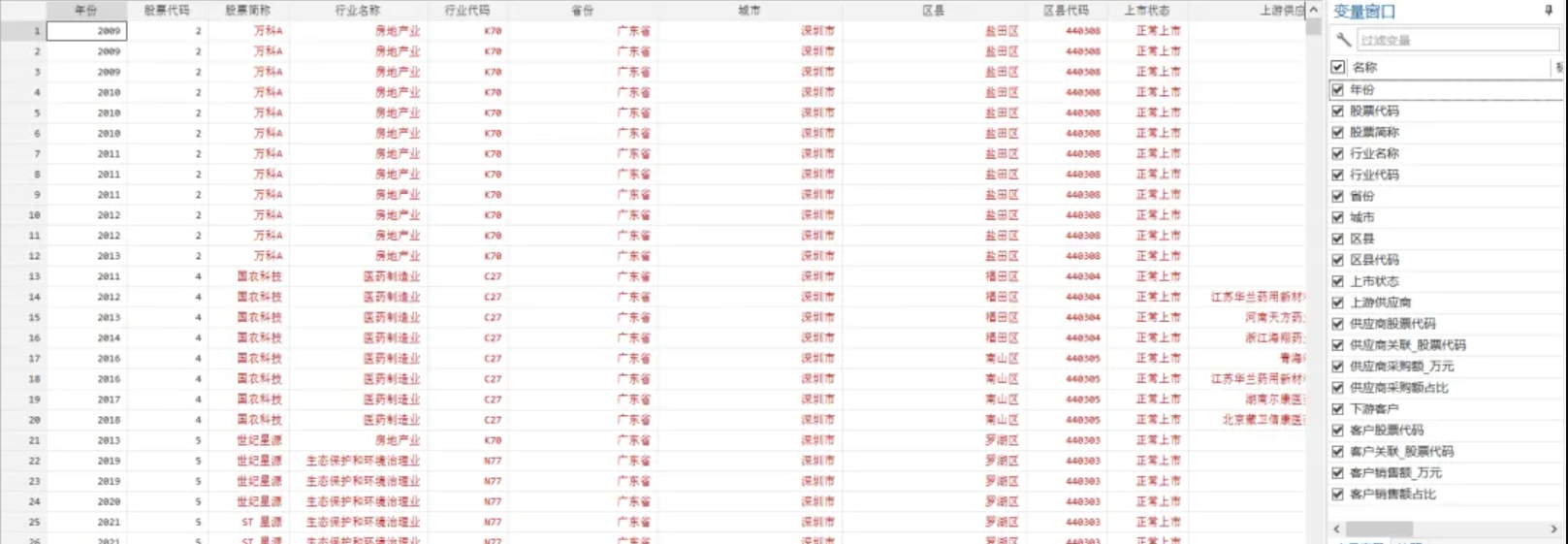
上市公司上下游、客户数据匹配数据集(2001-2023年)
参考《中国工业经济》中陶锋(2023)的做法,对上市公司的上下游供应商和客户数据进行匹配。形成“上游供应商—目标企业—下游客户一年度数据集” 一、数据介绍 数据名称:上市公司-上下游和客户数据匹配 数据范围:上市…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...
