当前位置：首页 > news >正文

机器学习第十二章-计算学习理论

news 2026/2/9 15:48:28

12.1基础知识

12.2 PAC学习

12.3有限假设空间

12.3.1可分情形

12.3.2不可分情形

12.4VC维

12.5 Rademacher复杂度

12.1基础知识

计算学习理论研究的是关于通过"计算"来进行"学习"的理论，即关于机器学习的理论基础，其目的是分析学习任务的困难本质，为学习算法提供理论保证，并根据分析结果指导算法设计。

给定样例集 = {(X1 , Y2) , (X2，Y2 )，...， (Xm , Ym)} , $x_{i}\epsilon X$ 。

令h为X到Y 的一个映射，其泛化误差为：

$E(h ; \mathcal{D})=P_{\boldsymbol{x} \sim \mathcal{D}}(h(\boldsymbol{x}) \neq y)$

h在D上的经验误差为：

$E(h ; \mathcal{D})=P_{\boldsymbol{x} \sim \mathcal{D}}(h(\boldsymbol{x}) \neq y)\widehat{E}(h ; D)=\frac{1}{m} \sum_{i=1}^{m} \mathbb{I}\left(h\left(\boldsymbol{x}_{i}\right) \neq y_{i}\right)$

后面部分将研究经验误差与泛化误差之间的逼近程度会用到几个常用不等式:

1.Jensen 不等式:对任意凸函数 f(x），有：

$f(\mathbb{E}(x)) \leqslant \mathbb{E}(f(x))$

2.HoefIding 不等式 : 若 $x_{1},x_{2}....x_{m}$ 为m个独立随机变量，且满足 $0<x_{i}<1$ ，则对任意 $\varepsilon >0$ ，有:

$\begin{array}{l} P\left(\frac{1}{m} \sum_{i=1}^{m} x_{i}-\frac{1}{m} \sum_{i=1}^{m} \mathbb{E}\left(x_{i}\right) \geqslant \epsilon\right) \leqslant \exp \left(-2 m \epsilon^{2}\right) \\ P\left(\left|\frac{1}{m} \sum_{i=1}^{m} x_{i}-\frac{1}{m} \sum_{i=1}^{m} \mathbb{E}\left(x_{i}\right)\right| \geqslant \epsilon\right) \leqslant 2 \exp \left(-2 m \epsilon^{2}\right) \end{array}$

3.McDiarmid 不等式 : 若 $x_{1},x_{2}...x_{m}$ 为m个独立随机变量，且对任意1<i<m，函数f 满足：

$\begin{array}{l} P\left(f\left(x_{1}, \ldots, x_{m}\right)-\mathbb{E}\left(f\left(x_{1}, \ldots, x_{m}\right)\right) \geqslant \epsilon\right) \leqslant \exp \left(\frac{-2 \epsilon^{2}}{\sum_{i} c_{i}^{2}}\right) \\ P\left(\left|f\left(x_{1}, \ldots, x_{m}\right)-\mathbb{E}\left(f\left(x_{1}, \ldots, x_{m}\right)\right)\right| \geqslant \epsilon\right) \leqslant 2 \exp \left(\frac{-2 \epsilon^{2}}{\sum_{i} c_{i}^{2}}\right) \end{array}$

12.2 PAC学习

计算学习理论中最基本的是概率近似正确 ( 简称 PAC) 学习理论。

PAC 辨识 :对 $0<\varepsilon ,\delta <1$ ，所有 $c\varepsilon C$ 和分布D,若存在学习算法 $\Im$ ，其输出假设 $h\epsilon \mathbb{R}$ 满足:

$P(E(h) \leqslant \epsilon) \geqslant 1-\delta$

则称学习算法 $\Im$ 能从假设空间中 PAC 辨识概念类 C.

PAC 可学习 : 令m表示从分布D中独立同分布采样得到的样例数目， $0<\varepsilon ,\delta <1$ ，对所有分布D，若存在学习算法￡和多项式函数poly,使得对任何m>poly.

PAC 学习算法: 若学习算法 $\Im$ 使概念类 C为PAC 可学习的，且 $\Im$ 的运行时间也多项式函数 poly ，则称概念类 C 是高效 PAC 可学习的，称 $\Im$ 为概念类C的 PAC 学习算法.

样本复杂度 : 满足 PAC 学习算法 $\Im$ 所需的 m> poly 中最小的m，称为学习算法 $\Im$ 的样本复杂度.

12.3有限假设空间

12.3.1可分情形

可分情形意味着目标概念c属于假设空间H，即 $c\epsilon H$ 。对 PAC 学习来说，只要训练集D 的规模能使学习算法 $\Im$ 以概率 $1-\delta$ 找到目标假设的 $\varepsilon$ 近似即可.

我们先估计泛化误差大于 $\varepsilon$ 但在训练集上仍表现完美的假设出现的概率. 假定 h的泛化误差大于 $\varepsilon$ ，对分布 D上随机来样而得的任何样例 (x y)有：

$P(E(h) \leqslant \epsilon) \geqslant 1-\delta\begin{aligned} P(h(\boldsymbol{x})=y) & =1-P(h(\boldsymbol{x}) \neq y) \\ & =1-E(h) \\ & <1-\epsilon \end{aligned}$

由于D包含 m个从 D 独立同分布采样而得的样例，因此,h与D 表现一致的概率为：

$\begin{aligned} P\left(\left(h\left(\boldsymbol{x}_{1}\right)=y_{1}\right) \wedge \ldots \wedge\left(h\left(\boldsymbol{x}_{m}\right)=y_{m}\right)\right) & =(1-P(h(\boldsymbol{x}) \neq y))^{m} \\ & <(1-\epsilon)^{m} \end{aligned}$

12.3.2不可分情形

引理：若训练集D包含m个从分布D上独立同分布采样而得的样例， $0<\varepsilon <1$ ，则对任意 $h\epsilon H$ ，有： $\begin{array}{l} P(\widehat{E}(h)-E(h) \geqslant \epsilon) \leqslant \exp \left(-2 m \epsilon^{2}\right) \\ P(E(h)-\widehat{E}(h) \geqslant \epsilon) \leqslant \exp \left(-2 m \epsilon^{2}\right) \\ P(|E(h)-\widehat{E}(h)| \geqslant \epsilon) \leqslant 2 \exp \left(-2 m \epsilon^{2}\right) \end{array}$

推论：若训练集D 包含 m个从分布 D上独立同分布来样而得的样例， $0<\varepsilon <1$ ，则对任意 $h\epsilon H$ ，以至少 $1-\delta$ 的概率成立:

$\widehat{E}(h)-\sqrt{\frac{\ln (2 / \delta)}{2 m}} \leqslant E(h) \leqslant \widehat{E}(h)+\sqrt{\frac{\ln (2 / \delta)}{2 m}}$

定理：若H为有限假设空间， $0<\varepsilon <1$ ，则对任意 $h\epsilon H$ ，有：

$P\left(|E(h)-\widehat{E}(h)| \leqslant \sqrt{\frac{\ln |\mathcal{H}|+\ln (2 / \delta)}{2 m}}\right) \geqslant 1-\delta$

12.4VC维

现实学习任务所面临的通常是无限假设空间，欲对此种情形的可学习性进行研究，需度量假设空间的复杂度.最常见的办法是考虑假设空间的 "VC维"。
1. 增长函数
增长函数，也称为VC维增长函数，描述了在给定假设空间下，能够被假设空间所“分割”或“覆盖”的训练样本的最大数量。具体来说，它衡量的是假设空间中能够对样本集进行不同标签分配的能力。增长函数的定义如下：对于一个假设空间 H )和一个样本集 S （大小为 m ），增长函数 ( $M_{H}(m)$ ) 表示假设空间 H 能够对样本集 S 进行的不同标签分配的最大数量。

2. 打分
打分是一个与增长函数紧密相关的概念。它描述了一个假设空间能否对某个样本集进行所有可能的标签分配。具体来说：一个假设空间 (H )能打分一个样本集 S （大小为 m，如果 H 中的假设可以对 S 中的每一种可能的标签分配进行匹配。

3. 打散
打散（或称为分裂）是一个与打分相关的概念，描述了假设空间能否在所有可能的标签分配下对样本集进行准确的分类。具体来说：假设空间 H 能打散一个样本集S （大小为 m ）如果H能对 S 中的每一种标签分配进行正确的分类。换句话说，如果假设空间 H 能生成所有可能的标签分配。

4. VC维
VC维是衡量一个假设空间复杂度的指标，它反映了假设空间能够打散的最大样本集的大小。具体来说：VC维是一个假设空间 H 可以打散的最大样本集的大小。即，如果假设空间 H 能打散大小为 d 的样本集，但不能打散大小为 d+1 的样本集，那么 H 的VC维就是 d。

增长函数 衡量假设空间对样本集进行的标签分配的能力。
打分描述假设空间是否能够覆盖所有可能的标签分配。
打散具体指假设空间对样本集进行所有可能标签分配的能力。
VC维 是衡量假设空间复杂度的关键指标，反映了最大打散能力。

12.5 Rademacher复杂度

Rademacher 复杂度是另一种刻画假设空间复杂度的途径，与 vc 维不同的是，它在一定程度上考虑了数据分布.

给定训练集 ={(X1 , Y2), (X2，Y2)，...， (Xm , Ym)} 假设h 的经验误差为:

$\begin{aligned} \widehat{E}(h) & =\frac{1}{m} \sum_{i=1}^{m} \mathbb{I}\left(h\left(\boldsymbol{x}_{i}\right) \neq y_{i}\right) \\ & =\frac{1}{m} \sum_{i=1}^{m} \frac{1-y_{i} h\left(\boldsymbol{x}_{i}\right)}{2} \\ & =\frac{1}{2}-\frac{1}{2 m} \sum_{i=1}^{m} y_{i} h\left(\boldsymbol{x}_{i}\right) \end{aligned}$

经验误差最小的假设是:

$\underset{h \in \mathcal{H}}{\arg \max } \frac{1}{m} \sum_{i=1}^{m} y_{i} h\left(\boldsymbol{x}_{i}\right)$

$\sigma _{i}$ 是Rademacher 随机变量.

函数空间 F 关于 Z 的经验 Rademacher 复杂度:

$\widehat{R}_{Z}(\mathcal{F})=\mathbb{E}_{\boldsymbol{\sigma}}\left[\sup _{f \in \mathcal{F}} \frac{1}{m} \sum_{i=1}^{m} \sigma_{i} f\left(\boldsymbol{z}_{i}\right)\right]$

函数空间 F 关于Z 上分布D的 Rademacher 复杂度：

$R_{m}(\mathcal{F})=\mathbb{E}_{Z \subseteq \mathcal{Z}:|Z|=m}\left[\widehat{R}_{Z}(\mathcal{F})\right]$

机器学习第十二章-计算学习理论

12.1基础知识

12.2 PAC学习

12.3有限假设空间

12.3.1可分情形

12.3.2不可分情形

12.4VC维

12.5 Rademacher复杂度

相关文章：

机器学习第十二章-计算学习理论

Java-自定义注解操作日志记录处理（@Pointcut注解不是必须的）

【c++】深入理解别名机制--引用

简便的qemu img扩容方法

EPERM: operation not permitted,

将Centos 8 Linux内核版本升级或降级到指定版本

小程序商城被盗刷，使用SCDN安全加速有用吗？

nginx的基本使用与其日志

linux | 苹果OpenCL(提高应用软件如游戏、娱乐以及科研和医疗软件的运行速度和响应)

算法-UKF中Sigma点生成

精选五款热门骨传导耳机分享，让你避免踩坑的陷阱

「字符串」前缀函数|KMP匹配：规范化next数组 / LeetCode 28（C++）

python人工智能002：jupyter基本使用

Linux使用 firewalld管理防火墙命令

二叉树（三）

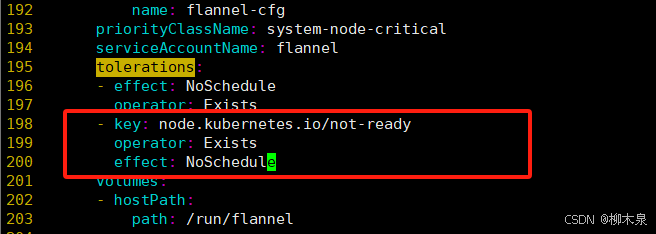
05--kubernetes组件与安装

EmguCV学习笔记 VB.Net和C# 下的OpenCv开发 C# 目录

探索TensorFlow：深度学习的未来

探索地理空间分析的新世界：Geopandas的魔力

如何为网站申请免费SSL证书？

如何在看板中体现优先级变化

全球首个30米分辨率湿地数据集(2000—2022)

selenium学习实战【Python爬虫】

dify打造数据可视化图表

HDFS分布式存储 zookeeper

排序算法总结（C++）

【JVM】Java虚拟机（二）——垃圾回收

自然语言处理——文本分类

Xcode 16 集成 cocoapods 报错

aurora与pcie的数据高速传输