使用C++编写一个AVL的增删改查代码并附上代码解释
//qq460219753提供其他代码帮助
#include <iostream>
using namespace std;struct Node
{int data;Node *left;Node *right;int height;
};// 获取结点高度
int height(Node *node)
{if (node == nullptr){return 0;}return node->height;
}// 获取两个数中较大的一个
int max(int a, int b)
{return (a > b) ? a : b;
}// 创建新结点
Node *newNode(int data)
{Node *node = new Node();node->data = data;node->left = nullptr;node->right = nullptr;node->height = 1;return node;
}// 右旋操作
Node *rightRotate(Node *y)
{Node *x = y->left;Node *T2 = x->right;// 进行旋转x->right = y;y->left = T2;// 更新高度y->height = max(height(y->left), height(y->right)) + 1;x->height = max(height(x->left), height(x->right)) + 1;// 返回新的根结点return x;
}// 左旋操作
Node *leftRotate(Node *x)
{Node *y = x->right;Node *T2 = y->left;// 进行旋转y->left = x;x->right = T2;// 更新高度x->height = max(height(x->left), height(x->right)) + 1;y->height = max(height(y->left), height(y->right)) + 1;// 返回新的根结点return y;
}// 获取平衡因子
int getBalanceFactor(Node *node)
{if (node == nullptr){return 0;}return height(node->left) - height(node->right);
}// 插入结点
Node *insert(Node *node, int data)
{if (node == nullptr){return newNode(data);}if (data < node->data){node->left = insert(node->left, data);}else if (data > node->data){node->right = insert(node->right, data);}else{return node;}// 更新高度node->height = 1 + max(height(node->left), height(node->right));// 获取平衡因子int balanceFactor = getBalanceFactor(node);// 左旋操作if (balanceFactor > 1 && data < node->left->data){return rightRotate(node);}// 右旋操作if (balanceFactor < -1 && data > node->right->data){return leftRotate(node);}// 左右旋操作if (balanceFactor > 1 && data > node->left->data){node->left = leftRotate(node->left);return rightRotate(node);}// 右左旋操作if (balanceFactor < -1 && data < node->right->data){node->right = rightRotate(node->right);return leftRotate(node);}// 返回不需要平衡的结点return node;
}
// 获取最小值结点
Node *minValueNode(Node *node)
{Node *current = node;// 找到最左侧结点while (current->left != nullptr){current = current->left;}return current;
}
// 删除结点
Node *deleteNode(Node *root, int data)
{if (root == nullptr){return root;}// 寻找要删除的结点if (data < root->data){root->left = deleteNode(root->left, data);}else if (data > root->data){root->right = deleteNode(root->right, data);}else{// 结点只有一个孩子结点或没有孩子结点if ((root->left == nullptr) || (root->right == nullptr)){Node *temp = root->left ? root->left : root->right;// 没有孩子结点的情况if (temp == nullptr){temp = root;root = nullptr;}else{*root = *temp;}delete temp;}else{// 结点有两个孩子结点Node *temp = minValueNode(root->right);root->data = temp->data;root->right = deleteNode(root->right, temp->data);}}// 如果树中只有一个结点,则返回if (root == nullptr){return root;}// 更新高度root->height = 1 + max(height(root->left), height(root->right));// 获取平衡因子int balanceFactor = getBalanceFactor(root);// 左旋操作if (balanceFactor > 1 && getBalanceFactor(root->left) >= 0){return rightRotate(root);}// 右旋操作if (balanceFactor < -1 && getBalanceFactor(root->right) <= 0){return leftRotate(root);}// 左右旋操作if (balanceFactor > 1 && getBalanceFactor(root->left) < 0){root->left = leftRotate(root->left);return rightRotate(root);}// 右左旋操作if (balanceFactor < -1 && getBalanceFactor(root->right) > 0){root->right = rightRotate(root->right);return leftRotate(root);}// 返回不需要平衡的结点return root;
}// 查找结点
Node *search(Node *node, int data)
{if (node == nullptr || node->data == data){return node;}if (node->data < data){return search(node->right, data);}return search(node->left, data);
}// 中序遍历
void inorder(Node *root)
{if (root != nullptr){inorder(root->left);cout << root->data << " ";inorder(root->right);}
}int main()
{Node *root = nullptr;// 插入结点root = insert(root, 10);root = insert(root, 20);root = insert(root, 30);root = insert(root, 40);root = insert(root, 50);root = insert(root, 25);// 中序遍历树cout << "Inorder traversal of the AVL tree is: " << endl;inorder(root);cout << endl;// 删除结点root = deleteNode(root, 25);// 中序遍历树cout << "Inorder traversal of the AVL tree after deleting 25 is: " << endl;inorder(root);cout << endl;return 0;
}运行结果如下
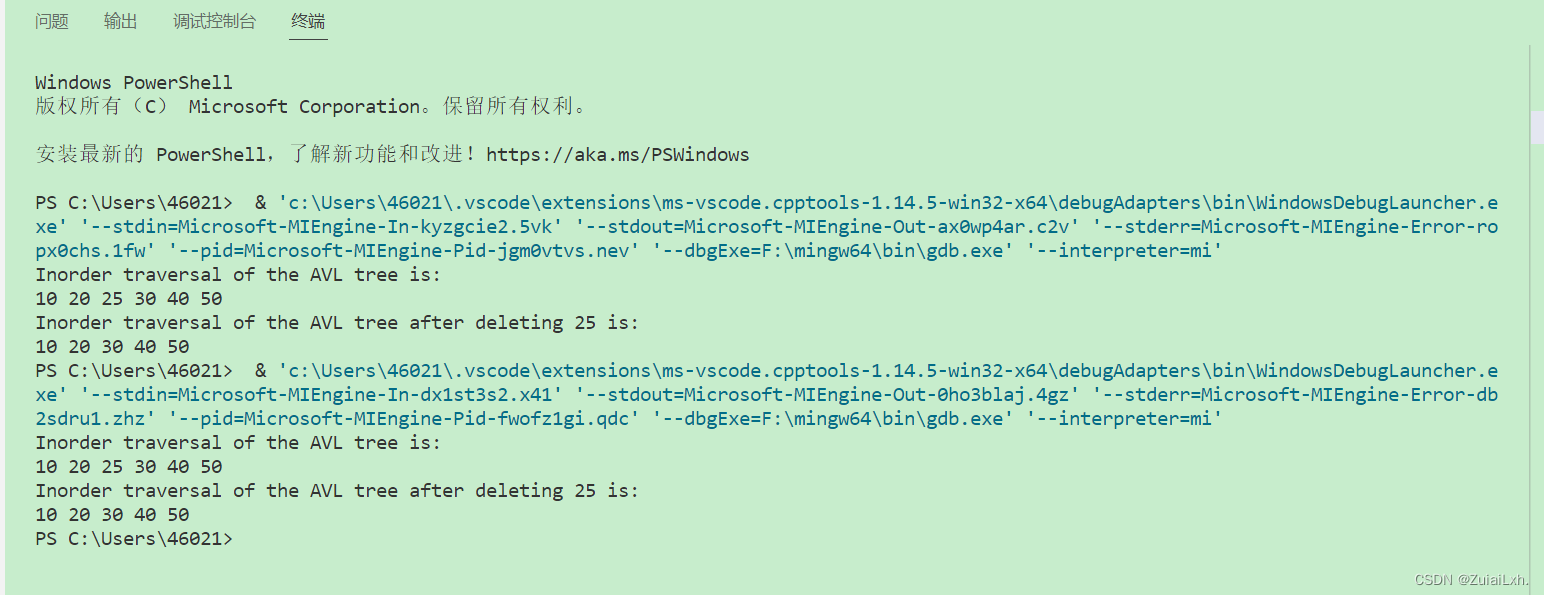
代码解释:
Node 结构体定义:定义了 AVL 树结点的数据结构。
height 函数:用于获取结点的高度,如果结点为空则返回 -1。
getBalanceFactor 函数:用于获取结点的平衡因子,平衡因子为左子树的高度减去右子树的高度。
leftRotate 函数:用于左旋操作。
rightRotate 函数:用于右旋操作。
insert 函数:用于插入结点。首先进行普通的二叉搜索树插入操作,然后对树进行平衡操作。
minValueNode 函数:用于获取 AVL 树中最小的结点。
deleteNode 函数:用于删除结点。首先进行普通的二叉搜索树删除操作,然后对树进行平衡操作。
search 函数:用于查找结点。
inorder 函数:用于中序遍历 AVL 树。
main 函数:创建 AVL 树,插入结点,进行中序遍历,删除结点,再次进行中序遍历。
相关文章:

使用C++编写一个AVL的增删改查代码并附上代码解释
//qq460219753提供其他代码帮助 #include <iostream> using namespace std;struct Node {int data;Node *left;Node *right;int height; };// 获取结点高度 int height(Node *node) {if (node nullptr){return 0;}return node->height; }// 获取两个数中较大的一个 i…...

React/ReactNative 状态管理: redux-toolkit 如何使用
有同学反馈开发 ReactNative 应用时状态管理不是很明白,接下来几篇文章我们来对比下 React 及 ReactNative 状态管理常用的几种框架的使用和优缺点。 上一篇文章介绍了 redux 的使用,这篇文章我们来看下 redux 的升级版:redux-toolkit。 下…...

14基于双层优化的电动汽车优化调度研究
说明书 MATLAB代码:基于双层优化的电动汽车优化调度研究 关键词:双层优化 选址定容 输配协同 时空优化 参考文档:《考虑大规模电动汽车接入电网的双层优化调度策略_胡文平》中文版 《A bi-layer optimization based temporal and sp…...

古茗科技面试:为什么 ElasticSearch 更适合复杂条件搜索?
文章目录 ElasticSearch 简介倒排索引联合索引查询跳表合并策略Bitset 合并策略MySQL 最多使用一个条件涉及的索引来过滤,然后剩余的条件只能在遍历行过程中进行内存过滤。 上述这种处理复杂条件查询的方式因为只能通过一个索引进行过滤,所以需要进行大量的 I/O 操作来读取行…...
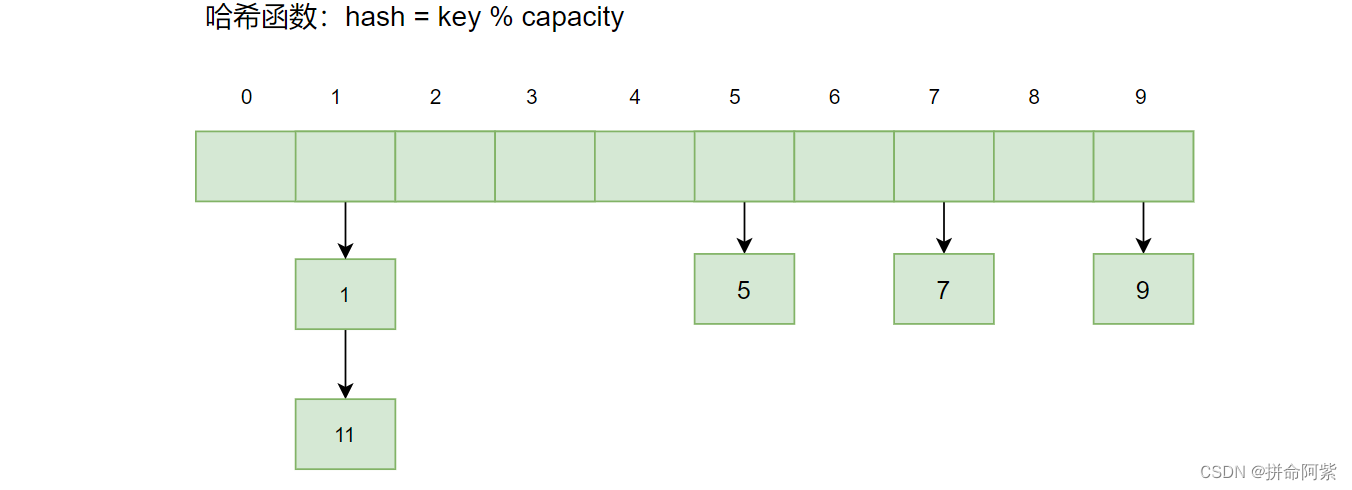
【数据结构】哈希表
目录 1、哈希表 1.1 哈希表的简介 1.2 降低哈希冲突率 1.3 解决哈希冲突 1.3.1 闭散列 1.3.2 开散列(哈希桶) 1、哈希表 1.1 哈希表的简介 假设我们目前有一组数据,我们要从这组数据中找到指定的 key 值,那么咱们目…...

物联网常用协议MQTT协议相关介绍
概述 MQTT(Message Queuing Telemetry Transport)是一种轻量级的消息传输协议,旨在在网络带宽有限的情况下,为物联网设备之间的通信提供可靠的、低延迟的消息传递服务。MQTT协议具有订阅/发布模式,支持多种传输协议&a…...

【C语言进阶】13. 假期测评②
day10 1. int类型字节数 求函数返回值,传入 -1 ,则在64位机器上函数返回( ) int count 0; int x -1; while (x) {count;x x >> 1; } printf("%d", count);A: 1 B: 2 C: 32 D: 死循环,没结果 【答案解析】C xx&(x-1)这…...

【国产FPGA】国产FPGA搭建图像处理平台
最近收到了高云寄过来的FPGA板卡,下图:来源:https://wiki.sipeed.com/hardware/zh/tang/tang-primer-20k/primer-20k.htmlFPGA主要参数:FPGA型号参数GW2A-LV18PG256C8/I7逻辑单元(LUT4) 20736寄存器(FF) 15552分布式静态随机存储器S-SRAM(bit…...
你的应用太慢了,给我司带来了巨额损失,该怎么办
记得很久之前看过谷歌官方有这么样的声明:如果一个页面的加载时间从 1 秒增加到3 秒,那么用户跳出的概率将增加 32%。 但是早在 2012 年,亚马逊就计算出了,页面加载速度一旦下降一秒钟,每年就会损失 16 亿美元的销售额…...

第十四届蓝桥杯三月真题刷题训练——第 22 天
目录 第 1 题:受伤的皇后_dfs 题目描述 输入描述 输出描述 输入输出样例 运行限制 代码: 思路: 第 2 题:完全平方数 问题描述 输入格式 输出格式 样例输入 1 样例输出 1 样例输入 2 样例输出 2 评测用例规模与约…...
机器学习:朴素贝叶斯模型算法原理(含实战案例)
机器学习:朴素贝叶斯模型算法原理 作者:i阿极 作者简介:Python领域新星作者、多项比赛获奖者:博主个人首页 😊😊😊如果觉得文章不错或能帮助到你学习,可以点赞👍收藏&…...

Linux 多线程:理解线程
目录一、理解线程的思想二、Linux中的线程与进程1.Linux中的进程2.Linux中的线程三、线程的工作方式四、线程的独有数据与共享数据1.独有数据2.共享数据一、理解线程的思想 线程就是把一个进程分成多个执行部分,一个部分就是一个线程,比如可以让一个线程…...
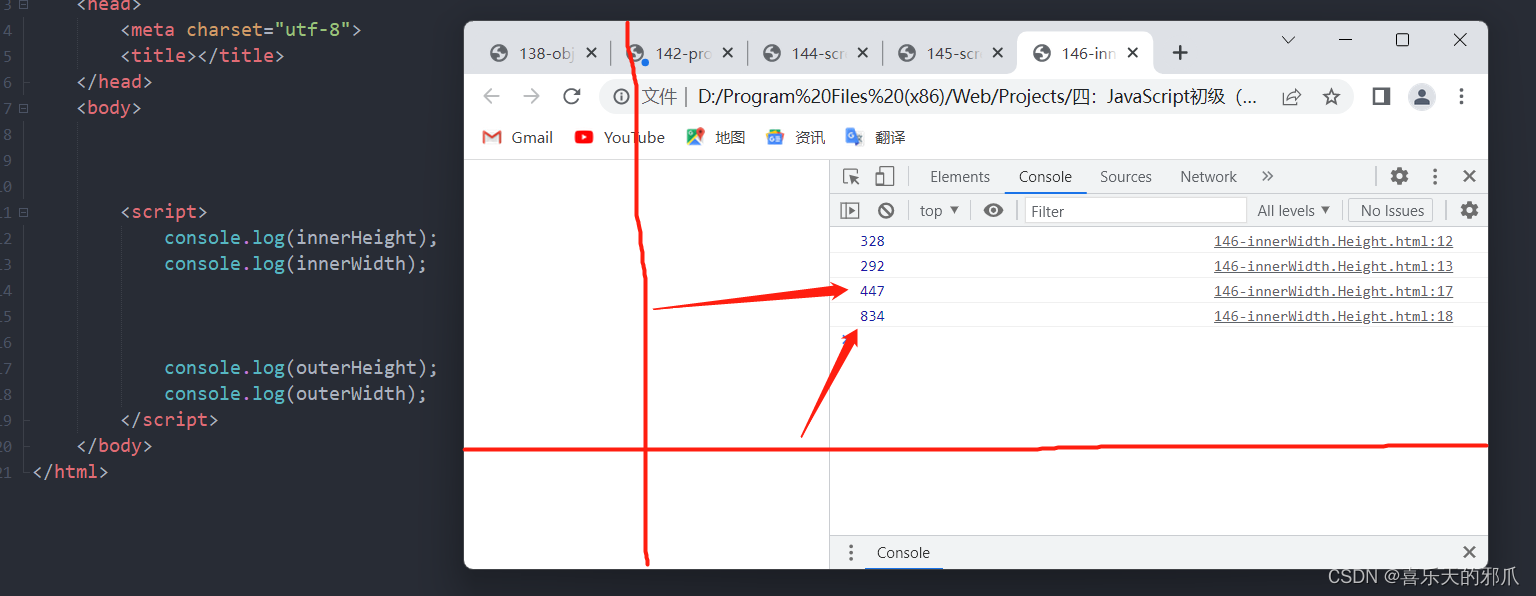
Web前端学习:章四 -- JavaScript初级(四)-- BOM
138:Object数据格式简介 1、object对象 JS中独有 的一种数据格式 名字可以随便取,值一般就那几种数据格式 139:BOM - JS跳转页面 BOM Browser Object Model:浏览器对象模型 使用JavaScript控制浏览器交互 控制浏览器里面的内…...

Lesson9.网络基础1
网络协议初识 所谓的协议就是人们为了通信的一种约定 操作系统要进行协议管理,必然会先描述,再组织协议本质就是软件,软件是可以"分层"协议在设计的时候,就是被层状的划分的, 为什么要划分成为层状结构 场景复杂功能解耦(便于人们进行各种维护)OSI七层模型 局域网中…...
这几个SQL语法的坑,你踩过吗
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址:https://github.com/…...

算法基础——复杂度
前言 算法是解决问题的一系列操作的集合。著名的计算机科学家Niklaus Wirth曾提出:算法数据结构程序,由此可见算法在编程中的重要地位。本篇主要讨论算法性能好坏的标准之一——复杂度。 1 复杂度概述 1.1 什么是复杂度 本文所讨论的复杂度是指通过事先…...

基类与派生类对象的关系 派生类的构造函数
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章,「初学」C 🔥座右铭:“不要等到什么都没有了,才下…...
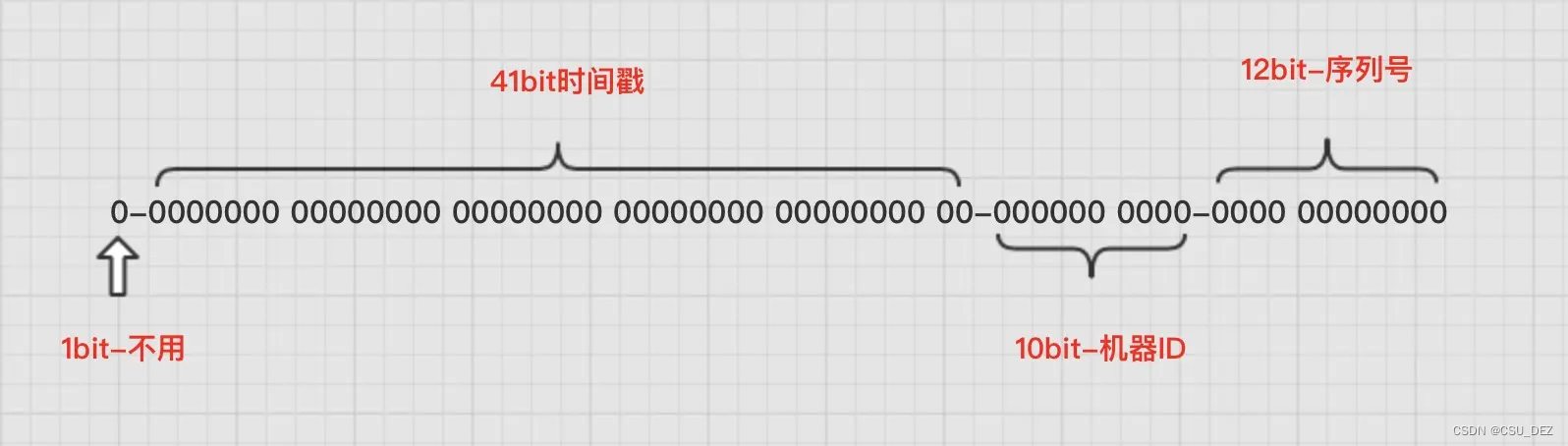
【算法】生成分布式 ID 的雪花算法
ID 是数据的唯一、不变且不重复的标识,在查询数据库的数据时必须通过 ID 查询,在分布式环境下生成全局唯一的 ID 是一个重要问题。 雪花算法(snowflake)是一种生成分布式环境下全局唯一 ID 的算法,该算法由 Twitter 发…...
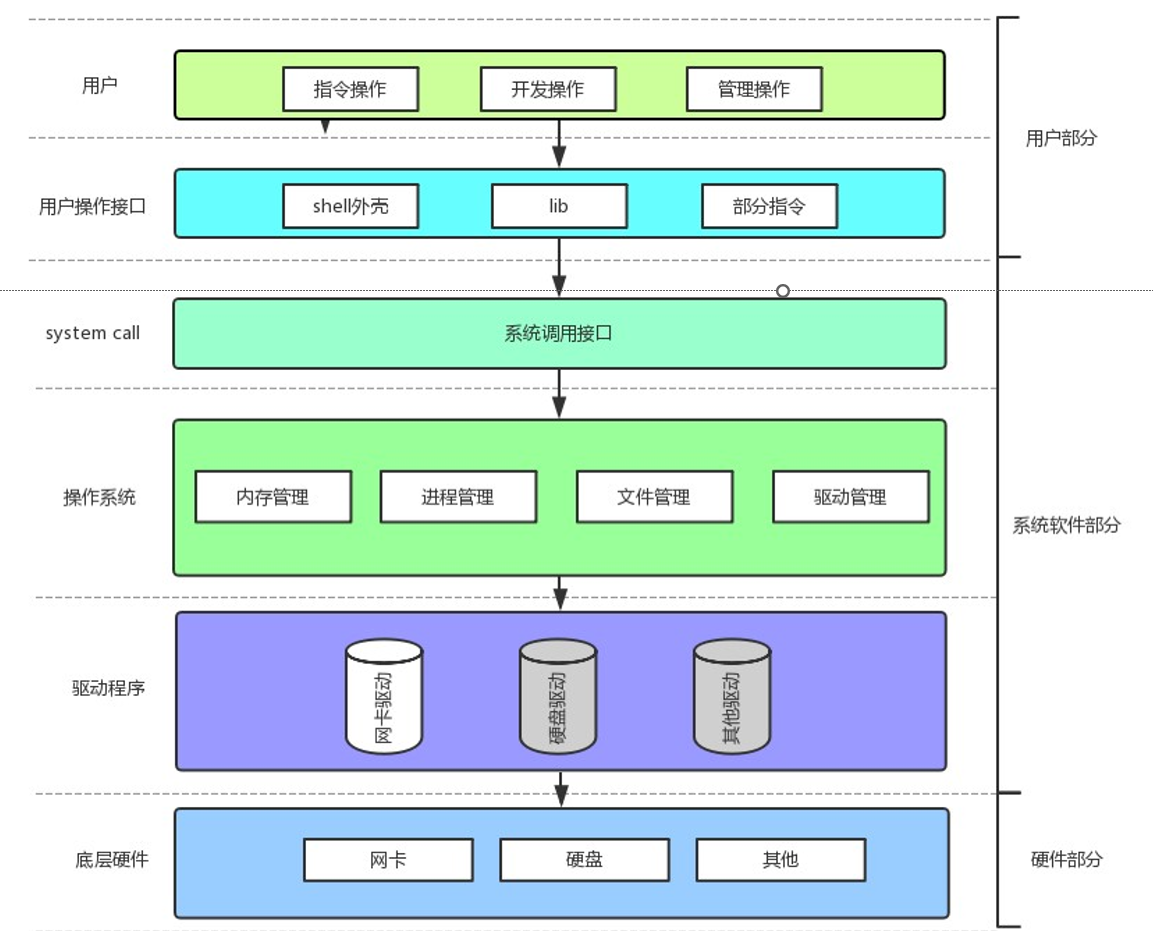
Linux系统编程 - 基础IO(IO操作)
目录 预备知识 复习C文件IO相关操作 printf相关函数 fprintf snprintf 读取文件 系统文件IO操作 open函数 umask()函数 open函数返回值 预备知识 1.你真的理解文件原理和操作了吗?不是语言问题,是系统问题2.是不是只有C/C有文件操作呢&#x…...

基于 Avue 的 CRUD 表格组件封装
在 components 文件夹中,创建一个新的 .vue 文件,例如:AvueCrudTable.vue。 透传父组件传递的属性和事件 : 1、利用v-bind=“ a t t r s " 支持所有 a v u e 的使用方法并在其基础上进行封装 2 、使用 v − o n = " attrs"支持所有 avue 的使用方法并在其基…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...
