【C++】科普:C++中的浮点数怎么在计算机中表示?
这里我们以8.25这个数为例说明计算机时如何存取float类型的数据的:
float a = 8.25;
引言
1. 所占位数
首先,明确一个概念,float类型的数据在常规计算机中通常占4个字节,也就是32位。其内存分布如图:
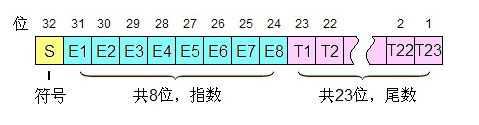
| 位字段说明 | 所占位数 | 具体含义 |
|---|---|---|
| 符号位 | 1 | 说明浮点数正负,0表示正,1表示负 |
| 指数位 | 8 | 说明浮点数的指数,也有正负,大于127为正,小于127的为负 |
| 尾数位 | 23 | 浮点数的尾数位 |
2. 科学计数法
在十进制中,我们了解科学计数法。
例如,825的科学计数法表述为:8.25*102,0.0825的科学计数法表述为:8.25*10(-2)
请注意观察这一点:整数部分的值是大于1小于10的。后面的指数部分也有正指数和负指数。
2. 计算步骤
1. 二进制表示
将8.25用二进制数表示出来:
首先:整数部分为8,二进制表示为1000;
其次,小数部分为0.25,为二进制表示计算方法和整数部分的计算方法恰恰相反,整数部分转换二进制的时候是不断除以2得到的,这里就是不断乘以2:
0.25*2 = 0.5,整数部分为0,记下:0
0.5*2 = 1.0,整数部分为1,记下:1
则0.25的二进制表示即为0.01,即1*2^(-2);
在这一阶段,我们得出结果:8.25的二进制表示为:1000.01
2. 使用科学计数法来表示
在引言里介绍了十进制的科学计数法,同理我们推理出二进制的科学计数法:
8.25的二进制表示为:1000.01;
1000.01的二进制科学计数法表示为:1.00001*2^3
请根据引言中的注意事项,可以推理出:在二进制的科学计数法中:整数部分的取值只能是1,是个固定值。
因此在表示中可以直接把这一步写死,根本不需要去表示整数部分。
3. 转化为计算机存储数据
1.00001*2^3
在引言里,我们已经知道了浮点数在计算机中的表示方法,套用这套表示方法,我们可以知道:
符号位:
8.25是一个正数,因此这位为0.
指数位:
指数位为+3,所以这里的值为127+3=130,130的二进制表示为1000 0010,因此这里为1000 0010。
尾数位:
小数位为00001,这里尾数位占用23个字节,位数不够,所以补0,因此这里为:00001后面补18个0。
4.得出结论
浮点数8.25在计算机中的二进制表示为:0 1000 0010 0000 1000 0000 0000 0000 000
相关文章:

【C++】科普:C++中的浮点数怎么在计算机中表示?
这里我们以8.25这个数为例说明计算机时如何存取float类型的数据的: float a 8.25;引言 1. 所占位数 首先,明确一个概念,float类型的数据在常规计算机中通常占4个字节,也就是32位。其内存分布如图: 位字段说明所占位…...

Linux 多线程:多线程和多进程的对比
目录一、多进程优缺点二、多线程优缺点三、使用多执行流的场景在多任务处理中,我们既可以使用多进程,也可以使用多线程。但多进程和多线程并不是随意选择的,因为它们应对的场景不同,优缺点也不同。 一、多进程优缺点 多进程就是在…...
IO流你了解多少
IO流你了解多少 🏠个人主页:shark-Gao 🧑个人简介:大家好,我是shark-Gao,一个想要与大家共同进步的男人😉😉 🎉目前状况:23届毕业生,目前在某公…...

【C++】C++ 11 新特性之auto关键字
文章目录类型别名的思考auto简介auto关键字的特性类型别名的思考 随着程序越来越复杂,程序中用到的类型也越来越复杂,经常体现在: 类型难于拼写含义不明确导致容易出错 #include <string> #include <map> int main() {std::ma…...

nodejs的后端框架egg,thinkjs,nestjs,nuxtjs,nextjs对比
1. Egg.js:优点:Egg.js是一个基于Koa的Node.js企业级应用开发框架,它提供了完整的开发规范和一套稳定性和安全性较高的架构体系,能够帮助开发者快速构建高可用、高性能的应用程序。同时,Egg.js还提供了很多自定义插件和…...

SpringBoot @SpringBootTest 无法启动服务
这几天在看Hikari、Druid连接池。按照网上代码写Junit测试类。当时代码如下: package com.ceaning.crudp.utils;import org.junit.Test; import org.springframework.beans.factory.annotation.Autowired; import org.springframework.boot.test.context.SpringBootTest; impo…...
PyTorch深度学习实战 | 神经网络的优化难题
即使我们可以利用反向传播来进行优化,但是训练过程中仍然会出现一系列的问题,比如鞍点、病态条件、梯度消失和梯度爆炸,对此我们首先提出了小批量随机梯度下降,并且基于批量随机梯度下降的不稳定的特点,继续对其做出方…...
如何缩小pdf文件的大小便于上传?在线压缩pdf工具推荐
平时在工作、学习时我们经常都需要用到pdf文件,那么当遇上需要将pdf压缩大小的时候,该使用哪种pdf压缩(https://www.yasuotu.com/pdfyasuo)方式呢?今天分享一个在线压缩pdf的方法,需要的小伙伴一起来了解…...
使用C++编写一个AVL的增删改查代码并附上代码解释
//qq460219753提供其他代码帮助 #include <iostream> using namespace std;struct Node {int data;Node *left;Node *right;int height; };// 获取结点高度 int height(Node *node) {if (node nullptr){return 0;}return node->height; }// 获取两个数中较大的一个 i…...

React/ReactNative 状态管理: redux-toolkit 如何使用
有同学反馈开发 ReactNative 应用时状态管理不是很明白,接下来几篇文章我们来对比下 React 及 ReactNative 状态管理常用的几种框架的使用和优缺点。 上一篇文章介绍了 redux 的使用,这篇文章我们来看下 redux 的升级版:redux-toolkit。 下…...

14基于双层优化的电动汽车优化调度研究
说明书 MATLAB代码:基于双层优化的电动汽车优化调度研究 关键词:双层优化 选址定容 输配协同 时空优化 参考文档:《考虑大规模电动汽车接入电网的双层优化调度策略_胡文平》中文版 《A bi-layer optimization based temporal and sp…...

古茗科技面试:为什么 ElasticSearch 更适合复杂条件搜索?
文章目录 ElasticSearch 简介倒排索引联合索引查询跳表合并策略Bitset 合并策略MySQL 最多使用一个条件涉及的索引来过滤,然后剩余的条件只能在遍历行过程中进行内存过滤。 上述这种处理复杂条件查询的方式因为只能通过一个索引进行过滤,所以需要进行大量的 I/O 操作来读取行…...
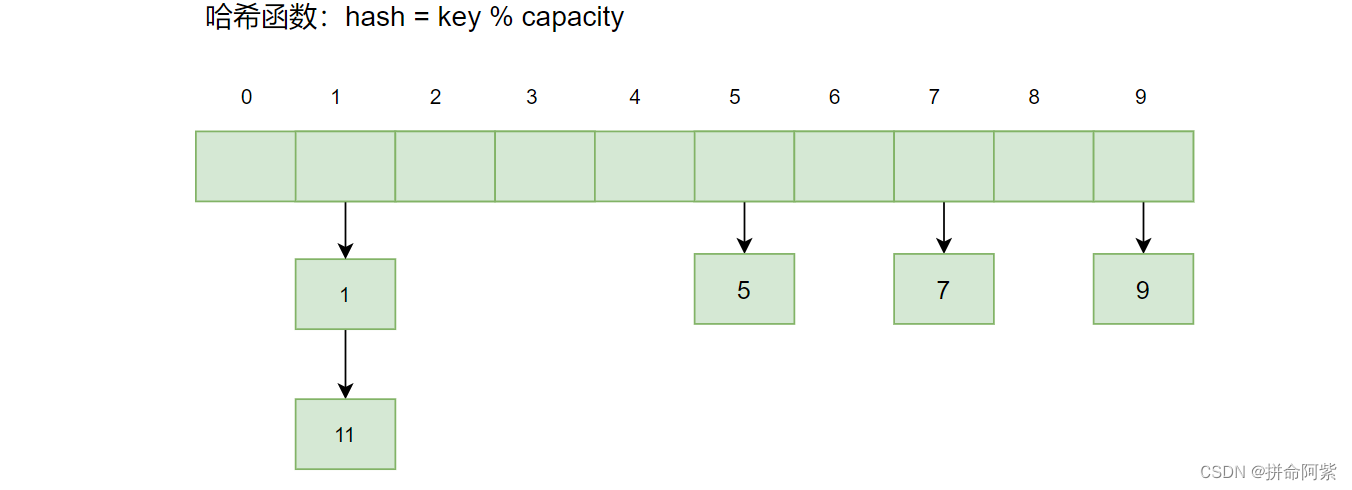
【数据结构】哈希表
目录 1、哈希表 1.1 哈希表的简介 1.2 降低哈希冲突率 1.3 解决哈希冲突 1.3.1 闭散列 1.3.2 开散列(哈希桶) 1、哈希表 1.1 哈希表的简介 假设我们目前有一组数据,我们要从这组数据中找到指定的 key 值,那么咱们目…...

物联网常用协议MQTT协议相关介绍
概述 MQTT(Message Queuing Telemetry Transport)是一种轻量级的消息传输协议,旨在在网络带宽有限的情况下,为物联网设备之间的通信提供可靠的、低延迟的消息传递服务。MQTT协议具有订阅/发布模式,支持多种传输协议&a…...

【C语言进阶】13. 假期测评②
day10 1. int类型字节数 求函数返回值,传入 -1 ,则在64位机器上函数返回( ) int count 0; int x -1; while (x) {count;x x >> 1; } printf("%d", count);A: 1 B: 2 C: 32 D: 死循环,没结果 【答案解析】C xx&(x-1)这…...

【国产FPGA】国产FPGA搭建图像处理平台
最近收到了高云寄过来的FPGA板卡,下图:来源:https://wiki.sipeed.com/hardware/zh/tang/tang-primer-20k/primer-20k.htmlFPGA主要参数:FPGA型号参数GW2A-LV18PG256C8/I7逻辑单元(LUT4) 20736寄存器(FF) 15552分布式静态随机存储器S-SRAM(bit…...
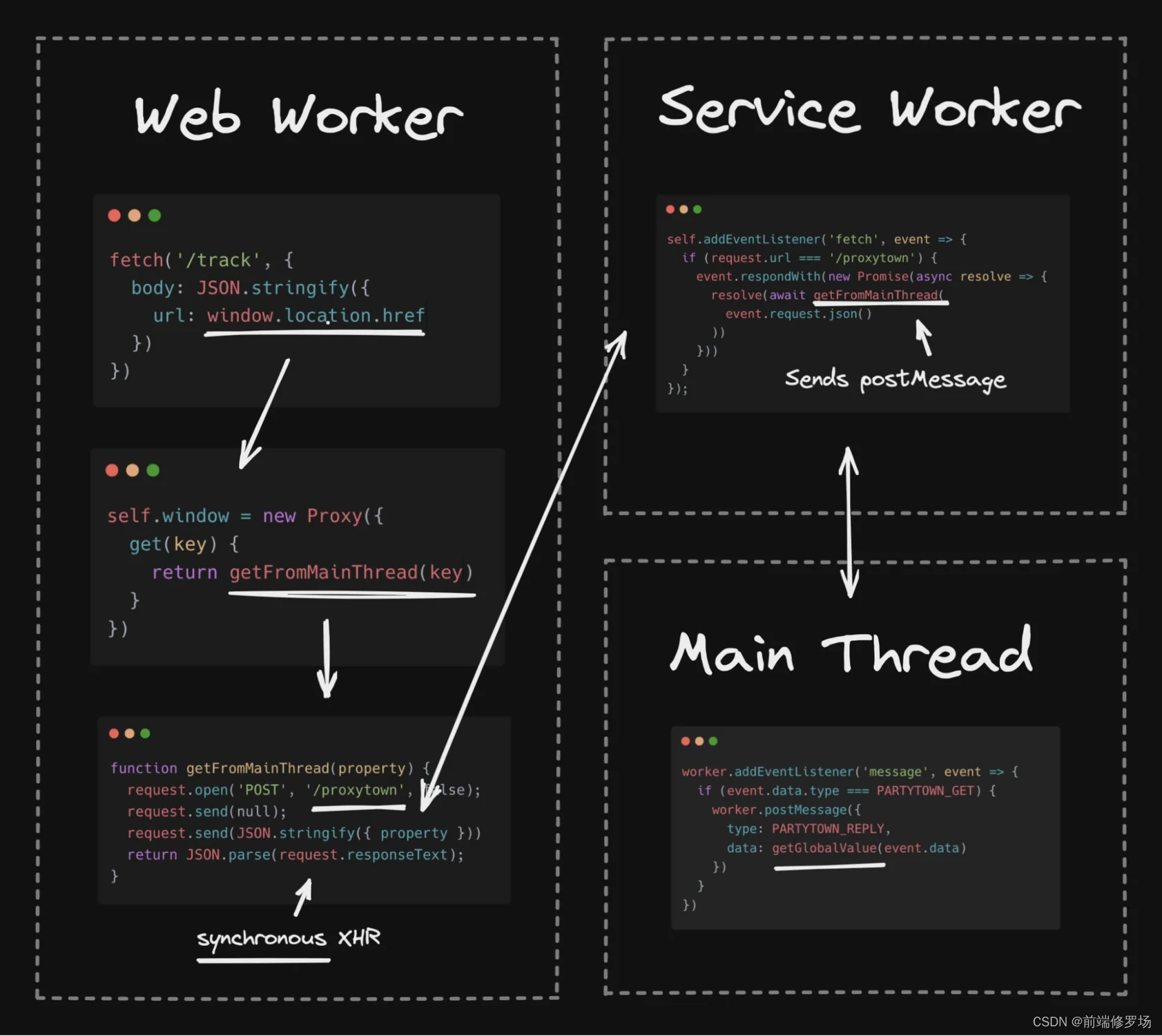
你的应用太慢了,给我司带来了巨额损失,该怎么办
记得很久之前看过谷歌官方有这么样的声明:如果一个页面的加载时间从 1 秒增加到3 秒,那么用户跳出的概率将增加 32%。 但是早在 2012 年,亚马逊就计算出了,页面加载速度一旦下降一秒钟,每年就会损失 16 亿美元的销售额…...

第十四届蓝桥杯三月真题刷题训练——第 22 天
目录 第 1 题:受伤的皇后_dfs 题目描述 输入描述 输出描述 输入输出样例 运行限制 代码: 思路: 第 2 题:完全平方数 问题描述 输入格式 输出格式 样例输入 1 样例输出 1 样例输入 2 样例输出 2 评测用例规模与约…...
机器学习:朴素贝叶斯模型算法原理(含实战案例)
机器学习:朴素贝叶斯模型算法原理 作者:i阿极 作者简介:Python领域新星作者、多项比赛获奖者:博主个人首页 😊😊😊如果觉得文章不错或能帮助到你学习,可以点赞👍收藏&…...

Linux 多线程:理解线程
目录一、理解线程的思想二、Linux中的线程与进程1.Linux中的进程2.Linux中的线程三、线程的工作方式四、线程的独有数据与共享数据1.独有数据2.共享数据一、理解线程的思想 线程就是把一个进程分成多个执行部分,一个部分就是一个线程,比如可以让一个线程…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...
