用栈实现队列(图示超详解哦)
全文目录
- 引言
- 用栈实现队列
- 题目介绍
- 思路简述
- 实现
- 栈的部分
- 队列的部分
- 创建队列
- 判断队列是否为空
- 在队列尾入
- 在队列头出
- 访问队头元素
- 释放队列
- 总结
引言
在上一篇文章中,我们了解了用两个队列实现栈。在这篇问章中将继续介绍用两个栈实现队列的OJ练习:
用栈实现队列OJ链接
在本文中可能会需要借鉴到栈与队列的实现:
戳我看栈详解哦
戳我看队列详解哦
用栈实现队列
题目介绍
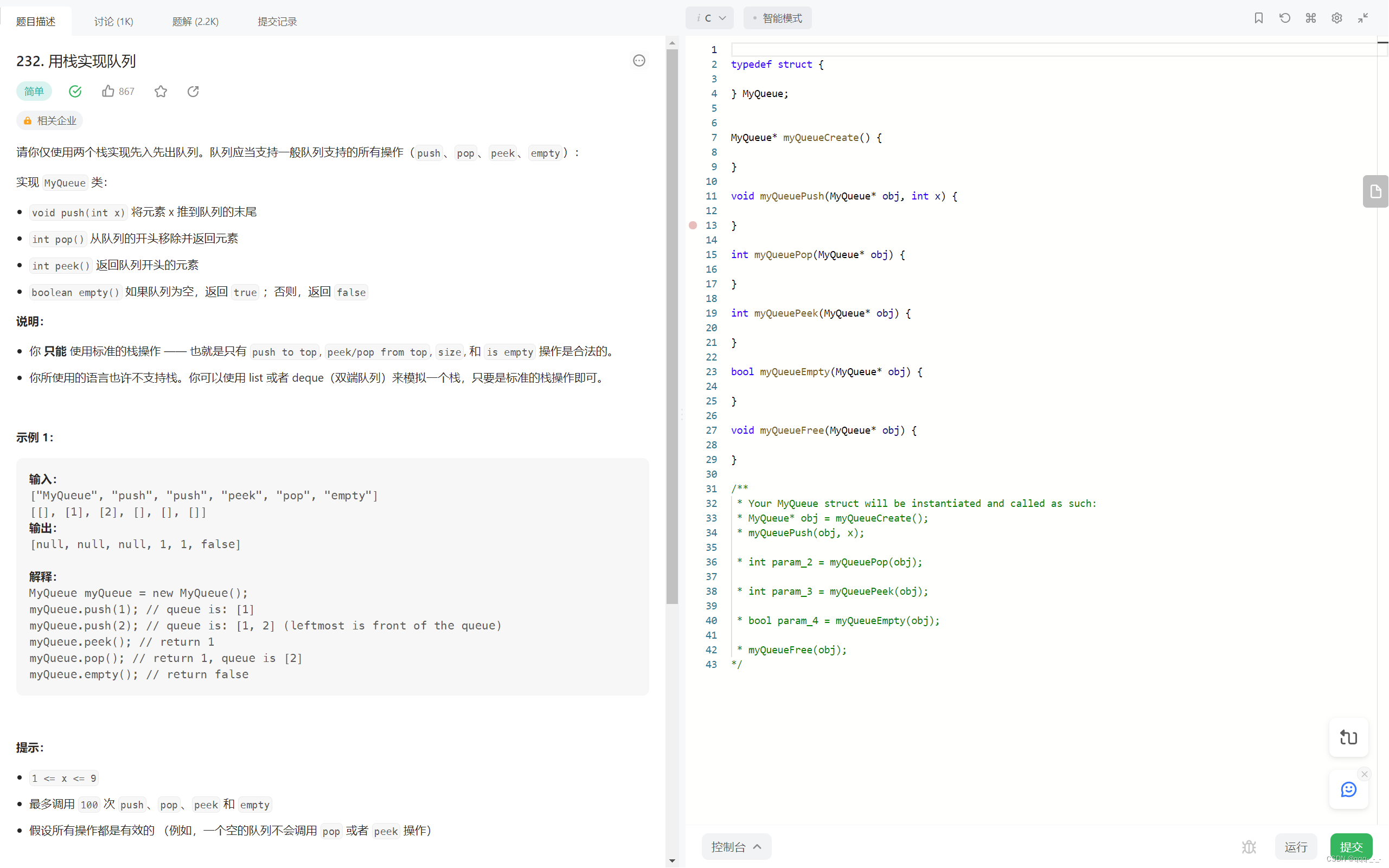
题目描述很简单:
通过两个栈实现队列存储数据的特点,即先进先出:
我们需要实现基本的队列操作:push、pop、top、empty、free:
void push(int x) 将元素 x 推到队列的末尾;
int pop() 从队列的开头移除并返回元素;
int peek() 返回队列开头的元素;
bool empty() 如果队列为空,返回 true ;否则,返回 false。
思路简述
与上一道题相同,这道题的难点同样在于结构:
如何实现pop时移除栈底的元素。由于栈是先进后出,所以栈底的元素是无法直接移除的。
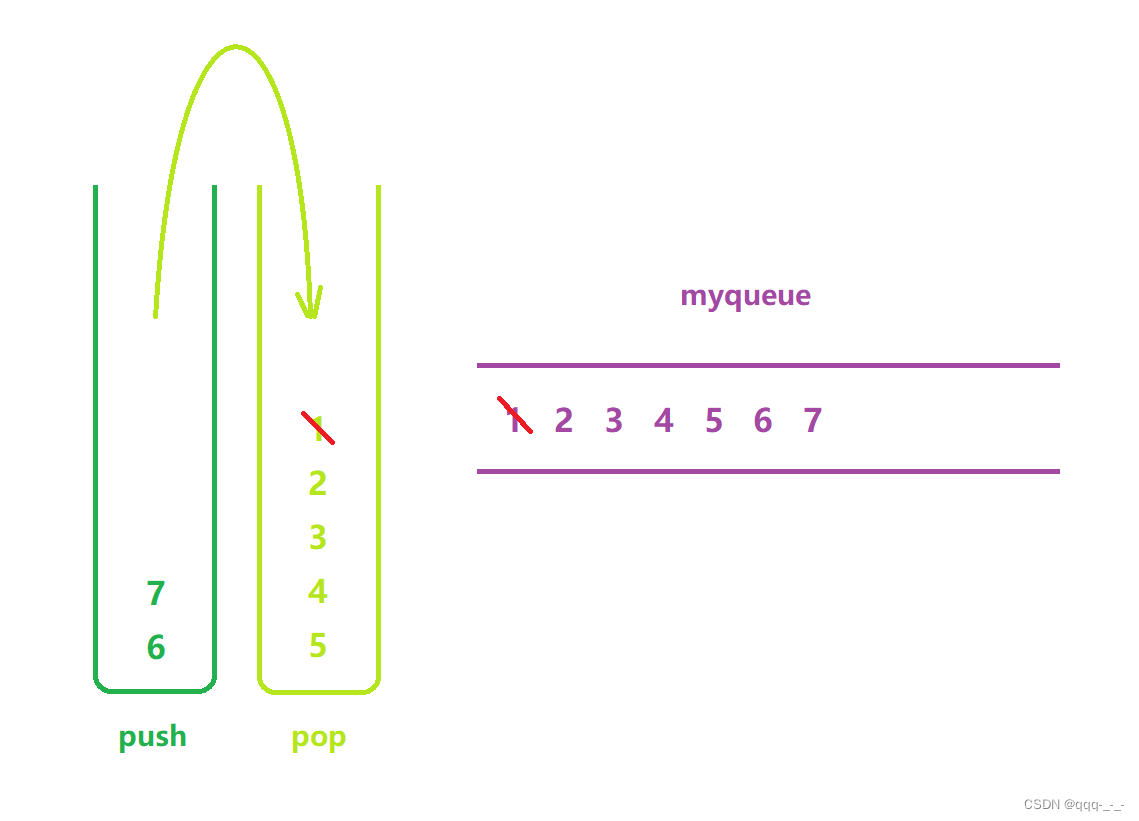
我们就可以使用第二个栈,将栈中的元素依次取出,存入第二个栈中。由于栈是先进后出,所以当将一个栈中的元素依次取出,放进另一个栈中时,数据的顺序就会颠倒,这时在栈顶的元素就是最先入栈的元素,将这个元素移除即可;
也就是说,这个栈中栈顶的元素永远是最先入栈的元素,所以在这个栈中的元素没有全部移除之前,是不能在这个栈中再插入元素了,只能在原来的那个栈中插入;
我们发现,用两个栈来实现队列时,有一个栈只用于插入元素,有一个栈只用于移除元素,所以我们可以直接将前一个栈命名为push,后一个命名为pop;
如果pop栈为空,又需要移除元素时,才需要将push栈中的元素倒到pop栈中:
实现
栈的部分
在用两个栈实现队列之前,我们首先需要实现栈的接口。在需要用到栈的操作时直接复用即可。于栈的实现这里就不再赘述了,在前面的文章中已经详细的介绍过了。这里直接把前面实现过的栈的各种接口拷贝过来,包括用于定义队列的结构体:
typedef int STDataType;typedef struct Stack //表示栈
{STDataType* a;int top;int capacity;
}ST;//栈的部分
//初始化栈
void STInit(ST* ps)
{assert(ps);ps->a = (STDataType*)malloc(10 * sizeof(STDataType));assert(ps);ps->capacity = 10;ps->top = 0;
}
//判断栈是否为空
bool STEmpty(ST* ps)
{assert(ps);if (ps->top){return 0;}else{return 1;}
}
//压栈
void STPush(ST* ps, STDataType x)
{assert(ps);if (ps->top == ps->capacity){STDataType* ptr = (STDataType*)realloc(ps->a, (ps->capacity + 10) * sizeof(STDataType));assert(ptr);ps->a = ptr;ps->capacity += 10;}ps->a[ps->top] = x;ps->top++;
}
//出栈
void STPop(ST* ps)
{assert(ps && STEmpty(ps) == 0);ps->top--;
}
//计算栈中元素个数
int STSize(ST* ps)
{assert(ps);return ps->top;
}
//访问栈顶元素
STDataType STTop(ST* ps)
{assert(ps && STEmpty(ps) == 0);return ps->a[ps->top - 1];
}
//销毁栈
void STDestroy(ST* ps)
{assert(ps);free(ps->a);ps->capacity = 0;ps->top = 0;ps->a = NULL;
}
队列的部分
有了栈的实现后,我们首先应该创建两个栈:pushst与popst,用于插入与移除元素。并将这两个栈存放到一个结构体中,方便管理:
typedef struct //表示实现队列的两个栈
{ST pushst;ST popst;
} MyQueue;
创建队列
创建队列时,可以直接为前面声明的用于存放两个栈的结构体类型MyQueue动态开辟一块空间,然后再分别复用STInit初始化其中的两个栈即可:
//创建队列
MyQueue* myQueueCreate()
{MyQueue* pmq = (MyQueue*)malloc(sizeof(MyQueue));assert(pmq);STInit(&pmq->pushst);STInit(&pmq->popst);return pmq;
}
判断队列是否为空
队列为空,即两个栈均为空。
所以我们直接复用判断栈是否为空函数STEmpty,当两个栈均为空,即两个函数的返回值均为真时,返回真,否则返回假:
//判断队列是否为空:若为空返回true,非空返回false
bool myQueueEmpty(MyQueue* obj)
{assert(obj);if (STEmpty(&obj->pushst) && STEmpty(&obj->popst))//当两个队列全为空即全为非0才为空,返回1;{return true;}else{return false;}
}
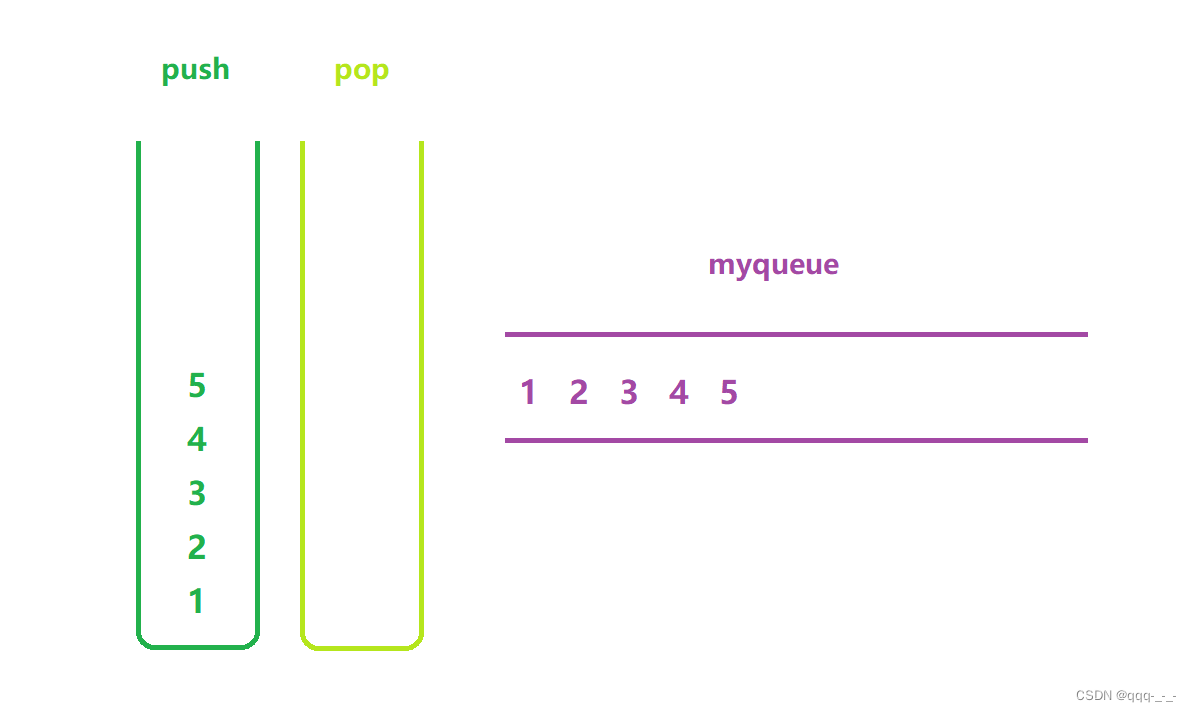
在队列尾入
任何时候插入元素时,在pushst栈中插入即可:
//在队列尾入
void myQueuePush(MyQueue* obj, int x)
{assert(obj);STPush(&obj->pushst, x);
}
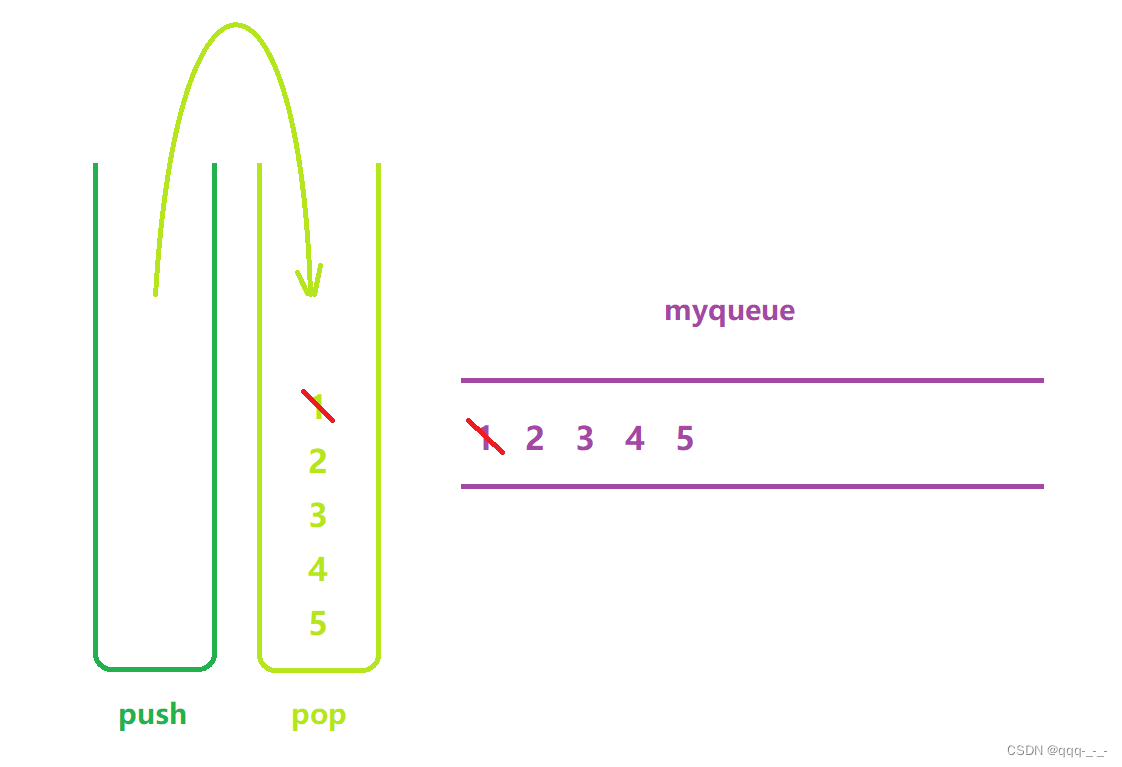
在队列头出
在队列头出时,永远从popst的栈顶移除即可,移除栈顶的元素时,复用STPop函数即可;
但是当popst为空时,就需要将pushst栈中的元素全部依次移动到popst栈中,我们可以通过复用STPush与STTop函数,将pushst栈顶的元素插入到popst中,然后再STPop移除pushst栈顶的元素即可。然后再pop掉popst的栈顶元素:
//从队列头出
int myQueuePop(MyQueue* obj)
{assert(obj && myQueueEmpty(obj) == 0);STDataType ret = 0;if (STEmpty(&obj->popst))//当pop栈为空时,才将push栈中的元素转移过去{while (STEmpty(&obj->pushst) == 0){STPush(&obj->popst, STTop(&obj->pushst));STPop(&obj->pushst);}}ret = STTop(&obj->popst);STPop(&obj->popst);return ret;
}
访问队头元素
访问队头元素时只需要复用STTop函数,访问popst栈顶的元素即可;
但是当popst栈为空时,就需要将pushst中的元素全部倒过去后再访问:
//返回队列开头的元素
int myQueuePeek(MyQueue* obj)
{assert(obj && myQueueEmpty(obj) == 0);//当pop为空时,只能转移后访问它;pop非空时可以直接访问pop的栈顶元素if (STEmpty(&obj->popst)){while (STEmpty(&obj->pushst) == 0){STPush(&obj->popst, STTop(&obj->pushst));STPop(&obj->pushst);}}return STTop(&obj->popst);
}
释放队列
释放队列时,分别释放两个栈即可。
当然,动态开辟的MyQueue型结构体也需要被释放:
//释放队列
void myQueueFree(MyQueue* obj)
{STDestroy(&obj->pushst);STDestroy(&obj->popst);free(obj);
}
总结
到此,关于用两个栈实现队列的题目就介绍完了,相信通过这两道题目,大家对于栈与队列的结构都有了更好的理解
下一篇文章中将会介绍循环队列的实现,欢迎大家持续关注哦
如果大家认为我对某一部分没有介绍清楚或者某一部分出了问题,欢迎大家在评论区提出
如果本文对你有帮助,希望一键三连哦
希望与大家共同进步哦
相关文章:

用栈实现队列(图示超详解哦)
全文目录引言用栈实现队列题目介绍思路简述实现栈的部分队列的部分创建队列判断队列是否为空在队列尾入在队列头出访问队头元素释放队列总结引言 在上一篇文章中,我们了解了用两个队列实现栈。在这篇问章中将继续介绍用两个栈实现队列的OJ练习: 用栈实现…...

Spring - Spring 注解相关面试题总结
文章目录01. Spring 配置方式有几种?02. Spring 如何实现基于xml的配置方式?03. Spring 如何实现基于注解的配置?04. Spring 如何基于注解配置bean的作用范围?05. Spring Component, Controller, Repository, Service 注解有何区别…...
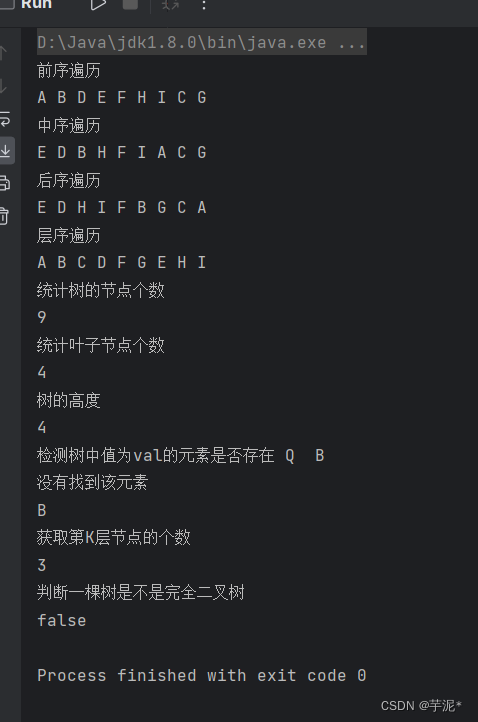
【数据结构】实现二叉树的基本操作
目录 1. 二叉树的基本操作 2. 具体实现 2.1 创建BinaryTree类以及简单创建一棵树 2.2 前序遍历 2.3 中序遍历 2.4 后序遍历 2.5 层序遍历 2.6 获取树中节点的个数 2.7 获取叶子节点的个数 2.8 获取第K层节点的个数 2.9 获取二叉树的高度 2.10 检测值为val的元素是否…...
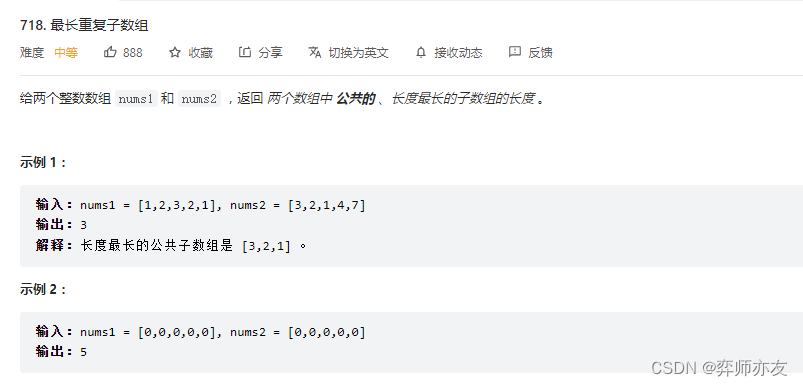
代码随想录算法训练营第五十二天| ● 300.最长递增子序列 ● 674. 最长连续递增序列 ● 718. 最长重复子数组
300.最长递增子序列 看完题后的思路 dp[i] [0,i]子数组中,以nums[i]结尾的子序列的长度 dp[i]dp[j]1 j从i-1向0遍历,在所有nums[j]<nums[i]中dp[j]最大 初始化 dp[0]1 代码 class Solution {public int lengthOfLIS(int[] nums) {if (nums.length0){return 0;}int[] dpne…...

手机验证发送及其验证(基于springboot+redis)保姆级
在Java开发中,发送手机验证码时需要考虑以下几个问题: 验证码的有效期:验证码应该有一定的有效期,一般设置为几分钟或者十几分钟。过期的验证码应该被认为是无效的,不能用于验证用户身份。手机号码格式的校验…...

【JavaScript 逆向】数美滑块逆向分析
声明本文章中所有内容仅供学习交流,相关链接做了脱敏处理,若有侵权,请联系我立即删除!案例目标验证码:aHR0cHM6Ly93d3cuaXNodW1laS5jb20vbmV3L3Byb2R1Y3QvdHcvY29kZQ以上均做了脱敏处理,Base64 编码及解码方…...

多任务之线程
文章目录一、多任务是什么?二、多任务-线程四、通过继承Tread类完成创建线程五、资源竞争六、同步与互斥锁七、对峙与避免死锁一、多任务是什么? 多个函数同时执行一件事情就是多任务,没有多任务的时候任务执行都是按照顺序的,而…...
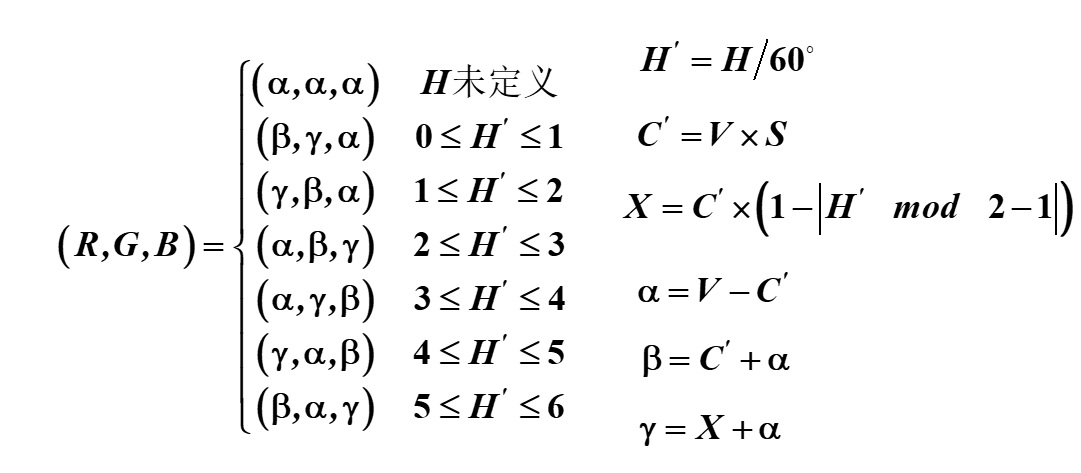
(数字图像处理MATLAB+Python)第二章数字图像处理基础-第二节:色度学基础与颜色模型
文章目录一:颜色匹配二:CIE 1931-RGB系统三:CIE 1931标准色度系统四:CIE 1976Lab均匀颜色空间五:孟塞尔表色系统(1)孟塞尔明度(Value,记为V)(2)孟塞尔彩度(Ch…...
)
【华为OD机试 2023最新 】 网上商城优惠活动(C++)
文章目录 题目描述输入描述输出描述备注用例题目解析C++题目描述 某网上商场举办优惠活动,发布了满减、打折、无门槛3种优惠券,分别为: 每满100元优惠10元,无使用数限制,如100199元可以使用1张减10元,200299可使用2张减20元,以此类推;92折券,1次限使用1张,如100元,…...

记一次CentOS 8 部署packstack部署OpenStack失败案例,请直接看最后
首先你需要一台安装好CentOS8 的虚拟机,相关参数如图。两块网卡,网卡1 NAT IP 192.168.100.100 GW192.168.100.2 网卡2 可不做配置。能ping通百度。创建完成虚拟机记得打好快照。 开机编辑基本配置环境变量 [rootlocalhost ~]# nmcli connection show NA…...

【2023春招】美团技术岗笔试10min+AK
随手投递了前端&移动端,笔试2道算法+选择+行测题(为什么笔试会有行测题?) 目录 T1-火车栈结构 题意 输入描述 输出描述 样例 AC_Code T2-春游...

Echarts实现图表自适应屏幕分辨率
一:简介 之前做项目的时候要实现echarts图表随浏览器窗口大小变化而改变,echarts本身提供了一个resize()方法,然后我们需要用一个函数实现浏览器窗口监听,最初我选用的是window.onresize方法,当页面只有一个图表时可以…...

【2023年第十一届泰迪杯数据挖掘挑战赛】B题:产品订单的数据分析与需求预测 建模及python代码详解 问题一
相关链接 【2023年第十一届泰迪杯数据挖掘挑战赛】B题:产品订单的数据分析与需求预测 建模及python代码详解 问题一 【2023年第十一届泰迪杯数据挖掘挑战赛】B题:产品订单的数据分析与需求预测 建模及python代码详解 问题二 1 题目 一.问题…...

【蓝桥杯嵌入式】第十三届蓝桥杯嵌入式国赛客观题以及详细题解
题1 概念题。 USRAT:异步串口通信,常用于数据传输;SW-DP:SWD 的全称应该是 The Serial Wire Debug Port (SW-DP),也就是串行调试端口,是 >ARM 目前支持的两种调试端口之一;JTAG-DP:另一个调试…...

java中Map遍历的4种方式
目录 1、map.entrySet()方式 2、map.keySet()方式 3、map.values()方式 4、forEach方式 本文以如下map案例: Map<String, String> map new HashMap<>(); map.put("student1", "张三"); map.put("student2", "…...
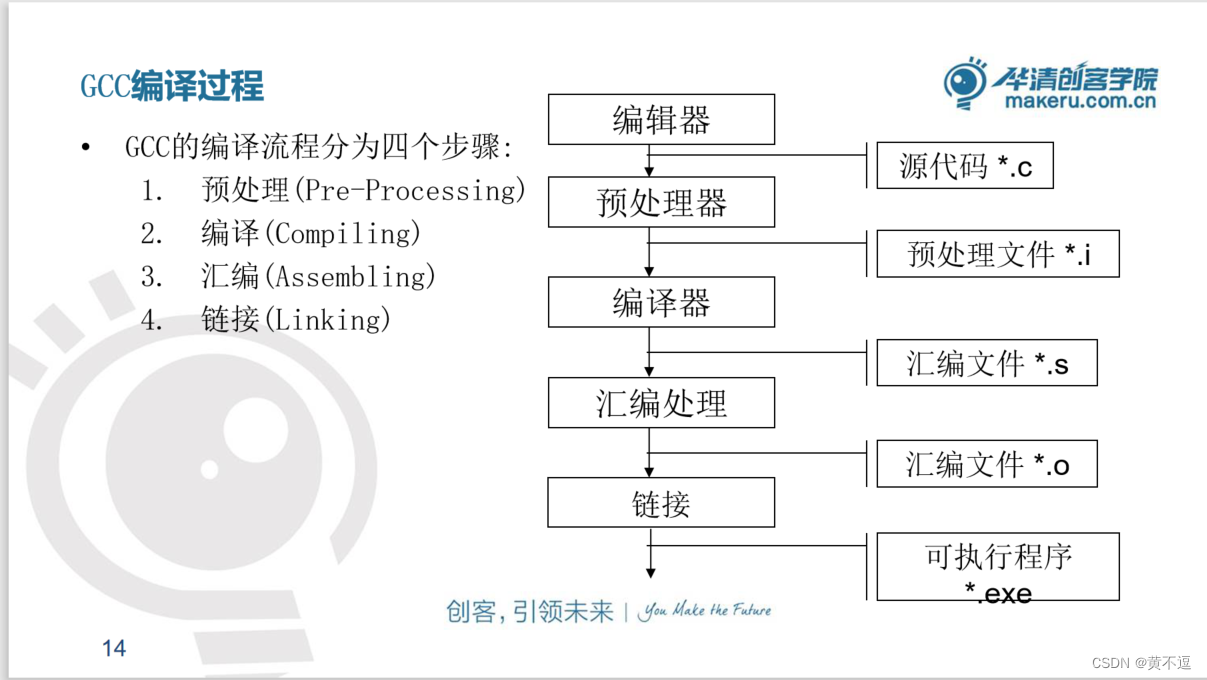
GCC 编译器的主要组件和编译过程
主要组件: 分析器:分析器将源语言程序代码转换为汇编语言。因为要从一种格式转换为另一种格式(C到汇编),所以分析器需要知道目标机器的汇编语言。 汇编器:汇编器将汇编语言代码转换为CPU可以执行字节码。 …...

蓝桥杯冲刺 - week2
文章目录💬前言🌲day1最大和 (DP质因数分解)901. 滑雪 - 记忆化搜索🌲day21227. 分巧克力 - 二分🌲day31221. 四平方和 - 空间换时间1230. K倍区间🌲day41076. 迷宫问题 - 路径2017-迷宫-填空🌲day5848. 有…...
第十四届蓝桥杯三月真题刷题训练——第 20 天
目录 第 1 题:纸张尺寸 问题描述 输入格式 输出格式 样例输入1 样例输出1 样例输入 2 样例输出 2 运行限制 代码: 解析: 第 2 题:最大数字 第 3 题:全排列的价值_递推公式 问题描述 输入格式 输出格式…...
【C++】科普:C++中的浮点数怎么在计算机中表示?
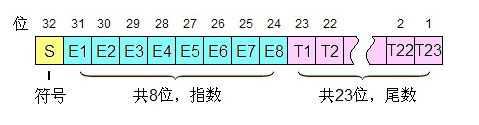
这里我们以8.25这个数为例说明计算机时如何存取float类型的数据的: float a 8.25;引言 1. 所占位数 首先,明确一个概念,float类型的数据在常规计算机中通常占4个字节,也就是32位。其内存分布如图: 位字段说明所占位…...

Linux 多线程:多线程和多进程的对比
目录一、多进程优缺点二、多线程优缺点三、使用多执行流的场景在多任务处理中,我们既可以使用多进程,也可以使用多线程。但多进程和多线程并不是随意选择的,因为它们应对的场景不同,优缺点也不同。 一、多进程优缺点 多进程就是在…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
