【动态规划算法题记录】最长/最大 问题汇总 (leetcode)
目录
- 32. 最长有效括号
- 思路
- 代码
- 300. 最长递增子序列
- 思路
- 代码
- 674. 最长连续递增序列
- 思路1:双指针
- 代码1:双指针
- 思路2:dp
- 代码2:dp
- 718. 最长重复子数组
- 思路1:dp
- 代码1:dp
- 思路2:dp优化
- 代码2:dp优化
- 1143. 最长公共子序列
- 思路
- 代码
- 1035. 不相交的线(最大连线数)
- 思路
- 代码
- 53. 最大子序和
- 思路1:贪心
- 代码1:贪心
- 思路2:dp
- 代码2:dp
32. 最长有效括号
题目🔗
给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
示例 1:
输入:s = "(()"
输出:2
解释:最长有效括号子串是 "()"
示例 2:
输入:s = ")()())"
输出:4
解释:最长有效括号子串是 "()()"
示例 3:
输入:s = ""
输出:0
思路
首先,我们定义一个dp数组,表示以第i个元素结尾的字符串的最长有效括号的长度。
对于dp[i]来说,它可能有以下两种情况:
s[i] == '(':这时他是无法和前面的括号组成有效括号对的,所以dp[i] = 0。s[i] == ')':这时我们需要确定它是否能和前面的元素组成有效括号对,那么还需要去观察s[i-1]:s[i-1] == '(':s[i-1]刚好和s[i]组成一对有效括号,长度为2。那么这种情况下我们可以推导出: d p [ i ] = d p [ i − 2 ] + 2 dp[i] = dp[i-2] + 2 dp[i]=dp[i−2]+2s[i-1] == ')':对于这种情况来说,我们不知道s[i-1]是否和前面的元素组成有效括号,但无论如何,dp[i-1]中存放的总是以s[i-1]结尾的字符串的最长有效括号长度。假设s[i-1]是有效的括号对之一,那么与他配对的括号index就是i-dp[i-1],于是乎我们就可以找到和s[i]配对的位置i-dp[i-1]-1,这样如果s[i-dp[i-1]-1] == '(',那么s[i]就能与他配对上。那么我们就可以推导出: d p [ i ] = d p [ i − 1 ] + 2 + d p [ i − d p [ i − 1 ] − 2 ] dp[i] = dp[i-1] + 2 + dp[i-dp[i-1]-2] dp[i]=dp[i−1]+2+dp[i−dp[i−1]−2]
注意,上面要需要加上 d p [ i − d p [ i − 1 ] − 2 ] dp[i-dp[i-1]-2] dp[i−dp[i−1]−2],这是因为如果我们判定s[i-dp[i-1]-1] == '('与s[i]配对的话,还需要考虑s[i-dp[i-1]-1]之前的情况。
代码
class Solution {
public:int longestValidParentheses(string s) {vector<int> dp(s.size(), 0);int ans = 0;for(int i = 1; i < s.size(); ++i){if(s[i] == ')'){// 前面一个是(的情况,直接配对成功if(s[i - 1] == '('){dp[i] = 2;// 加上前面配对的数量if(i - 2 >= 0) dp[i] += dp[i - 2];}// 前面一个也是),但是有配对的else if(dp[i - 1] > 0){// 判断匹配位置的符号是不是(,如果是则可以配对if((i - dp[i - 1] - 1) >= 0 && s[i - dp[i - 1] - 1] == '('){dp[i] = dp[i - 1] + 2;// 加上前面配对的数量if(i - dp[i - 1] - 2 >= 0) dp[i] += dp[i - dp[i - 1] - 2];}}}ans = max(ans, dp[i]);}return ans;}
};
300. 最长递增子序列
题目🔗
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
输入:nums = [0,1,0,3,2,3]
输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7]
输出:1
思路
dp[i]表示第i个数为结尾的子序列的最长严格递增长度。
很容易的就能想到,我们要计算的dp[i]一共有两种情况:
- nums[i] > nums[i - 1]:此时dp[i] = dp[i-1] + 1
- nums[i] < nums[i - 1]:此时dp[i] = dp[i-1]
但是如果我们简单的将代码写成这样:
int lengthOfLIS(vector<int>& nums) {vector<int> dp(nums.size(), 1);for(int i = 1; i < nums.size(); ++i){if(nums[i] > nums[i - 1])dp[i] = dp[i - 1] + 1;else dp[i] = dp[i-1];}return dp[nums.size()-1];}
当测试用例为:nums = [4,10,4,3,8,9]。我们打印出上面代码计算出的dp数组:1 2 2 2 3 4 。可以发现并不是我们所期望的那样,当i=4时,dp[4]应该为2,而不是3。
我们计算成3是因为:对于子数组[4,10,4,3]来说,它的最大递增子序列为4, 10。我们如果只是简单的判断nums[4] > nums[3],就执行dp[i] = dp[i - 1] + 1,那么就相当于是把4, 10, 8当成了最大递增子序列,然而它并不是的,所以这里就出现了判断失误。
正确的做法是,我们要把dp[i]定义为第i个数为结尾的子数组的最长严格递增长度,并且该最长严格递增子序列最后一个数必定是nums[i]。
每次进行判断的时候,我们要对该子数组各个位置nums[j]进行遍历,并比较与nums[i]的大小,如果nums[i] > nums[j],那么就有dp[i] = max(dp[i], dp[j] + 1)。
最终答案就是dp数组中最大的那个数。
代码
class Solution {
public:int lengthOfLIS(vector<int>& nums) {vector<int> dp(nums.size(), 1);int ans = 1;for(int i = 1; i < nums.size(); ++i){for(int j = 0; j < i; ++j){if(nums[i] > nums[j])dp[i] = max(dp[i], dp[j] + 1);}ans = max(ans, dp[i]);}return ans;}
};
674. 最长连续递增序列
题目🔗
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
示例 1:
输入:nums = [1,3,5,4,7]
输出:3
解释:最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
示例 2:
输入:nums = [2,2,2,2,2]
输出:1
解释:最长连续递增序列是 [2], 长度为1。
思路1:双指针
定义两个指针:int slow和int fast。
代码1:双指针
class Solution {
public:int findLengthOfLCIS(vector<int>& nums) {int slow = 0;int ans = 0;while(slow < nums.size()){int fast = slow + 1;while(fast < nums.size() && nums[fast] > nums[fast - 1]){fast++;}ans = max(ans, fast - slow);slow = fast;}return ans;}
};
思路2:dp
dp的思路和上题类似。我们定义一个dp数组,dp[i]表示第i个数为结尾的子数组的最长连续递增长度,并且该最长连续递增序列最后一个数必定是nums[i]。
与上题不一样的就是我们不在需要遍历子数组了,直接判断nums[i]和nums[i - 1]的大小即可。
代码2:dp
class Solution {
public:int findLengthOfLCIS(vector<int>& nums) {vector<int> dp(nums.size(), 1);int ans = 1;for(int i = 1; i < nums.size(); ++i){if(nums[i] > nums[i - 1]){dp[i] = max(dp[i], dp[i - 1] + 1);}ans = max(ans, dp[i]);}return ans;}
};
718. 最长重复子数组
题目🔗
给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。
示例 1:
输入:nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出:3
解释:长度最长的公共子数组是 [3,2,1] 。
示例 2:
输入:nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
输出:5
思路1:dp
dp[i][j]表示数组nums1前i个元素和数组nums2前j个元素的最长公共子数组的长度。其实也是和上题一样的。
代码1:dp
我们可以很快写出代码:
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>> dp(nums1.size(), vector<int>(nums2.size(), 0));int ans = 0;// dp数组初始化for(int i = 0; i < nums1.size(); ++i){if(nums2[0] == nums1[i]) dp[i][0] = 1;if(dp[i][0] > ans) ans = dp[i][0];}for(int j = 0; j < nums2.size(); ++j){if(nums1[0] == nums2[j]) dp[0][j] = 1;if(dp[0][j] > ans) ans = dp[0][j];}// dp数组推导for(int i = 1; i < nums1.size(); ++i){for(int j = 1; j < nums2.size(); ++j){if(nums1[i] == nums2[j])dp[i][j] = dp[i - 1][j - 1] + 1;if(dp[i][j] > ans) ans = dp[i][j];}}return ans;}
};
注意初始化的时候我们也要去更新ans的大小,不然会漏结果。
思路2:dp优化
其实,我们可以将dp[i][j]定义为数组nums1前i-1个元素和数组nums2前j-1个元素的最长公共子数组的长度,也就是在nums1前增加一行,nums2前增加一列:

这样我们在定义数组的时候就已经初始化好了,不必额外去for循环初始化:vector<vector<int>> dp (nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
代码2:dp优化
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));int ans = 0;// dp数组推导for(int i = 1; i <= nums1.size(); ++i){for(int j = 1; j <= nums2.size(); ++j){if(nums1[i - 1] == nums2[j - 1])dp[i][j] = dp[i - 1][j - 1] + 1;if(dp[i][j] > ans) ans = dp[i][j];}}return ans;}
};
1143. 最长公共子序列
题目🔗
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1:
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3 。
示例 2:
输入:text1 = "abc", text2 = "abc"
输出:3
解释:最长公共子序列是 "abc" ,它的长度为 3 。
示例 3:
输入:text1 = "abc", text2 = "def"
输出:0
解释:两个字符串没有公共子序列,返回 0 。
思路
这题和上题的不同之处在于 公共子序列和原字符串是相对有序的。感觉这题有点像300. 最长递增子序列和718. 最长重复子数组的结合体。
上一题以i-1和j-1是因为子数组必须要求是连续的,如果不连续,公共子数组直接归零,下一个子数组不能继承前一个子数组的公共子数组长度。
子序列则不一样,允许中间有间隔,下一个子序列可以继承前一个子序列的公共子序列长度。
这样说很抽象,我们举个例子。比如说两个数组nums1 = [1,2,3,4,5], nums2 = [1,2,3,8,5] 。在index=3的时候出现分歧了,如果是公共子数组,到index=3时,其公共子数组必须要归零,如果不归零,会影响index=4的判断。而如果是公共子序列,index=3可以保留index=2的最长子序列数,继而在index=4时继续递增。
代码
class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int len1 = text1.size();int len2 = text2.size();vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1, 0));for(int i = 1; i <= len1; ++i){for(int j = 1; j <= len2; ++j){if(text1[i - 1] == text2[j - 1]){dp[i][j] = dp[i - 1][j - 1] + 1;}else{dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[len1][len2];}
};
1035. 不相交的线(最大连线数)
题目🔗
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足:
nums1[i] == nums2[j]- 且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
示例 1:

输入:nums1 = [1,4,2], nums2 = [1,2,4]
输出:2
解释:可以画出两条不交叉的线,如上图所示。 但无法画出第三条不相交的直线,因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。
示例 2:
输入:nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出:3
示例 3:
输入:nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
输出:2
思路
和1143. 最长公共子序列一模一样。
代码
class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {int len1 = nums1.size();int len2 = nums2.size();vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1, 0));for(int i = 1; i <= len1; ++i){for(int j = 1; j <= len2; ++j){if(nums1[i - 1] == nums2[j - 1]){dp[i][j] = dp[i - 1][j - 1] + 1;}else{dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[len1][len2];}
};
53. 最大子序和
题目🔗
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
思路1:贪心
因为数组中包含负数,所以会拉低连续子数组的和,甚至变为负数,这个时候就说明从前面计算到这里的负数,再继续计算下去肯定只会越来越小,所以我们要放弃前面的元素,从下一个元素开始重新计算。每次计算的时候我们都要记录更大的连续和,最后得到的就是全局最优的最大连续和。
代码1:贪心
class Solution {
public:int maxSubArray(vector<int>& nums) {int result = INT32_MIN;int count = 0;for(int i = 0; i < nums.size(); i++) {count += nums[i];if(count > result) result = count;if(count <= 0) count = 0;}return result;}
};
思路2:dp
dp[i]表示以nums[i-1]为结尾的最大子数组的和为dp[i]。
对于每个dp[i]都有两种情况:
nums[i-1]加入到前面的子数组中,也就是dp[i] = dp[i - 1] + nums[i - 1]nums[i-1]不加入到前面的子数组中,从它这里重新开始计算和,也就是dp[i] = numd[i - 1]- 我们取最大的值:
dp[i] = max(nums[i - 1], dp[i - 1] + nums[i - 1])
代码2:dp
class Solution {
public:int maxSubArray(vector<int>& nums) {vector<int> dp(nums.size() + 1, 0);int ans = INT_MIN;for(int i = 1; i <= nums.size(); ++i){dp[i] = max(nums[i - 1], dp[i - 1] + nums[i - 1]);if(dp[i] > ans) ans = dp[i];}return ans;}
};
相关文章:

【动态规划算法题记录】最长/最大 问题汇总 (leetcode)
目录 32. 最长有效括号思路代码 300. 最长递增子序列思路代码 674. 最长连续递增序列思路1:双指针代码1:双指针思路2:dp代码2:dp 718. 最长重复子数组思路1:dp代码1:dp思路2:dp优化代码2&#x…...

2020 位示图
2020年网络规划设计师上午真题解析36-40_哔哩哔哩_bilibili 假设某计算机的字长为32位,该计算机文件管理系统磁盘空间管理采用位示图(bitmap),记录磁盘的使用情况。若磁盘的容量为300GB,物理块的大小为4MB,…...

富格林:防止陷入黑幕欺诈平台
富格林指出,不少投资者因未做好投资准备而不慎误入黑幕欺诈平台,造成了不必要的亏损。投资者在投资前,需要时刻保持警惕,根据市场行情,作出有依据的投资决定,而不是依赖黑幕欺诈平台的噱头进行投资。建议投…...

Cookie、Session 、token
Cookie 优点: 简单易用: 浏览器自动管理 Cookie 的发送和接收。持久性: 可以设置过期时间,使其可以在浏览器关闭后依旧存在。广泛支持: 所有现代浏览器都支持 Cookie。 缺点: 安全性问题: 存储在客户端,容易被查看和篡改。敏感信息不应直接存储在 Co…...

Json-类型映射使用TypeFactory或者TypeReference
当你需要将JSON数据转换为Java中的复杂类型时,可以使用Jackson库中的TypeFactory或 者TypeReference。这两种方式可以帮助你处理复杂的泛型类型,例如 List<Map<String, Object>> 或者 Map<String, List<Object>>。 示例 1: 使用 TypeFactory 和 T…...
Linux shell编程学习笔记73:sed命令——沧海横流任我行(上)
0 前言 在大数据时代,我们要面对大量数据,有时需要对数据进行替换、删除、新增、选取等特定工作。 在Linux中提供很多数据处理命令,如果我们要以行为单位进行数据处理,可以使用sed。 1 sed 的帮助信息,功能ÿ…...

内网渗透之icmp隧道传输
原理 # 为什么要建立隧道 在实际的网络中,通常会通过各种边界设备软/硬件防火墙、入侵检测系统来检查对外连接的情况,如果发现异常,会对通信进行阻断。 # 什么是隧道 就是一种绕过端口屏蔽的方式,防火墙两端的数据包通过防火墙…...

【C++ 第十五章】map 和 set 的封装(封装红黑树)
1. map 和 set 的介绍 ⭐map 与 set 分别是STL中的两种序列式容器; 它们是一种树形数据结构的容器,且其的底层构造为一棵红黑树; 而在上一篇文章中提到,其实红黑树本身就是一棵二叉搜索树,是基于二叉搜索树的性质对其增加了平衡的属性来提高其综合性能 ⭐当然也…...

LIN通讯
目录 1 PLinApi.h 2 TLINFrameEntry 结构体 3 自定义函数getTLINFrameEntry 4 TLINScheduleSlot 结构体 5 自定义函数 getTLINScheduleSlot 6 自定义LIN_SetScheduleInit函数 7 自定义 LIN_StartSchedule 8 发送函数 9 线程接收函数 1 PLinApi.h 这是官方头文件 ///…...
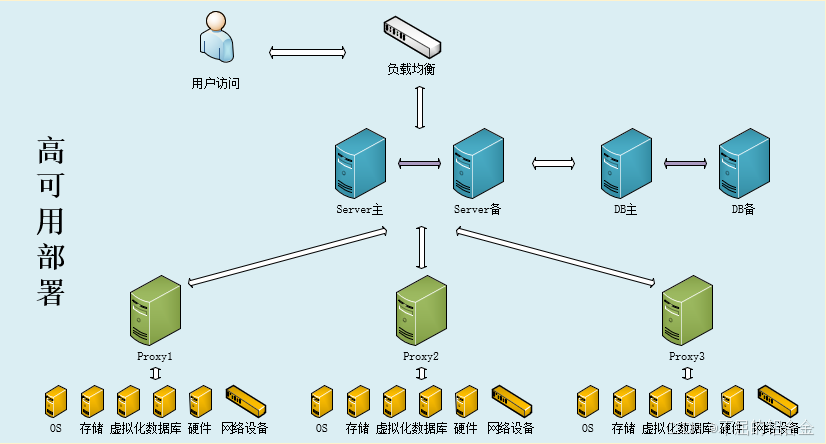
zabbix常见架构及组件
Zabbix作为一个开源的、功能全面的监控解决方案,广泛应用于各类组织中,以实现对网络、服务器、云服务及应用程序性能的全方位监控。部署架构灵活性高,可支持从小型单一服务器环境到大型分布式系统的多种场景。基本架构通常包括监控端…...
plsql表格怎么显示中文 plsql如何导入表格数据
在Oracle数据库开发中,PL/SQL Developer是一款广泛使用的集成开发环境(IDE),它提供了丰富的功能来帮助开发人员高效地进行数据库开发和管理。在使用PL/SQL Developer时,许多用户会遇到表格显示中文的问题,以…...

chromedriver下载地址大全(包括124.*后)以及替换exe后仍显示版本不匹配的问题
Chrome for Testing availability CNPM Binaries Mirror 若已经更新了系统环境变量里的chromdriver路径下的exe,仍显示版本不匹配: 则在cmd界面输入 chromedriver 会跳出version verison与刚刚下载好的exe不匹配,则再输入: w…...

拦截器实现 Mybatis Plus 打印含参数的 SQL 语句
1.实现拦截器 package com.sample.common.interceptor;import com.baomidou.mybatisplus.extension.plugins.inner.InnerInterceptor; import lombok.extern.slf4j.Slf4j; import org.apache.ibatis.executor.Executor; import org.apache.ibatis.mapping.BoundSql; import or…...

Oracle Subprogram即Oracle子程序
Oracle Subprogram,即Oracle子程序,是Oracle数据库中存储的过程(Procedures)和函数(Functions)的统称。这些子程序是存储在数据库中的PL/SQL代码块,用于执行特定的任务或操作。下面详细介绍Orac…...

自然语言处理实战项目30-基于RoBERTa模型的高精度的评论文本分类实战,详细代码复现可直接运行
大家好,我是微学AI,今天给大家介绍一下自然语言处理实战项目30-基于RoBERTa模型的高精度的评论文本分类实战,详细代码复现可直接运行。RoBERTa模型是由 Facebook AI Research 和 FAIR 的研究人员提出的一种改进版的 BERT 模型。RoBERTa 通过采用更大的训练数据集、动态掩码机…...
RK3588J正式发布Ubuntu桌面系统,丝滑又便捷!
本文主要介绍瑞芯微RK3588J的Ubuntu系统桌面演示,开发环境如下: U-Boot:U-Boot-2017.09 Kernel:Linux-5.10.160 Ubuntu:Ubuntu20.04.6 LinuxSDK: rk3588-linux5.10-sdk-[版本号] (基于rk3…...
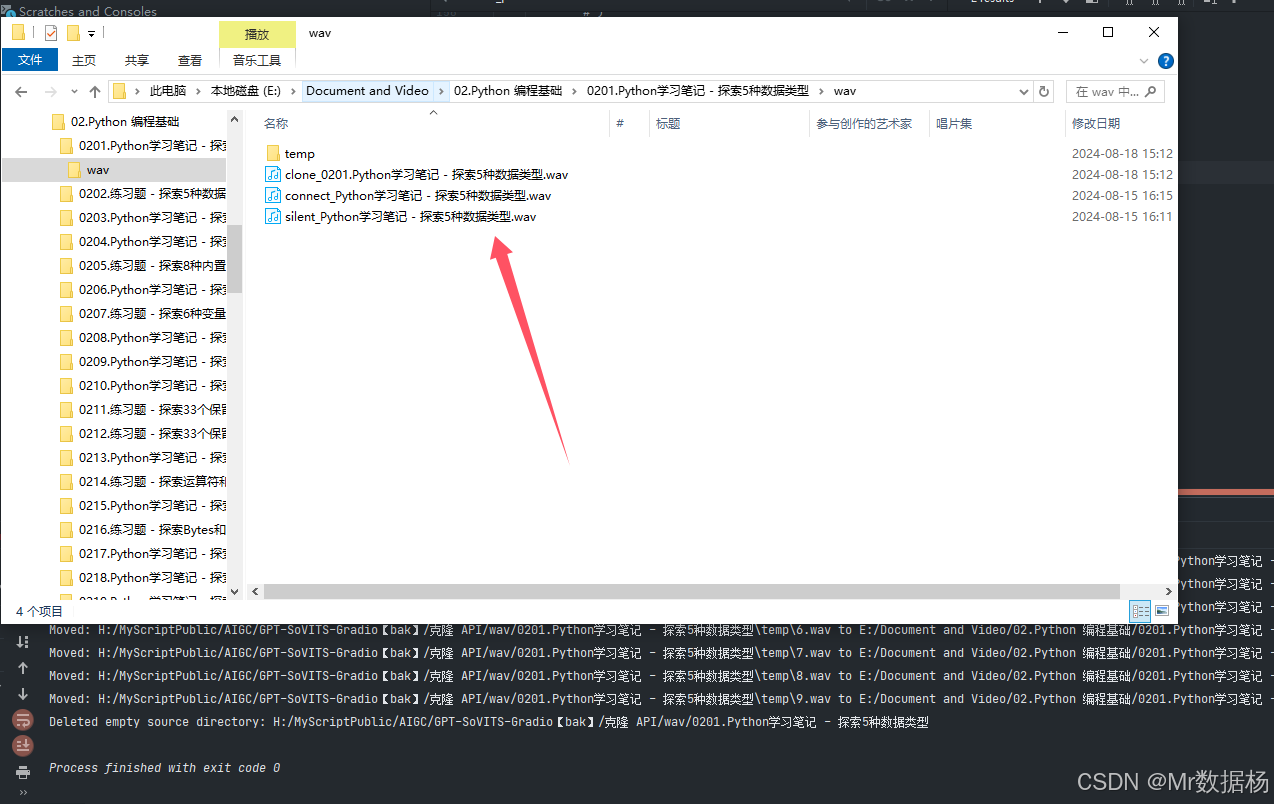
基于GPT-SoVITS的API实现批量克隆声音
目标是将每一段声音通过GPT-SoVITS的API的API进行克隆,因为拼在一起的整个片段处理会造成内存或者缓存溢出。 将目录下的音频文件生成到指定目录下,然后再进行拼接。 通过AI工具箱生成的数据文件是这样的结构,temp目录下是没个片段生成的部分,connect_是正常拼接的音频文件…...
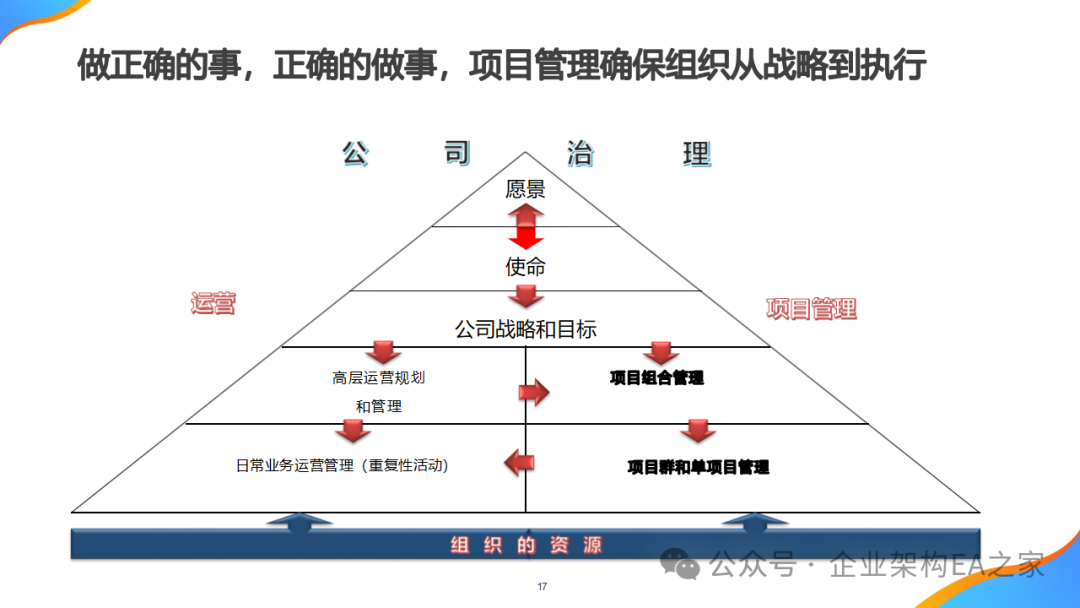
详解华为项目管理,附华为高级项目管理内训材料
(一)华为在项目管理中通过有效的沟通、灵活的组织结构、坚持不懈的努力、细致的管理和科学的考核体系,实现了持续的创新和发展。通过引进先进的管理模式,强调以客户需求为导向,华为不仅优化了技术管理和项目研发流程&a…...
脚本)
Perl(Practical Extraction and Reporting Language)脚本
Perl(Practical Extraction and Reporting Language)是一种非常灵活的脚本语言,主要用于文本处理、系统管理以及快速原型开发等领域。Perl 脚本可以用来执行一系列任务,包括文件操作、网络通信、数据处理等。 下面是一些关于编写…...

单例模式详细
文章目录 单例模式介绍八种方式1、饿汉式(静态常量)2、饿汉式(静态代码块)3、懒汉式(线程不安全)4、懒汉式(线程安全,同步方法)5、懒汉式(线程不安全…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
