一元四次方程求解-【附MATLAB代码】
目录
前言
求解方法
编辑
MATLAB验证
附:一元四次方程的故事
前言
最近在研究机器人的干涉(碰撞)检测,遇到了一个问题,就是在求椭圆到原点的最短距离时,构建的方程是一个一元四次方程。无论是高中的初等数学,大学的高等数学,还是研究生的高等代数,都没有关于一元四次方程的求解方法,大多都是一元二次方程的求解。仔细一研究才知道为什么很少提及一元四次方程。具体解法如下:
求解方法






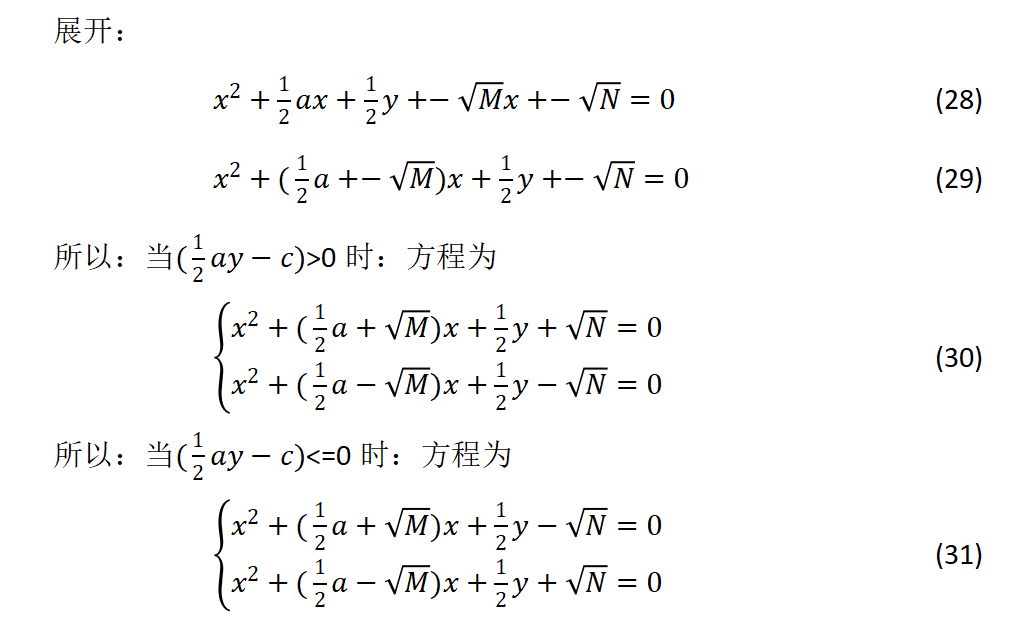

MATLAB验证
% output
% root:为方程的解(根),i 为解的个数
% input
% parameter 为方程的5个系数function [root,i] = MYSolve4OrderEquaton(parameter)
a=parameter(2)/parameter(1);
b=parameter(3)/parameter(1);
c=parameter(4)/parameter(1);
d=parameter(5)/parameter(1);a3=1;
b3=-b;
c3=(a*c-4*d);
d3=-(a^2*d-4*b*d+c^2);
parameter3=[a3,b3,c3,d3];
[root3,y3,i3] = Solve3OrderEquaton(parameter3);
i=0;
root=[];
for j=1:1if(a^2/4-b+root3(j)<0||root3(j)^2/4-d<0)break;endalpha=sqrt(a^2/4-b+root3(j));beta=sqrt(root3(j)^2/4-d);if(a*root3(j)/2-c>0)a21=1;b21=a/2-alpha;c21=root3(j)/2-beta;parameter21=[a21,b21,c21];[root21,y21,i21] = Solve2OrderEquaton(parameter21);a22=1;b22=a/2+alpha;c22=root3(j)/2+beta;parameter22=[a22,b22,c22];[root22,y22,i22] = Solve2OrderEquaton(parameter22);elsea21=1;b21=a/2-alpha;c21=root3(j)/2+beta;parameter21=[a21,b21,c21];[root21,y21,i21] = Solve2OrderEquaton(parameter21);a22=1;b22=a/2+alpha;c22=root3(j)/2-beta;parameter22=[a22,b22,c22];[root22,y22,i22] = Solve2OrderEquaton(parameter22);endroot4{j}=[root21,root22];i4{j}=[i21,i22];root=[root,root4{j}];i=i+i21+i22;
end
end
function [root,y,i] = Solve3OrderEquaton(parameter)
a=parameter(1);
b=parameter(2);
c=parameter(3);
d=parameter(4);
a_2=a*a;
a_3=a_2*a;
b_2=b*b;
b_3=b_2*b;
p=c/3/a-b_2/9/a_2;
q=d/2/a+b_3/27/a_3-b*c/6/a_2;
delta=q*q+p^3;
if(delta>0)i=1;root=nthroot(-q+sqrt(delta),3)+nthroot(-q-sqrt(delta),3)-b/3/a;
elseif(delta==0)i=2;root(1)=-2*nthroot(q,3)-b/3/a;root(2)=nthroot(q,3)-b/3/a;
elsei=3;alpha=1/3*acos(-q*sqrt(-p)/p^2);root(1)=2*sqrt(-p)*cos(alpha)-b/3/a;root(2)=2*sqrt(-p)*cos(alpha+2/3*pi)-b/3/a;root(3)=2*sqrt(-p)*cos(alpha+4/3*pi)-b/3/a;
end
y=a*root.^3+b*root.^2+c*root+d;
end
function [root,y,i] = Solve2OrderEquaton(parameter)
a=parameter(1);
b=parameter(2);
c=parameter(3);
delta=b^2-4*a*c;
if(delta>0)i=2;root(1)=(-b+sqrt(delta))/2/a;root(2)=(-b-sqrt(delta))/2/a;
elseif(delta==0)i=1;root=-b/2/a;
elsei=0;root=[];
end
y=a*root.^2+b*root+c;
end测试代码
clc;
clear;
parameter = [1,1,1,1,0];
[root,i]=MYSolve4OrderEquaton(parameter);
[root,i]结果验证

附:一元四次方程的故事
塔尔塔利亚是意大利人,出生于1500年。他12岁那年,被入侵的法国兵砍伤了头部和舌头,从此说话结结巴巴,人们就给他一个绰号“塔尔塔利亚”(在意大利语中,这是口吃的意思),真名反倒少有人叫了,他自学成才,成了数学家,宣布自己找到了三次方程的的解法。这时,意大利数学家卡丹出场,请求塔尔塔利把解方程的方法告诉他,可是遭到了拒绝。后来卡丹对塔尔塔利假装说要推荐他去当西班牙炮兵顾问,称自己因为无法解三次方程而内心痛苦并发誓永远不泄漏塔尔塔利亚解一元三次方程式的秘密。塔尔塔利亚这才把解一元三次方程的秘密告诉了卡丹。六年以后,卡丹不顾原来的信约,在他的著作《关于代数的大法》中,将经过改进的三次方程的解法公开发表。后人就把这个方法叫作卡丹公式,塔尔塔利亚的名字反而被湮没了。
卡当公布了塔塔利亚发现的一元三次方程求根公式之后,塔尔塔利亚谴责卡当背信弃义,提出要与卡当进行辩论与比赛。这场辩论与比赛在米兰市的教堂进行,代表卡当出场的是卡当的学生费拉里。
费拉里(Ferrari L.,1522~1565)出身贫苦,少年时代曾作为卡当的仆人。卡当的数学研究引起了他费拉里对数学的热爱,当其数学才能被卡当发现后,卡当就收他作了学生。
费拉里代替卡当与塔尔塔利亚辩论并比赛时,风华正茂,他不仅掌握了一元三次方程的解法,而且掌握了一元四次方程的解法,因而在辩论与比赛中取得了胜利,并由此当上了波伦亚大学的数学教授。
一元四次方程的求解方法,是受一元三次方程求解方法的启发而得到的。一元三次方程是在进行了一元二次方程从而得解的。于是,如果能够巧妙地把一元四次方程巧妙的换元之后,把问题归结成了转化为一元三次方程或一元二次方程,就可以利用己知的公式求解了。
不幸的是,就像塔尔塔利亚发现的一元三次方程求根公式被误称为卡当公式一样,费拉里发现的一元四次方程求解方法也曾被误认为是波培拉发现的。
相关文章:

一元四次方程求解-【附MATLAB代码】
目录 前言 求解方法 编辑 MATLAB验证 附:一元四次方程的故事 前言 最近在研究机器人的干涉(碰撞)检测,遇到了一个问题,就是在求椭圆到原点的最短距离时,构建的方程是一个一元四次方程。无论是高中的…...

【极限性能,尽在掌控】ROG NUC:游戏与创作的微型巨擘
初见ROG NUC,你或许会为它的小巧体型惊讶。然而,这看似不起眼的机身内,蕴藏着游戏、创意的强大能量。 掌中风暴,性能无界 ROG NUC搭载英特尔高性能处理器,配合高速NVMe SSD固态硬盘以及可选的高端独立显卡(…...

Ecosmos开启公测,将深度赋能CIOE中国光博会元宇宙参会新体验
如今,生成式AI技术的发展,极大地降低了3D数字资产的制作成本,元宇宙作为一种可以无缝将物理和数字资产进行融合的技术,在推动电子产业数字化进程、助力产业高质量发展的方面展现出了巨大的潜力。 当前,发展新质生产力是…...
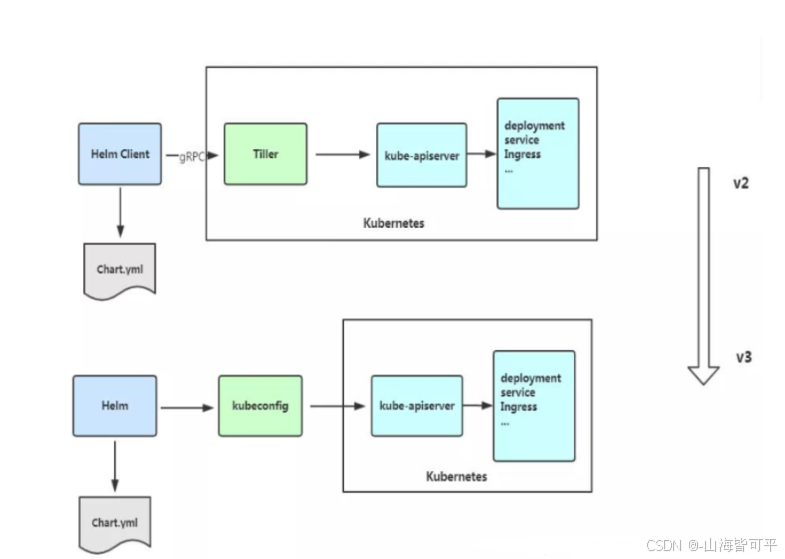
【Kubernetes】k8s集群之包管理器Helm
目录 一.Helm概述 1.Helm的简介 2.Helm的三个重要概念 3.Helm2与Helm3的的区别 二.Helm 部署 1.安装 helm 2.使用 helm 安装 Chart 3.Helm 自定义模板 4.Helm 仓库 每个成功的软件平台都有一个优秀的打包系统,比如Debian、Ubuntu 的 apt,RedH…...
)
嵌入式linux系统镜像制作day3(构建镜像)
点击上方"蓝字"关注我们 01、上节回顾 嵌入式linux系统镜像制作day1嵌入式linux系统镜像制作day2提前下载好准备工具,不然失败了大眼瞪小眼。 02、构建 Poky 的 Sato 镜像1 环境: ubuntu18.04poky版本:Dizzy 工具git 在开始之前,针对不同的发行版,需要先执行…...

【生日视频制作】教师节中秋节国庆节车模特美女举牌AE模板修改文字软件生成器教程特效素材【AE模板】
教师节中秋节国庆节车模特美女举牌生日视频制作教程AE模板改文字软件生成器素材 怎么如何做的【生日视频制作】教师节中秋节国庆节车模特美女举牌AE模板修改文字软件生成器教程特效素材【AE模板】 生日视频制作步骤: 安装AE软件下载AE模板把AE模板导入AE软件修改图…...
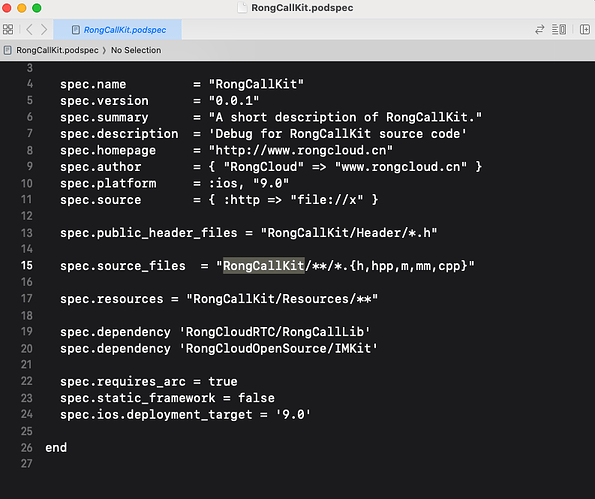
RongCallKit iOS 端本地私有 pod 方案
RongCallKit iOS 端本地私有 pod 方案 需求背景 适用于源码集成 CallKit 时,使用 pod 管理 RTC framework 以及源码。集成 CallKit 时,需要定制化修改 CallKit 的样式以及部分 UI 功能。适用于 CallKit 源码 Debug 调试便于定位相关问题。 解决方案 从…...

C++11:可变参数模板
目录 一、概述 二、场景 1.深拷贝的类 2.浅拷贝的类 C使用指南 一、概述 // Args是一个模板参数包,args是一个函数形参参数包 // 声明一个参数包Args...args,这个参数包中可以包含0到任意个模板参数。 template <class ...Args> void ShowList(…...

C++ 与 QML 之间进行数据交互的几种方法
https://www.cnblogs.com/jzcn/p/17774676.html 一、属性绑定 这是最简单的方式,可以在QML中直接绑定C 对象的属性。通过在C 对象中使用Q_PROPERTY宏定义属性,然后在QML中使用绑定语法将属性与QML元素关联起来。 1. person.h #include <QObject&g…...

Javaweb学习之Vue项目的创建(二)
学习资料 Vue.js - 渐进式 JavaScript 框架 | Vue.js (vuejs.org) 准备工作都做完了,接下来开始Vue的正式学习。 第一步,打开VS Code 在VS Code里,我们也需要使用到终端,如果不是以管理员身份打开,在新建Vue项目的时候…...

『深度长文』4种有效提高LLM输出质量的方法!
LLM,全称Large Language Model,意为大型语言模型,是一种基于深度学习的AI技术,能够生成、理解和处理自然语言文本,也因此成为当前大多数AI工具的核心引擎。LLM通过学习海量的文本数据,掌握了词汇、语法、语…...

【工业机器人】工业异常检测大模型AnomalyGPT
AnomalyGPT 工业异常检测视觉大模型AnomalyGPT AnomalyGPT: Detecting Industrial Anomalies using Large Vision-Language Models AnomalyGPT是一种基于大视觉语言模型(LVLM)的新型工业异常检测(IAD)方法。它利用LVLM的能力来理…...

【PGCCC】PostgreSQL案例:planning time超长问题分析#PG初级
在使用 PostgreSQL 时,查询的执行计划(planning time)有时会出现异常长的情况,这可能会影响数据库的整体性能。分析和解决这种问题可以从多个角度入手,以下是常见原因和相应的解决思路: 1. 统计信息不准确…...

【图文并茂】ant design pro 如何给后端发送 json web token - 请求拦截器的使用
上一节有讲过 【图文并茂】ant design pro 如何对接后端个人信息接口 还差一个东西,去获取个人信息的时候,是要发送 token 的,不然会报 403. 就是说在你登录之后才去获得个人信息。这样后端才能知道是谁的信息。 token 就代码了某个人。 …...

【微信小程序】自定义组件 - behaviors
1. 什么是 behaviors 2. behaviors 的工作方式 3. 创建 behavior 调用 Behavior(Object object) 方法即可创建一个共享的 behavior 实例对象,供所有的组件使用: 4. 导入并使用 behavior 5. behavior 中所有可用的节点 6. 同名字段的覆盖和组合规则* 关…...

Linux ubuntu 24.04 安装运行《帝国时代3》免安装绿色版游戏,解决 “Could not load DATAP.BAR”等问题
Linux ubuntu 24.04 安装运行《帝国时代3》游戏,解决 “Could not load DATAP.BAR" 等问题 《帝国时代 3》是一款比较经典的即时战斗游戏,伴随了我半个高中时代,周末有时间就去泡网吧,可惜玩的都是简单人机,高难…...

Springboot 图片
Springboot 图片 因为 server.servlet.context-path: /api 所以 url是这个的时候 http://127.0.0.1:9100/api/staticfiles/image/dd56a59d-da84-441a-8dac-1d97f9e42090.jpeg 配置代码的前面的 /api 是不要写的 package com.gk.study.config;import org.springframework.conte…...

LIMS实验室管理系统如何实现数据自动采集
随着科研技术的不断发展,LIMS实验室管理系统的应用也愈来愈广,已经成为现代化实验室管理不可或缺的工具。LIMS实验室管理系统未与仪器设备对接前,仪器设备产生的数据都是通过人工录入到系统中,再经过人工审核形成最终的数据报告。…...

全自动商用油炸锅介绍:
全自动商用油炸锅是一种专门为商业用途设计的厨房设备,旨在高效、节能、卫生地完成大量食品的油炸加工。这种设备通常采用油水混合技术,能够自动过滤残渣,延长换油周期,从而大大降低用油成本。全自动商用油炸锅适合中、小型油炸…...

CE修改器的简单使用
前言 这个系列目前是出于兴趣爱好,最终目的是为了可以用代码控制修改单机游戏。 这篇文章的对象是《植物大战僵尸杂交版》,其余游戏类似。 博客仅做技术研究使用,禁止用作商业用途。 1,安装CE修改器 到官网进行下载ÿ…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...

