Day 21代码|随想录| 二叉树完结撒花,今日刷题669.修剪二叉搜索树、108.将有序数组转换为二叉搜索树、538.吧二叉搜索树转换为累加树
提示:DDU,供自己复习使用。欢迎大家前来讨论~
文章目录
- 二叉树 Part06
- 二、题目
- 题目一:669.修剪二叉搜索树
- 解题思路:
- 递归法
- 迭代法:
- 题目二: 108.将有序数组转换为二叉搜索树
- 解题思路
- 递归法:
- 迭代法
- 题目三:538.把二叉搜索树转换为累加树
- 解题思路:
- 递归法
- 迭代法
- 二叉树总结篇
- 二叉树的理论基础
- 二叉树的遍历方式
- 求二叉树的属性
- 二叉树的改造与修改
- 求二叉搜索树的属性
- 二叉树公共祖先问题
- 二叉搜索树的修改与改造
- 总结
二叉树 Part06
二、题目
题目一:669.修剪二叉搜索树
[669. 修剪二叉搜索树](https://leetcode.cn/problems/minimum-absolute-difference-in-bst/)
解题思路:
错误的思路:
直接想法就是:递归处理,然后遇到 root->val < low || root->val > high 的时候直接return NULL,一波修改,干净利落。
可以写出以下代码:
class Solution {
public:TreeNode* trimBST(TreeNode* root, int low, int high) {if (root == nullptr || root->val < low || root->val > high) return nullptr;root->left = trimBST(root->left, low, high);root->right = trimBST(root->right, low, high);return root;}
};
note:
但是会忽略掉删除节点的右子树,可能会存在符合的节点,但是上面的代码直接删除了,所以是不可行的。下图就是示例图:
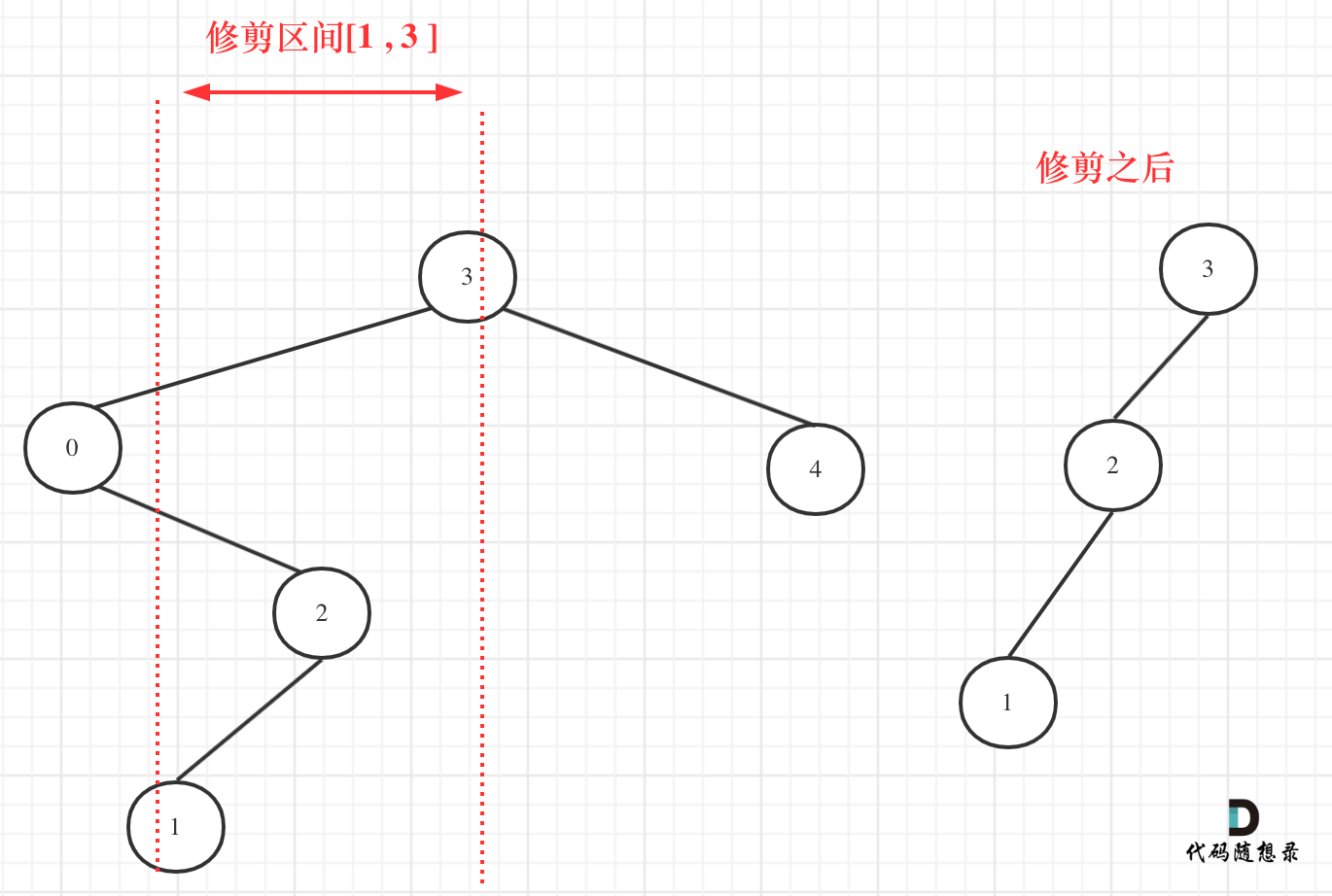
从图中可以看出需要重构二叉树,想想是不是本题就有点复杂了。
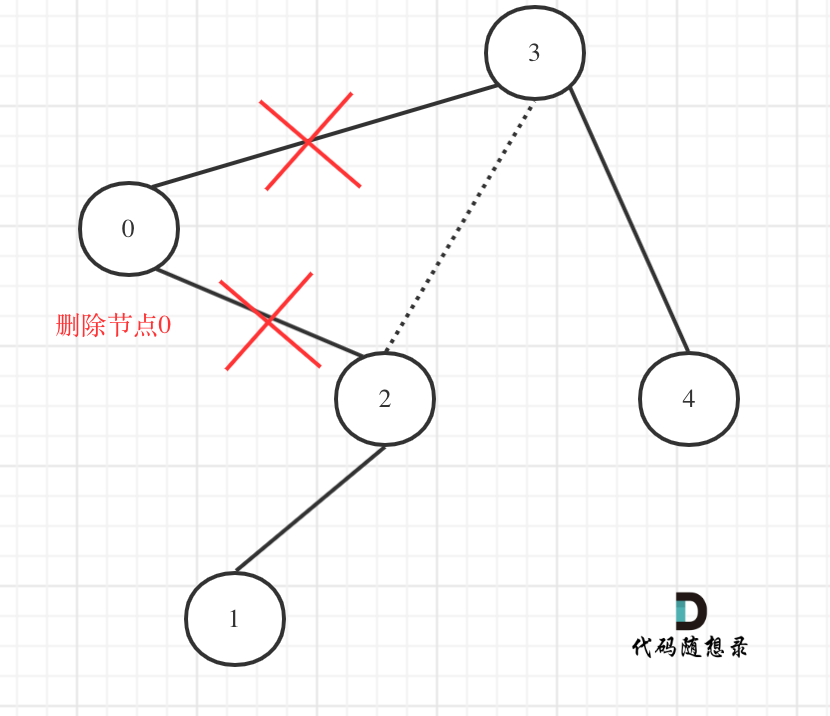
其实不用重构那么复杂。在上图中我们发现节点0并不符合区间要求,那么将节点0的右孩子 节点2 直接赋给 节点3的左孩子就可以了(就是把节点0从二叉树中移除),如图:
递归法
-
确定递归函数的参数以及返回值
这里我们为什么需要返回值呢?
因为是要遍历整棵树,做修改,其实不需要返回值也可以,我们也可以完成修剪(其实就是从二叉树中移除节点)的操作。
但是有返回值,更方便,可以通过递归函数的返回值来移除节点。
TreeNode* trimBST(TreeNode* root, int low, int high) -
确定终止条件
修剪的操作并不是在终止条件上进行的,所以就是遇到空节点返回就可以了。
if (root == nullptr ) return nullptr; -
确定单层递归的逻辑
如果root(当前节点)的元素小于low的数值,那么应该递归右子树,并返回右子树符合条件的头结点。
if (root->val < low) {TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点return right; }// 同理如果root(当前节点)的元素大于high的,那么应该递归左子树,并返回左子树符合条件的头结点。 if (root->val > high) {TreeNode* left = trimBST(root->left, low, high); // 寻找符合区间[low, high]的节点return left; }接下来要将下一层处理完左子树的结果赋给root->left,处理完右子树的结果赋给root->right。
最后返回root节点,代码如下:
这里可能是子树里面还有不符合要求的节点,所以还是要遍历一下的。
root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子 root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子 return root;Q:多余的节点究竟是如何从二叉树中移除的呢?
在回顾一下上面的代码,针对下图中二叉树的情况:
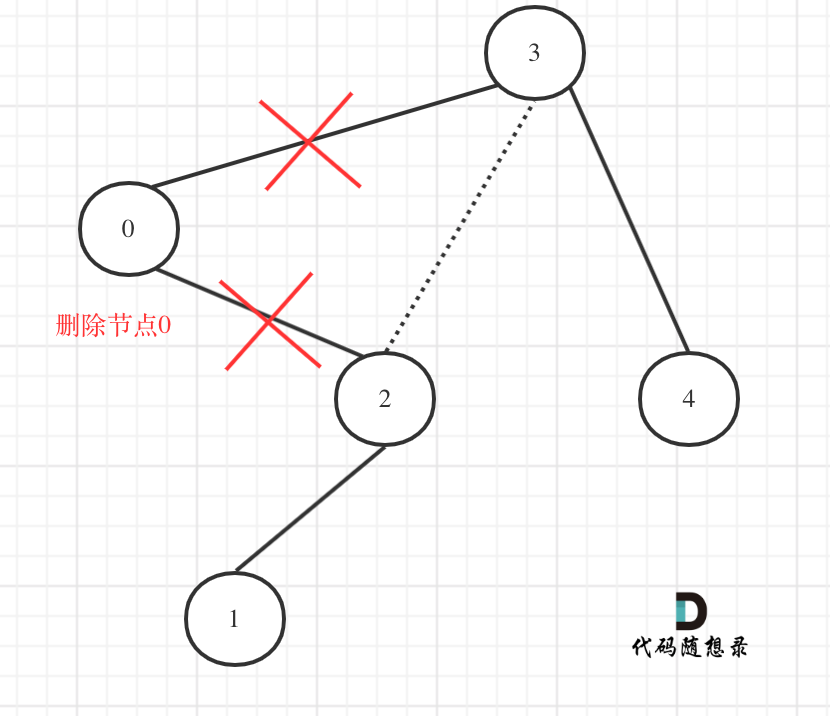
如下代码相当于把节点0的右孩子(节点2)返回给上一层,
if (root->val < low) {TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点return right; }然后如下代码相当于用节点3的左孩子 把下一层返回的 节点0的右孩子(节点2) 接住。
root->left = trimBST(root->left, low, high);此时节点3的左孩子就变成了节点2,将节点0从二叉树中移除了。
完整代码如下:
class Solution {
public:TreeNode* trimBST(TreeNode* root, int low, int high) {if (root == nullptr ) return nullptr;if (root->val < low) {TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点return right;}if (root->val > high) {TreeNode* left = trimBST(root->left, low, high); // 寻找符合区间[low, high]的节点return left;}root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子return root;}
};
精简之后:
class Solution {
public:TreeNode* trimBST(TreeNode* root, int low, int high) {if (root == nullptr) return nullptr;if (root->val < low) return trimBST(root->right, low, high);if (root->val > high) return trimBST(root->left, low, high);root->left = trimBST(root->left, low, high);root->right = trimBST(root->right, low, high);return root;}
};
迭代法:
因为二叉搜索树的有序性,不需要使用栈模拟递归的过程。
在剪枝的时候,可以分为三步:
- 将root移动到[L, R] 范围内,注意是左闭右闭区间
- 剪枝左子树
- 剪枝右子树
class Solution {
public:TreeNode* trimBST(TreeNode* root, int L, int R) {if (!root) return nullptr;// 处理头结点,让root移动到[L, R] 范围内,注意是左闭右闭while (root != nullptr && (root->val < L || root->val > R)) {if (root->val < L) root = root->right; // 小于L往右走else root = root->left; // 大于R往左走}TreeNode *cur = root;// 此时root已经在[L, R] 范围内,处理左孩子元素小于L的情况while (cur != nullptr) {while (cur->left && cur->left->val < L) {cur->left = cur->left->right;}cur = cur->left;}cur = root;// 此时root已经在[L, R] 范围内,处理右孩子大于R的情况while (cur != nullptr) {while (cur->right && cur->right->val > R) {cur->right = cur->right->left;}cur = cur->right;}return root;}
};
小结:
题目二: 108.将有序数组转换为二叉搜索树
108. 将有序数组转换为二叉搜索树
解题思路
- 本质就是寻找分割点,分割点作为当前节点,然后递归左区间和右区间。
- 因为有序数组构造二叉搜索树,寻找分割点就比较容易了。
- 分割点就是数组中间位置的节点。
Q:如果数组长度为偶数,中间节点有两个,取哪一个?
取哪一个都可以,只不过构成了不同的平衡二叉搜索树。
例如:输入:[-10,-3,0,5,9]
如下两棵树,都是这个数组的平衡二叉搜索树:
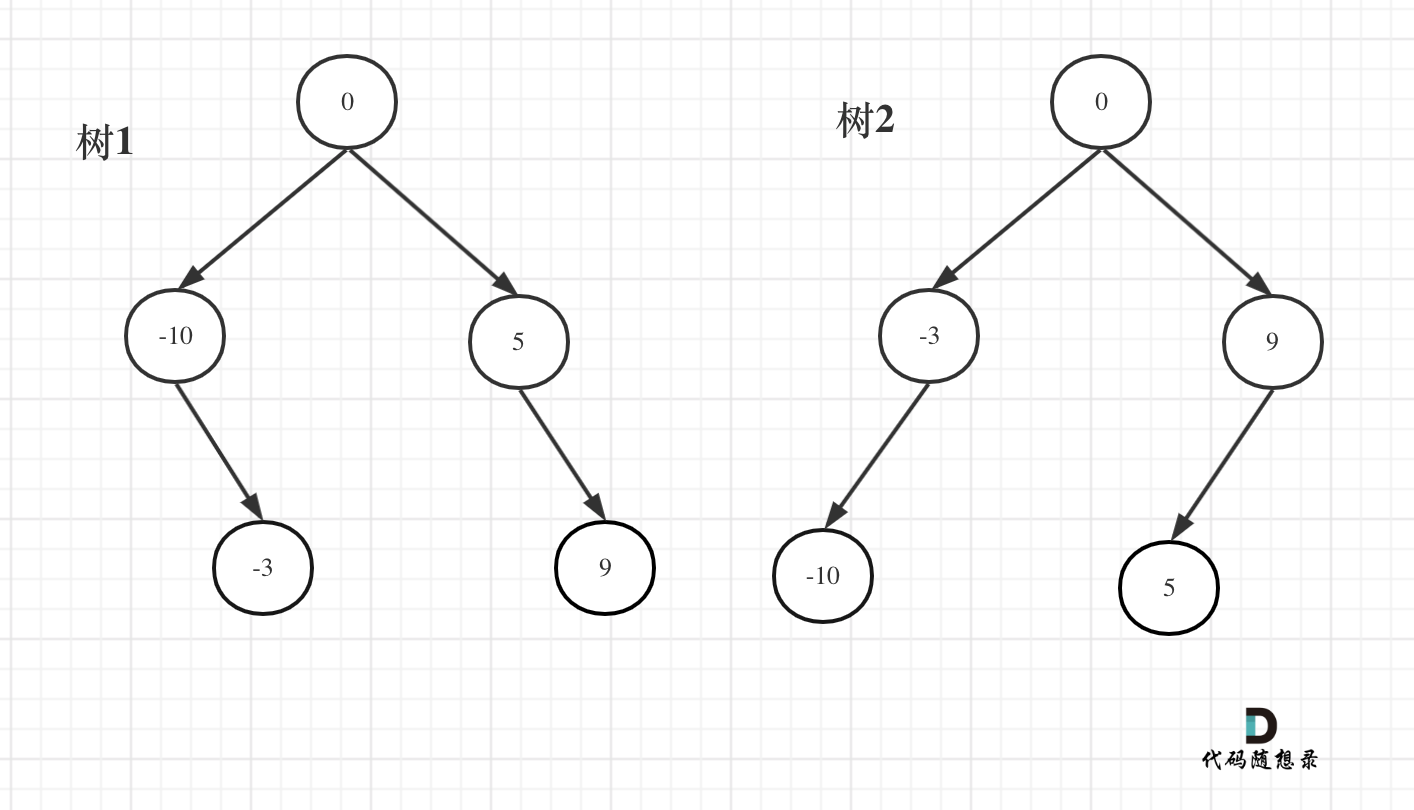
如果要分割的数组长度为偶数的时候,中间元素为两个,是取左边元素 就是树1,取右边元素就是树2。
这也是题目中强调答案不是唯一的原因。
递归法:
-
确定递归函数的返回值及参数
这里定义的是左闭右闭区间,在不断分割的过程中,也会坚持左闭右闭的区间,这又涉及之前讲过的循环不变量。
// 左闭右闭区间[left, right] TreeNode* traversal(vector<int>& nums, int left, int right) -
确定递归终止条件
这里定义的是左闭右闭的区间,所以当区间 left > right的时候,就是空节点了。
if (left > right) return nullptr; -
确定单层递归的逻辑
首先取数组中间元素的位置,不难写出int mid = (left + right) / 2;,这么写其实有一个问题,就是数值越界,例如left和right都是最大int,这么操作就越界了,在二分法中尤其需要注意!
**note:**所以可以这么写:int mid = left + ((right - left) / 2);
-
int mid = left + ((right - left) / 2); //首先取数组中间元素的位置 TreeNode* root = new TreeNode(nums[mid]); //取了中间位置,就开始以中间位置的元素构造节点 root->left = traversal(nums, left, mid - 1); //接着划分区间,root的左孩子接住下一层左区间的构造节点,右孩子接住下一层右区间构造的节点。 root->right = traversal(nums, mid + 1, right); return root;
这里int mid = left + ((right - left) / 2);的写法相当于是如果数组长度为偶数,中间位置有两个元素,取靠左边的。
整体C++代码如下:
class Solution {
private:TreeNode* traversal(vector<int>& nums, int left, int right) {if (left > right) return nullptr;int mid = left + ((right - left) / 2);TreeNode* root = new TreeNode(nums[mid]);root->left = traversal(nums, left, mid - 1);root->right = traversal(nums, mid + 1, right);return root;}
public:TreeNode* sortedArrayToBST(vector<int>& nums) {TreeNode* root = traversal(nums, 0, nums.size() - 1);return root;}
};
注意:在调用traversal的时候传入的left和right为什么是0和nums.size() - 1,因为定义的区间为左闭右闭。
迭代法
迭代法可以通过三个队列来模拟,一个队列放遍历的节点,一个队列放左区间下标,一个队列放右区间下标。
模拟的就是不断分割的过程,C++代码如下:
class Solution {
public:TreeNode* sortedArrayToBST(vector<int>& nums) {if (nums.size() == 0) return nullptr;TreeNode* root = new TreeNode(0); // 初始根节点queue<TreeNode*> nodeQue; // 放遍历的节点queue<int> leftQue; // 保存左区间下标queue<int> rightQue; // 保存右区间下标nodeQue.push(root); // 根节点入队列leftQue.push(0); // 0为左区间下标初始位置rightQue.push(nums.size() - 1); // nums.size() - 1为右区间下标初始位置while (!nodeQue.empty()) {TreeNode* curNode = nodeQue.front();nodeQue.pop();int left = leftQue.front(); leftQue.pop();int right = rightQue.front(); rightQue.pop();int mid = left + ((right - left) / 2);curNode->val = nums[mid]; // 将mid对应的元素给中间节点if (left <= mid - 1) { // 处理左区间curNode->left = new TreeNode(0);nodeQue.push(curNode->left);leftQue.push(left);rightQue.push(mid - 1);}if (right >= mid + 1) { // 处理右区间curNode->right = new TreeNode(0);nodeQue.push(curNode->right);leftQue.push(mid + 1);rightQue.push(right);}}return root;}
};
小结:
- 递归思路:提到了递归方法的核心思路是不断进行中间分割,然后递归地处理左区间和右区间,这也是一种分治策略。
- 递归函数的返回值:通过递归函数的返回值来增删二叉树是常规操作。
- 循环不变量的重要性:在定义区间的过程中,再次强调了循环不变量的重要性,这可能是在递归或迭代过程中保持逻辑一致性的关键。
- 迭代方法:这实际上是模拟取中间元素,然后不断分割去构造二叉树的过程。
- 递归与迭代的比较:虽然递归方法可能更直观,但迭代方法提供了另一种解决问题的途径,特别是在某些情况下可能更高效或更适合某些应用场景。
题目三:538.把二叉搜索树转换为累加树
538. 把二叉搜索树转换为累加树
解题思路:
- 当我们面对累加二叉搜索树的问题时,可能会感到困惑,因为直观上它看起来比操作数组要复杂。
- 使得每个节点
node的新值等于原树中大于或等于node.val的值之和。 - 但一旦我们认识到二叉搜索树的有序性,问题就变得简单了。就像处理一个有序数组[2, 5, 13],我们可以从后向前进行累加,得到新的数组[20, 18, 13]。
- 这种遍历方式在数组中很常见,而在二叉搜索树中,我们只需要调整遍历的顺序,采用反中序遍历(即先遍历右子树,然后是根节点,最后是左子树),就可以实现同样的顺序累加。这样一来,原本看似复杂的累加操作,就变成了一个简单的遍历和累加过程。
递归法
pre指针的使用技巧: 本题依然需要一个pre指针记录当前遍历节点cur的前一个节点,这样才方便做累加。
递归三部曲:
-
确定递归函数的返回值和参数
nt pre = 0; // 记录前一个节点的数值 void traversal(TreeNode* cur) -
确定递归函数的终止条件
if (cur == NULL) return; -
确定单层循环逻辑
注意要右中左来遍历二叉树, 中节点的处理逻辑就是让cur的数值加上前一个节点的数值。
traversal(cur->right); // 右 cur->val += pre; // 中 pre = cur->val; traversal(cur->left); // 左
完整代码如下:
class Solution {
private:int pre = 0; // 记录前一个节点的数值void traversal(TreeNode* cur) { // 右中左遍历if (cur == NULL) return;traversal(cur->right);cur->val += pre;pre = cur->val;traversal(cur->left);}
public:TreeNode* convertBST(TreeNode* root) {pre = 0;traversal(root);return root;}
};
迭代法
迭代法其实就是中序模板题了,确定一个自己习惯的写法。
class Solution {
private:int pre; // 记录前一个节点的数值void traversal(TreeNode* root) {stack<TreeNode*> st;TreeNode* cur = root;while (cur != NULL || !st.empty()) {if (cur != NULL) {st.push(cur);cur = cur->right; // 右} else {cur = st.top(); // 中st.pop();cur->val += pre;pre = cur->val;cur = cur->left; // 左}}}
public:TreeNode* convertBST(TreeNode* root) {pre = 0;traversal(root);return root;}
};
二叉树总结篇
二叉树的理论基础
二叉树的种类、存储方式、遍历方式、定义方式
二叉树的遍历方式
- 深度优先遍历
- 广度优先遍历
求二叉树的属性
二叉树的改造与修改
求二叉搜索树的属性
二叉树公共祖先问题
二叉搜索树的修改与改造
小结:
note:二叉树的遍历顺序的选择
- 如果是要构造二叉树,无论是普通的二叉树还是二叉搜索树,通常都是先处理根节点,也就是前序遍历。
- 当我们想要计算普通二叉树的一些属性时,后序遍历是个不错的选择,因为这样可以在访问节点之前先得到其左右子树的信息,通常需要通过递归函数的返回值来进行计算。
- 而对于二叉搜索树,由于其元素是有序的,中序遍历是最佳选择,因为这样可以直接利用树的有序性,比如进行排序或查找操作。
注意在普通二叉树的属性中,用的是一般为后序,例如单纯求深度就用前序,二叉树:找所有路径 (opens new window)也用了前序,这是为了方便让父节点指向子节点。
所以求普通二叉树的属性还是要具体问题具体分析,才能让问题变得简洁。
总结
学到了那些东西:
- 二叉树的构造(前序构造),二叉树的遍历方式(前中后)
- 递归和迭代,一般递归的思路来的比较简单,代码也是比较简洁。递归三部曲(1.2.3)。
- pre指针的使用,这是一个技巧。
- 看到二叉搜索树,一定要记得利用他的特性,有序。(在本节,迭代的代码也是比较简单的。)
关于二叉树的章节,今天是完结篇,整体下来,学的有些稀里糊涂,大概过了一边,顺了一遍思路。很多题目自己为了节省时间,还有偷懒,就没有自己亲手去敲的,不知道是因为自己太懒还是太烂,总有畏难情绪,觉得自己敲了也敲不对,敲了也没用只是浪费时间,就有些投机取巧,没有去敲。这样下来,总感觉收获很少,但哪位老板能和我说一下,你们是怎么坚持,每题都敲代码的吗?(这对我很重要)
总之,二叉树,这一个章节也是结束了,马上要开始一个新的章节回溯,杜绝懒惰,从我做起,加油!!
相关文章:

Day 21代码|随想录| 二叉树完结撒花,今日刷题669.修剪二叉搜索树、108.将有序数组转换为二叉搜索树、538.吧二叉搜索树转换为累加树
提示:DDU,供自己复习使用。欢迎大家前来讨论~ 文章目录 二叉树 Part06二、题目题目一:669.修剪二叉搜索树解题思路:递归法迭代法: 题目二: 108.将有序数组转换为二叉搜索树解题思路递归法:迭代…...

cmake教程一
1. Start 1.1 构建简单工程 cmake_minimum_required(VERSION 3.0) project(Step1) add_executable(Step1 main.cpp)设置cmake最低版本要求设置工程名字设置工程生成可执行程序 2. 声明 C Standard set(CMAKE_CXX_STANDARD 11) set(CMAKE_CXX_STANDARD_REQUIRED True)如果我…...

3D场景标注标签信息,three.js CSS 2D渲染器CSS2DRenderer、CSS 3D渲染器CSS3DRenderer(结合react)
如果你想用HTML元素作为标签标注三维场景中模型信息,需要考虑定位的问题。比如一个模型,在代码中你可以知道它的局部坐标或世界坐标xyz,但是你并不知道渲染后在canvas画布上位置,距离web页面顶部top和左侧的像素px值。自己写代码把…...

C++参悟-单例模式
单例模式 一、概述1. 特点2. 实现方式3. 应用场景 二、实现代码1. 静态局部变量的懒汉单例2. 加锁的懒汉式单例3. 使用 C11 中的 std::call_one 的懒汉单例4. 饿汉式单例 一、概述 这里记录一下单例模式的最常用使用,单例模式(Single Pattern࿰…...

【题解】—— LeetCode一周小结32
🌟欢迎来到 我的博客 —— 探索技术的无限可能! 🌟博客的简介(文章目录) 【题解】—— 每日一道题目栏 上接:【题解】—— LeetCode一周小结31 5.不含连续1的非负整数 题目链接:600. 不含连续…...
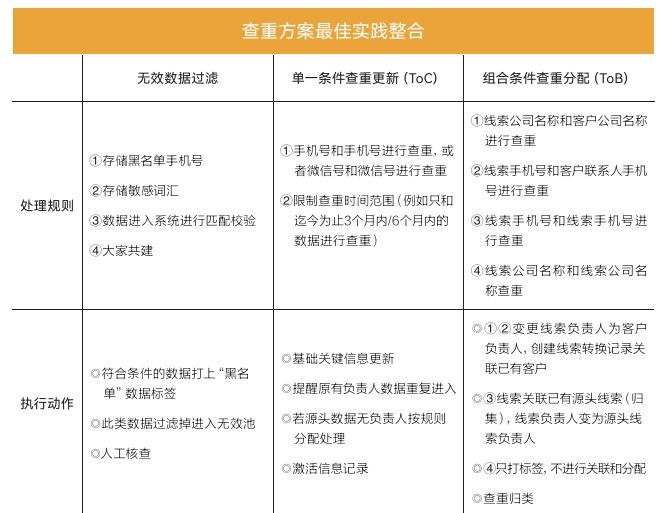
详解线索分层的目的、维度与创新实践
线索分层是一个系统性的过程,旨在更有效地管理、跟踪和利用线索资源。这一过程可以借鉴多种策略和方法,特别是在用户运营和市场营销中。 1、线索分层的目的 线索分层的主要目的是根据线索的不同特征或成熟度,将其分类管理,以便更…...

于8月21号的回顾
傍晚的日落和逐渐深邃的夜,驱散了白天的极致闷热。倦怠和疲惫充斥着大脑,喧嚣的浮沉又在耳边轰鸣。 我不曾想到,再次打开博客已经是两年后的今天了。手指轻轻滑过鼠标,博客的页面缓缓加载,那些被时间尘封的记忆瞬间涌…...

Abstract Class抽象类
抽象类(Abstract Class)在面向对象编程中是一种特殊的类,它不能被实例化,即不能创建该类的对象。抽象类主要用于定义一组接口(即方法),这些方法的具体实现由子类来完成。抽象类通常用于表示一种…...

webrtc ns 降噪之粉红噪声参数推导
webrtc中降噪中,前50帧需要进行简单噪声估计,使用白噪声和粉红噪声模型估算。 首先我们 复习 有色噪声(包含白噪声)的一般模型: S(f) 是频率 f 处的功率谱密度。f是频率。α 是一个频谱指数,通常在1左右。…...

IO进程线程8月21日
1,思维导图 2,登录 #ifndef __LOG_H__ #define __LOG_H__ #include<myhead.h> typedef struct {char name[20];char pwd[20]; }str;int regist();int login(); #endif#include"log.h" int login() {char a[20]"\n";str p,s;…...

Web安全:SqlMap工具
一、简介 sqlmap 是一款开源的渗透测试工具,可以自动化进行SQL注入的检测、利用,并能接管数据库服务器。它具有功能强大的检测引擎,为渗透测试人员提供了许多专业的功能并且可以进行组合,其中包括数据库指纹识别、数据读取和访问底层文件系统…...
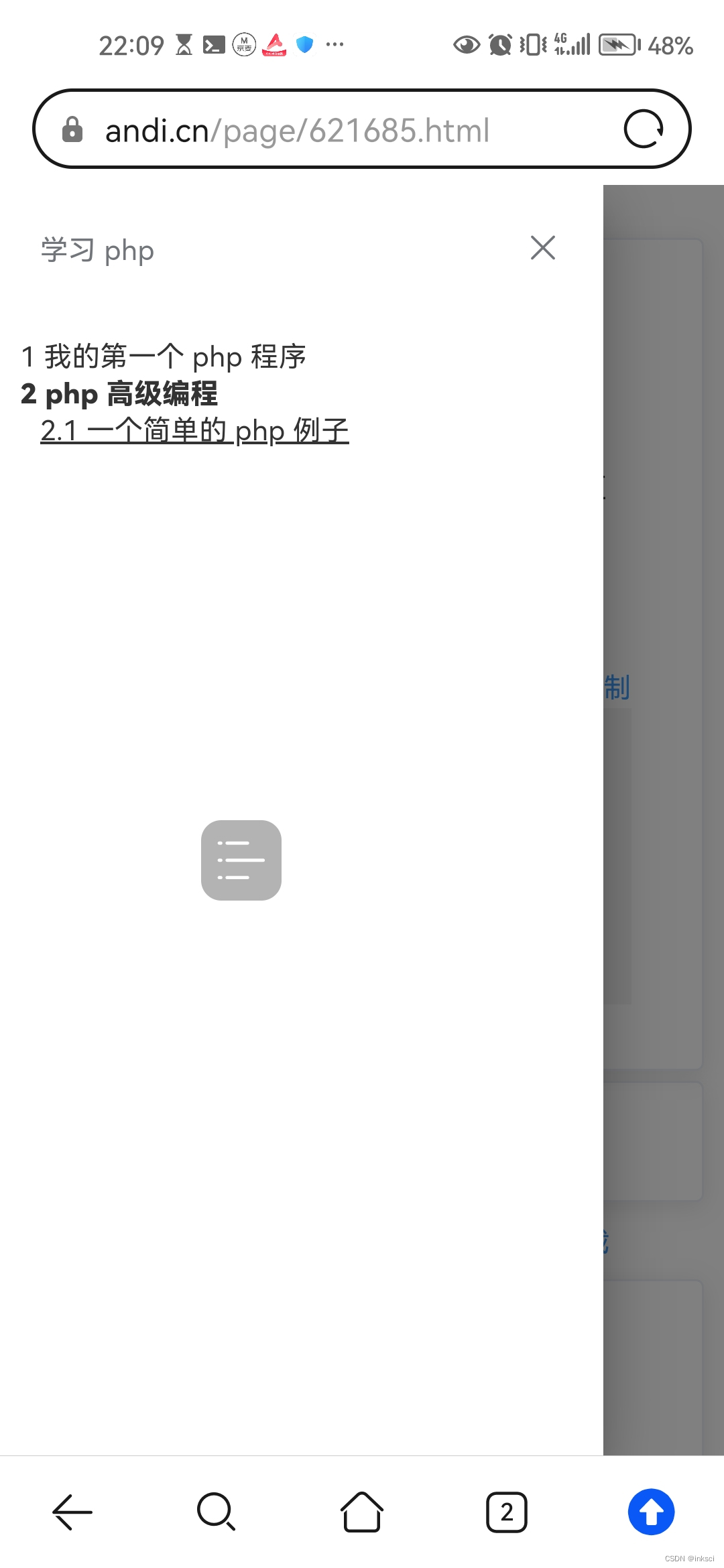
用手机写一本电子书
第1步、进入Andi.cn网站 第2步、点击登录,注册用户 第3步、点击去创作,进入创作页面 第4步、点击右下角的小笔,写一篇文章 第5步、下翻,点击提交按钮 第6步、再写一篇文章 第7步、点击栏目设计 第8步、进入栏目设计,点…...

【网络编程】基于UDP的TFTP文件传输
1)tftp协议概述 简单文件传输协议,适用于在网络上进行文件传输的一套标准协议,使用UDP传输 特点: 是应用层协议 基于UDP协议实现 数据传输模式 octet:二进制模式(常用) mail:已经不再…...

Vue 3 + Pinia 实现网页刷新功能
概述 在现代 Web 开发中,保持用户界面的动态性和响应性至关重要。当用户触发某些操作时,例如点击按钮或者完成表单提交,我们往往需要刷新页面的一部分来展示最新的数据。本文将介绍如何使用 Vue 3 和 Pinia 来实现这一功能。 技术栈 Vue 3…...
DVWA综合靶场漏洞讲解
目录 综合靶场漏洞讲解 Brute Force Low Medium High Command Injection Low Medium High File Inclusion Low,Medium,High File Upload Low Medium High SQL Injection Low Medium High SQL Injection (Blind) Low Medium High XSS(DOM&am…...

实现Bezier样条曲线
1.给出n1 个控制点pk(xk,yk,zk),这里k可取值0-n,多项式函数公式如下 获取的单个点的代码 void zmBezier::getPoint(float u, double p[3]) {int n m_count - 1;double x 0, y 0, z 0;for(int k 0; k < n; k){x m_ctrlPoints[k][0] * BEZ_k_n(n, k, u);y m_ctrlPoin…...

MySQL中的EXPLAIN的详解
一、介绍 官网介绍: https://dev.mysql.com/doc/refman/5.7/en/explain-output.htmlhttps://dev.mysql.com/doc/refman/8.0/en/explain-output.htmlexplain(执行计划),使用explain关键字可以模拟优化器执行sql查询语句ÿ…...

LearnOpenGL——SSAO学习笔记
LearnOpenGL——SSAO学习笔记 SSAO一、基本概念二、样本缓冲三、法向半球四、随机核心转动五、SSAO着色器六、环境遮蔽模糊七、应用SSAO遮蔽因子 SSAO 一、基本概念 环境光照是我们加入场景总体光照中的一个固定光照常量,它被用来模拟光的散射(Scattering)。散射应…...

[C语言]-基础知识点梳理-文件管理
前言 各位师傅们好,我是qmx_07,今天给大家讲解文件管理的相关知识,也就是常见的 读取,删除一类的操作 文件 为什么要使用文件? 程序的数据是存储在电脑的内存中,如果程序退出,内存回收&…...
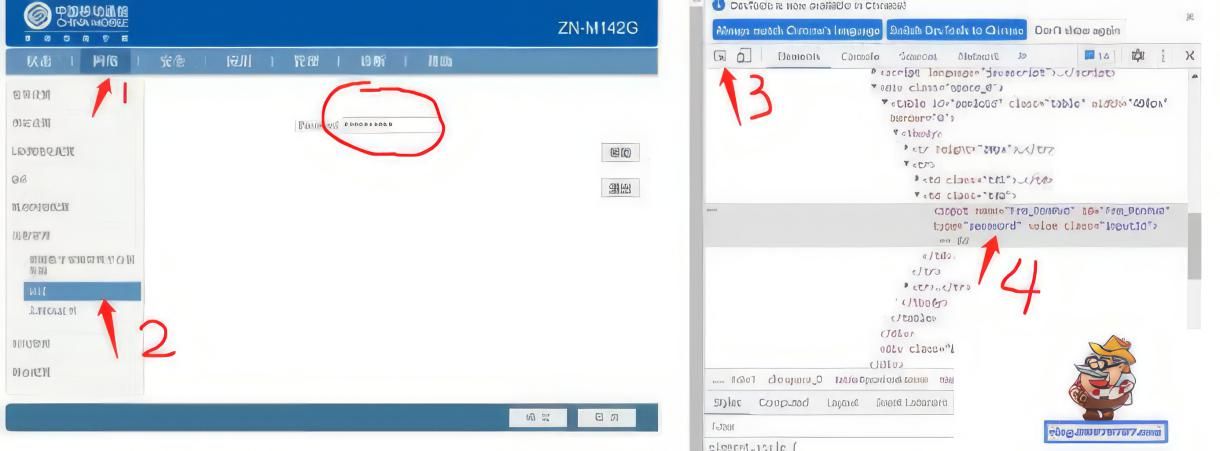
pcdn闲置带宽被动收入必看教程。第五讲:光猫更换和基础设置
PCDN闲置带宽被动收入必看教程 —— 第五讲:光猫更换和基础设置 为了从闲置带宽中获得被动收入,高效的网络设备至关重要。运营商提供的光猫通常能满足日常家用需求,但对于PCDN应用来说,它们可能不足以提供所需的高性能和稳定性。…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
