EmguCV学习笔记 C# 2.2 Matrix类
版权声明:本文为博主原创文章,转载请在显著位置标明本文出处以及作者网名,未经作者允许不得用于商业目的。
EmguCV学习笔记目录 Vb.net
EmguCV学习笔记目录 C#
笔者的博客网址:VB.Net-CSDN博客
教程相关说明以及如何获得pdf教程和代码(博客上的教程内容会和pdf教程一致,教程中也会包含所有代码),请移步:EmguCV学习笔记
2.2 Matrix类
Matrix类是EmguCV中的一个矩阵类,它可以用来存储和处理矩阵数据,可以处理任意维度的矩阵。与Mat类相比,Matrix类提供了更多的矩阵运算方法,如矩阵加减、乘法、逆矩阵等,也更加灵活,而且底层实现也更加高效。
通常而言,Matrix类应为Matrix<数据类型> 的形式,其中数据类型指明了该矩阵中元素的存储类型,包括byte、int、float等。
2.2.1 构造函数
为了显示Matrix的结果,请在窗体上放置一个MatrixBox控件。该控件位于【工具箱】|【Emgu.CV】下面。另外,
1、使用一维数组初始化Matrix:
【代码位置:frmChapter2_1】Button1_Click
//Matrix构造函数:一维数组初始化Matrix
private void Button1_Click(object sender, EventArgs e)
{
byte[] inputBytes = new Byte[] { 1, 2, 3, 4, 5, 6, 7, 8, 9 };
Matrix<byte> matr = new Matrix<byte>(inputBytes);
MatrixBox1.Matrix = matr;
}
显示结果如下:

图2-2 一维数组初始化Matrix
2、使用二维数组初始化Matrix:
【代码位置:frmChapter2_1】Button2_Click
//Matrix构造函数:二维数组初始化Matrix
private void Button2_Click(object sender, EventArgs e)
{
byte[,] inputBytes = new byte[,] { { 1, 2, 3 }, { 3, 4, 5 }, { 5, 6, 7 }, { 7, 8, 9 } };
Matrix<byte> matr = new Matrix<byte>(inputBytes);
MatrixBox1.Matrix = matr;
}
显示结果如下:

图2-3 二维数组初始化Matrix
3、指定大小初始化Matrix,然后写入值:
【代码位置:frmChapter2_1】Button3_Click
//Matrix构造函数:初始化矩阵的大小(Size)
//注意使用size的话,width是列,height是行,列在前,行灾后
//以下创建的是一个2列4行的矩阵
private void Button3_Click(object sender, EventArgs e)
{
byte[] inputBytes = new Byte[] { 1, 2, 3, 4, 5, 6, 7, 8 };
Matrix<byte> matr = new Matrix<byte>(new Size(2, 4));
for (int i = 0; i <= 1; i++)
for (int j = 0; j <= 3; j++)
matr[j, i] = inputBytes[i * 4 + j];
MatrixBox1.Matrix = matr;
}
先是初始化一个2列(Width)4行(Height)的矩阵,然后使用循环,将数组的数据写入矩阵。
显示结果如下:

图2-4 指定大小初始化Matrix
也可以通过SetValue方法设置相同的值:
【代码位置:frmChapter2_1】Button4_Click
//Matrix构造函数:初始化矩阵的大小(Size)
private void Button4_Click(object sender, EventArgs e)
{
Matrix<byte> matr = new Matrix<byte>(new Size(2, 4));
//将所有元素 设置相同的指定值
matr.SetValue(new MCvScalar(20));
MatrixBox1.Matrix = matr;
}
显示结果如下:

图2-5 对Matrix的元素设置相同的值
4、指定行、列、通道初始化Matrix,并将向每个通道写入相同的值:
【代码位置:frmChapter2_1】Button5_Click
//Matrix构造函数:行、列、通道初始化矩阵
private void Button5_Click(object sender, EventArgs e)
{
//row是行,col是列,行在前,列在后
//以下创建的是一个2列4行3通道的矩阵
Matrix<byte> matr = new Matrix<byte>(4, 3, 3);
//设置各个通道的元素的值
matr.SetValue(new MCvScalar(20, 30, 40));
MatrixBox1.Matrix = matr;
}
显示结果如下:

图2-6 对多通道Matrix的元素设置相同的值
注意:这个构造函数和通过Size方式初始化Matrix的构造函数有所区别的是,行和列出现的先后不同。Size(列,行),而这个是行、列、通道。
这里对Matrix元素的每个通道设置了值,在MatrixBox控件中可以在channel处下拉选择查看不同通道的值。
5、指定行、列、通道初始化Matrix,并将每个通道的值设置为0:
【代码位置:frmChapter2_1】Button6_Click
//Matrix元素的值全部设置为0(多通道设置每个通道为0)
private void Button6_Click(object sender, EventArgs e)
{
Matrix<byte> matr = new Matrix<byte>(4, 3, 3);
matr.SetZero();
MatrixBox1.Matrix = matr;
}
显示结果如下:

图2-7 设置多通道Matrix的元素的值为0
2.2.2 获取Matrix元素的值
在以下代码中提供了3种方法来获取Matrix指定位置(行,列)的值。
【代码位置:frmChapter2_1】Button7_Click
private void Button7_Click(object sender, EventArgs e)
{
byte[,] inputBytes = new byte[,] { { 1, 2, 3 }, { 3, 4, 5 }, { 5, 6, 7 }, { 7, 8, 9 } };
Matrix<byte> matr = new Matrix<byte>(inputBytes);
MatrixBox1.Matrix = matr;
//方法1:直接使用Matrix(行,列)进行输出,使用时需要注意行列的顺序
for(int i= 0;i< matr.Rows;i++)
{
for (int j = 0; j < matr.Cols; j++)
//通过matr[i,j]获得值的方式只适用于单通道矩阵
TextBox1.Text += matr[i, j] + " ";
TextBox1.Text += "\r\n";
}
TextBox1.Text += "====================" + "\r\n";
//方法2:先读取到一维数组,再输出
byte[] outputBytes1;
outputBytes1 = matr.Bytes;
int height = matr.Rows;
int width = matr.Cols;
for (int i = 0; i < height; i++)
{
for (int j = 0; j < width; j++)
TextBox1.Text += outputBytes1[i * width + j] + " ";
TextBox1.Text += "\r\n";
}
TextBox1.Text += "====================" + "\r\n";
//方法3:先读取到二维数组,再输出
byte[,] outputBytes2;
outputBytes2 = matr.Data;
//这里是二维数组,所以返回2
int outputBytesRank = outputBytes2.Rank;
for (int i = 0; i < outputBytes2.GetLength(0); i++)
{
for (int j = 0; j < outputBytes2.GetLength(1); j++)
TextBox1.Text += outputBytes2[i, j] + " ";
TextBox1.Text += "\r\n";
}
}
注意:只适合单通道Matrix。对于多通道Matrix需要将其分解成多个单通道Matrix再进行处理。
显示结果如下:

图2-8 读取单通道矩阵元素的值
2.2.3 Matrix的拆分
使用Matrix的Split方法将多通道矩阵拆分为单通道矩阵。
【代码位置:frmChapter2_1】Button8_Click
//将多通道Matrix拆分为多个单通道Matrix
private void Button8_Click(object sender, EventArgs e)
{
Matrix<byte> matr = new Matrix<byte>(4, 2, 3);
matr.SetValue(new MCvScalar(20, 30, 40));
Matrix<byte>[] arrMatr;
//使用Split方法拆分多通道矩阵到矩阵数组。
arrMatr = matr.Split();
//显示第一个通道的值
MatrixBox1.Matrix = arrMatr[0];
}
显示结果如下:

图2-9 Matrix第一个通道的值
2.2.4 Matrix的运算
2.2.4.1 加法
1、加一个数值
【代码位置:frmChapter2_1】Button9_Click
//Matrix的加法1:增加一个固定值
private void Button9_Click(object sender, EventArgs e)
{
byte[,] inputBytes = new byte[,] { { 1, 2, 3 }, { 3, 4, 5 }, { 5, 6, 7 }, { 7, 8, 9 } };
Matrix<byte> matr1 = new Matrix<byte>(inputBytes);
Matrix<byte> matr2;
//方法1:
matr2 = matr1 + 30;
//方法2:
//matr2 = matr1.Add(30);
MatrixBox1.Matrix = matr2;
}
显示结果如下:

图2-10 Matrix增加一个固定值
2、两个单通道矩阵相加
【代码位置:frmChapter2_1】Button10_Click
//Matrix的加法2:两个单通道矩阵相加
private void Button10_Click(object sender, EventArgs e)
{
byte[,] inputBytes1 = new byte[,] { { 1, 2, 3 }, { 3, 4, 5 }, { 5, 6, 7 }, { 7, 8, 9 } };
byte[,] inputBytes2 = new byte[,] { { 3, 4, 5 }, { 5, 6, 7 }, { 7, 8, 9 }, { 9, 10, 11 } };
Matrix<byte> matr1=new Matrix<byte>(inputBytes1);
Matrix<byte> matr2 = new Matrix<byte>(inputBytes2);
Matrix<byte> matr3 = new Matrix<byte>(4, 3, 1);
//方法1:
matr3 = matr1 + matr2;
//方法2:
//matr3 = matr1.Add(matr2);
//方法3:
//CvInvoke.Add(matr1, matr2, matr3);
MatrixBox1.Matrix = matr3;
}
显示结果如下:

图2-11 两个单通道矩阵相加
注意:如果使用方法3,那么必须初始化matr3,否则可以不用初始化,即:
Matrix<byte> matr3;
下同。
3、两个多通道矩阵相加
【代码位置:frmChapter2_1】Button11_Click
//Matrix的加法3:两个多通道矩阵相加
private void Button11_Click(object sender, EventArgs e)
{
Matrix<byte> matr1 = new Matrix<byte>(4, 3, 3);
matr1.SetValue(new MCvScalar(20, 30, 40));
Matrix<byte> matr2 = new Matrix<byte>(4, 3, 3);
matr2.SetValue(new MCvScalar(50, 20, 240));
Matrix<byte> matr3 = new Matrix<byte>(4, 3, 3);
//方法1:
matr3 = matr1 + matr2;
//方法2:
///matr3 = matr1.Add(matr2);
//方法3:
//CvInvoke.Add(matr1, matr2, matr3);
MatrixBox1.Matrix = matr3;
}
显示结果如下:

图2-12 两个多通道矩阵相加
2.2.4.2 减法
1、减一个数值
【代码位置:frmChapter2_1】Button12_Click
//Matrix的减法1:减去一个固定值
private void Button12_Click(object sender, EventArgs e)
{
byte[,] inputBytes= new byte[,] { { 1, 2, 3 }, { 3, 4, 5 }, { 5, 6, 7 }, { 7, 8, 9 } };
Matrix<byte> matr1 = new Matrix<byte>(inputBytes);
Matrix<byte> matr2;
//方法1:
matr2 = matr1-3;
//方法2:
//matr2 = matr1.Sub(3);
MatrixBox1.Matrix = matr2;
}
显示结果如下:

图2-13 Matrix减去一个固定值
还有一个反向减法的方法,读者可以测试将以上代码中的
matr2 = matr1.Sub(3);
替换为:
matr2 = matr1.SubR(30);
进行测试。
2、两个单通道矩阵相减
【代码位置:frmChapter2_1】Button13_Click
//Matrix的减法2:两个单通道矩阵相减
private void Button13_Click(object sender, EventArgs e)
{
byte[,] inputBytes1 = new byte[,] { { 1, 2, 3 }, { 3, 4, 5 }, { 5, 6, 7 }, { 7, 8, 9 } };
byte[,] inputBytes2 = new byte[,] { { 3, 4, 5 }, { 5, 6, 7 }, { 7, 8, 9 }, { 9, 10, 21 } };
Matrix<byte> matr1 = new Matrix<byte>(inputBytes1);
Matrix<byte> matr2 = new Matrix<byte>(inputBytes2);
Matrix<byte> matr3 = new Matrix<byte>(4, 3, 1);
//方法1:
matr3 = matr2 - matr1;
//方法2:
//matr3 = matr2.Sub(matr1);
//方法3:
//CvInvoke.Subtract(matr2, matr1, matr3);
MatrixBox1.Matrix = matr3;
}
显示结果如下:

图2-14 两个单通道矩阵相减
3、两个多通道矩阵相减
【代码位置:frmChapter2_1】Button14_Click
//Matrix的减法3:两个多通道矩阵相减
private void Button14_Click(object sender, EventArgs e)
{
Matrix<byte> matr1 = new Matrix<byte>(4, 3, 3);
matr1.SetValue(new MCvScalar(20, 30, 40));
Matrix<byte> matr2 = new Matrix<byte>(4, 3, 3);
matr2.SetValue(new MCvScalar(50, 20, 240));
Matrix<byte> matr3 = new Matrix<byte>(4, 3, 3);
//方法1:
matr3 = matr2 - matr1;
//方法2:
//matr3 = matr2.Sub(matr1);
//方法3:
//CvInvoke.Subtract(matr2, matr1, matr3);
MatrixBox1.Matrix = matr3;
}
显示结果如下:

图2-15 两个多通道矩阵相减
2.2.4.3 乘法
1、乘以一个数值
【代码位置:frmChapter2_1】Button15_Click
//Matrix的乘法1:乘以一个固定值
private void Button15_Click(object sender, EventArgs e)
{
byte[,] inputBytes = new byte[,] { { 1, 2, 3 }, { 3, 4, 5 }, { 5, 6, 7 }, { 7, 8, 9 } };
Matrix<byte> matr1 = new Matrix<byte>(inputBytes);
Matrix<byte> matr2 ;
//方法1:
matr2 = matr1 * 3;
//方法2:
//matr2 = matr1.Mul(3);
MatrixBox1.Matrix = matr2;
}
显示结果如下:

图2-16 Matrix乘以一个数值
2、两个单通道矩阵相乘
注意:两个矩阵相乘必须满足一定条件
1、第一个Matrix的列数应等于第二个Matrix的行数,生成结果为
列数=第二个Matrix的列数
行数=第一个Matrix的行数
2、数据类型要一致,整数型数据(包括byte、int、Long、Int16、Int32、Int64等)不能进行乘法运算,浮点型数据(Single、float、Double)可以参与运算。
【代码位置:frmChapter2_1】Button16_Click
//Matrix的乘法2:两个单通道矩阵相乘
private void Button16_Click(object sender, EventArgs e)
{
//4列2行
Single[,] inputBytes1 = new Single[,] { { 1, 2, 3, 4 }, { 3, 4, 5, 6 } };
//3列4行
Single[,] inputBytes2 = new Single[,]{ { 1, 2, 3 }, { 3, 4, 5 }, { 5, 6, 7 }, { 7, 8, 9 } };
Matrix<Single> matr1 = new Matrix<Single>(inputBytes1);
Matrix<Single> matr2 = new Matrix<Single>(inputBytes2);
//生成3列2行
Matrix<Single> matr3;
//方法1:
matr3 = matr1 * matr2;
//方法2:
//matr3 = matr1.Mul(matr2);
MatrixBox1.Matrix = matr3;
}
显示结果如下:

图2-17 两个单通道矩阵相乘
3、两个多通道矩阵相乘
两个多通道矩阵似乎不能直接相乘
4、两个矩阵对应元素相乘
这个方法将两个矩阵对应坐标位置的元素相乘,有别于标准的矩阵乘法。
【代码位置:frmChapter2_1】Button17_Click
//Matrix的乘法3:行列对应元素相乘,不同于普通的矩阵乘法
private void Button17_Click(object sender, EventArgs e)
{
byte[,] inputBytes1 = new byte[,] { { 1, 2, 3 }, { 3, 4, 5 }, { 5, 6, 7 }, { 7, 8, 9 } };
byte[,] inputBytes2 = new byte[,] { { 3, 4, 5 }, { 5, 6, 7 }, { 7, 8, 9 }, { 9, 10, 11 } };
Matrix<byte> matr1 = new Matrix<byte>(inputBytes1);
Matrix<byte> matr2 = new Matrix<byte>(inputBytes2);
matr1._Mul(matr2);
MatrixBox1.Matrix = matr1;
}
显示结果如下:

图2-18 两矩阵对应元素相乘
2.2.4.4 除法
【代码位置:frmChapter2_1】Button18_Click
//Matrix的除法
private void Button18_Click(object sender, EventArgs e)
{
Single[,] inputBytes = new Single[,] { { 1, 2, 3 }, { 3, 4, 5 }, { 5, 6, 7 }, { 7, 8, 9 } };
Matrix<Single> matr1 = new Matrix<Single>(inputBytes);
Matrix<Single> matr2;
matr2 = matr1 / 3;
MatrixBox1.Matrix = matr2;
}
显示结果如下:

图2-19 Matrix除以一个数值
2.2.4.5 Not运算
【代码位置:frmChapter2_1】Button19_Click
//矩阵的Not
private void Button19_Click(object sender, EventArgs e)
{
byte[,] inputBytes1 = new byte[,] { { 1, 2, 3 }, { 3, 4, 5 }, { 5, 6, 7 }, { 7, 8, 9 } };
Matrix<byte> matr1 = new Matrix<byte>(inputBytes1);
matr1._Not();
MatrixBox1.Matrix = matr1;
}
显示结果如下:

图2-20 Matrix的Not运算
读者可自行对比byte数据类型和short、int等类型生成的结果。
2.2.5 Matrix拼接
Matrix提供了ConcateHorizontal、ConcateVertical方法将两个矩阵拼接为一个矩阵。
- ConcateHorizontal:水平方向拼接,必须具备相同行数。
- ConcateVertical:垂直方向拼接,必须具备相同列数
【代码位置:frmChapter2_1】Button20_Click
//矩阵的水平方向拼接,必须具备相同行数
private void Button20_Click(object sender, EventArgs e)
{
byte[,] inputBytes1 = new byte[,] { { 1, 2, 3 }, { 3, 4, 5 }, { 5, 6, 7 }, { 7, 8, 9 } };
byte[,] inputBytes2 = new byte[,] { { 3, 4 }, { 5, 6 }, { 7, 8 }, { 9, 10 } };
Matrix<byte> matr1 = new Matrix<byte>(inputBytes1);
Matrix<byte> matr2 = new Matrix<byte>(inputBytes2);
Matrix<byte> matr3;
matr3 = matr1.ConcateHorizontal(matr2);
MatrixBox1.Matrix = matr3;
}
显示结果如下:

图2-21 Matrix水平方向拼接
【代码位置:frmChapter2_1】Button21_Click
//矩阵的垂直方向拼接,必须具备相同列数
private void Button21_Click(object sender, EventArgs e)
{
byte[,] inputBytes1 = new byte[,] { { 1, 2, 3 }, { 3, 4, 5 }, { 5, 6, 7 }, { 7, 8, 9 } };
byte[,] inputBytes2 = new byte[,] { { 3, 4, 5 }, { 5, 6, 7 }, { 7, 8, 9 } };
Matrix<byte> matr1 = new Matrix<byte>(inputBytes1);
Matrix<byte> matr2 = new Matrix<byte>(inputBytes2);
Matrix<byte> matr3;
matr3 = matr1.ConcateVertical(matr2);
MatrixBox1.Matrix = matr3;
}
显示结果如下:

图2-22 Matrix垂直方向拼接
2.2.6 随机矩阵
Matrix类提供了SetRandNormal方法来生成指定大小、类型和均值方差的随机矩阵。该方法声明如下:
public void SetRandNormal(MCvScalar mean, MCvScalar std)
其中参数:
- mean:均值,表示随机矩阵的平均值。在正态分布中,均值是分布的中心位置。均值越大,生成的随机矩阵的像素值越偏向于均值。
- std:标准差,表示随机矩阵的离散程度。在正态分布中,标准差越大,生成的随机矩阵的像素值越分散。标准差越小,生成的随机矩阵的像素值越接近于均值。
可以通过调整均值和标准差的值来控制生成的随机矩阵的像素值分布。例如,当均值为0,标准差为1时,生成的随机矩阵的像素值符合标准正态分布。当均值为0,标准差为0.5时,生成的随机矩阵的像素值分布更加集中,更接近于均值。
使用SetRandNormal方法生成随机矩阵:
【代码位置:frmChapter2_1】Button22_Click
//随机矩阵
private void Button22_Click(object sender, EventArgs e)
{
Matrix<byte> matr = new Matrix<byte>(2, 4, 3);
matr.SetRandNormal(new MCvScalar(12, 33, 123), new MCvScalar(134, 12, 222));
MatrixBox1.Matrix = matr;
}
显示结果如下:

图2-23 随机矩阵
注意:SetRandNormal方法只能生成正态分布的随机矩阵,不能生成其他分布的随机矩阵。
2.2.7 最大值和最小值
Matrix类提供了MinMax方法获得矩阵内最大值、最小值以及对应的坐标位置。
【代码位置:frmChapter2_1】Button23_Click
//最大最小值
private void Button23_Click(object sender, EventArgs e)
{
byte[,] inputBytes1 = new byte[,] { { 1, 2, 3 }, { 3, 4, 9 }, { 5, 6, 7 }, { 7, 8, 9 } };
Matrix<byte> matr1 = new Matrix<byte>(inputBytes1);
MatrixBox1.Matrix = matr1;
//最小值
Double minValue;
//最大值
Double maxValue;
//最小值坐标:有多个最小值时,只返回第一个的坐标
Point minPoint;
//最大值坐标:有多个最大值时,只返回第一个的坐标
Point maxPoint;
matr1.MinMax(out minValue, out maxValue, out minPoint, out maxPoint);
TextBox1.Text += minValue + "\r\n";
TextBox1.Text += maxValue + "\r\n";
TextBox1.Text += minPoint.X + " " + minPoint.Y + "\r\n";
TextBox1.Text += maxPoint.X + " " + maxPoint.Y;
}
显示结果如下:

图2-24 最大值最小值以及对应坐标
2.2.8 类型转换
Matrix类提供了Convert方法实现矩阵类型的转换。
【代码位置:frmChapter2_1】Button24_Click
//类型转换
private void Button24_Click(object sender, EventArgs e)
{
Double[,] inputBytes1 = new Double[,] { { 1.2, 2.2, 3.3 }, { 3.3, 4.4, 5.5 }, { 5.5, 6.6, 7.7 }, { 7.7, 8.8, 9.9 } };
Matrix<Double> matr1 = new Matrix<Double>(inputBytes1);
Matrix<byte> matr2 = new Matrix<byte>(matr1.Size);
//小数转整数会四舍五入
matr2 = matr1.Convert<byte>();
MatrixBox1.Matrix = matr2;
}
显示结果如下:

图2-25 从Double转Byte
2.2.9 获得指定范围的子矩阵
Matrix类提供了Convert方法实现获得指定范围的子矩阵。其中参数是一个Rectangle类型,指定了子矩阵的开始位置、列数、行数。
【代码位置:frmChapter2_1】Button25_Click
//获得子矩阵
private void Button25_Click(object sender, EventArgs e)
{
byte[,] inputBytes1 = new byte[,] { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 }, { 10, 11, 12 } };
Matrix<byte> matr1 = new Matrix<byte>(inputBytes1);
Matrix<byte> matr2 = new Matrix<byte>(3, 2);
//获得从指定位置(1,1)开始,列数为2,行数为3的子矩阵
matr2 = matr1.GetSubRect(new Rectangle(1, 1, 2, 3));
MatrixBox1.Matrix = matr2;
}
显示结果如下:

图2-26 获得指定范围的子矩阵
2.2.10 其他方法
Matrix类还提供了以下常用方法,由于比较简单,不再这里赘述:
- Clone:复制Matrix,目标矩阵和源矩阵具有相同的行、列和通道数,元素的值也相同。
- CopyBlank:复制Matrix,目标矩阵和源矩阵具有相同的行、列和通道数,但里面元素的值都为0。
- GetCol:从源矩阵得到其中一列,并生成新的子矩阵。
- GetCols:从源矩阵得到几列的子矩阵。
- GetRow:从源矩阵得到其中一行,并生成新的子矩阵。
- GetRows:从源矩阵得到几行的子矩阵。
- RemoveCols:删除几列的后生成子矩阵。
- RemoveRows:删除几行的后生成子矩阵。
相关文章:

EmguCV学习笔记 C# 2.2 Matrix类
版权声明:本文为博主原创文章,转载请在显著位置标明本文出处以及作者网名,未经作者允许不得用于商业目的。 EmguCV学习笔记目录 Vb.net EmguCV学习笔记目录 C# 笔者的博客网址:VB.Net-CSDN博客 教程相关说明以及如何获得pdf教…...

[Windows CMD] 查看网络连接状态 netstat -na | findstr “TCP“
在 Windows 系统中,我们可以使用 netstat 命令来查看网络连接状态,并使用 findstr 命令来过滤出 TCP 和 UDP 的连接。 查看所有网络连接的状态 netstat -na netstat -na: 显示所有网络连接的状态,-n 表示显示数字地址而非域名,…...
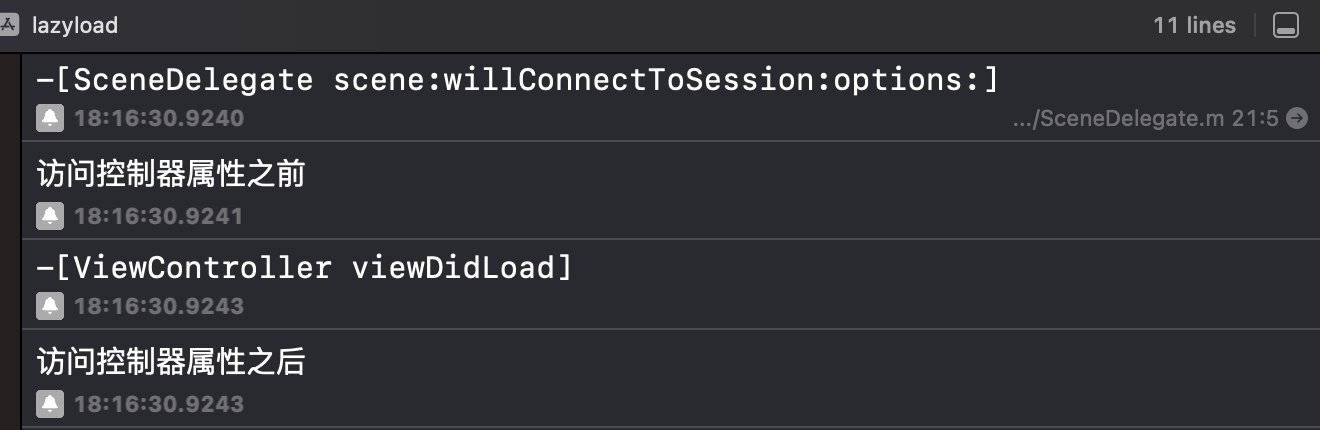
「OC」视图控制器的懒加载策略
「OC」视图控制器的懒加载策略 文章目录 「OC」视图控制器的懒加载策略懒加载懒加载的优点常见的懒加载实现方法使用懒加载的注意事项 控制器的懒加载参考资料 懒加载 懒加载(Lazy Loading)是一种设计模式,其核心思想是在需要时才进行对象的…...

android studio 中 .gitignore 文件改动后 忽略的文件夹或文件无效
问题原因:已跟踪文件的缓存问题: 如果之前已经跟踪了这些文件(即它们已经被 Git 加入到版本控制中),即使你在 .gitignore 文件中添加了忽略规则,Git 仍然会显示这些文件。你需要先从 Git 中移除这些文件&am…...
)
鸿蒙 next 实现摄像头视频预览编码(一)
鸿蒙 next 即将发布,让我们先喊3遍 遥遥领先~ 遥遥领先~ 遥遥领先~ 作为一门新的系统,本人也是刚入门学习中,如果对于一些理解有问题的,欢迎即使指出哈 首先这里要讲一下,在鸿蒙 next 中,要实现摄像头预览…...

YOLO-V3
一、概述 最大的改进就是网络结构,使其更适合小目标检测特征做的更细致,融入多持续特征图信息来预测不同规格物体先验框更丰富了,3种scale,每种3个规格,一共9种softmax改进,预测多标签任务 先验框…...

golang提案,内置 Go 错误检查函数
先来狠狠吐个槽 要吐槽 Go1 的 error ,那咱得先整明白大家为啥都猛喷它的错误处理做得不咋地。在 Go 语言里头,error 本质上其实就是个 Error 的接口: type error interface {Error() string }实际的应用场景如下: func main()…...
)
零售业务产品系统应用架构设计(三)
智慧物业依据《住房和城乡建设部等部门关于推动物业服务企业加快发展线上线下生活服务的意见建房〔2020〕99号》,推动物业管理公司广泛运用5G、互联网、物联网、云计算、大数据、区块链和人工智能等技术,建设智慧物业管理服务平台,对接城市信息模型(CIM)和城市运行管理服务…...

【GD32】从零开始学GD32单片机 | PMU电源管理单元+深度睡眠和待机例程(GD32F470ZGT6)
1. 简介 PMU电源管理单元通俗讲就是用来管理MCU的电源域的,它主要有两个功能——电压监测和低功耗管理。在GD32中一共有3个电源域——VDD/VDDA域、1.2V域和备份域。 VDD/VDDA域主要供PMU控制器、ADC、DAC等外设使用;1.2V域就是大部分外设都会使用的电源域…...

公司员工电脑桌面太乱如何解决?桌面管理软件一招解决!
“工欲善其事,必先利其器。” 在数字化管理的时代背景下,选择合适的桌面管理软件就如同为企业网络管理装上了一双慧眼。 员工的电脑桌面往往因为长时间的使用而变得杂乱无章,这不仅影响了工作效率,还可能给企业信息安全带来隐患。…...

leetcode:2119. 反转两次的数字(python3解法)
难度:简单 反转 一个整数意味着倒置它的所有位。 例如,反转 2021 得到 1202 。反转 12300 得到 321 ,不保留前导零 。 给你一个整数 num ,反转 num 得到 reversed1 ,接着反转 reversed1 得到 reversed2 。如果 reverse…...

5.vue中axios封装工程化
vue工程化中axios封装 视频演示地址:https://www.bilibili.com/video/BV121egeQEHg/?vd_source0f4eae2845bd3b24b877e4586ffda69a 通常我们封装需要封装request.js基础的发送请求工具类,再根据业务封装service类,service类是具体业务的接口…...

实验六:动态数码管实验
实验结果图,从右到左0-7,从左到右7-0,来回滚动。 硬件接线图: 具体看图,不说了,前面讲过,自己查资料就可以,资料得慢慢查,熟练就好了,不浪费时间和版面了 main.c代码 #include<reg52.h>typedef unsigned int u16; typedef unsigned char u8;#define SMG P0 …...
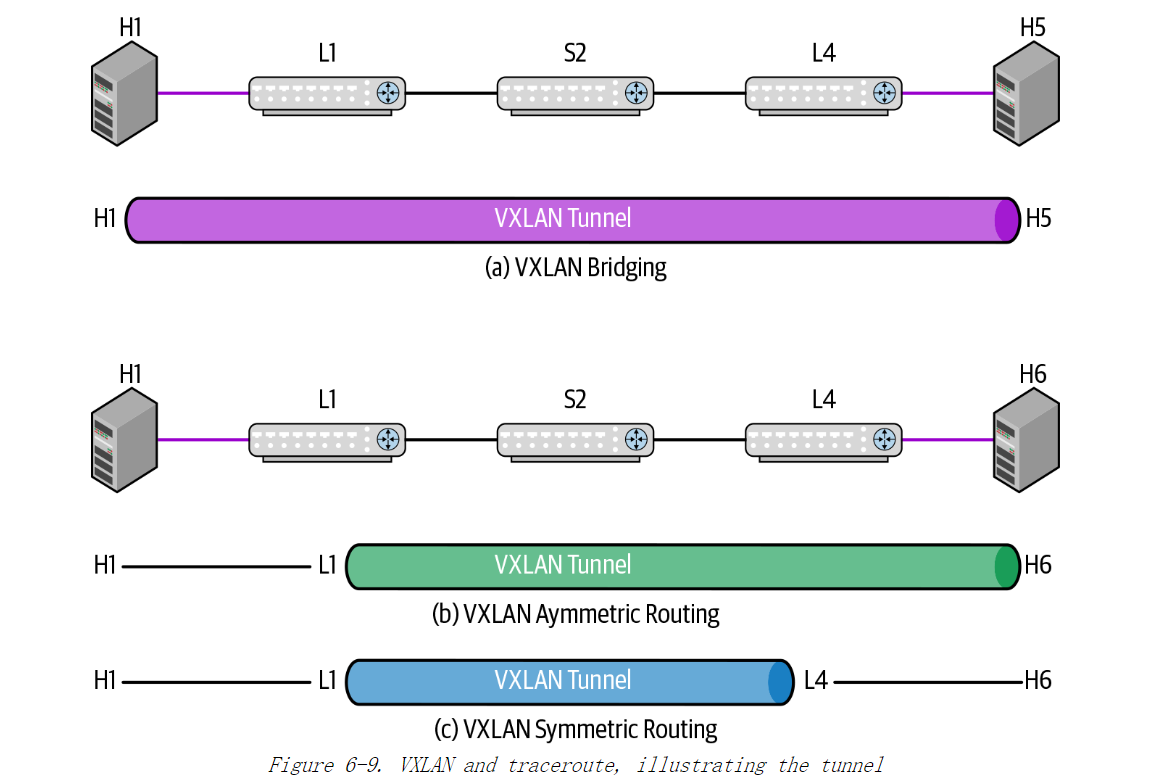
《Cloud Native Data Center Networking》(云原生数据中心网络设计)读书笔记 -- 05网络虚拟化
本章帮助网络工程师或架构师回答如下问题: 什么是网络虚拟化?网络虚拟化有哪些用途?网络虚拟化领域内有哪些不同的技术方向?网络虚拟化的控制面有哪些选择?当使用 VXLAN 时如何进行桥接和路由? 什么是网络虚拟化? 网络虚拟化可以让网络…...

奥威BI数据可视化展示:如何充分发挥数据价值
奥威BI数据可视化展示:如何充分发挥数据价值 在大数据时代,数据已成为企业最宝贵的资产之一。然而,仅仅拥有海量数据并不足以带来竞争优势,关键在于如何有效地挖掘、分析和展示这些数据,从而转化为有价值的洞察和决策…...

jenkins工具配置
上一篇(https://blog.csdn.net/abc666_666/article/details/141207741)文章我们介绍了基于docker安装jenkins的过程,本文将介绍如何配置jenkins的相关全局工具如maven、 jdk以及git等 配置的页面如下: 打开后的页面如下ÿ…...
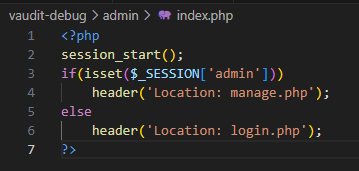
VAuditDemo文件漏洞
目录 VAuditDemo文件漏洞 一、首页文件包含漏洞 包含图片马 利用伪协议phar:// 构造shell.inc被压缩为shell.zip,然后更改shell.zip 为 shell.jpg上传 二、任意文件读取漏洞 avatar.php updateAvatar.php logCheck.php 任意文件读取漏洞利用 VAuditDemo文件…...
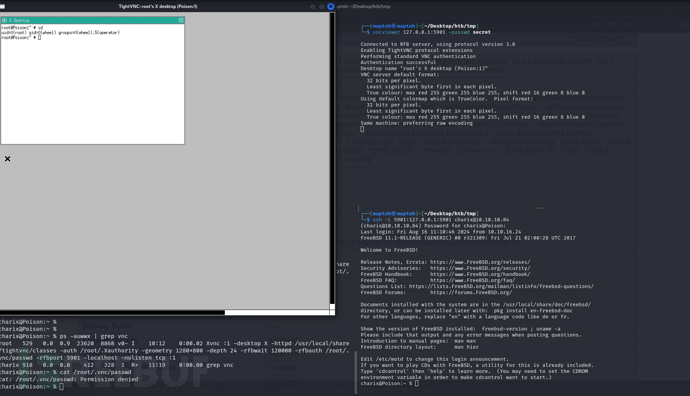
[Meachines] [Medium] poison LFI+日志投毒+VNC权限提升
信息收集 IP AddressOpening Ports10.10.10.84TCP:22,80 $ nmap -p- 10.10.10.84 --min-rate 1000 -sC -sV 22/tcp open ssh OpenSSH 7.2 (FreeBSD 20161230; protocol 2.0) | ssh-hostkey: | 2048 e3:3b:7d:3c:8f:4b:8c:f9:cd:7f:d2:3a:ce:2d:ff:bb (RSA) | 256 …...

EtherCAT运动控制器上位机开发之Python+Qt(三):PDO配置与SDO读写
ZMC408CE控制器硬件介绍 ZMC408CE是正运动推出的一款多轴高性能EtherCAT总线运动控制器,具有EtherCAT、EtherNET、RS232、CAN和U盘等通讯接口,ZMC系列运动控制器可应用于各种需要脱机或联机运行的场合。 ZMC408CE支持8轴运动控制,最多可扩展…...
)
MyBatis源码系列1(使用JDBC查询数据)
使用原生jdbc进行查询数据步骤. 1、加载驱动2、获取数据库连接3、创建Statement对象4、占位符赋值5、执行脚本6、解析结果7、关闭资源 代码示例 public class T0 {public static void main(String[] args) throws Exception {String sql "SELECT id,name FROM goods WH…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...
