数据结构——链式队列和循环队列
目录
引言
队列的定义
队列的分类
1.单链表实现
2.数组实现
队列的功能
队列的声明
1.链式队列
2.循环队列
队列的功能实现
1.队列初始化
(1)链式队列
(2)循环队列
(3)复杂度分析
2.判断队列是否为空
(1)链式队列
(2)循环队列
(3)复杂度分析
3.判断队列是否已满
(1)链式队列
(2)循环队列
(3)复杂度分析
4.返回队头元素
(1)链式队列
(2)循环队列
(3)复杂度分析
5.返回队尾元素
(1)链式队列
(2)循环队列
(3)复杂度分析
6.返回队列大小
(1)链式队列
(2)循环队列
(3)复杂度分析
7.元素入队列
(1)链式队列
(2)循环队列
(3)复杂度分析
8.元素出队列
(1)链式队列
(2)循环队列
(3)复杂度分析
9.打印队列元素
(1)链式队列
(2)循环队列
(3)复杂度分析
10.销毁队列
(1)链式队列
(2)循环队列
(3)复杂度分析
链式队列和循环队列的对比
完整代码
1.链式队列
2.循环队列
结束语
引言
在 数据结构——栈 中我们学习了栈的相关知识，今天我们接着来学习数据结构——队列。
队列的定义
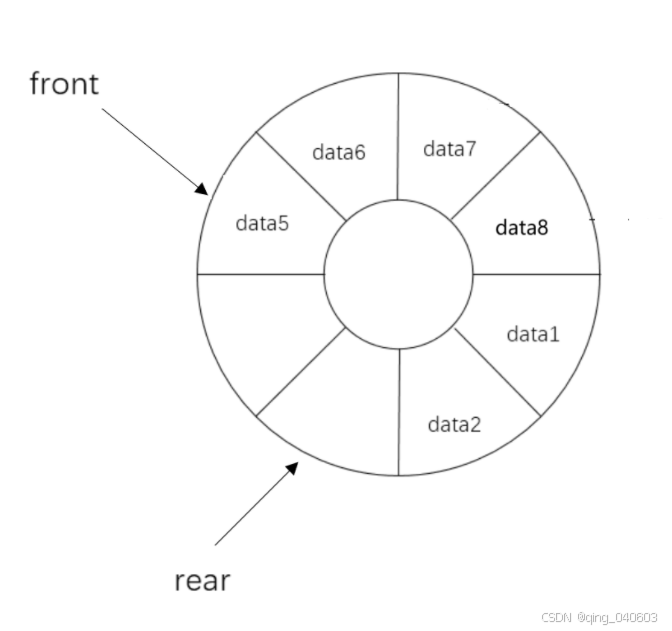
队列（Queue）是一种先进先出（FIFO, First-In-First-Out）的线性数据结构。它只允许在队列的一端（队尾）进行插入（enqueue）操作，而在另一端（队头）进行删除（dequeue）操作。这种操作方式确保了队列中元素的顺序性，即最先进入队列的元素将最先被移除。
如图所示：
队头（Front）：队头是指队列中允许删除操作的一端。也就是说，队列中的元素将按照它们被添加到队列中的顺序，从队头开始被逐一移除。
队尾（Rear）：队尾是指队列中允许插入操作的一端。新元素将被添加到队尾，以保持队列的先进先出（FIFO）特性。
队列的分类
队列与栈类似，同样可以用两种方式实现。分别是单链表和数组。接下来我们来分析一下如何使用两种方法实现队列。
1.单链表实现
我们可以将链表的头节点与尾节点分别作为队列的队首与队尾，这样我们就能用两个指针来对其进行操作。
如下图所示：
2.数组实现
问题一：
在使用数组实现队列时，可能会出现“假溢出”的情况。这是因为数组的头部和尾部是固定的，当队列的尾部达到数组的末尾时，即使数组的头部还有很多空闲空间，也无法再向队列中添加新元素。这种情况下，队列虽然看起来是满的，但实际上还有很多空间没有被利用。
解决方法：
我们可以将数组相接变成循环数组。
问题二：
变成循环数组又会出现新的问题：当队首与队尾下标都指向同一个节点时，这个队列是空还是满呢？
解决方法：
多使用一个空间便于我们区分队空和队满。若队列不为空，让队尾下标指向队尾的下一个位置。我们约定以队头指针在队尾指针的下一位置作为队满的标志，即Queue->rear+1=Queue->front。
如下图所示：
队满状态：
队列的功能
1.队列的初始化。
2.判断队列是否为空。
3.判断队列是否已满。
4.返回队头元素。
5.返回队尾元素
6.返回队列的大小。
7.元素入队列。
8.元素出队列。
9.打印队列的元素。
10.销毁队列。
队列的声明
1.链式队列
typedef int QDataType;typedef struct QueueNode
{struct QueueNode* next;QDataType val;
}QNode;typedef struct Queue
{QNode* front;QNode* rear;int size;
}Queue;2.循环队列
typedef int QDataType;#define MAXSIZE 30 //定义队列的最大值
typedef struct
{QDataType* data;int front; //头指针int rear; //尾指针
}Queue;队列的功能实现
1.队列初始化
给队列中的各个元素给定值，以免出现随机值。
(1)链式队列
//初始化
void QueueInit(Queue* q)
{assert(q);q->front = NULL;q->rear = NULL;q->size = 0;
}(2)循环队列
//初始化
void QueueInit(Queue* q)
{// 为队列的数据存储空间分配内存。q->data = (QDataType*)malloc(sizeof(QDataType) * MAXSIZE);if (q->data == NULL){perror("malloc fail:");return;}// 初始化队首和队尾指针为0，表示队列为空q->front = q->rear = 0;
}
(3)复杂度分析
时间复杂度：由于链式队列和循环队列花费时间都是一个常数，因此时间复杂度为O(1)。
空间复杂度：由于链式队列花费的是一个固定大小的空间，因此空间复杂度为O(1)。循环队列需要开辟整个队列的大小，因此空间复杂度为O(N)。
2.判断队列是否为空
(1)链式队列
判断size是否为0即可。
代码如下：
//判断队列是否为空
bool QueueEmpty(Queue* q)
{assert(q);return q->size == 0;
}(2)循环队列
判断front是否等于rear即可。
代码如下：
//判断队列是否为空
bool QueueEmpty(Queue* q)
{assert(q);return q->front == q->rear;
}(3)复杂度分析
时间复杂度：由于链式队列和循环队列花费时间都是一个常数，因此时间复杂度为O(1)。
空间复杂度：由于链式队列和循环队列花费空间都是一个常数，因此空间复杂度为O(1)。
3.判断队列是否已满
(1)链式队列
链式队列不需要判断队列是否已满。
(2)循环队列
循环队列判断是否已满需要进行一些特殊处理。
代码如下：
//判断队列是否已满
bool QueueFull(Queue* q)
{assert(q);// 取模操作是避免越界return q->front == (q->rear + 1) % MAXSIZE;
}(3)复杂度分析
时间复杂度：由于循环队列花费时间是一个常数，因此时间复杂度为O(1)。
空间复杂度：循环队列花费的是一个固定大小的空间，所以空间复杂度为O(1)。
4.返回队头元素
(1)链式队列
//读取队头数据
QDataType QueueFront(Queue* q)
{assert(q);assert(q->front);return q->front->val;
}(2)循环队列
//读取队头数据
QDataType QueueFront(Queue* q)
{assert(q);assert(!QueueEmpty(q));return q->data[q->front];
}(3)复杂度分析
时间复杂度：由于链式队列和循环队列花费时间都是一个常数，因此时间复杂度为O(1)。
空间复杂度：由于链式队列和循环队列花费空间都是一个常数，因此空间复杂度为O(1)。
5.返回队尾元素
(1)链式队列
//读取队尾数据
QDataType QueueBack(Queue* q)
{assert(q);assert(q->rear);return q->rear->val;
}(2)循环队列
//读取队尾数据
QDataType QueueBack(Queue* q)
{assert(q);assert(!QueueEmpty(q));// 当rear为0时，rear-1会导致负数索引，这在数组中是无效的 // 通过加上MAXSIZE并取模MAXSIZE，我们可以确保索引始终在有效范围内 // 这里(q->rear - 1 + MAXSIZE) % MAXSIZE计算的是队尾元素的索引return q->data[(q->rear - 1 + MAXSIZE) % MAXSIZE];
}(3)复杂度分析
时间复杂度：由于链式队列和循环队列花费时间都是一个常数，因此时间复杂度为O(1)。
空间复杂度：由于链式队列和循环队列花费空间都是一个常数，因此空间复杂度为O(1)。
6.返回队列大小
(1)链式队列
链式队列求队列大小很简单，直接返回size即可。
代码如下：
//统计队列数据个数
int QueueSize(Queue* q)
{assert(q);return q->size;
}(2)循环队列
我们来分析一下：
像这个可以使用rear-front求出队列的大小。但是要知道，这是个循环队列，rear时=是可以跑到front之后的，如下图所示：
解决方法：rear减去front之后加个MAXSIZE就好了。
代码如下：
//统计队列数据个数
int QueueSize(Queue* q)
{assert(q);return (q->rear - q->front + MAXSIZE) % MAXSIZE;
}(3)复杂度分析
时间复杂度：由于链式队列和循环队列花费时间都是一个常数，因此时间复杂度为O(1)。
空间复杂度：由于链式队列和循环队列花费空间都是一个常数，因此空间复杂度为O(1)。
7.元素入队列
(1)链式队列
链式队列元素入队需要判断队列是否为空的情况。
代码如下：
//队尾插入
void QueuePush(Queue* q, QDataType x)
{assert(q);QNode* newNode = (QNode*)malloc(sizeof(QNode));if (newNode == NULL){perror("malloc fail");return;}newNode->next = NULL;newNode->val = x;// 如果队列为空 if (q->rear == NULL){// 新节点既是队首也是队尾q->front = q->rear = newNode;}else{// 将当前队尾节点的next指向新节点q->rear->next = newNode;// 更新队尾指针为新节点q->rear = newNode;}q->size++;
}(2)循环队列
取模操作不能少，确保不会越界。
//队尾插入
void QueuePush(Queue* q, QDataType x)
{assert(q);if (QueueFull){printf("队列已满\n");return;}q->data[q->rear] = x;// rear指针向后移动// (q->rear + 1) % MAXSIZE这段代码// 确保了rear指针的值始终在0到MAXSIZE-1的范围内循环q->rear = (q->rear + 1) % MAXSIZE;
}(3)复杂度分析
时间复杂度：由于链式队列和循环队列花费时间都是一个常数，因此时间复杂度为O(1)。
空间复杂度：由于链式队列和循环队列花费空间都是一个常数，因此空间复杂度为O(1)。
8.元素出队列
(1)链式队列
//队头删除
void QueuePop(Queue* q)
{assert(q);assert(q->size != 0);// 检查队列中是否只有一个节点if (q->front->next == NULL){free(q->front);// 队列变为空，队首和队尾指针都设置为NULLq->front = q->rear = NULL;}// 多个节点else{// 保存下一个节点的指针QNode* next = q->front->next;// 释放队首节点free(q->front);// 更新队首指针为下一个节点q->front = next;}q->size--;
}(2)循环队列
//队头删除
void QueuePop(Queue* q)
{assert(q);assert(!QueueEmpty(q));// front指针向后移动// (q->front + 1) % MAXSIZE这段代码// 确保了front指针的值始终在0到MAXSIZE-1的范围内循环q->front = (q->front + 1) % MAXSIZE;
}(3)复杂度分析
时间复杂度：由于链式队列和循环队列花费时间都是一个常数，因此时间复杂度为O(1)。
空间复杂度：由于链式队列和循环队列花费空间都是一个常数，因此空间复杂度为O(1)。
9.打印队列元素
(1)链式队列
//打印队列元素
void QueuePrint(Queue* q)
{assert(q);QNode* cur = q->front;QNode* tail = q->rear;printf("队头->");while (cur != tail->next){printf("%d->", cur->val);cur = cur->val;}printf("队尾\n");
}(2)循环队列
//打印队列元素
void QueuePrint(Queue* q)
{assert(q);int cur = q->front;printf("队头->");while (cur != q->rear){printf("%d->", q->data[cur]);// 避免越界cur = (cur + 1) % MAXSIZE;}printf("队尾\n");
}(3)复杂度分析
时间复杂度：由于链式队列和循环队列都需要遍历整个队列，因此时间复杂度为O(n)。
空间复杂度：由于链式队列和循环队列花费空间都是一个常数，因此空间复杂度为O(1)。
10.销毁队列
(1)链式队列
//销毁
void QueueDestroy(Queue* q)
{assert(q);QNode* cur = q->front;while (cur){QNode* next = cur->next;free(cur);cur = next;}q->front = q->rear = NULL;q->size = 0;
}(2)循环队列
//销毁
void QueueDestroy(Queue* q)
{assert(q);free(q->data);q->data = NULL;q->front = q->rear = 0;
}(3)复杂度分析
时间复杂度：由于链式队列需要遍历整个队列，因此时间复杂度为O(n)。循环队列花费时间是一个常数，因此时间复杂度为O(1)。
空间复杂度：由于链式队列和循环队列花费空间都是一个常数，因此空间复杂度为O(1)。
链式队列和循环队列的对比
| 链式列表 | 循环列表 | |
| 数据结构 | 使用链表实现，队列中的每个元素都是一个链表节点，节点之间通过指针相连 | 使用数组实现，但在逻辑上将数组的头尾相连，形成一个环形结构。 |
| 内存管理 | 出队或清空队列时需要释放链表节点的内存 | 无需手动释放内存，因为队列元素存储在数组中，数组的内存由系统自动管理 |
| 时间效率 | 由于使用头指针与尾指针，因此链式队的出队与入队的时间都相对较小 | 循环队列是基于数组实现的，支持下标的随机访问，所以时间消耗并不大 |
| 空间效率 | 空间使用灵活，可以根据需要动态地增加或减少内存分配 | 空间使用相对固定，需要预先定义最大容量。如果队列的实际大小远小于最大容量，则会造成空间浪费 |
完整代码
1.链式队列
Queue.h
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int QDataType;typedef struct QueueNode
{struct QueueNode* next;QDataType val;
}QNode;typedef struct Queue
{QNode* front;QNode* rear;int size;
}Queue;//初始化
void QueueInit(Queue* q);
//销毁
void QueueDestroy(Queue* q);//队尾插入
void QueuePush(Queue* q, QDataType x);
//队头删除
void QueuePop(Queue* q);//读取队头数据
QDataType QueueFront(Queue* q);
//读取队尾数据
QDataType QueueBack(Queue* q);//统计队列数据个数
int QueueSize(Queue* q);
//判断队列是否为空
bool QueueEmpty(Queue* q);//打印队列元素
void QueuePrint(Queue* q);
Queue.c
#define _CRT_SECURE_NO_WARNINGS 1#include"Queue.h"//初始化
void QueueInit(Queue* q)
{assert(q);q->front = NULL;q->rear = NULL;q->size = 0;
}//销毁
void QueueDestroy(Queue* q)
{assert(q);QNode* cur = q->front;while (cur){QNode* next = cur->next;free(cur);cur = next;}q->front = q->rear = NULL;q->size = 0;
}//队尾插入
void QueuePush(Queue* q, QDataType x)
{assert(q);QNode* newNode = (QNode*)malloc(sizeof(QNode));if (newNode == NULL){perror("malloc fail");return;}newNode->next = NULL;newNode->val = x;// 如果队列为空 if (q->rear == NULL){// 新节点既是队首也是队尾q->front = q->rear = newNode;}else{// 将当前队尾节点的next指向新节点q->rear->next = newNode;// 更新队尾指针为新节点q->rear = newNode;}q->size++;
}//队头删除
void QueuePop(Queue* q)
{assert(q);assert(q->size != 0);// 检查队列中是否只有一个节点if (q->front->next == NULL){free(q->front);// 队列变为空，队首和队尾指针都设置为NULLq->front = q->rear = NULL;}// 多个节点else{// 保存下一个节点的指针QNode* next = q->front->next;// 释放队首节点free(q->front);// 更新队首指针为下一个节点q->front = next;}q->size--;
}//读取队头数据
QDataType QueueFront(Queue* q)
{assert(q);assert(q->front);return q->front->val;
}//读取队尾数据
QDataType QueueBack(Queue* q)
{assert(q);assert(q->rear);return q->rear->val;
}//统计队列数据个数
int QueueSize(Queue* q)
{assert(q);return q->size;
}//判断队列是否为空
bool QueueEmpty(Queue* q)
{assert(q);return q->size == 0;
}//打印队列元素
void QueuePrint(Queue* q)
{assert(q);QNode* cur = q->front;QNode* tail = q->rear;printf("队头->");while (cur != tail->next){printf("%d->", cur->val);cur = cur->val;}printf("队尾\n");
}2.循环队列
Queue.h
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>typedef int QDataType;#define MAXSIZE 30
typedef struct
{QDataType* data;int front;int rear;
}Queue;//初始化
void QueueInit(Queue* q);
//销毁
void QueueDestroy(Queue* q);//队尾插入
void QueuePush(Queue* q, QDataType x);
//队头删除
void QueuePop(Queue* q);//读取队头数据
QDataType QueueFront(Queue* q);
//读取队尾数据
QDataType QueueBack(Queue* q);//统计队列数据个数
int QueueSize(Queue* q);
//判断队列是否为空
bool QueueEmpty(Queue* q);//打印队列元素
void QueuePrint(Queue* q);//判断队列是否已满
bool QueueFull(Queue* q);
Queue.h
#define _CRT_SECURE_NO_WARNINGS 1
#include"Queue.h"//初始化
void QueueInit(Queue* q)
{// 为队列的数据存储空间分配内存。q->data = (QDataType*)malloc(sizeof(QDataType) * MAXSIZE);if (q->data == NULL){perror("malloc fail:");return;}// 初始化队首和队尾指针为0，表示队列为空q->front = q->rear = 0;
}//销毁
void QueueDestroy(Queue* q)
{assert(q);free(q->data);q->data = NULL;q->front = q->rear = 0;
}//队尾插入
void QueuePush(Queue* q, QDataType x)
{assert(q);if (QueueFull(q)){printf("队列已满\n");return;}q->data[q->rear] = x;// rear指针向后移动// (q->rear + 1) % MAXSIZE这段代码// 确保了rear指针的值始终在0到MAXSIZE-1的范围内循环q->rear = (q->rear + 1) % MAXSIZE;
}//队头删除
void QueuePop(Queue* q)
{assert(q);assert(!QueueEmpty(q));// front指针向后移动// (q->front + 1) % MAXSIZE这段代码// 确保了front指针的值始终在0到MAXSIZE-1的范围内循环q->front = (q->front + 1) % MAXSIZE;
}//读取队头数据
QDataType QueueFront(Queue* q)
{assert(q);assert(!QueueEmpty(q));return q->data[q->front];
}
//读取队尾数据
QDataType QueueBack(Queue* q)
{assert(q);assert(!QueueEmpty(q));// 当rear为0时，rear-1会导致负数索引，这在数组中是无效的 // 通过加上MAXSIZE并取模MAXSIZE，我们可以确保索引始终在有效范围内 // 这里(q->rear - 1 + MAXSIZE) % MAXSIZE计算的是队尾元素的索引return q->data[(q->rear - 1 + MAXSIZE) % MAXSIZE];
}//统计队列数据个数
int QueueSize(Queue* q)
{assert(q);return (q->rear - q->front + MAXSIZE) % MAXSIZE;
}//判断队列是否为空
bool QueueEmpty(Queue* q)
{assert(q);return q->front == q->rear;
}//判断队列是否已满
bool QueueFull(Queue* q)
{assert(q);return q->front == (q->rear + 1) % MAXSIZE;
}//打印队列元素
void QueuePrint(Queue* q)
{assert(q);int cur = q->front;printf("队头->");while (cur != q->rear){printf("%d->", q->data[cur]);// 避免越界cur = (cur + 1) % MAXSIZE;}printf("队尾\n");
}结束语
本篇博客大致介绍了数据结构——队列的内容。
感谢每位能点进来阅读的大佬们！！！
十分感谢！！！
求点赞收藏关注！！！
相关文章：
数据结构——链式队列和循环队列
目录 引言 队列的定义 队列的分类 1.单链表实现 2.数组实现 队列的功能 队列的声明 1.链式队列 2.循环队列 队列的功能实现 1.队列初始化 (1)链式队列 (2)循环队列 (3)复杂度分析 2.判断队列是否为空 (1)链式队列 (2)循环队列 (3)复杂度分析 3.判断队列是否…...
数据库死锁解决方法，学费了吗？
避免死锁：尽量设计良好的数据库结构，避免出现死锁的情况。可以使用合适的事务隔离级别，以及良好的并发控制策略。 死锁检测和回滚：当检测到死锁时，可以使用死锁检测算法来确定死锁的存在，并回滚其中一个或…...
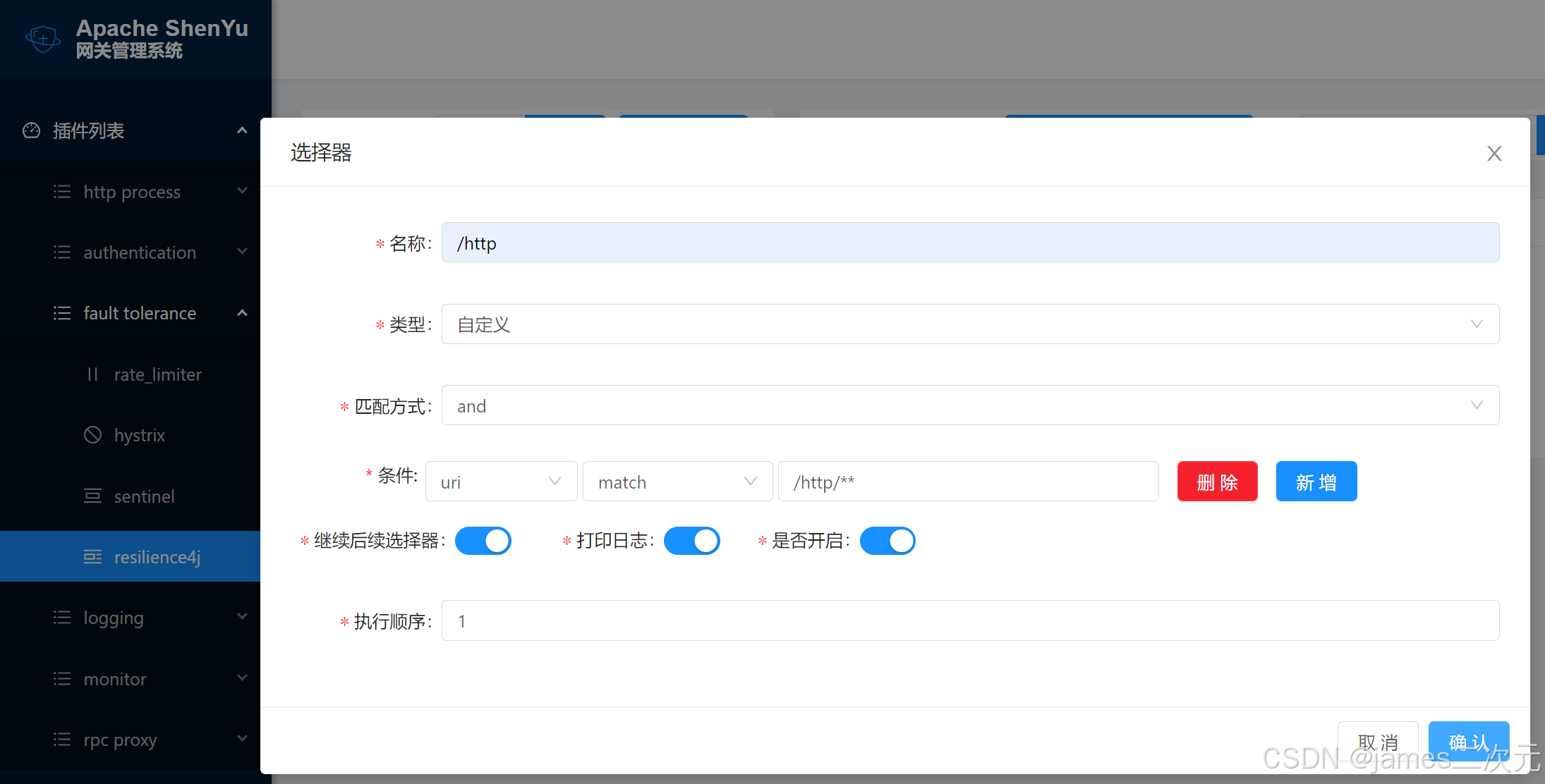
API网关之Apache ShenYu
Apache ShenYu（原名Soul）是一个开源的API网关，旨在支持高性能、跨语言和云原生架构。它为管理和控制客户端与服务之间的数据流提供了一种高效且可扩展的解决方案。 文档见 Apache ShenYu 介绍 | Apache ShenYu 以下是Apache ShenYu的详细介…...
ECMA Script 6
文章目录 DOM (Document Object Model)BOM (Browser Object Model) let 和 const 命令constObject.freeze方法跨模块常量全局对象的属性 变量的结构赋值数组结构赋值对象解构赋值字符串解构赋值数值和布尔值的解构赋值函数参数解构赋值圆括号的问题 解构赋值的用途 字符串的扩展…...
如何在不破产的情况下训练AI模型
在当今的人工智能领域，训练复杂的AI模型——特别是大型语言模型（LLM）——需要巨大的算力支持。对于许多中小型企业来说，高昂的成本常常成为一个难以逾越的障碍。然而，通过采用一些策略和最佳实践，即使是在资源有限的情况下，也能有效地训练出高质量的AI模型。本文将介绍几…...
常用开发组件Docker部署保姆级教程
说明 本文总结了一些常用组件的Docker启动命令及过程，在开发过程中只需花费数分钟下载和配置即可完美使用这些服务。 Mysql MySQL 是一种开源关系数据库管理系统（RDBMS），目前由 Oracle 公司维护。MySQL 以其高性能、可靠性和易用…...
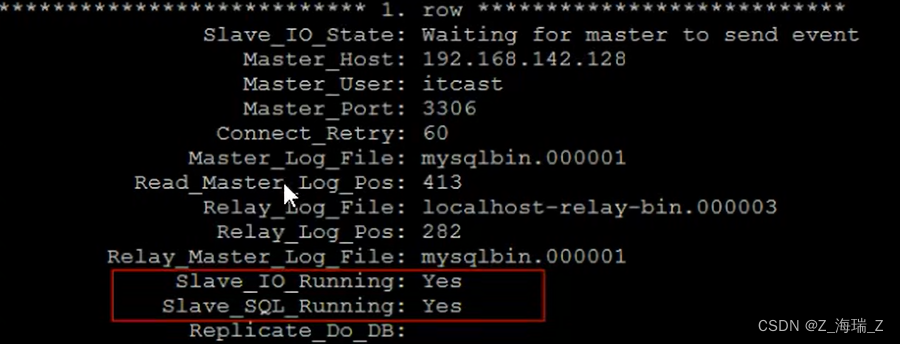
MySql高级视频笔记
索引 索引 : 是帮助MySql高效查询数据的数据结构 优势&劣势 优势: 提高数据检索的效率, 降低数据库的IO成本通过索引列队数据进行排序, 降低数据的排序成本, 降低CPU的消耗 劣势: 索引维护了主键信息, 并指向表中数据记录, 也是占用磁盘空间的索引提高了查询效率, 但索引也…...
二十二、状态模式
文章目录 1 基本介绍2 案例2.1 Season 接口2.2 Spring 类2.3 Summer 类2.4 Autumn 类2.5 Winter 类2.6 Person 类2.7 Client 类2.8 Client 类的运行结果2.9 总结 3 各角色之间的关系3.1 角色3.1.1 State ( 状态 )3.1.2 ConcreteState ( 具体的状态 )3.1.3 Context ( 上下文 )3.…...
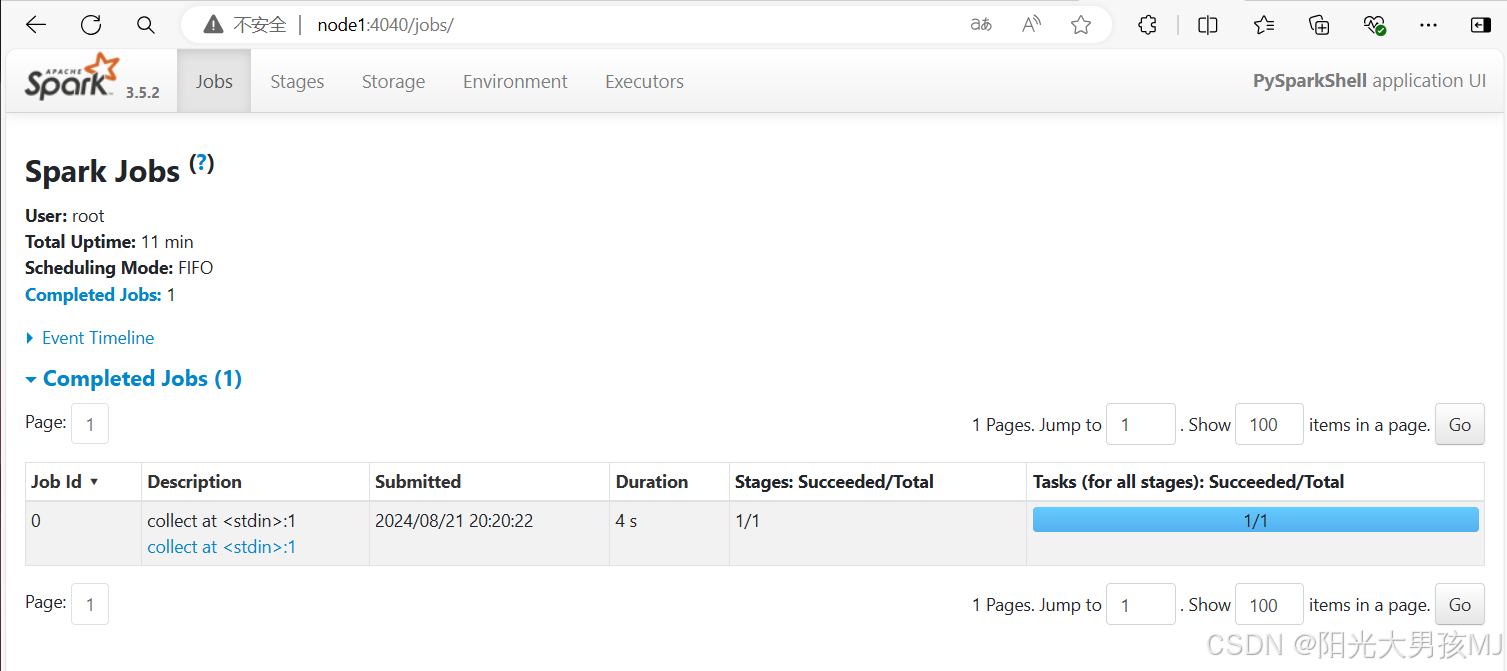
Spark环境搭建-Local
目录 Local下的角色分布： Anaconda On Linux 安装 (单台服务器) 1.下载安装 2.国内源 下载Spark安装包 1.下载 2.解压 3.环境变量 测试 监控 Local下的角色分布： 资源管理： Master：Local进程本身 Worker：L…...
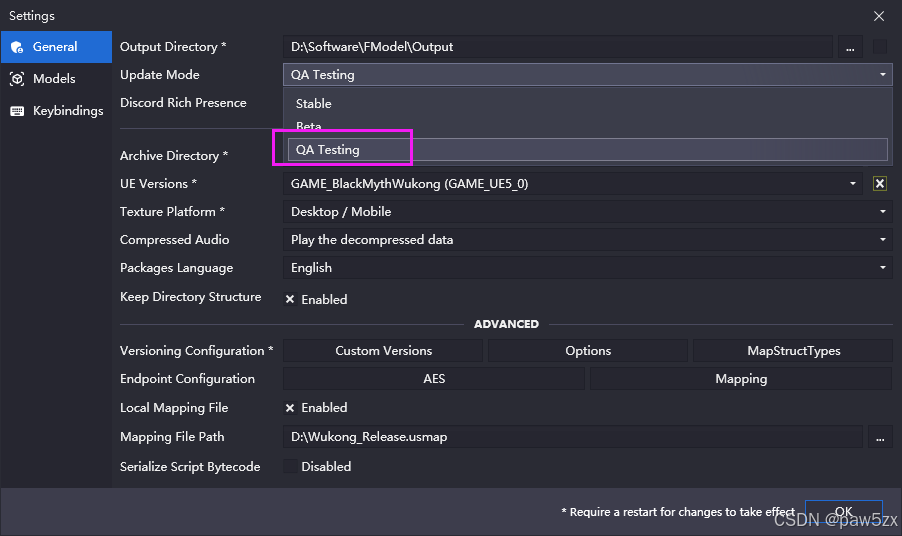
使用FModel提取黑神话悟空的资产
使用FModel提取黑神话悟空的资产 前言设置效果展示闲聊可能遇到的问题没有相应的UE引擎版本选项 前言 黑神话悟空昨天上线了，解个包looklook。 本文内容比较简洁，仅介绍解包黑神话所需的专项配置，关于FModel的基础使用流程，请见…...
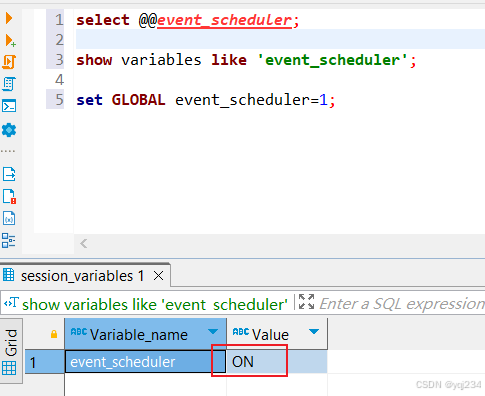
MYSQL定时任务使用手册
开发和管理数据库时，经常需要定时执行某些任务，比如每天备份数据库、每周统计报表等。MySQL提供了一个非常有用的工具，即事件调度器（Event Scheduler），可以帮助我们实现定时任务调度的功能。本文将介绍如何…...
SAP 预扣税配置步骤文档【Withholding Tax]
1. 配置预扣税的基本概念 预扣税是对某些支付进行扣除的税，可能适用于各种财务交易（例如，供应商支付、股息支付等）。预扣税通常包括几种类型，如个人所得税、企业所得税和其他税务种类。 2. 配置步骤 以下是一般的预…...
Ubuntu ssh配置
下面给出配置和使用ubuntu ssh的指南。 环境 Ubuntu22.04 安装Install sudo apt update && sudo apt upgrade sudo apt install openssh-server使用start service ssh status sudo systemctl enable --now ssh sudo ufw allow ssh连接Connect search "conn…...
Spring Boot OAuth2.0应用
本文展示Spring Boot中，新版本OAuth2.0的简单实现，版本信息： spring-boot 2.7.10 spring-security-oauth2-authorization-server 0.4.0 spring-security-oauth2-client 5.7.7 spring-boot-starter-oauth2-resource-server 2.7.10展示三个服务…...
Java | Leetcode Java题解之第363题矩形区域不超过K的最大数值和
题目： 题解： class Solution {public int maxSumSubmatrix(int[][] matrix, int k) {int ans Integer.MIN_VALUE;int m matrix.length, n matrix[0].length;for (int i 0; i < m; i) { // 枚举上边界int[] sum new int[n];for (int j i; j <…...
AI作画提示词（Prompts）工程：技巧与最佳实践
在人工智能领域，AI作画已成为一个令人兴奋的创新点，它结合了艺术与科技，创造出令人惊叹的视觉作品。本文将探讨在使用AI作画时的提示词工程，提供技巧与最佳实践。 理解AI作画 AI作画通常依赖于深度学习模型，尤其是生成…...
leetcode滑动窗口问题
想成功先发疯，不顾一切向前冲。 第一种 定长滑动窗口 . - 力扣（LeetCode）1456.定长子串中的元音的最大数目. - 力扣（LeetCode） No.1 定长滑窗套路 我总结成三步：入-更新-出。 1. 入：下标为…...
QT 控件使用案例
常用控件 表单 按钮 Push Button 命令按钮。Tool Button：工具按钮。Radio Button：单选按钮。Check Box：复选框按钮。Command Link Button：命令链接按钮。Dialog Button Box：按钮盒。 容器组控件(Containers) Group Box…...
【MySQL 10】表的内外连接 (带思维导图)
文章目录 🌈 一、内连接⭐ 0. 准备工作⭐ 1. 隐式内连接⭐ 2. 显式内连接 🌈 二、外连接⭐ 0. 准备工作⭐ 1. 左外连接⭐ 2. 右外连接 🌈 一、内连接 内连接实际上就是利用 where 子句对两张表形成的笛卡儿积进行筛选，之前所有的…...
【C语言】：与文件通信
1.文件是什么？ 文件通常是在磁盘或固态硬盘上的一段已命名的存储区。C语言把文件看成一系列连续的字节，每个字节都能被单独的读取。这与UNIX环境中（C的 发源地）的文件结构相对应。由于其他环境中可能无法完全对应这个模型&#x…...
详解与优化实践)
ARM AArch32性能监控寄存器(PMU)详解与优化实践
1. ARM AArch32性能监控寄存器深度解析在嵌入式系统和移动计算领域，性能监控单元(PMU)是处理器微架构中至关重要的组成部分。作为一位长期从事ARM架构开发的工程师，我经常需要深入理解PMU寄存器的工作原理，以优化关键代码段的执行效率。本文将…...
OpenRegistry私有镜像仓库：轻量部署与生产实践指南
1. 项目概述：一个面向容器生态的私有镜像仓库如果你在团队里负责过容器化应用的部署和维护，大概率遇到过镜像管理的痛点。从Docker Hub拉取公共镜像，速度慢不说，安全性和稳定性也完全不可控；把所有镜像都放在开发者的本…...
构建企业级安全运维体系：从SSH堡垒机到自动化管控平台
1. 项目概述：从“GMSSH/GMClaw”看现代远程访问与管理的演进最近在和一些做基础设施和运维的朋友交流时，他们频繁提到一个组合词：“GMSSH/GMClaw”。乍一听，这像是一个内部代号或者某个新工具的名字。深入聊下去才发现，…...
鲲鹏超节点系统应用创新竞争力
鲲鹏超节点通过灵衢互联，打破传统的服务器边界，实现以数据为中心的全互联架构，为AI infra而生，具备大带宽、低时延、统一编址、内存语义、内存借用、内存共享、对等互联等关键能力，灵衢软件全面开源开放，让…...
免费解锁Adobe全家桶！Adobe GenP 3.0终极指南让你告别订阅费
免费解锁Adobe全家桶！Adobe GenP 3.0终极指南让你告别订阅费 【免费下载链接】Adobe-GenP Adobe CC 2019/2020/2021/2022/2023 GenP Universal Patch 3.0 项目地址: https://gitcode.com/gh_mirrors/ad/Adobe-GenP 还在为Adobe Creative Cloud的高昂订阅费用…...
iMeta | 伦敦国王学院量化系统生物学组-解析肝硬化中口腔-肠道转移细菌与宿主互作
点击蓝字 关注我们整合宿主–微生物组建模揭示了口腔–肠道微生物转移在晚期肝硬化中的潜在作用iMeta主页：http://www.imeta.science研究论文● 期刊: iMeta (IF 33.2,中科院双一区Top)● 英文题目: Integrative host-microbiome modelling uncovers the implicatio…...
Freewall跨浏览器兼容性：解决IE8+布局问题的完整方案
Freewall跨浏览器兼容性：解决IE8布局问题的完整方案 【免费下载链接】freewall kombai/freewall: Freewall 是一个灵活、响应式的网格布局引擎，可用于创建具有自适应布局功能的网页或应用组件，尤其适合于图片墙、瀑布流布局等场景。 项目地…...
BilibiliDown：三步搞定B站无损音频提取，构建你的专属音乐库
BilibiliDown：三步搞定B站无损音频提取，构建你的专属音乐库 【免费下载链接】BilibiliDown (GUI-多平台支持) B站 哔哩哔哩 视频下载器。支持稍后再看、收藏夹、UP主视频批量下载|Bilibili Video Downloader 😳 项目地址: https://gitcode.…...
从硬开关到软开关：推挽谐振变换器原理与PSIM仿真实战
1. 从经典到谐振：为什么我们需要推挽变换器？在电源设计的工具箱里，推挽变换器（Push-Pull Converter）绝对算得上是一位“老将”。它的核心思想非常直观：利用一个带中心抽头的变压器，让两个开关管…...
如何快速掌握AMD处理器调试工具：从新手到专家的完整指南
如何快速掌握AMD处理器调试工具：从新手到专家的完整指南 【免费下载链接】SMUDebugTool A dedicated tool to help write/read various parameters of Ryzen-based systems, such as manual overclock, SMU, PCI, CPUID, MSR and Power Table. 项目地址: https://…...