协方差详解及在日常生活中的应用实例——天气温度与冰淇淋销量的关系
协方差详解及在日常生活中的应用实例——天气温度与冰淇淋销量的关系
文章目录
- 协方差详解及在日常生活中的应用实例——天气温度与冰淇淋销量的关系
- 引言
- 协方差的概念与背景
- 数学公式推导
- 实例背景
- 数据收集
- 计算过程
- 结果解释
- 计算相关系数
- 为什么使用协方差?
- 结论
- 商业启示
引言
在日常生活中,我们经常会遇到需要分析两个变量之间关系的情况。其中一个重要的统计量就是协方差,它可以帮助我们理解两个变量之间的线性关系方向和强度。本文将通过一个具体的实例——天气温度与冰淇淋销量之间的关系——来探讨协方差的应用,并详细介绍协方差的概念、背景、数学公式推导等内容。此外,我们还将讨论与协方差类似的概念,并探讨何时使用协方差以及为什么选择使用协方差。
协方差的概念与背景
定义:协方差是一个统计量,用于衡量两个变量之间线性关系的方向和强度。如果两个变量的值倾向于同时增加或减少,则它们具有正协方差;如果一个变量增加而另一个变量减少,则它们具有负协方差。协方差的值越大,表示两个变量之间的线性关系越强。
背景:在数据分析和统计建模中,了解两个变量间的关系是非常重要的。协方差提供了一种量化这种关系的方法。例如,在金融领域,协方差可以帮助投资者了解不同资产价格变动的趋势是否一致,这对于构建有效的投资组合非常重要。在本例中,我们将利用协方差来探索天气温度与冰淇淋销量之间的关系。
数学公式推导
设有两个随机变量 X X X 和 Y Y Y,它们分别有一组观测值 x 1 , x 2 , … , x n x_1, x_2, \ldots, x_n x1,x2,…,xn 和 y 1 , y 2 , … , y n y_1, y_2, \ldots, y_n y1,y2,…,yn。则 X X X 和 Y Y Y 的协方差定义为:
Cov ( X , Y ) = 1 n ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) \text{Cov}(X, Y) = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y}) Cov(X,Y)=n1i=1∑n(xi−xˉ)(yi−yˉ)
其中, x ˉ \bar{x} xˉ 和 y ˉ \bar{y} yˉ 分别表示 X X X 和 Y Y Y 的样本均值。
这个公式可以分解成以下几个步骤:
-
计算均值:对于每个变量,计算其样本均值。
- x ˉ = 1 n ∑ i = 1 n x i \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i xˉ=n1∑i=1nxi
- y ˉ = 1 n ∑ i = 1 n y i \bar{y} = \frac{1}{n} \sum_{i=1}^{n} y_i yˉ=n1∑i=1nyi
-
计算偏差:对于每个数据点 ( x i , y i ) (x_i, y_i) (xi,yi),计算其与相应变量均值的偏差。
- d x ( i ) = x i − x ˉ d_x(i) = x_i - \bar{x} dx(i)=xi−xˉ
- d y ( i ) = y i − y ˉ d_y(i) = y_i - \bar{y} dy(i)=yi−yˉ
-
计算乘积并求和:将每个数据点的偏差相乘,然后求和。
- p i = d x ( i ) ⋅ d y ( i ) p_i = d_x(i) \cdot d_y(i) pi=dx(i)⋅dy(i)
- Cov ( X , Y ) = 1 n ∑ i = 1 n p i \text{Cov}(X, Y) = \frac{1}{n} \sum_{i=1}^{n} p_i Cov(X,Y)=n1∑i=1npi
实例背景
假设你经营着一家冰淇淋店,并希望了解天气温度与冰淇淋销量之间的关系。通过收集一个月的数据,我们可以分析这两者之间的相关性,以便更好地规划库存和调整销售策略。
数据收集
我们收集了连续30天的温度(以摄氏度为单位)和对应的冰淇淋销量(以销售数量为单位)数据:
| 天数 | 温度 (°C) | 冰淇淋销量 |
|---|---|---|
| 1 | 20 | 100 |
| 2 | 22 | 120 |
| 3 | 25 | 140 |
| 4 | 26 | 150 |
| 5 | 23 | 125 |
| 6 | 24 | 130 |
| 7 | 27 | 160 |
| 8 | 28 | 170 |
| 9 | 29 | 180 |
| 10 | 30 | 190 |
| 11 | 26 | 155 |
| 12 | 27 | 165 |
| 13 | 25 | 145 |
| 14 | 23 | 120 |
| 15 | 22 | 110 |
| 16 | 24 | 130 |
| 17 | 25 | 145 |
| 18 | 26 | 155 |
| 19 | 27 | 165 |
| 20 | 28 | 175 |
| 21 | 29 | 185 |
| 22 | 30 | 195 |
| 23 | 28 | 170 |
| 24 | 27 | 160 |
| 25 | 26 | 150 |
| 26 | 25 | 140 |
| 27 | 24 | 130 |
| 28 | 23 | 120 |
| 29 | 22 | 110 |
| 30 | 21 | 100 |
计算过程
-
计算均值:
- 温度均值 ( T ˉ \bar{T} Tˉ) = 20 + 22 + 25 + … + 21 30 \frac{20 + 22 + 25 + \ldots + 21}{30} 3020+22+25+…+21 ≈ 25.4
- 销量均值 ( V ˉ \bar{V} Vˉ) = 100 + 120 + 140 + … + 100 30 \frac{100 + 120 + 140 + \ldots + 100}{30} 30100+120+140+…+100 ≈ 146.33
-
计算协方差:
- 使用协方差公式: Cov ( T , V ) = 1 n ∑ i = 1 n ( t i − T ˉ ) ( v i − V ˉ ) \text{Cov}(T, V) = \frac{1}{n} \sum_{i=1}^{n} (t_i - \bar{T})(v_i - \bar{V}) Cov(T,V)=n1∑i=1n(ti−Tˉ)(vi−Vˉ)
-
实际计算:
-
以第一组数据为例:
- 温度偏差 d T ( 1 ) = 20 − 25.4 = − 5.4 d_T(1) = 20 - 25.4 = -5.4 dT(1)=20−25.4=−5.4
- 销量偏差 d V ( 1 ) = 100 − 146.33 = − 46.33 d_V(1) = 100 - 146.33 = -46.33 dV(1)=100−146.33=−46.33
- 乘积 p 1 = ( − 5.4 ) × ( − 46.33 ) = 250.182 p_1 = (-5.4) \times (-46.33) = 250.182 p1=(−5.4)×(−46.33)=250.182
-
重复此过程,计算所有数据点的乘积并求和,然后除以数据点的数量 n n n。
-
-
结果:
- 经过计算,我们得到温度和销量之间的协方差大约为 70.48。
结果解释
- 方向:由于协方差为正(70.48),这意味着温度和冰淇淋销量之间存在正向的线性关系。也就是说,随着温度的升高,冰淇淋销量也会增加。
- 强度:仅凭协方差的值 70.48,我们不能直接判断这种关系的强度。为了更好地理解这种关系的强度,我们可以计算皮尔逊相关系数,它是协方差除以两个变量标准差的乘积。
计算相关系数
为了计算相关系数,我们需要知道温度和销量的标准差。假设我们已经计算出温度的标准差为 2.67,销量的标准差为 26.55。
- 相关系数:
r = Cov ( T , V ) σ T ⋅ σ V = 70.48 2.67 × 26.55 ≈ 0.994 r = \frac{\text{Cov}(T, V)}{\sigma_T \cdot \sigma_V} = \frac{70.48}{2.67 \times 26.55} \approx 0.994 r=σT⋅σVCov(T,V)=2.67×26.5570.48≈0.994
这里我们得到了一个接近1的值,这意味着温度和销量之间存在非常强的正相关关系。其中, σ T \sigma_T σT和 σ V \sigma_V σV分别表示 T T T和 V V V的标准差。
为什么使用协方差?
尽管协方差可以提供关于两个变量之间线性关系方向的信息,但它有几个局限性:
- 尺度依赖性:协方差的值受到变量尺度的影响,这意味着变量单位的不同会导致协方差值的差异。
- 缺乏标准化:协方差值本身并不能直接告诉我们变量之间线性关系的强度。
替代概念:
- 皮尔逊相关系数:这是一个标准化的度量,消除了变量尺度的影响,并且取值范围为 [ − 1 , 1 ] [-1, 1] [−1,1]。它可以更直观地反映变量之间的线性关系强度。
- 斯皮尔曼等级相关系数:适用于非线性关系的度量,特别是在变量不是正态分布的情况下。
- 肯德尔等级相关系数:类似于斯皮尔曼等级相关系数,但更适用于小样本情况。
何时使用协方差:
- 初步分析:在进行初步的数据探索时,协方差可以快速提供变量间关系的方向信息。
- 联合分布:协方差矩阵在多元统计分析中非常有用,特别是在主成分分析、因子分析等高级统计方法中。
为什么选择协方差:
- 简单易用:协方差的计算相对简单,不需要复杂的数学知识。
- 基础统计量:协方差是许多高级统计方法的基础,例如主成分分析等。
结论
通过分析,我们可以得出结论:
- 当温度升高时,冰淇淋销量也会显著增加。这表明在炎热的日子里,顾客更倾向于购买冰淇淋。
- 这种正相关关系非常强,相关系数接近 1,表明温度是影响冰淇淋销量的关键因素之一。
商业启示
基于这些发现,你可以采取相应的措施来优化业务运营,比如:
- 在预测到气温较高的日子时,提前准备更多的冰淇淋库存。
- 根据温度变化调整营销策略和促销活动。
相关文章:

协方差详解及在日常生活中的应用实例——天气温度与冰淇淋销量的关系
协方差详解及在日常生活中的应用实例——天气温度与冰淇淋销量的关系 文章目录 协方差详解及在日常生活中的应用实例——天气温度与冰淇淋销量的关系引言协方差的概念与背景数学公式推导实例背景数据收集计算过程结果解释计算相关系数为什么使用协方差?结论商业启示…...
Spring Boot3.3.X整合Mybatis-Plus
前提说明: 项目的springboot版本为:<version>3.3.2</version> 需要整合的mybatis-plus版本:<version>3.5.7</version> 废话不多说,开始造吧 1.准备好数据库和表 2.配置全局文件application.properti…...
快速了解软件测试——测试用例的方法
测试用例的编写方法有八种,其中等价类、边界值、判定表、场景法、流程图重要且使用得多 ●等价类●边界值●判定表●因果图[了解]●正交法[了解]●场景法●流程图●错误推测法[了解] 1、等价类 为什么要用等价类划分法? ●从大量数据中划分范围(等价类),然后从每…...
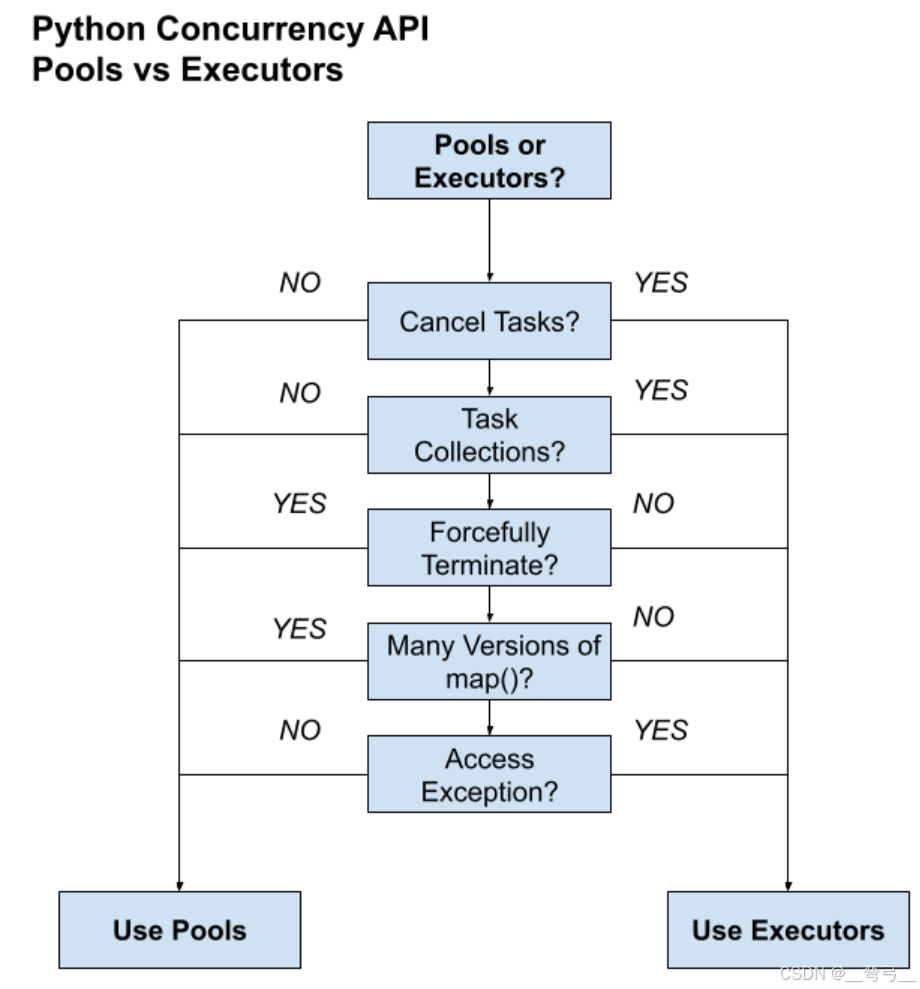
多线程、多进程,还是异步?-- Python 并发 API 如何选择
如何选择正确的 Python 并发 API模块 ? Python 标准库提供了三种并发 API , 如何知道你的项目应该使用哪个 API? 在本教程将带逐步了解各API的特性、区别以及各自应用场景,指导你选择最合适的并发 API。 多线程、多进程࿰…...
汽车服务管理系统 _od8kr
TOC springboot580汽车服务管理系统 _od8kr--论文 系统概述 该系统由个人管理员和员工管理,用户三部分组成。其中:用户进入系统首页可以实现首页,热销汽车,汽车配件,汽车资讯,后台管理,在线客…...
带你玩转小程序推广,实现短链接一键跳转
不知道各位有没有想过,短链接直接跳转到微信小程序到底该怎么操作呢?掌握这个小技能,能让你的推广效率大幅提升哦。今天就给大家分享一个全新方法,教你如何从短链接直接跳转到微信小程序,实现高效的一键式跨越。 一、…...
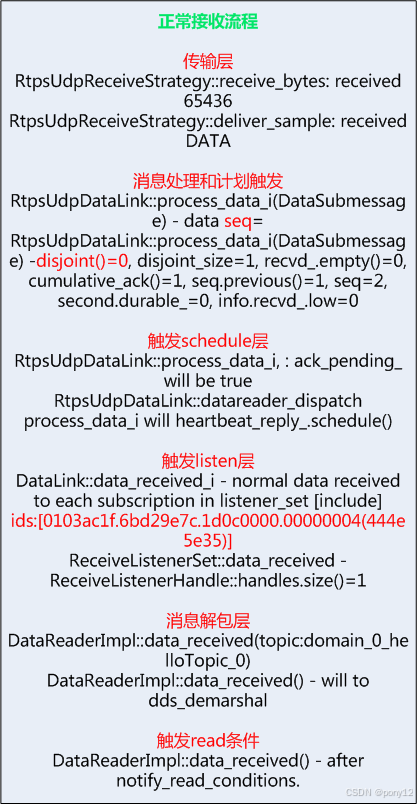
OpenDDS的Rtps_Udp传输协议可靠性QoS收发基本流程
OpenDDS中,实现了Rtps_Udp传输协议(非纯udp)的可靠性传输。传输的线程包括: 1)发送方线程主要线程和定时器 《1》应用线程 《2》网络异步发送线程 《3》Heartbeat定时器 《4》Nak_response定时器 2)接收方主要线程和定时器 《1》网络异步接收线程 《2》heartbeat_respons…...

体育数据API纳米奥运会数据API:高阶数据包接口文档API示例⑦
纳米体育数据的数据接口通过JSON拉流方式获取200多个国家的体育赛事实时数据或历史数据的编程接口,无请求次数限制,可按需购买,接口稳定高效;覆盖项目包括足球、篮球、网球、电子竞技、奥运等专题、数据内容。 纳米数据API2.0版本…...

【中项第三版】系统集成项目管理工程师 | 第 15 章 组织保障
前言 本章的知识点预计上午会考1-2分,下午可能会考,一般与其他管理领域进行结合考查。学习要以教材为主。 目录 15.1 信息和文档管理 15.1.1 信息和文档 15.1.2 信息(文档)管理规则和方法 15.2 配置管理 15.2.1 基本概念 …...
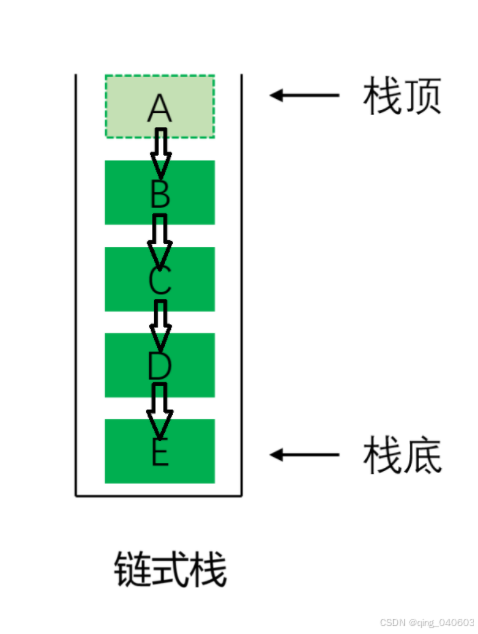
数据结构——顺序栈和链式栈
目录 引言 栈的定义 栈的分类 栈的功能 栈的声明 1.顺序栈 2.链式栈 栈的功能实现 1.栈的初始化 (1)顺序栈 (2)链式栈 (3)复杂度分析 2.判断栈是否为空 (1)顺序栈 (2)链式栈 (3)复杂度分析 3.返回栈顶元素 (1)顺序栈 (2)链式栈 (3)复杂度分析 4.返回栈的大…...

PHP轻创推客集淘客地推任务平台于一体的综合营销平台系统源码
🚀轻创推客,营销新纪元 —— 集淘客与地推任务于一体的全能平台🌐 🌈【开篇:营销新潮流,轻创推客引领未来】 在瞬息万变的营销世界里,你还在为寻找高效、全面的营销渠道而烦恼吗?&…...

three.js实现 加载3dtiles ,瓦片 ,倾斜摄影,功能
预览:https://z2586300277.github.io/three-cesium-examples/#/codeMirror?navigationThreeJS&classifyexpand&idloadTiles 部署站点预览:http://threehub.cn/ 开源地址:https://z2586300277.github.io/three-cesium-examples/#/e…...

Qt QTextEdit调用append数据重复的问题
使用QTextEdit写了个串口工具, 当串口有数据时通过一个signal传给slot,在 slot中调用QTextEdit的append(text)来增量显示串口数据,当串口关闭时调用clear()来清空显示。 结果发现append调用后显示的数据会有重复。 分析 分析代码࿰…...

数学基础(二)
一、导数 导数计算: 偏导数: 方向导数: 梯度: 函数在某点的梯度是一个向量,它的方向余方向导数最大值取得的方向一致。其大小正好是最大的方向导数 二、微积分 面积由来: 切线: 定积分&#x…...

Java设计模式原则及中介者模式研究
在软件开发过程中,设计模式作为解决常见设计问题的有效工具,对于提升代码质量、促进团队协作具有重要意义。本文系统地阐述了Java设计模式的六大基本原则——单一职责原则、开放封闭原则、里氏替换原则、依赖倒置原则、接口隔离原则以及迪米特法则&#…...

logstash入门学习
1、入门示例 1.1、安装 Redhat 平台 rpm --import http://packages.elasticsearch.org/GPG-KEY-elasticsearch cat > /etc/yum.repos.d/logstash.repo <<EOF [logstash-5.0] namelogstash repository for 5.0.x packages baseurlhttp://packages.elasticsearch.org…...

【代码】Swan-Transformer 代码详解(待完成)
1. 局部注意力 Window Attention (W-MSA Module) class WindowAttention(nn.Module):r""" Window based multi-head self attention (W-MSA) module with relative position bias.It supports both of shifted and non-shifted window.Args:dim (int): Number…...

iframe.contentDocument 和document.documentElement的区别
iframe.contentDocument 和 document.documentElement 是用于访问不同内容的两个不同的对象或属性。 1. iframe.contentDocument 内容: iframe.contentDocument 代表的是 <iframe> 元素所嵌入的文档的 Document 对象。它允许你访问和操作嵌入的文档(即 ifram…...
)
计算机操作员试题(中篇)
计算机操作员试题(中篇) 335.在 Excel中,把鼠标指向被选中单元格边框,当指变成箭头时,拖动鼠标到目标单 元格时,将完成( )操作。 (A)删除 (B)移动 ©自动填充 (D)复制 336.在 Excel 工作表的单元格中,如想输入数字字符串 070615 (例如学号),则应输 入()。 (A) 0007…...
车规级MCU「换道」竞赛
汽车芯片,尤其是MCU市场正在进入拐点期。 本周,总部位于荷兰的汽车芯片制造商—恩智浦(NXP)半导体总裁兼首席执行官Kurt Sievers在公司第二季度财报电话会议上告诉投资者,由于汽车需求停滞不前,该公司正在努…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

【Pandas】pandas DataFrame dropna
Pandas2.2 DataFrame Missing data handling 方法描述DataFrame.fillna([value, method, axis, …])用于填充 DataFrame 中的缺失值(NaN)DataFrame.backfill(*[, axis, inplace, …])用于**使用后向填充(即“下一个有效观测值”)…...

mq安装新版-3.13.7的安装
一、下载包,上传到服务器 https://github.com/rabbitmq/rabbitmq-server/releases/download/v3.13.7/rabbitmq-server-generic-unix-3.13.7.tar.xz 二、 erlang直接安装 rpm -ivh erlang-26.2.4-1.el8.x86_64.rpm不需要配置环境变量,直接就安装了。 erl…...

华硕电脑,全新的超频方式,无需进入BIOS
想要追求更佳性能释放 或探索更多可玩性的小伙伴, 可能会需要为你的电脑超频。 但我们常用的不论是BIOS里的超频, 还是Armoury Crate奥创智控中心超频, 每次调节都要重启,有点麻烦。 TurboV Core 全新的超频方案来了 4不规…...
