【数据结构】详解二叉树与堆与堆排序的关系
🌇个人主页:平凡的小苏
📚学习格言:别人可以拷贝我的模式,但不能拷贝我不断往前的激情
🛸C语言专栏:https://blog.csdn.net/vhhhbb/category_12174730.html
🚀数据结构专栏:https://blog.csdn.net/vhhhbb/category_12211053.html
家人们更新不易,你们的👍点赞👍和⭐关注⭐真的对我真重要,各位路过的友友麻烦多多点赞关注,欢迎你们的私信提问,感谢你们的转发!
关注我,关注我,关注我,你们将会看到更多的优质内容!!


目录
1、树概念及结构
1.1、树的概念
1.2 树的相关概念
2、二叉树概念及结构
2.1、概念
2.2、 特殊的二叉树
2.3、二叉树的性质
2.5 、二叉树的存储结构
3、二叉树的顺序结构及实现
3.1、 二叉树的顺序结构
3.2、堆的概念及结构
3.3、堆的实现
3.3.1、堆的结构代码
3.3.2、堆的初始化
3.3.3、堆的插入
3.3.4、堆的删除
3.3.5、取堆顶数据
3.3.6、堆的个数
3.3.7、堆的判空
3.3.8、堆的销毁
3.4、建堆的时间复杂度
3.4.1、向上建堆的时间复杂度
3.4.2、向下调整建堆的时间复杂度证明
3.5、堆的应用
3.5.1、堆排序
3.5.2、堆排序代码
3.5.3、TOP-K问题
1、树概念及结构
1.1、树的概念
- 有一个特殊的结点,称为根结点,根节点没有前驱结点
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 因此,树是递归定义的。
下面我们来看一个树的结构图:

注意:树形结构中,子树之间是不能有交集的,否则就不是树形结构,变成了一个图。
1.2 树的相关概念

2、二叉树概念及结构
2.1、概念

从上图可以看出:
2.2、 特殊的二叉树

2.3、二叉树的性质
2.5 、二叉树的存储结构
目前我们是需要讲堆结构的,这里只详细介绍二叉树的顺序存储

3、二叉树的顺序结构及实现
3.1、 二叉树的顺序结构
3.2、堆的概念及结构
堆是具有下列性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆(例如下面第一张图所示);或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆(例如下面第二张图所示)


3.3、堆的实现
3.3.1、堆的结构代码
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;//数组int size;//堆结点个数int capacity;//堆的容量
}Heap;3.3.2、堆的初始化
// 堆的构建
void HeapCreate(Heap* hp)
{assert(hp);hp->a = (HPDataType*)malloc(sizeof(int) * 4);hp->size = 0;hp->capacity = 4;
}3.3.3、堆的插入
//堆的向上调整
void AdjustUp(HPDataType* a, int child)
{//这里构建的是大根堆int parent = (child - 1) / 2;while (child > 0)//如果孩子结点不大于0就跳出循环{if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;//孩子结点走到父节点parent = (child - 1) / 2;//更新父节点}else{break;}}
}
void HeapPush(Heap* hp, HPDataType x)
{assert(hp);if (hp->size == hp->capacity)//判断堆的容量是否满足{HPDataType* tmp = (HPDataType*)realloc(hp->a, sizeof(int) * hp->capacity * 2);if (tmp == NULL){perror("realloc fail:");exit(-1);}hp->a = tmp;hp->capacity *= 2;}hp->a[hp->size] = x;hp->size++;AdjustUp(hp->a, hp->size - 1);//插入向上调整算法
}算法思想:
我们每次向堆里面插入一个树,都需要调用向上调整算法,如果我们不这样操作,那么我们插入的数就不是一个大根堆,就无法实现堆的删除,取前k大的数等等操作
1.首先我们先让插入的数当做孩子结点,拿去和父亲结点比较,如果孩子结点大于父结点,那么我们就需要交换
2.更新孩子结点和父节点
3.孩子结点不大于0就跳出循环
3.3.4、堆的删除
//堆的向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{int child = 2 * parent + 1;while (child < n){if (child + 1 < n && a[child + 1] > a[child]){child += 1;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = 2 * parent + 1;}else{break;}}
}
void HeapPop(Heap* hp)
{assert(hp);Swap(&hp->a[0], &hp->a[hp->size - 1]);将堆顶的数和最后一个叶子结点交换hp->size--;//堆个数减1AdjustDown(hp->a, hp->size, 0);//调用向下调整算法
}算法思想:
1.交换堆顶和最后叶子结点
2.堆个数减12,并且调用向下调整算法
3.找到孩子两个孩子结点中最小的结点,将™交换
4.更新父节点和孩子结点
5.如果孩子结点大于结点个数就退出循环
3.3.5、取堆顶数据
HPDataType HeapTop(Heap* hp)
{assert(hp);return hp->a[0];
}3.3.6、堆的个数
int HeapSize(Heap* hp)
{assert(hp);return hp->size;
}3.3.7、堆的判空
bool HeapEmpty(Heap* hp)
{assert(hp);return hp->size == 0;
}3.3.8、堆的销毁
void HeapDestory(Heap* hp)
{assert(hp);free(hp->a);hp->capacity = hp->size = 0;
}3.4、建堆的时间复杂度
3.4.1、向上建堆的时间复杂度

时间复杂度证明如下图所示:
3.4.2、向下调整建堆的时间复杂度证明
向下调整建堆的时间复杂度是O(N),是向上调整建堆的时间复杂度的优化
计算证明如下图所示:

3.5、堆的应用
3.5.1、堆排序
堆排序就是利用堆进行排序的方法。它的基本思想是,将待排序的序列构造成一个大顶堆。此时,整个序列的最大值就是堆顶的根节点。将它移走(其实就是将其与堆数组的末尾元素交换,此时末尾元素就是最大值),然后将剩余的n-1个序列重新构造一个堆,这就会得到n个元素的次大值。如此反复执行,便能得到一个有序序列。
注意:我们需要升序,就需要建大堆。降序就需要建小堆。
堆排序的图形演示:
从左至右,从上至下演示


3.5.2、堆排序代码
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
void Swap(int* p1, int* p2)
{int x = *p1;*p1 = *p2;*p2 = x;
}
void PrintArray(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}
}void AdjustDown(int* a, int n, int parent)
{int child = 2 * parent + 1;while (child <= n){if (child + 1 <= n && a[child + 1] < a[child]){child += 1;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = 2 * parent + 1;}else{break;}}
}
void HeapSort(int* a, int n)
{for (int i = (n - 2) / 2; i >= 0; i--){AdjustDown(a, n - 1, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);end--;AdjustDown(a, end, 0);}PrintArray(a, n);
}
int main()
{int a[10] = { 4,2,7,8,3,1,5,6,9,0 };HeapSort(a, sizeof(a) / sizeof(a[0]));return 0;
}3.5.3、TOP-K问题
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<time.h>
void Swap(int * p1,int * p2)
{int x = *p1;*p1 = *p2;*p2 = x;
}
//堆的向下调整
void AdjustDown(int * a, int n, int parent)
{int child = 2 * parent + 1;while (child < n){if (child + 1 < n && a[child + 1] < a[child]){child += 1;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = 2 * parent + 1;}else{break;}}
}
void PrintTopK(const char* fin, int k)
{// 1. 建堆--用a中前k个元素建堆int* topK = (int*)malloc(sizeof(int) * k);if (topK == NULL){perror("malloc fail:");return;}FILE* fout = fopen(fin, "r");if (fout == NULL){perror("FILE fail");return;}for (int i = 0; i < k; i++){fscanf(fout,"%d",&topK[i]);}// 2. 将剩余n-k个元素依次与堆顶元素交换,不满则则替换for (int i = (k - 2) / 2; i >= 0; i--){AdjustDown(topK, k, i);}int val = 0;int ret = fscanf(fout, "%d", &val);while (ret != EOF){if (val > topK[0]){topK[0] = val;AdjustDown(topK, k, 0);}ret = fscanf(fout, "%d", &val);}for (int i = 0; i < k; i++){printf("%d ", topK[i]);}printf("\n");free(topK);fclose(fout);
}void CreateNDate()
{// 造数据int n = 10000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (size_t i = 0; i < n; ++i){int x = rand() % 10000;fprintf(fin, "%d\n", x);}fclose(fin);
}int main()
{CreateNDate();PrintTopK("data.txt", 10);return 0;
}
注:这里得到的就是前10个最大的数
好了!小编的分享到这里就结束了,有什么不足的地方请大佬多多指教!!!
相关文章:

【数据结构】详解二叉树与堆与堆排序的关系
🌇个人主页:平凡的小苏 📚学习格言:别人可以拷贝我的模式,但不能拷贝我不断往前的激情 🛸C语言专栏:https://blog.csdn.net/vhhhbb/category_12174730.html 🚀数据结构专栏ÿ…...
【Pandas】数据分析入门
文章目录前言一、Pandas简介1.1 什么是Pandas1.2 Pandas应用二、Series结构2.1 Series简介2.2 基本使用三、DataFrame结构3.1 DataFrame简介3.2 基本使用四、Pandas-CSV4.1 CSV简介4.2 读取CSV文件4.3 数据处理五、数据清洗5.1 数据清洗的方法5.2 清洗案例总结前言 大家好&…...
【c++】:list模拟实现“任意位置插入删除我最强ƪ(˘⌣˘)ʃ“
文章目录 前言一.list的基本功能的使用二.list的模拟实现总结前言 1. list是可以在常数范围内在任意位置进行插入和删除的序列式容器,并且该容器可以前后双向迭代。2. list的底层是双向链表结构,双向链表中每个元素存储在互不相关的独立节点中࿰…...

QT表格控件实例(Table Widget 、Table View)
欢迎小伙伴的点评✨✨,相互学习🚀🚀🚀 博主🧑🧑 本着开源的精神交流Qt开发的经验、将持续更新续章,为社区贡献博主自身的开源精神👩🚀 文章目录前言一、图示实例二、列…...

第二章Vue组件化编程
文章目录模块与组件、模块化与组件化模块组件模块化组件化Vue中的组件含义非单文件组件基本使用组件注意事项使用 kebab-case使用 PascalCase组件的嵌套模板templateVueComponent一个重要的内置功能单文件组件Vue脚手架使用Vue CLI脚手架先配置环境初始化脚手架分析脚手架结构实…...
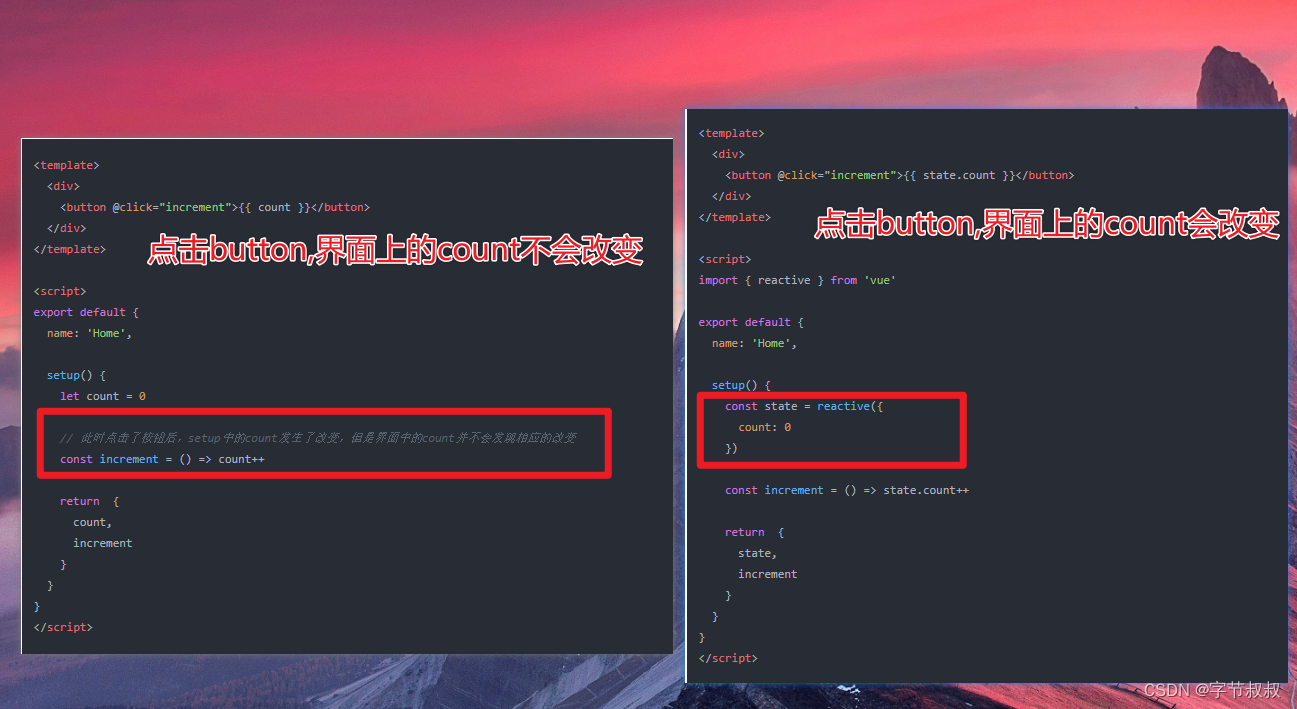
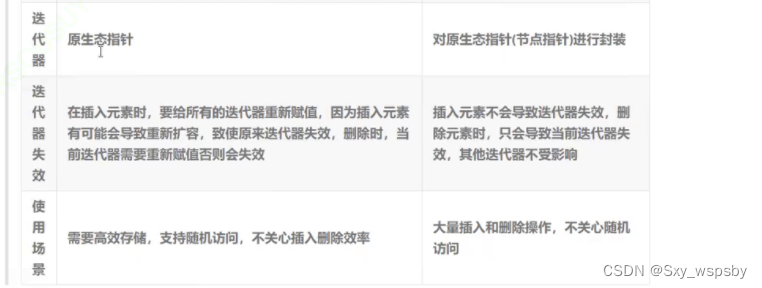
面试官:vue2和vue3的区别有哪些
目录 多根节点,fragment(碎片) Composition API reactive 函数是用来创建响应式对象 Ref toRef toRefs 去除了管道 v-model的prop 和 event 默认名称会更改 vue2写法 Vue 3写法 vue3组件需要使用v-model时的写法 其他语法 1. 创…...

【TopK问题】——用堆实现
文章目录一、TopK问题是什么二、解决方法三、时间复杂度一、TopK问题是什么 TopK问题就是从1000个数中找出前K个最大的数或者最小的数这样的类似问题。 不过并不要求这k个数字必须是有序的,如果题目有要求,则进行堆排序即可。 还有比如求出全国玩韩信…...

【Spring从成神到升仙系列 四】从源码分析 Spring 事务的来龙去脉
👏作者简介:大家好,我是爱敲代码的小黄,独角兽企业的Java开发工程师,CSDN博客专家,阿里云专家博主📕系列专栏:Java设计模式、数据结构和算法、Kafka从入门到成神、Kafka从成神到升仙…...

使用Nginx反向代理OpenAI API
由于OpenAI的API在国内无法访问,所以可以通过海外服务器利用Nginx实现反向代理。 安装Nginx 这一步就不赘述了,不同的Linux系统安装方式略有不同,根据自己的服务器的系统自行百度即可。 OpenSSL创建证书 因为OpenAI的接口是https协议的&a…...
)
USB键盘实现——字符串描述符(四)
字符串描述符 字符串描述符内容解析和 HID鼠标 一致。 获取字符串描述符请求 标准设备请求 typedef struct __attribute__ ((packed)){union {struct __attribute__ ((packed)) {uint8_t recipient : 5; ///< Recipient type usb_request_recipient_t.uint8_t type …...
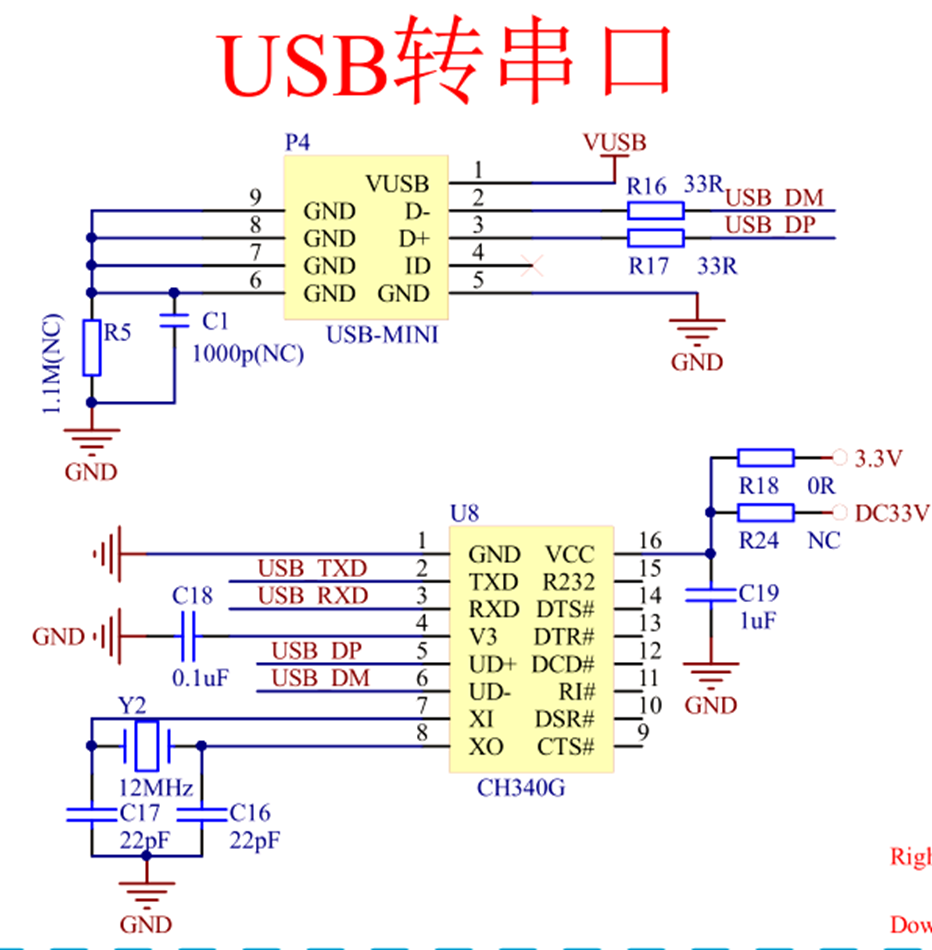
STM32的中断
目录 一、STM32中断概述 二、外部中断控制器EXTI 三、按键中断 四、串口中断 一、STM32中断概述 处理器中的中断在处理器中,中断是一个过程,即CPU在正常执行程序的过程中,遇到外部/内部的紧急事件需要处理,暂时中止当前程序的…...
Flink进阶篇-CDC 原理、实践和优化采集到Doris中
简介 基于doris官方用doris构建实时仓库的思路,从flinkcdc到doris实时数仓的实践。 原文 Apache Flink X Apache Doris 构建极速易用的实时数仓架构 (qq.com) 前提-Flink CDC 原理、实践和优化 CDC 是什么 CDC 是变更数据捕获(Change Data Captur…...

看完这篇 教你玩转渗透测试靶机vulnhub——My File Server: 1
Vulnhub靶机My File Server: 1渗透测试详解Vulnhub靶机介绍:Vulnhub靶机下载:Vulnhub靶机安装:Vulnhub靶机漏洞详解:①:信息收集:②:FTP匿名登入:③:SMB共享服务…...

OpenHarmony实战STM32MP157开发板 “控制” Hi3861开发板 -- 中篇
一、前言 我们在 OpenHarmony实战STM32MP157开发板 “控制” Hi3861开发板 – 上篇 中介绍到了,App面板的开发,以及JS API接口的开发和调用。 那么本篇文章,会详解:BearPi-HM Nano开发板,如何实现数据上报和指令接收响应的。 看到这里,可能有同学可能已经知道思路了,因…...
【数据结构初阶】单链表
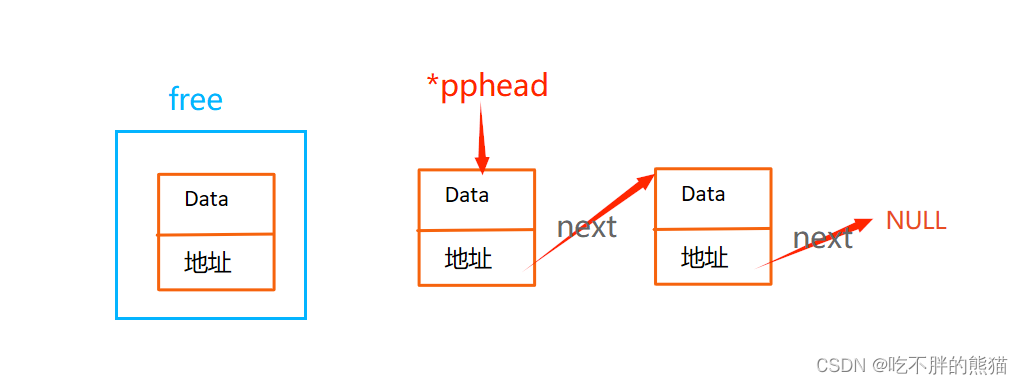
目录一、思路>>>>>>>>>>>>过程<<<<<<<<<<<<<<<1.打印2.尾插3.尾删4.头插5.头删6.查找7.指定位置后插入8.指定位置后删除9.链表的销毁二、整个程序1.SLTlist.c2.SLTlist.c一、思路 #define …...

多线程代码案例-阻塞队列
hi,大家好,今天为大家带来多线程案例--阻塞队列 这块知识点也很重要,要好好掌握呀~~~ 🌸🌸🌸🌸🌸🌸🌸🌸🌸🌸🌸🌸🌸&#x…...
mysql的limit查询竟然有坑?
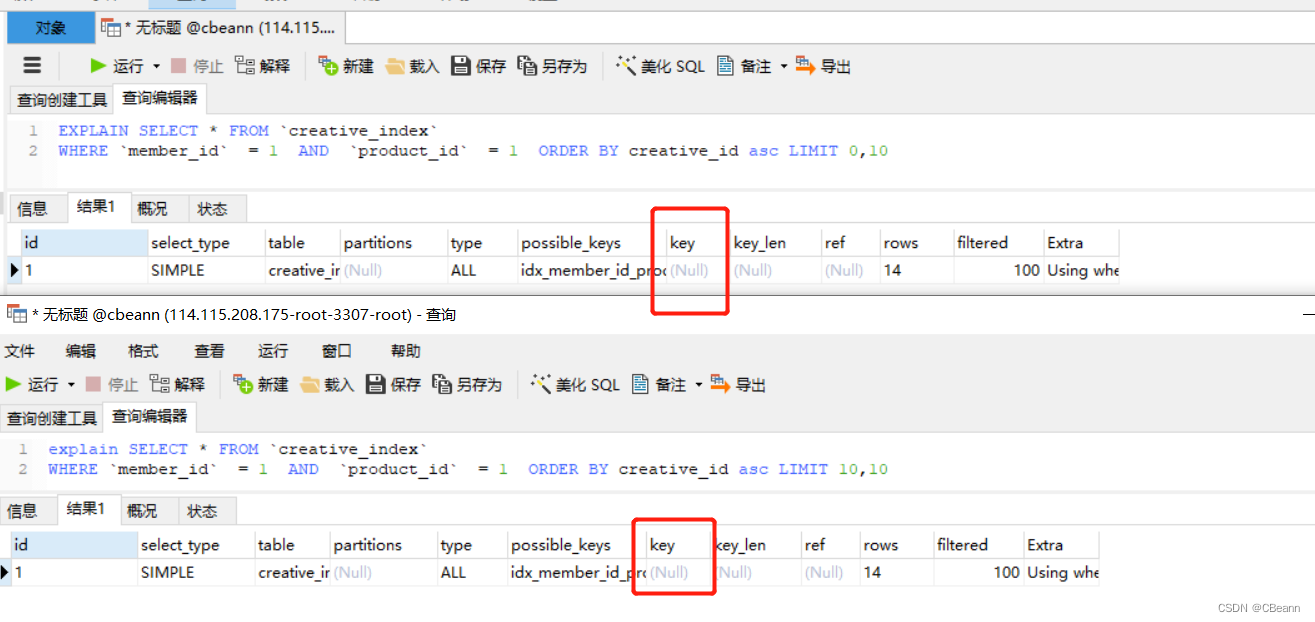
背景 最近项目联调的时候发现了分页查询的一个bug,分页查询总有数据查不出来或者重复查出。 数据库一共14条记录。 如果按照一页10条。那么第一页和第二页的查询SQL和和结果如下。 .png) 那么问题来了,查询第一页和第二页的时候都出现了11,12,13的记录…...
【Docker】MAC电脑下的Docker操作
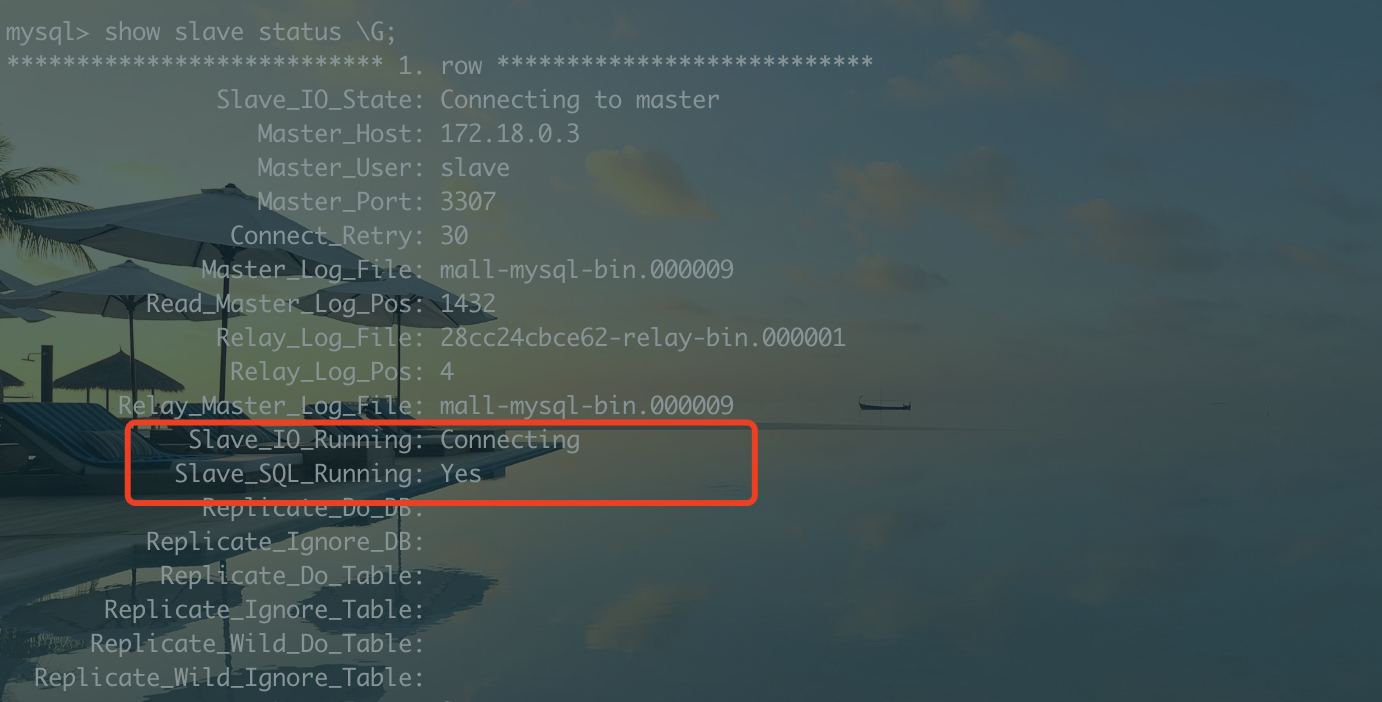
文章目录安装Docker部署mysql 一主一从登录ChatGPT搞方案本地创建一个文件夹编辑docker-compose.yml文件启动检查并编排容器验证基于command的my.cnf配置的加载主数据库建一个用户给子数据库用于主从复制启动主从同步安装Docker 官网地址 https://www.docker.com/ 下载安装 验…...

【Python3】matplotlib,模块,进/线程,文件/xml,百度人脸api,hal/aiohttp/curl
文章目录1.matplotlib/时间复杂度/线性表:顺序表要求存储空间必须连续2.python模块导入:python3 -c ‘import sys;print(sys.path)’ 显示导入模块时会去哪些路径下查找3.进/线程:进/线程是不能随便创建,就像每招一个员工是有代价…...
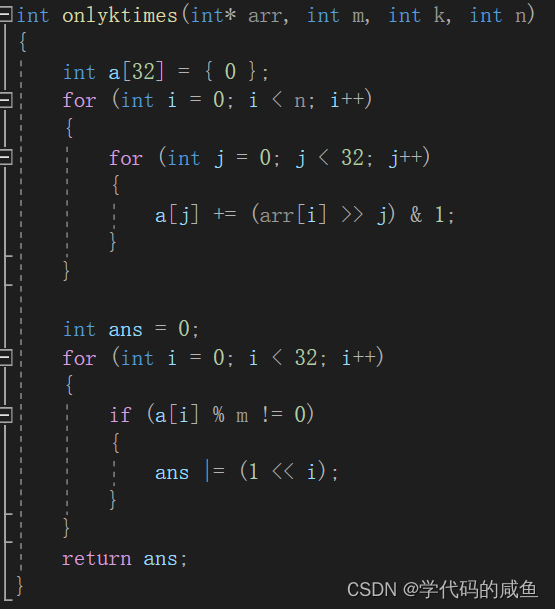
异或相关算法
文章目录1. 异或的性质2. 题目一3. 题目二4. 题目三5. 题目四1. 异或的性质 我们知道,异或的定义是:相同为0,相异为1。所以也被称为无进位相加,根据这定义,我们可以得出三个性质: 1. N ^ N0。2. N ^ 0N。3…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
