【蓝桥杯专题】 树状数组(C++ | 洛谷 | acwing | 蓝桥)
菜狗现在才开始备战蓝桥杯QAQ
文章目录
- 【蓝桥杯专题】 (C++ | 洛谷 | acwing | 蓝桥)
- 什么是线段数组??
- 1264. 动态求连续区间和
- 数星星
- 线段树
- AcWing 1270. 数列区间最大值
- P
- P
- P
- P
- P
- P
- P

【蓝桥杯专题】 (C++ | 洛谷 | acwing | 蓝桥)
什么是线段数组??
OI wiki
- 树状数组是一种支持 单点修改 和 区间查询 的,代码量小的数据结构。
- 俩个操作的时间复杂度均为
O(logn)

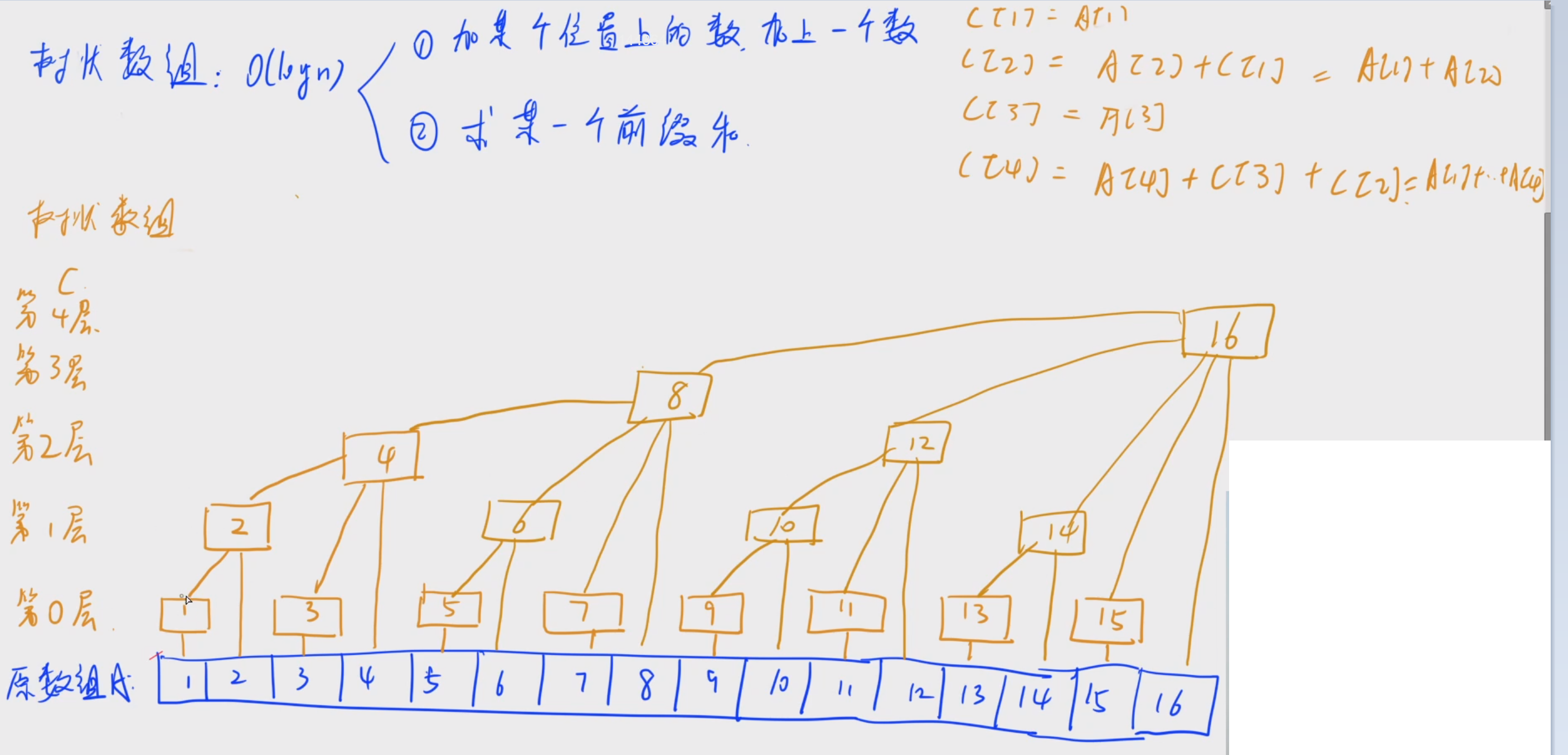
- lowbit()函数
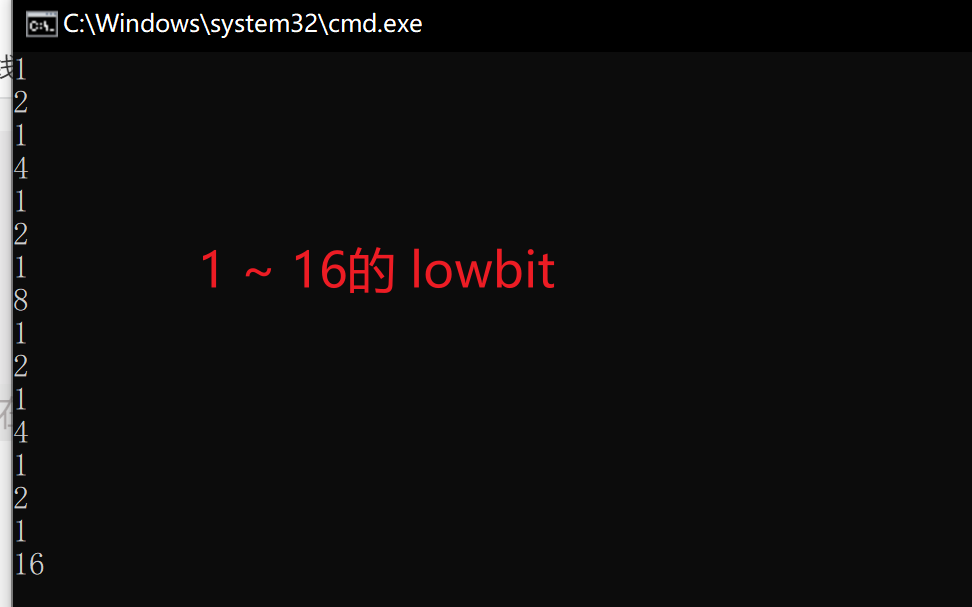
int lowbit(int x) { // 返回二进制中最后一个 1// x 的二进制中,最低位的 1 以及后面所有 0 组成的数。// lowbit(0b01011000) == 0b00001000// ~~~~^~~~// lowbit(0b01110010) == 0b00000010// ~~~~~~^~return x & -x;
}

1264. 动态求连续区间和

链接 链接
#include<bits/stdc++.h>using namespace std;const int N=100009;int a[N],tr[N];int n,m;//每个数的间隔,背下来就行
int lowbit(int x)
{return x&-x;
}//第x个数加上v
int add(int x,int v)
{//因为树状数组的性质,加一个数,只影响logn个数,所有不用全加完//从当前位置开始加,每个间隔是lowbit(i),一直加到最后for(int i=x;i<=n;i+=lowbit(i))tr[i]+=v;
}//返回x的前缀和
int qurry(int x)
{//因为树状数组的性质,求前缀和,只用加logn个数,所有不用全加完//从当前位置开始累加,每个间隔是lowbit(i),一直加到i==0停止int cnt=0;for(int i=x;i!=0;i-=lowbit(i))cnt+=tr[i];return cnt;
}int main()
{cin>>n>>m;for(int i=1;i<=n;i++)scanf("%d",&a[i]);for(int i=1;i<=n;i++)add(i,a[i]);//第i个数加上a[i]while(m--){int k,x,y;scanf("%d%d%d",&k,&x,&y);if(k==0) printf("%d\n",qurry(y)-qurry(x-1));else add(x,y);}return 0;}数星星
由于本题输入数据很特殊,所以其实等价于求一下,到目前的输入为止,有多少个星星的 x 值小于等于该星星的 x 就可以了,这就代表该星星的等级。
由于该题y不递减的输入特性,导致了y在题目中毫无作用
链接 链接
#include <bits/stdc++.h>
// #include <iostream>
using namespace std;
typedef long long ll;
typedef double db;
#define rep(i, a, n) for(int i = a; i <= n; i ++)
#define per(i, a, n) for(int i = n; i <= a; i --)
#define pb push_back;
#define fs first;
#define sz second;
#include <stdlib.h> // atoi
#define debug cout<<"debug"<<"\n"
#define endl "\n";
const int INF = 0x3f3f3f3f;
const int mod=1e9+7;
const int N = 1e5 + 10;
int n;
int ans[N];
int c[N];int lowbit(int x) {return x & -x;
}void add(int x, int v) {//更新整棵树for(int i = x; i <= 32001; i += lowbit(i)) {c[i] += v;}
}// 计算前缀和
int query(int x) {int res = 0;for(int i = x; i > 0; i -= lowbit(i)) res += c[i];return res;
}void solve () {cin >> n;rep(i, 1, n) {int x, y;cin >> x >> y;x ++;/*为了防止出现0的情况,给它全体横坐标加上 1 就好了。这其实是一个很小的细节,作者但是做的时候没考虑到然后就wa了,而给每个 x 都加上 1 并不会影响结果*/add(x, 1);ans[query(x)] ++; /*然后查一下它的前缀和是多少,前缀和是多少就意味着是多少级这是一个动态变化的过程,而且后面的一定比前面高所以要实时计算*/}for(int i = 1;i <= n; i ++) {printf("%d\n",ans[i]);//输出每一个等级的数量}}int main(void){freopen("in.txt","r",stdin);ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int T = 1;// cin >> T;while(T --) solve();return 0;
}
线段树
链接 链接
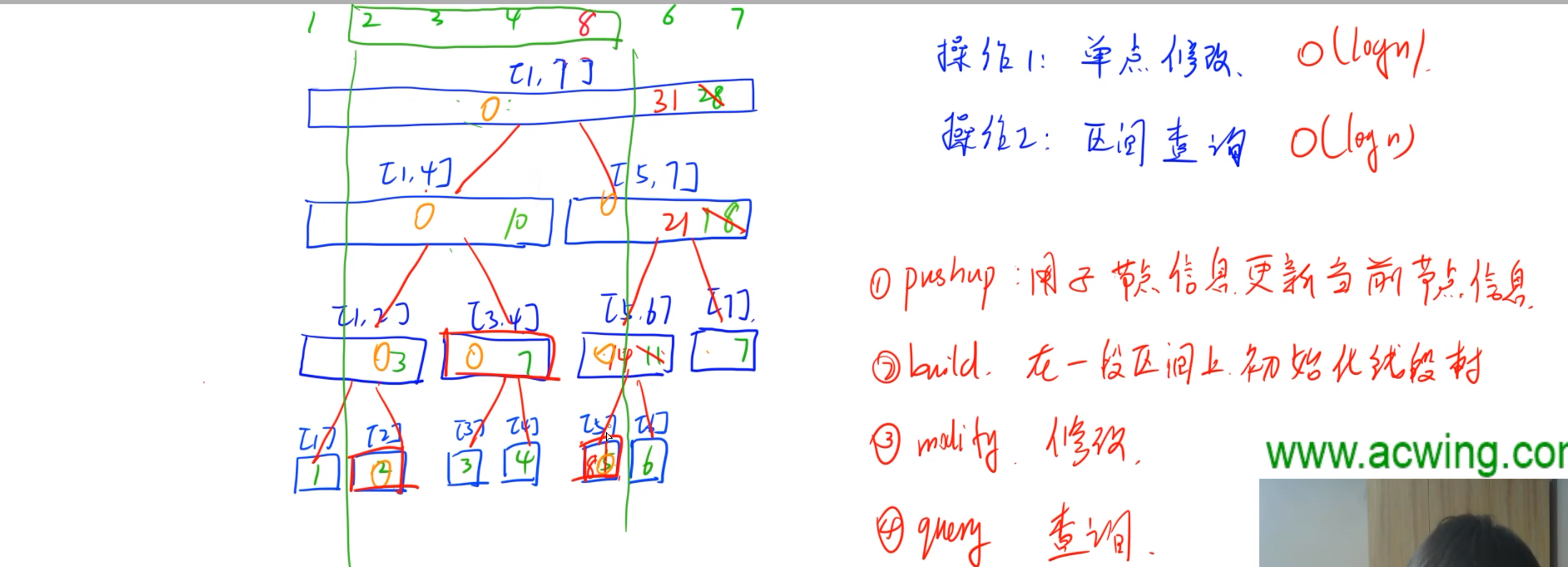
支持:单点修改 区间查询 , 时间复杂度均为log n
//定义节点
struct node{int l,r;//左右区间int sum;//总和
}tr[N*4];//记得开 4 倍空间 (满2叉树 2N - 1 还有空节点 所以为 4N)void push_up(int u) {//利用它的两个儿子来算一下它的当前节点信息 //左儿子 u<<1 ,右儿子 u<<1|1
}void build(int u,int l,int r) {/*第一个参数,当前节点编号,第二个参数,左边界,第三个参数,右边界*///如果当前已经是叶节点了,那我们就直接赋值就可以了//否则的话,说明当前区间长度至少是 2 对吧,那么我们需要把当前区间分为左右两个区间,那先要找边界点//这里记得赋值一下左右边界的初值//边界的话直接去计算一下 l + r 的下取整//先递归一下左儿子//然后递归一下右儿子//做完两个儿子之后的话呢 push_up 一遍u 啊,更新一下当前节点信息}int query(int u,int l,int r)//查询的过程是从根结点开始往下找对应的一个区间
{//如果当前区间已经完全被包含了,那么我们直接返回它的值就可以了//否则的话我们需要去递归来算//计算一下我们 当前 区间的中点是多少//先判断一下和左边有没有交集//用 sum 来表示一下我们的总和//看一下我们当前区间的中点和左边有没有交集//看一下我们当前区间的中点和右边有没有交集}void modify(int u,int x,int v)//第一个参数也就是当前节点的编号,第二个参数是要修改的位置,第三个参数是要修改的值
{//如果当前已经是叶节点了,那我们就直接让他的总和加上 v 就可以了//否则//看一下 x 是在左半边还是在右半边//如果在右半边,那就找右儿子//更新完之后当前节点的信息就要发生变化对吧,那么我们就需要 pushup 一遍
}AcWing 1270. 数列区间最大值
链接 链接
- 思路和线段树类似, sum 改为 maxv
#include <iostream>
#include <cstring>
#include <algorithm>
#include <limits.h>
using namespace std;
const int N = 100010;
int w[N], n, m;struct Segnode {int l, r, maxv; // 把记录区间和的sum换成了记录区间最大值的maxv
}seg[4 * N];void build (int u, int l, int r) {if(l == r) seg[u] = {l, r, w[r]};else {int mid = l + r >> 1;seg[u] = {l , r};build(u * 2, l, mid), build(u * 2 + 1, mid +1 , r);seg[u].maxv = max (seg[u * 2].maxv, seg[u * 2 + 1].maxv);}
}int query(int u, int l, int r) {if(seg[u].l >= l && seg[u].r <= r) return seg[u].maxv ;int res = INT_MIN;int mid = seg[u].l + seg[u].r >> 1;if(r > mid ) res = max(res, query(u * 2 + 1, l , r));if(l <= mid) res = max(res, query(u * 2 , l, r));return res;
}int main()
{int l, r;scanf("%d %d", &n, &m);for (int i = 1; i <= n; ++ i) scanf("%d", &w[i]);build(1, 1, n);while (m --) {scanf("%d %d", &l, &r);printf("%d\n", query(1, l, r));}return 0;
}P
链接 链接
P
链接 链接
P
链接 链接
P
链接 链接
P
链接 链接
P
链接 链接
P
链接 链接

相关文章:

【蓝桥杯专题】 树状数组(C++ | 洛谷 | acwing | 蓝桥)
菜狗现在才开始备战蓝桥杯QAQ 文章目录【蓝桥杯专题】 (C | 洛谷 | acwing | 蓝桥)什么是线段数组??1264. 动态求连续区间和数星星线段树AcWing 1270. 数列区间最大值PPPPPPP【蓝桥杯专题】 (C | 洛谷 | acwing | 蓝桥) 什么是…...

QCefView编译配置(Windows-MSVC)(11)
QCefView编译配置(Windows-MSVC) 文章目录QCefView编译配置(Windows-MSVC)1、概述2、准备工作3、添加环境变量4、更换cef源码版本5、CMake构建6、Visual Studio编译7、安装编译后的文件8、验证编译结果更多精彩内容👉个…...

Token原理
Q:分布式场景下如何生成token以及使用token的流程: 在分布式场景下,可以采用以下方式生成 token 和进行权限认证: 1. 生成 token: 使用JWT(JSON Web Token)生成 token。JWT 是一种基于 JSON …...

③【Java组】蓝桥杯省赛真题 持续更新中...
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ 蓝桥杯真题--持续更新中...一、错误票据题目描…...

linux实验之shell编程基础
这世间,青山灼灼,星光杳杳,秋风渐渐,晚风慢慢 shell编程基础熟悉shell编程的有关机制,如标准流。学习Linux环境变量设置文件及其内容/etc/profile/etc/bashrc/etc/environment~/.profile~/.bashrc熟悉编程有关基础命令…...

C语言小程序:通讯录(静态版)
哈喽各位老铁们,今天给大家带来一期通讯录的静态版本的实现,何为静态版本后面会做解释,话不多说,直接开始!关于通讯录,其实也就是类似于我们手机上的通讯录一样,有着各种各样的功能,…...

写CSDN博客两年半的收获--总结篇
👨💻作者简介:练习时长两年半的java博主 🎟️个人主页:君临๑ ps:点赞是免费的,却可以让写博客的作者开心好几天😎 不知不觉间,在csdn写博客也有两年半的时间了&#x…...
中科亿海微FPGA应用(一、点灯)
1.软件: https://download.csdn.net/download/weixin_41784968/87564071 需要申请license才能使用:软件试用申请_软件试用申请_中科亿海微电子科技(苏州)有限公司 2.开发板: 芯片EQ6HL45,42.5k LUT。 3…...

ElasticSearch - SpringBoot整合ES:实现搜索结果排序 sort
文章目录00. 数据准备01. Elasticsearch 默认的排序方式是什么?02. Elasticsearch 支持哪些排序方式?03. ElasticSearch 如何指定排序方式?04. ElasticSearch 如何按照相关性排序?05. ElasticSearch 查询结果如何不按照相关性排序…...

IDEA的全新UI可以在配置里启用了,快来试试吧!
刚看到IDEA官方昨天发了这样一条推:IDEA的新UI可以在2022.3版本上直接使用了!开启方法如下:打开IDEA的Setting界面,在Appearance & Behavior下有个被标注为Beta标签的New UI菜单,具体如下图:勾选Enable…...

第九章 镜像架构和规划 - 备份处于活动状态时自动进行故障转移
文章目录第九章 镜像架构和规划 - 备份处于活动状态时自动进行故障转移备份处于活动状态时自动进行故障转移备份不活动时的自动故障转移对各种中断场景的镜像响应响应主要中断场景的自动故障转移第九章 镜像架构和规划 - 备份处于活动状态时自动进行故障转移 备份处于活动状态…...

Barra模型因子的构建及应用系列七之Liquidity因子
一、摘要 在前期的Barra模型系列文章中,我们构建了Size因子、Beta因子、Momentum因子、Residual Volatility因子、NonLinear Size因子和Book-to-Price因子,并分别创建了对应的单因子策略,其中Size因子和NonLinear Siz因子具有很强的收益能力…...
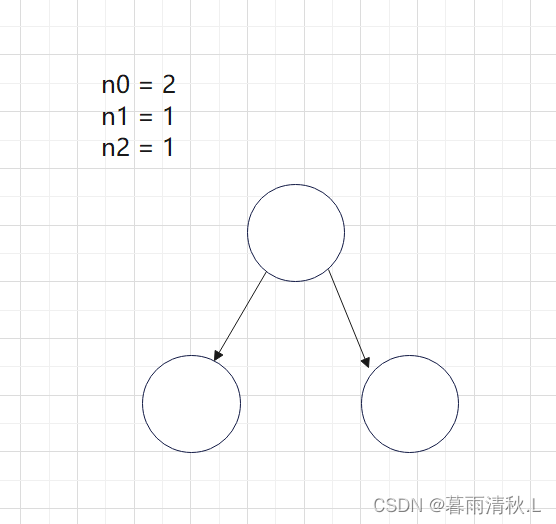
走进二叉树的世界 ———性质讲解
二叉树的性质和证明前言1.二叉树的概念和结构特殊的二叉树:二叉树的性质前言 本篇博客主要讲述的是有关二叉树的一些概念,性质以及部分性质的相关证明,如果大伙发现了啥错误,可以在评论区指出😘😘 1.二叉树…...

【SSM】Spring + SpringMVC +MyBatis 框架整合
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ SSM框架整合一、导入相关依赖二、配置web.xml文…...

【算法基础】一篇文章彻底弄懂Dijkstra算法|多图解+代码详解
博主简介:努力学习的大一在校计算机专业学生,热爱学习和创作。目前在学习和分享:算法、数据结构、Java等相关知识。博主主页: 是瑶瑶子啦所属专栏: 算法 ;该专栏专注于蓝桥杯和ACM等算法竞赛🔥近期目标&…...

第二十三天01MySQL多表查询与事务
目录 1. 多表查询 1.1 概述 1.1.1 数据准备 1.1.2 介绍 1.1.3 分类 1.2 内连接 1.2.1 语法 1.2.2 案例演示 1.3 外连接 1.3.1 语法 1.3.2 案例演示 1.4 子查询 1.4.1 介绍 1.4.2 标量子查询 1.4.3 列子查询 1.4.4 行子查询 1.4.5 表子查询 1.5 案例 1.5.1 介…...
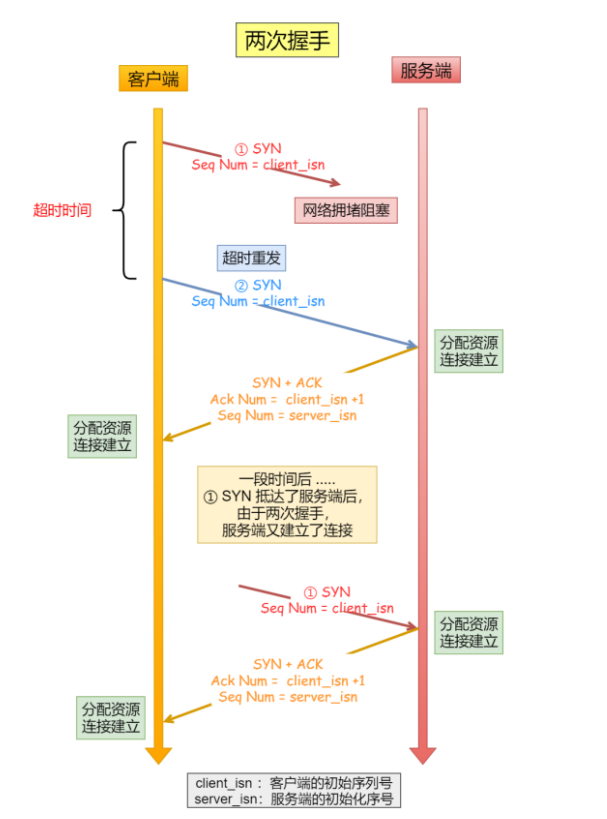
TCP协议详解
1.TCP的准备条件在古代的时候,古人们经常写书信进行交流,写书信的前提是你要知道这份信是要寄给谁在网络中,我们通过ip端口号找对目标对象,但是现在网站一般会对ip端口注册一个域名,所以我们一般就是对域名进行查找&am…...
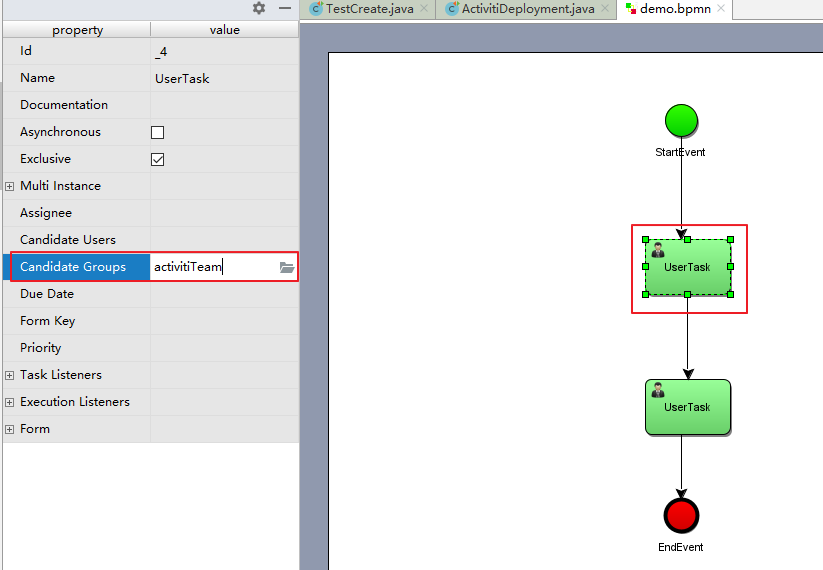
Activiti7与Spring、Spring Boot整合开发
Activiti整合Spring 一、Activiti与Spring整合开发 1.1 Activiti与Spring整合的配置 1)、在pom.xml文件引入坐标 如下 <properties><slf4j.version>1.6.6</slf4j.version><log4j.version>1.2.12</log4j.version> </properties> <d…...
基于SpringBoot实现冬奥会运动会科普平台【源码+论文】
基于SpringBoot实现冬奥会科普平台演示开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包&#…...

一文吃透SpringBoot整合mybatis-plus(保姆式教程)
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

Python异步编程:深入理解协程的原理与实践指南
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 持续学习,不断…...
