(算法基础)朴素版Prim算法
适用情景
在最小生成树问题当中,涉及到权重和最小值。并且这个图是稠密图(n^2 ~ m)的情形下
时间复杂度
O(N^2)
算法解释
先得知道一下什么是无向图的生成树,树总该知道的吧,生成树就是包含这个无向图中的n个点,并且有n-1条边,其实说白了就是一棵树,当于从原先的无向图的结构当中“拿取”一部分组成了一棵树,这棵树就叫做无向图的生成树。然后这棵树既然有n-1条边,图当中边是有权重的,这些边的权重之和最小的那棵树就称为无向图的最小生成树

首先对于这个图来说,首先是无向图(说白了也是一种特殊的有向图),然后prim算法适用于稠密图,那既然是稠密图的话,想当然就是用邻接矩阵去存储边。然后对于这个图而言,正权边与负权边无关紧要;最后对于重边和自环,重边的话肯定是取小的,然后环的话是不可能出现在最小生成树当中,需要回避的
int dist[N][N];然后对于这个邻接矩阵初始化操作变成无穷大(等会儿要进行取小操作),然后就是把边输入到这个邻接矩阵当中,无向图的话,实际上就是一种特殊的有向图罢了
memset(g,0x3f3f3f3f,sizeof(g));
int a,b,c;
while(m--)
{scanf("%d %d %d",&a,&b,&c);g[a][b]=g[b][a]=MIN(g[a][b],c);
}然后这是一个很关键的一步,创建一个dist数组,这个dist数组表示每个点到联通块集合的最短距离(这个联通块集合不断壮大壮大,最后就是我的一个最小生成树),在一开始的话,也全部都默认初始化为无穷大
int dist[N];
memset(dist,0x3f,sizeof(dist));除此之外还需要一个数组st起标记作用,就是去说明该点是否已经在联通块集合(这个联通块集合,不断壮大壮大,最后就是我需要求的最小生成树)当中。
int st[N];然后接下来正式就是prim算法,这个prim算法的话与迪杰斯特拉算法非常相似。首先是先去循环n次,然后第一次循环的话,由于是刚刚开始,就选择一号点作为联通快集合的开拓点(真正在联通块集合当中,每一个点没有先来后到之分),然后对于外循环的第一次,他就是仅仅去更新一下别人的dist,并且去标记一下自己已经进入联通块集合当中而已。然后对于接下来的每一次外循环,与Dijkstra算法相似,首先先去找集合外的距离联通块集合距离最近的点,把这个点找到之后。先要去判断一下这个点距离集合的最短距离,如果发现是初始化的那个无穷大值,好那么这时候就说明生成不了最小生成树;如果不是,用这个点所能及更新它所能连接到的其他点的到联通块集合的最短距离并且呢把他自己呢要加入到联通块集合当中(也就是说需要标记一下)。by the way,然后在这个过程当中,我就可以去求我这个最后生成的最小生成树它的各边权重和。
int res=0; //最后生成的最小生成树它的各边权重和
for (int i=0;i<n;i++)
{int t=0;for (int j=1;j<=n;j++){if (st[j]==0 && (t==0 || dist[j]<dist[t])){t=j;}}if (i!=0){if (dist[t]==0x3f3f3f3f){printf("impossible\n");return 0;}else{res+=dist[t];}}st[t]=1;for (int j=1;j<=n;j++){dist[j]=MIN(dist[j],g[t][j]); }}
printf("%d\n",res);例题
来源:AcWing
858. Prim算法求最小生成树 - AcWing题库

#include <stdio.h>
#include <string.h>
#define MIN(a,b) ((a)<(b)?(a):(b))
#define N 510
int g[N][N];
int dist[N];
int st[N];
int main()
{memset(dist,0x3f,sizeof(dist));int n,m;scanf("%d %d",&n,&m);memset(g,0x3f3f3f3f,sizeof(g));int a,b,c;while(m--){scanf("%d %d %d",&a,&b,&c);g[a][b]=g[b][a]=MIN(g[a][b],c);}int res=0;for (int i=0;i<n;i++){int t=0;for (int j=1;j<=n;j++){if (st[j]==0 && (t==0 || dist[j]<dist[t])){t=j;}}if (i!=0){if (dist[t]==0x3f3f3f3f){printf("impossible\n");return 0;}else{res+=dist[t];}}st[t]=1;for (int j=1;j<=n;j++){dist[j]=MIN(dist[j],g[t][j]); }}printf("%d\n",res);return 0;
}相关文章:

(算法基础)朴素版Prim算法
适用情景在最小生成树问题当中,涉及到权重和最小值。并且这个图是稠密图(n^2 ~ m)的情形下时间复杂度O(N^2)算法解释先得知道一下什么是无向图的生成树,树总该知道的吧,生成树就是包含这个无向图中的n个点,并且有n-1条边ÿ…...

第十四届蓝桥杯三月真题刷题训练——第 23 天
目录 第 1 题:长草 题目描述 输入描述 输出描述 输入输出样例 运行限制 代码: 思路: 第 2 题:蓝肽子序列_LCS_最长公共子序列dp问题 题目描述 输入描述 输出描述 输入输出样例 运行限制 代码: 思路&am…...
基于springboot实现医院信息管理系统【源码+论文】
基于springboot实现医院信管系统演示开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包…...
CODESYS增量式PID功能块(ST完整源代码)
增量式PID的详细算法公式和博途源代码,请参看下面的文章链接: 博途1200/1500PLC增量式PID算法(详细SCL代码)_博图scl语言pid增量编码器_RXXW_Dor的博客-CSDN博客SMART200PLC增量式PID可以参看下面这篇博文,文章里有完整的增量式PID算法公式,这里不在赘述西门子SMARTPLC增量…...
代码质量提升,代码扫描 review 之 Codacy 工具使用
目录一、什么是Codacy二、GitHub 上使用 Codacy三、Codacy上导入GitHub项目一、什么是Codacy Codacy 是用于代码 review 检测(即代码审查)的工具,目前支持对40多种编程语言检测,如 c、c、c#、java 、python、javascript 等。 Codacy 可用于 GitHub 和 …...

Centos Linux 正确安装 Redis 的方式
官方文档 Getting started with Redis | Redis 第一步 、下载源代码 源代码的下载方式有很多种,可以去源代码仓库下载,或者使用下面的命令下载 wget https://download.redis.io/redis-stable.tar.gz 第二步 、编译代码 tar -xzvf redis-stable.tar.…...

C++Primer第五版【阅读笔记】
CPrimer第五版 阅读笔记 第1章开始1.1 编写一个简单的C程序1.1.1 编译、运行程序1.2 初识输入输出第1章开始 学习一门新的程序设计语言的最好方法就是练习编写程序。 1.1 编写一个简单的C程序 每个C程序都包含一个或多个函数,其中一个必须命名为 main,…...
ERD Online 4.0.11 在线数据库建模、元数据协作平台(免费、私有部署)
ERD Online 是全球第一个开源、免费在线数据建模、元数据管理平台。提供简单易用的元数据设计、关系图设计、SQL查询等功能,辅以版本、导入、导出、数据源、SQL解析、审计、团队协作等功能、方便我们快速、安全的管理数据库中的元数据。 4.0.11 ❝ :memo: fix(erd):…...

3.数组算法、动态规划
文章目录数组算法1.数组表示2.基本操作3.插入操作算法实例1实例2输出3.删除操作算法实例1输出4.搜索操作算法实例2输出5.更新操作算法实3例输出2.动态规划对照实例1数组算法 Array是一个容器,可以容纳固定数量的项目,这些项目应该是相同的类型。大多数数…...
项目管理工具哪个好?最新排名
项目管理工具当下已经成为项目团队的重要榜首,一款合适好用的项目管理工具可以帮助处理很多机械化工作,将管理者更多精力投入到更有价值的工作中,还可以帮助团队组织和计划项目,跟踪进度,处理预算和协作。该如何挑选帮…...

650. 只有两个键的键盘——【Leetcode每日一题】
650. 只有两个键的键盘 最初记事本上只有一个字符 A 。你每次可以对这个记事本进行两种操作: Copy All(复制全部):复制这个记事本中的所有字符(不允许仅复制部分字符)。Paste(粘贴)…...

【平常心无焦虑探讨】未来谁将被淘汰—在日常网络安全工作中使用GPT的感受
作者:Eason_LYC 悲观者预言失败,十言九中。 乐观者创造奇迹,一次即可。 一个人的价值,在于他所拥有的。所以可以不学无术,但不能一无所有! 技术领域:WEB安全、网络攻防 关注WEB安全、网络攻防。…...
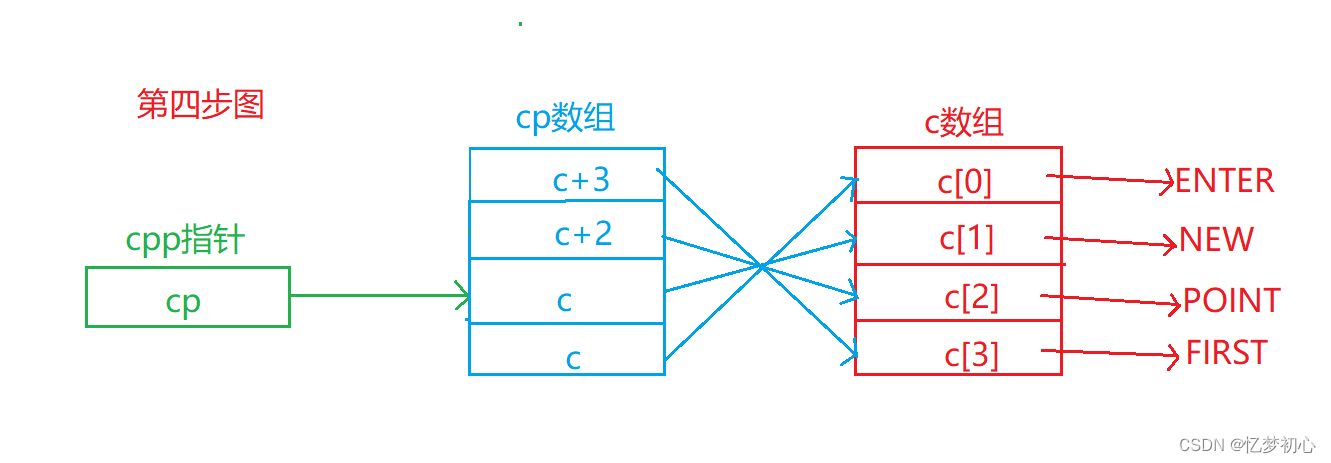
【C语言】深度理解指针(下)
一. 前言💎昨晚整理博客时突然发现指针还少了一篇没写,今天就顺便来补一补。上回书说到,emmm忘记了,没事,我们直接进入本期的内容:本期我们带来了几道指针相关笔试题的解析,还算是相对比较轻松的。话不多说…...

【树与二叉树】树与二叉树的概念及结构--详解介绍
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:数据结构 🎯长路漫漫浩浩,万事皆有期待 文章目录1.树概念及结构1.1 树…...
Spring Boot集成RocketMQ实现普通、延时、事务消息发送接收、PULL消费模式及开启ACL | Spring Cloud 30
一、前言 在前面我们通过以下章节对RocketMQ有了基础的了解: docker-compose 搭建RocketMQ 5.1.0 集群(双主双从模式) | Spring Cloud 28 docker-compose 搭建RocketMQ 5.1.0 集群开启ACL权限控制 | Spring Cloud 29 现在开始我们正式学习…...
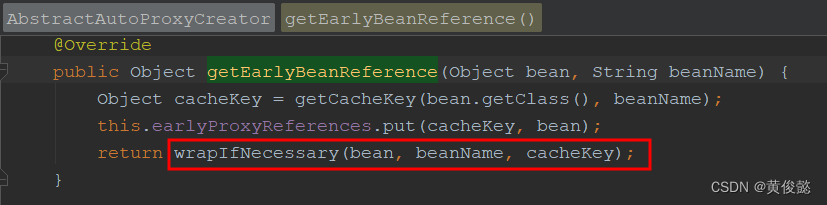
人人都能看懂的Spring源码解析,Spring如何解决循环依赖
人人都能看懂的Spring源码解析,Spring如何解决循环依赖原理解析什么是循环依赖循环依赖会有什么问题?如何解决循环依赖问题的根本原因如何解决为什么需要三级缓存?Spring的三级缓存源码走读Spring的三级缓存提前暴露getSingleton方法总结往期…...

Linux上搭建Discuz论坛
一.准备工作 1.下载php*,mariadb-server 2.上传Discuz3.5压缩包并解压 二.搭建过程 基于redhat 9 版本和Discuz3.5,php8.0,mariadb10.5演示 一.准备工作 1.下载php*,mariadb-server [rootredhat9 aaa]# yum install -y php*…...

【蓝桥杯专题】 树状数组(C++ | 洛谷 | acwing | 蓝桥)
菜狗现在才开始备战蓝桥杯QAQ 文章目录【蓝桥杯专题】 (C | 洛谷 | acwing | 蓝桥)什么是线段数组??1264. 动态求连续区间和数星星线段树AcWing 1270. 数列区间最大值PPPPPPP【蓝桥杯专题】 (C | 洛谷 | acwing | 蓝桥) 什么是…...

QCefView编译配置(Windows-MSVC)(11)
QCefView编译配置(Windows-MSVC) 文章目录QCefView编译配置(Windows-MSVC)1、概述2、准备工作3、添加环境变量4、更换cef源码版本5、CMake构建6、Visual Studio编译7、安装编译后的文件8、验证编译结果更多精彩内容👉个…...

Token原理
Q:分布式场景下如何生成token以及使用token的流程: 在分布式场景下,可以采用以下方式生成 token 和进行权限认证: 1. 生成 token: 使用JWT(JSON Web Token)生成 token。JWT 是一种基于 JSON …...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...
