【树与二叉树】树与二叉树的概念及结构--详解介绍

​

​📝个人主页：@Sherry的成长之路
🏠学习社区：Sherry的成长之路（个人社区）
📖专栏链接：数据结构
🎯长路漫漫浩浩，万事皆有期待

学习顺序
树->二叉树->搜索二叉树->归并排序->M叉多叉平衡搜索树 (B树和B+树)

1.树概念及结构

1.1 树的概念：

树是一种非线性的数据结构，它是由 n (n>=0) 个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下。

1.有一个特殊的结点，称为根结点，根节点没有前驱结点
2. 除根节点外，其余结点被分为 M (M>0) 个互不相交的集合 T1、T2 … 、Tm，其中每一个集合 Ti (1<=i<=m) 又是一棵结构与树类似的子树，每棵子树的根结点有且只有一个前驱，可以有0个或多个后继
3. 因此，树是递归定义的

注意：树形结构中，子树之间不能有交集，否则就不是树形结构
▶ 子树是不相交的
▶ 除了根节点外，每个节点有且仅有一个父节点
▶ 一棵 N 个节点的树有 N-1 条连

1.2 树的相关概念

1.节点的度：一个节点含有的子树的个数称为该节点的度； 如上图：A 的为6
2.叶节点或终端节点：度为0的节点称为叶节点； 如上图：B、C、H、I…等节点为叶节点
3.非终端节点或分支节点：度不为0的节点； 如上图：D、E、F、G…等节点为分支节点
4.双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点； 如上图：A 是 B 的父节点
5.孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点； 如上图：B 是 A 的孩子节点
6.兄弟节点：具有相同父节点的节点互称为兄弟节点 (这里指的是亲兄弟，而非表堂兄弟)； 如上图：B、C 是兄弟节点
7.树的度：一棵树中，最大的节点的度称为树的度； 如上图：树的度为 6
8.节点的层次：从根开始定义起，根为第 1 层，根的子节点为第 2 层， 以此类推；如上图：树的层次为 4
9.树的高度或深度：树中节点的最大层次 (这里有 2 种说法：一，根算 0;二，根算 1)； 如上图：树的高度为 4
  - 这里推荐理解其二，因为：
  当要算空树的高度是多少时，按一的理解，高度是 -1；按二的理解，高度是 0
  当要算只有一个根节点的树的高度是多少时，按一的理解，高度是 0；按二的理解，高度是 1
10.堂兄弟节点：双亲在同一层的节点互为堂兄弟；如上图：H、I 互为兄弟节点
11.节点的祖先：从根到该节点所经分支上的所有节点；如上图：A 是所有节点的祖先
12.子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是 A 的子孙
13.森林：由 m(m>0) 棵互不相交的树的集合称为森林，并查集就是一个森林

1.3 树的表示

树结构相对线性表就比较复杂了，要存储表示起来比较麻烦，既要保存值域，也要保存结点和结点之间的关系。实际中树有很多种表示方式如：双亲表示法，孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。

注意：对于树的定义其实并不好定义，因为其中有许多未知的因素

1、除非明确说明树的度是多少，比如树的度是 6

struct TreeNode
{int data;//这种结构其实是很浪费的，因为最大的度是6,但往下可能并没有那么多struct TreeNode* subs[6];//指针数组
}

2、如果没有说明树的度是多少，可以使用顺序表存储

struct TreeNode
{int data;SeqList subs;//顺序表中存储的是节点的指针//vector<struct TreeNode*>subs;//在C++学了模板后可以这样定义
}

3、双亲表示法

struct TreeNode
{int data;struct TreeNode* parent;
}

4、左孩子右兄弟表示法 (比较实用)

typedef int DataTpye;
struct Node
{struct Node* firstChild1;//第一个孩子节点(如有多个孩子，那么只指向最左边的)struct Node* pNextBrother;//指向下一个兄弟节点DataType data;//节点中的数据域
}

1.3 树在实际中的运用

表示文件系统的目录树结构

2.二叉树概念及结构

2.1 二叉树的概念

一棵二叉树是节点的一个有限集合，该集合：
1、或者为空
2、由一个根节点加上两棵别称为左子树和右子树的二叉树组成

1.二叉树不存在度大于 2 的结点
2.二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树

注意：对于任意的二叉树都是由以下几种情况复合而成的：

2.2 特殊的二叉树

2.2.1 满二叉树：

一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为 K，且结点总数是 2^k - 1，则它就是满二叉树。

2.2.2 完全二叉树：

完全二叉树的前 k - 1 层都满的，第 k 层不一定满(这就意味着满二叉树是完全二叉树，但完全二叉树不一定是满二叉树)，但是从最后一层从左到右必须是连续的，也就是说完全二叉树中度为 1 的节点最少 0 个，最多 1 个。完全二叉树是效率很高的数据结构，是由满二叉树而引出来的。对于深度为 K 的，有 n 个结点的二叉树，且每个结点都与深度为 K 的满二叉树中编号从 1 至 n 的结点 一一 对应称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。

▶ 满二叉树的节点个数是等比求和

2^0 + 2^1 + 2^2 + … 2^(h-1)

利用公式所以满二叉树的节点个数就是 2^h - 1

▶ 完全二叉树的节点个数

最多： 2^h - 1  这是满二叉树

最少：2^(h-1) - 1 + 1  ->  2^(h-1)

2(^h-1) - 1 这是前 k-1 层节点的个数，+1 则是第 k 层至少一个

2.3 二叉树的性质

1.若规定根节点的层数为 1，则一棵非空二叉树的第 i 层上最多有 2^(i-1) 个结点

2.若规定根节点的层数为 1，则深度为 h 的二叉树的最大结点数是2^h - 1

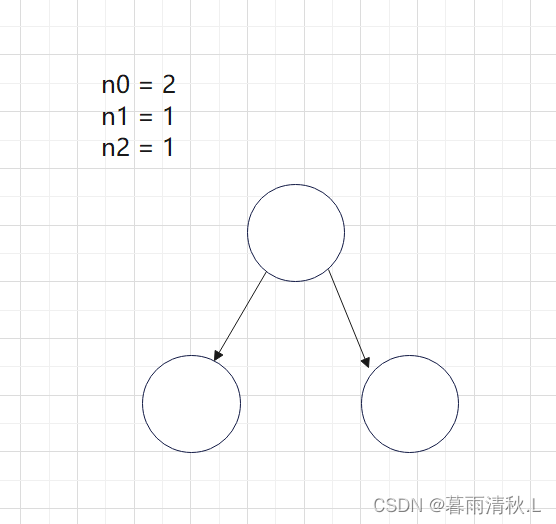
3.对任何一棵二叉树, 如果度为 0 其叶结点个数为 n₀, 度为 2 的分支结点个数为 n₂,则有 n₀＝ n₂＋1

4.若规定根节点的层数为 1，具有 n 个结点的满二叉树的深度为 h = log₂(n+1)  ps：log₂(n+1)是 log 以 2 为底， n+1 的对数

5.对于具有 n 个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从 0 开始编号，则对于序号为 i 的结点有：

▶ 若 i>0，i 位置节点的双亲序号：(i-1)/2；i=0，i 为根节点编号，无双亲节点

▶ 若 2i+1<n，左孩子序号：2i+1，2i+1>=n 否则无左孩子

▶ 若 2i+2<n，右孩子序号：2i+2，2i+2>=n 否则无右孩子

2.4 二叉树的概念选择题

1、某二叉树共有 399 个结点，其中有 199 个度为 2 的节点，则该二叉树中的叶子节点数为（ ）
A. 不存在这样的二叉树
B. 200
C. 198
D. 199

• 分析：这里的叶子节点就是度为 0 的节点，已知二叉树中度为 2 的节点为 199 个，则度为 0 的节点等于度为 2 的节点 +1，所以选择 B 选项

2、下列数据结构中，不适合采用顺序存储结构的是（ ）注意此题可以先了解下面的二叉树的存储结构在来做
A. 非完全二叉树
B. 堆
C. 队列
D. 栈

• 分析：顺序结构存储就是使用数组来存储，它只适合表示完全二叉树，因为不是完全二叉树会有空间的浪费。数组只适合存储完全二叉树或者满二叉树。
  所以选择 A 选项

3、在具有 2n 个节点的完全二叉树中，叶子节点个数为（ ）
A. n
B. n+1
C. n-1
D. n/2

• 分析：
  假设度为 0 的个数是 x0，度为 2 的个数是 x2，度为 1 的个数是 x1，那么：
  ▶ x0 + x1 + x2 = 2n
  ▶ x0 = x2 + 1
  由 x0 = x2 + 1 得到 x2 = x0 - 1
  所以 x0 + x1 + x2 = 2n --> x0 + x1 + x0 - 1 = 2n --> 2x0 + x1 - 1 = 2n
  又因为完全二叉树中度为 1 的节点最少 0 个，最多就只有 1 个，所以 x1 = 0 or 1
  所以 2x0 + x1 - 1 = 2n 就有 2 种情况：
  ▶ 2x0 + 0 - 1 = 2n
  ▶ 2x0 + 1 - 1 = 2n
  当 x1 = 0 时，x0为小数，显然不可能；当 x1 = 1 时满足，所以选择 A 选项

4、一棵完全二叉树的节点数为 531 个，那么这棵树的高度为（ ）
A. 11
B. 10
C. 8
D. 12

• 分析：
  假设完全二叉树的高度是 h，那么：最多有 2^h-1 个节点；最少有 2^(h-1) 个节点
  ▶ h = 11 时：最多 2047；最少 2014，所以不合理
  ▶ h = 10 时：最多 1023；最少 512，所以合情合理
  ▶ h = 8 时：最多 255；最少 128，所以不合理
  ▶ h = 12 时：最多 4095；最少 2048，所以不合理
  所以选择 B 选项

5、一个具有 767 个节点的完全二叉树，其叶子节点个数为 ( )
A. 383
B. 384
C. 385
D. 386

• 分析：此题类似于第 3 题
  假设度为 0 的个数是 x0，度为 2 的个数是 x2，度为 1 的个数是 x1，那么：
  ▶ x0 + x1 + x2 = 767
  ▶ x0 = x2 + 1
  由 x0 = x2 + 1 得到 x2 = x0 - 1
  所以 x0 + x1 + x2 = 767 同 x0 + x1 + x0 - 1 = 767 同 2x0 + x1 - 1 = 767
  完全二叉树中度为 1 的节点最少 0 个，最多就只有 1 个
  所以 x1 = 0 or 1
  所以 2x0 + x1 - 1 = 767 就有 2 种情况：
  ▶ 2x0 + 0 - 1 = 767
  ▶ 2x0 + 1 - 1 = 767
  当 x1 = 0 时，满足条件；当 x1 = 1 时，不满足条件，所以选择 B 选项

2.5 二叉树的存储结构

二叉树一般可以使用两种结构存储，一种顺序结构，一种链式结构：

2.5.1. 顺序存储：

顺序结构存储就是使用数组来存储，它只适合表示完全二叉树，因为不是完全二叉树会有空间的浪费。而现实使用中只有堆才会使用数组来存储，二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树。如下图所见，数组只适合存储完全二叉树或者满二叉树。

怎么表示二叉树的值在数组位置中父子下标关系的：

左孩子和右孩子
leftchild = parent * 2 + 1
rightchild = parent * 2 + 2

父亲 (这里无论是左孩子还是右孩子都适用于以下公式)
parent = (child - 1) / 2

2.5.2. 链式存储：

二叉树的链式存储结构是指用链表来表示一棵二叉树，即用链表来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链的存储地址。

链式结构又分为二叉链和三叉链，现阶段本篇文章我们只了解二叉链，在以后的文章内写到高阶数据结构时，如红黑树等会用到三叉链。

二叉链只能通过父亲找孩子，类似于单向链表；而三叉链不仅能通过父亲找孩子，还能通过孩子找父亲，类似于双向链表。

typedef int BTDataType;
//二叉链
struct BinaryTreeNode
{struct BinaryTreeNode* _pLeft; //指向当前节点的左孩子struct BinaryTreeNode* _pRight; //指向当前节点的右孩子	BTDataType _data; //当前节点的值域 
}//三叉链
struct BinaryTreeNode
{struct BinaryTreeNode* _pParent; //指向当前节点的父亲struct BinaryTreeNode* _pLeft; //指向当前节点的左孩子struct BinaryTreeNode* _pRight; //指向当前节点的右孩子BTDataType _data; //当前节点的值域
}

3.总结：

今天我们认识并学习了树与二叉树的相关概念，对树与二叉树有了一个整体的认识。并且对二叉树的两种存储结构也有了一定的了解。下一篇博客我们将学习二叉树顺序结构和实现以及堆的概念及结构。希望我的文章和讲解能对大家的学习提供一些帮助。

当然，本文仍有许多不足之处，欢迎各位小伙伴们随时私信交流、批评指正！我们下期见~