树和二叉树
树
节点(Node:)
树由一系列的节点组成,每个节点可以包含数据和指向其他节点的链接。
节点通常包含一个数据元素和若干指向其他节点的指针
根节点(Root):
树的顶部节点称为根节点,它是树中没有父节点的唯一节点
子节点(Child):
一个节点的子节点是指由该节点直接指向的节点
叶节点(Leaf):
没有子节点的节点称为叶节点或终端节点
深度(Depth):
节点的深度是从根节点到该节点的路径上的边数。
(广)度:
最大的节点的度
二叉树
每个节点最多有两个子节点的树,通常称为左子节点和右子节点
满二叉树:
在不增加层数的情况下,不能再增加节点了,即为满二叉树
第K层节点个数:
2^(k-1)
K层满二叉树:
总结点数:2^K - 1
完全二叉树:
在满二叉树的基础下,删除节点,只能从右至左,从下到上,删若干个
添加节点,只能从左至右,从上到下,添加若干个。
满二叉树一定是完全二叉树
完全二叉树不一定是满二叉树
二叉树的遍历
前序遍历:先遍历根,再遍历左子树然后再遍历右子树

中序遍历:先遍历左子树,再遍历根,再遍历右子树

后序遍历:先遍历左子树,再遍历右子树,最后遍历根

层序遍历:从上到下,从左至右,逐层遍历
前三种称为深度优先,层序遍历称为广度优先
已知一种排序,不能还原出唯一的二叉树
已知前序+中序 --->唯一的二叉树
已知后序+中序 --->唯一的二叉树
但是知道前序和后序不能还原
二叉树相关练习
1.创建二叉树
TNode_t *create_bin_tree()
{TDataType data = tree[idx++];if(data == '#'){return NULL;}TNode_t *pnode = malloc(sizeof(TNode_t));if(NULL == pnode){perror("malloc fail");return NULL;}pnode->data = data;pnode->pl = create_bin_tree();pnode->pr = create_bin_tree();return pnode;
}2.前序遍历
void pre_order(TNode_t *proot)
{if(NULL == proot){return;}printf("%c",proot->data);pre_order(proot->pl);pre_order(proot->pr);
}3.中序遍历
void mid_order(TNode_t *proot)
{if(NULL == proot){return;}mid_order(proot->pl);printf("%c",proot->data);mid_order(proot->pr);
}
4.后序遍历
void last_order(TNode_t *proot)
{if(NULL == proot){return;}last_order(proot->pl);last_order(proot->pr);printf("%c",proot->data);
}5.层序遍历
void layer_order(TNode_t *pnode)
{Queue_t *qnode = create_queue();if(NULL == qnode){return;}push_queue(qnode,(QDataType)pnode);while(!is_empty_queue(qnode)){QDataType outdata;if(pop_queue(qnode,&outdata) == 0){TNode_t *node = (TNode_t *)outdata;printf("%c",outdata->data);if(node->pl){push_queue(qnode,(QDataType)node->pl);}if(node->pr){push_queue(qnode,(QDataType)node->pr);}}}destory_queue(qnode);
}6.获取二叉树节点数
int get_tree_node(TNode_t *proot)
{if(NULL == proot){return 0;}num++;get_tree_node(proot->pl);get_tree_node(proot->pr);return num;
}7.获取二叉树层数
int get_tree_fl(TNode_t *proot)
{if(NULL == proot){return 0;}int cntl = get_tree_fl(proot->pl);int cntr = get_tree_fl(proot->pr);return cntl > cntr ? cntl + 1 : cntr + 1;
}//二叉树的相关函数,例如创建二叉树,前序,后序,中序等都是基于一个函数递归调用的思想,原因是,树本身就是一个递归的结构,由根节点和子节点构成,所以写写树相关的代码时离不了相关函数的递归调用。不过值得一提的是,函数的递归调用的执行效率并不高。
相关文章:

树和二叉树
树 节点(Node:) 树由一系列的节点组成,每个节点可以包含数据和指向其他节点的链接。 节点通常包含一个数据元素和若干指向其他节点的指针 根节点(Root): 树的顶部节点称为根节点,…...
一篇带你速通差分算法(C/C++)
个人主页:摆烂小白敲代码 创作领域:算法、C/C 持续更新算法领域的文章,让博主在您的算法之路上祝您一臂之力 欢迎各位大佬莅临我的博客,您的关注、点赞、收藏、评论是我持续创作最大的动力 差分算法是一种在计算机科学中常用的算法…...

贷款利率高低跟什么有关?仅凭身份证就能贷到款?额度是多少?
在金融的广阔舞台上,借款人的“信用基石”——即其综合资质,是决定贷款利率高低的决定性因素。这并非偶然,而是银行基于详尽的风险评估与收益预期所做出的精准判断。 需明确的是,贷款的易得性并不意味着无门槛的放任。它更像是设置…...

苹果电脑需要安装杀毒软件吗?探索Mac的安全世界!
在聊到电脑安全时,许多Mac用户都骄傲地声称:“我的Mac是不会中病毒的!”确实,与Windows PC相比,Mac因其UNIX-based的操作系统构架,天生就更加安全。但这是否意味着Mac完全不需要杀毒软件呢?让我…...

Oracle start with connect BY 死循环
解决办法 检查start with前有没有where条件, 如果有的话,套一层select,再 Oracle start with connect BY...

力扣接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表…...

bug“医典”
温馨提示:本篇文章主要用于收藏博主所遇到的各种bug,并且不定期更新 目录 未初始化 “病状” “处方” 数组越界 “病状” “处方” 未创建对象 “病状” 编辑 “处方” 未初始化 “病状” 这种是处在链表中的一种情况,通常是没有处理哨兵位…...

Track 06:量子计算机概述
量子计算机概述 量子计算机是基于量子力学原理的一种计算机,它与传统的经典计算机在处理信息的方式上有根本性的区别。量子计算机的设计和实现依赖于量子比特(qubits)和量子计算的核心概念,如叠加态和纠缠态,这些特性使其在解决某些复杂问题时具备传统计算机无法比拟的优…...

论文解读 | KDD2024 演化图上的森林矩阵快速计算
点击蓝字 关注我们 AI TIME欢迎每一位AI爱好者的加入! 点击 阅读原文 观看作者直播讲解回放! 作者简介 孙浩鑫,复旦大学博士生,主要研究方向为大规模图上快速算法设计。 概述 森林矩阵在网络科学、观点动力学和机器学习相关应用中…...
7.统一网关-Gateway
文章目录 1.统一网关介绍2.网关开发3.predicate4.Route Predicate Factories(路由断言工厂)4.1Path 路由断言工厂4.2.Method 路由断言工厂4.3 Header 路由断言工厂4.4 Query 路由断言工厂4.5 Host 路由断言工厂4.6 After 路由断言工厂4.7 Before 路由断言工厂4.8 Between 路由断…...

QT:QWidget 控件属性的介绍
控件属性介绍 🌴enabled 状态属性🌴geometry 几何属性示例一:改变控件尺寸示例二:更变控件位置window frame 的影响 🌴windowTitle 窗口标题🌴windowIcon 窗口图标🌴 qrc机制🌴windo…...

ctfshow-nodejs
什么是nodejs Node.js 是一个基于 Chrome V8 引擎的 Javascript 运行环境。可以说nodejs是一个运行环境,或者说是一个 JS 语言解释器 Nodejs 是基于 Chrome 的 V8 引擎开发的一个 C 程序,目的是提供一个 JS 的运行环境。最早 Nodejs 主要是安装在服务器…...

Linux 大文件和大量小文件的复制策略
在Linux上复制大文件或大量小文件时,可以根据文件的类型、数量以及硬件配置(如硬盘类型、CPU、内存)选择不同的复制策略,以提高复制效率。以下是一些常见的策略和工具,可以根据具体情况使用: 1. 大文件复制…...

0.3 学习Stm32经历过的磨难
文章目录 用库函数传参 能否按位或STM32库函数XXX_GetFlagStatus和XXX_GetITStatus的区别关于MDK导入文件后报错 Browse information of one files is not available用exti中断读取按键 忘记消抖 (更离谱的是,我忘记开启afio的时钟了 Damn!)D…...
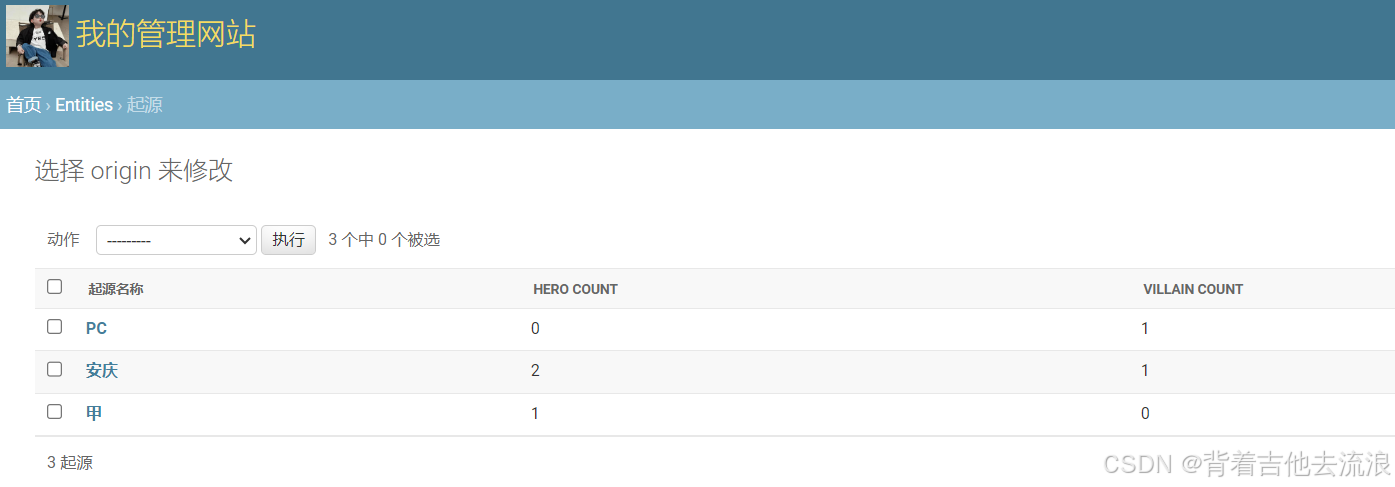
9、Django Admin优化查询
如果你的Admin后台中有很多计算字段,那么你需要对每个对象运行多个查询,这会使你的Admin后台变得非常慢。要解决此问题,你可以重写管理模型中的get_queryset方法使用annotate聚合函数来计算相关的字段。 以下示例为Origin模型的中ModelAdmin…...
—二分法》)
数据结构基础之《(3)—二分法》
一、认识二分法 1、经常见到的类型是在一个有序数组上,开展二分搜索 2、但有序真的是所有问题求解时使用二分的必要条件吗?不 3、只要能正确构建左右两侧的淘汰逻辑,你就可以二分 二、二分法怎么用 1、在一个有序数组中,找某个…...
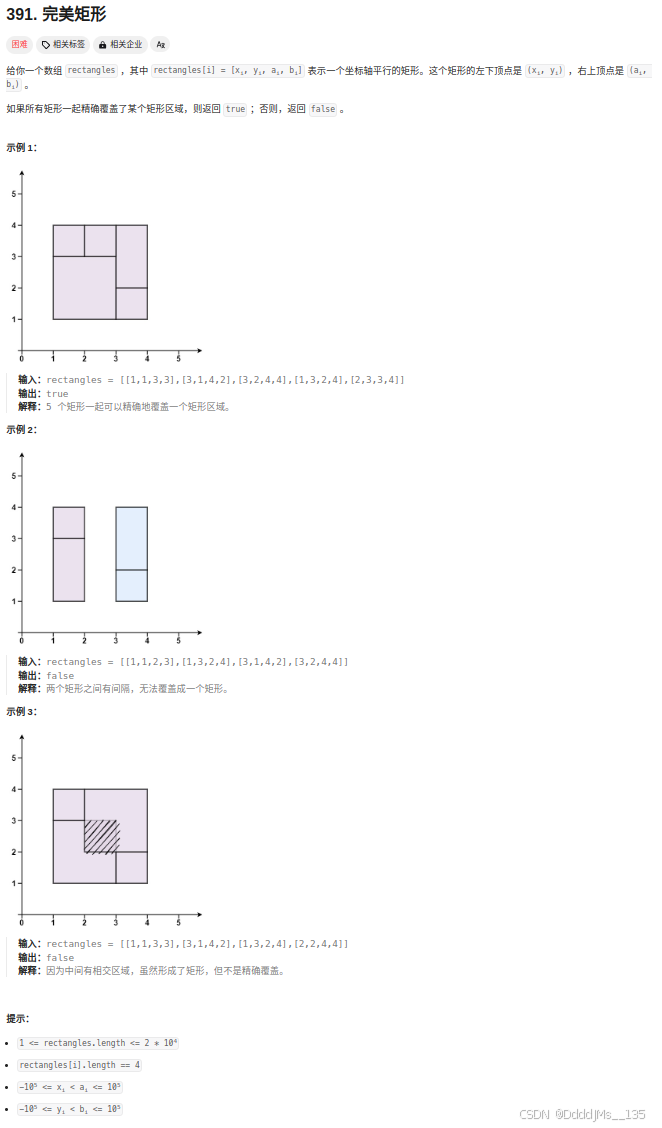
C语言 | Leetcode C语言题解之第391题完美矩形
题目: 题解: bool isSubsequence(char* s, char* t) {int mstrlen(s); int nstrlen(t);int k0; int j0;if(mn&&m0) return true;for(int i0;i<n;i){if(s[j]t[i]){j;}if(jm) return true;}return false; }...
day47——面向对象特征之继承
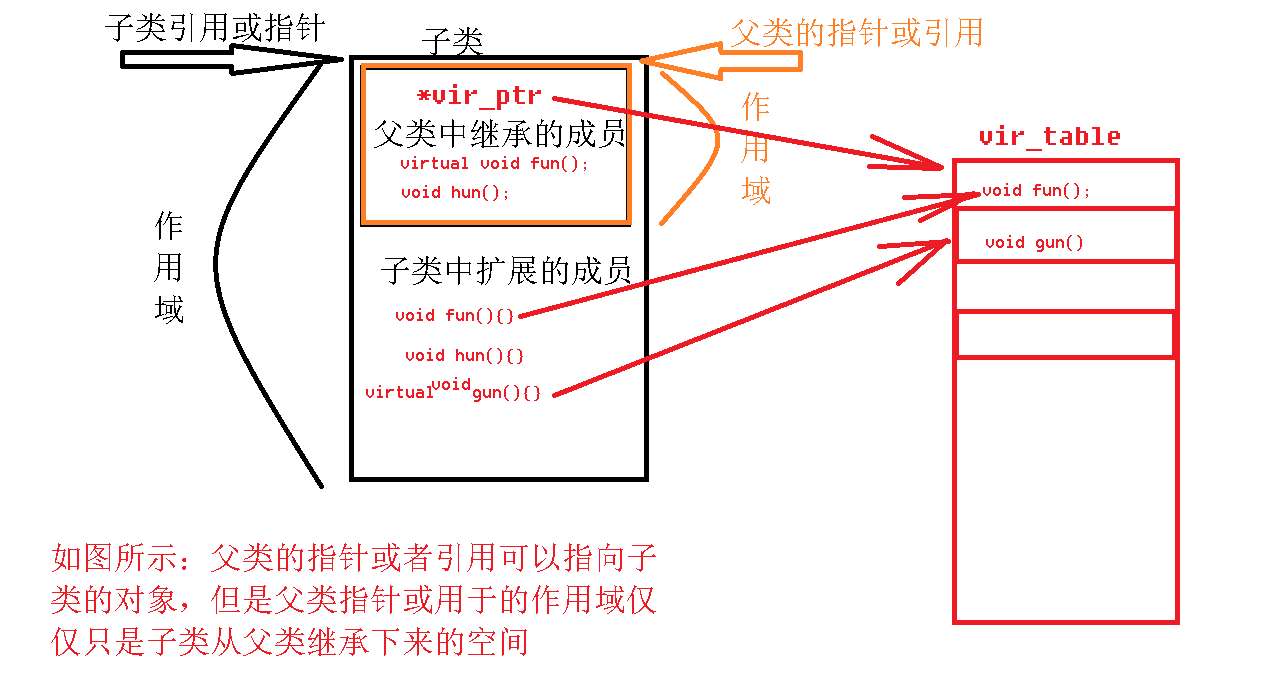
一、继承(inhert) 面向对象三大特征:封装、继承、多态 继承:所谓继承,是类与类之间的关系。就是基于一个已有的类,来创建出一个新类的过程叫做继承。主要提高代码的复用性。 1.1 继承的作用 1> 实现…...

启动 Spring Boot 项目时指定特定的 application.yml 文件位置
java -jar your-spring-boot-app.jar --spring.config.locationfile:/path/to/your/config/application.yml your-spring-boot-app.jar 是你的 Spring Boot 应用的 JAR 文件名。file:/path/to/your/config/application.yml 是配置文件的绝对路径。 如果你有多个配置文件&#…...
Hive 本地启动时报错 Persistence Manager has been closed
Hive 本地启动时报错 Persistence Manager has been closed 2024-09-07 17:21:45 ERROR RetryingHMSHandler:215 - Retrying HMSHandler after 2000 ms (attempt 2 of 10) with error: javax.jdo.JDOFatalUserException: Persistence Manager has been closedat org.datanucle…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
