贷款利率高低跟什么有关?仅凭身份证就能贷到款?额度是多少?
在金融的广阔舞台上,借款人的“信用基石”——即其综合资质,是决定贷款利率高低的决定性因素。这并非偶然,而是银行基于详尽的风险评估与收益预期所做出的精准判断。

需明确的是,贷款的易得性并不意味着无门槛的放任。它更像是设置了一个更为宽泛的准入标准,让多样化的借款人能够有机会尝试,但能否真正获得贷款,还需依据个人的经济实力、职业稳定性及信用历史的纯净度来综合评判。银行的核心考量始终在于确保资金的安全回收,因此,对借款人的还款能力有着严格的审视。
谈及信用贷款,它绝非仅凭身份信息的简单交易,而是对个体信用价值的深度挖掘与量化评估。这一过程涉及信用评分的考量、收入证明的力度以及实际还款能力的验证。市场上的“仅凭身份证贷款”宣传,往往带有误导性,真实的信用贷款远比这复杂且严谨。

在踏上贷款之旅前,自我审视是至关重要的一步。如何判断自身是否符合贷款条件?以下几点不可忽视:
- 信用自查:征信报告如同个人的金融身份证,其清洁度直接关乎贷款申请的成败。优质的征信记录是打开贷款大门的金钥匙。
- 收入评估:确保月收入足以覆盖贷款月供的至少两倍,这是银行衡量还款能力的基本标尺。
- 负债审视:过高的负债如同背负的巨石,会显著增加贷款申请的风险,影响审批结果。
- 资产盘点:拥有稳定的资产支撑,能显著提升贷款申请的成功率与额度。
- 诚信为本:提交真实无误的申请材料,是每位借款人应遵循的基本原则,任何欺诈行为都将面临法律的严惩。
当前,国家正积极推行普惠金融政策,旨在提升金融服务的覆盖面与包容性,但这并不意味着贷款门槛的降低或标准的放宽。普惠金融强调的是公平性与可触及性,而贷款审批依然遵循严格的规则与流程。
至于贷款利率,它并非一成不变,而是根据个人资质、贷款期限及风险评估等多重因素动态调整。优质借款人能够享受更低的利率优惠,而风险较高的借款人则需承担更高的利息成本。这既是对风险的有效定价,也是银行与借款人之间双赢合作的基础。

因此,在申请贷款之前,做好充分的规划与准备至关重要。通过维护良好的信用记录、保持稳定的收入来源、控制合理的负债水平、积累坚实的资产基础以及提交真实的申请材料,将大大提升贷款申请的成功率与获得更优惠利率的可能性。在金融的航道上,深入理解并遵循这些规则,将是我们顺利前行的有力保障。
相关文章:

贷款利率高低跟什么有关?仅凭身份证就能贷到款?额度是多少?
在金融的广阔舞台上,借款人的“信用基石”——即其综合资质,是决定贷款利率高低的决定性因素。这并非偶然,而是银行基于详尽的风险评估与收益预期所做出的精准判断。 需明确的是,贷款的易得性并不意味着无门槛的放任。它更像是设置…...

苹果电脑需要安装杀毒软件吗?探索Mac的安全世界!
在聊到电脑安全时,许多Mac用户都骄傲地声称:“我的Mac是不会中病毒的!”确实,与Windows PC相比,Mac因其UNIX-based的操作系统构架,天生就更加安全。但这是否意味着Mac完全不需要杀毒软件呢?让我…...

Oracle start with connect BY 死循环
解决办法 检查start with前有没有where条件, 如果有的话,套一层select,再 Oracle start with connect BY...

力扣接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表…...

bug“医典”
温馨提示:本篇文章主要用于收藏博主所遇到的各种bug,并且不定期更新 目录 未初始化 “病状” “处方” 数组越界 “病状” “处方” 未创建对象 “病状” 编辑 “处方” 未初始化 “病状” 这种是处在链表中的一种情况,通常是没有处理哨兵位…...

Track 06:量子计算机概述
量子计算机概述 量子计算机是基于量子力学原理的一种计算机,它与传统的经典计算机在处理信息的方式上有根本性的区别。量子计算机的设计和实现依赖于量子比特(qubits)和量子计算的核心概念,如叠加态和纠缠态,这些特性使其在解决某些复杂问题时具备传统计算机无法比拟的优…...

论文解读 | KDD2024 演化图上的森林矩阵快速计算
点击蓝字 关注我们 AI TIME欢迎每一位AI爱好者的加入! 点击 阅读原文 观看作者直播讲解回放! 作者简介 孙浩鑫,复旦大学博士生,主要研究方向为大规模图上快速算法设计。 概述 森林矩阵在网络科学、观点动力学和机器学习相关应用中…...
7.统一网关-Gateway
文章目录 1.统一网关介绍2.网关开发3.predicate4.Route Predicate Factories(路由断言工厂)4.1Path 路由断言工厂4.2.Method 路由断言工厂4.3 Header 路由断言工厂4.4 Query 路由断言工厂4.5 Host 路由断言工厂4.6 After 路由断言工厂4.7 Before 路由断言工厂4.8 Between 路由断…...

QT:QWidget 控件属性的介绍
控件属性介绍 🌴enabled 状态属性🌴geometry 几何属性示例一:改变控件尺寸示例二:更变控件位置window frame 的影响 🌴windowTitle 窗口标题🌴windowIcon 窗口图标🌴 qrc机制🌴windo…...

ctfshow-nodejs
什么是nodejs Node.js 是一个基于 Chrome V8 引擎的 Javascript 运行环境。可以说nodejs是一个运行环境,或者说是一个 JS 语言解释器 Nodejs 是基于 Chrome 的 V8 引擎开发的一个 C 程序,目的是提供一个 JS 的运行环境。最早 Nodejs 主要是安装在服务器…...

Linux 大文件和大量小文件的复制策略
在Linux上复制大文件或大量小文件时,可以根据文件的类型、数量以及硬件配置(如硬盘类型、CPU、内存)选择不同的复制策略,以提高复制效率。以下是一些常见的策略和工具,可以根据具体情况使用: 1. 大文件复制…...

0.3 学习Stm32经历过的磨难
文章目录 用库函数传参 能否按位或STM32库函数XXX_GetFlagStatus和XXX_GetITStatus的区别关于MDK导入文件后报错 Browse information of one files is not available用exti中断读取按键 忘记消抖 (更离谱的是,我忘记开启afio的时钟了 Damn!)D…...
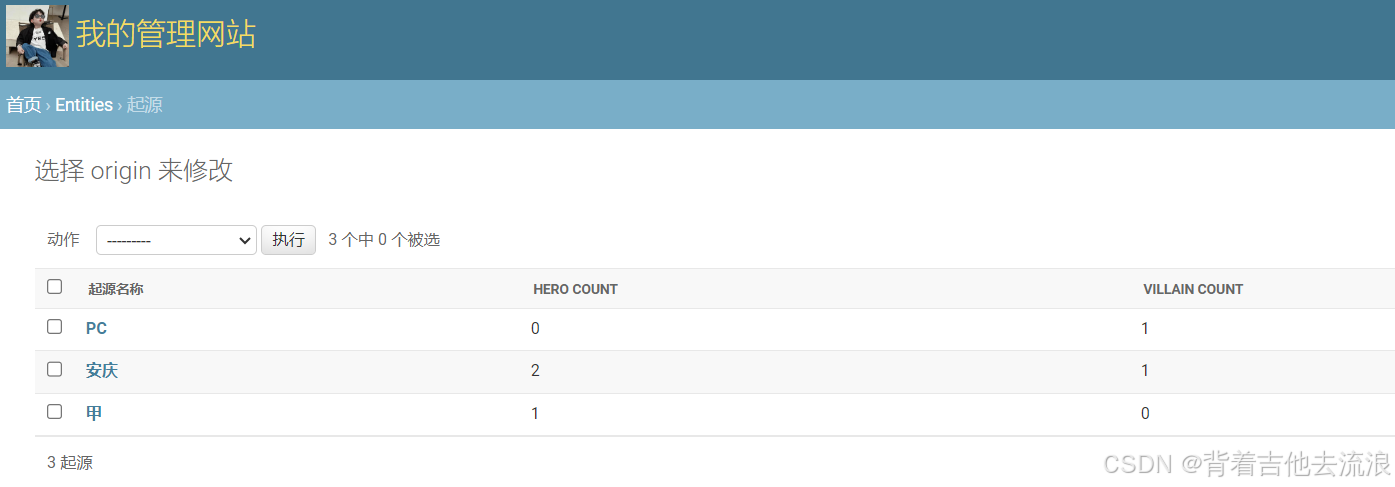
9、Django Admin优化查询
如果你的Admin后台中有很多计算字段,那么你需要对每个对象运行多个查询,这会使你的Admin后台变得非常慢。要解决此问题,你可以重写管理模型中的get_queryset方法使用annotate聚合函数来计算相关的字段。 以下示例为Origin模型的中ModelAdmin…...
—二分法》)
数据结构基础之《(3)—二分法》
一、认识二分法 1、经常见到的类型是在一个有序数组上,开展二分搜索 2、但有序真的是所有问题求解时使用二分的必要条件吗?不 3、只要能正确构建左右两侧的淘汰逻辑,你就可以二分 二、二分法怎么用 1、在一个有序数组中,找某个…...
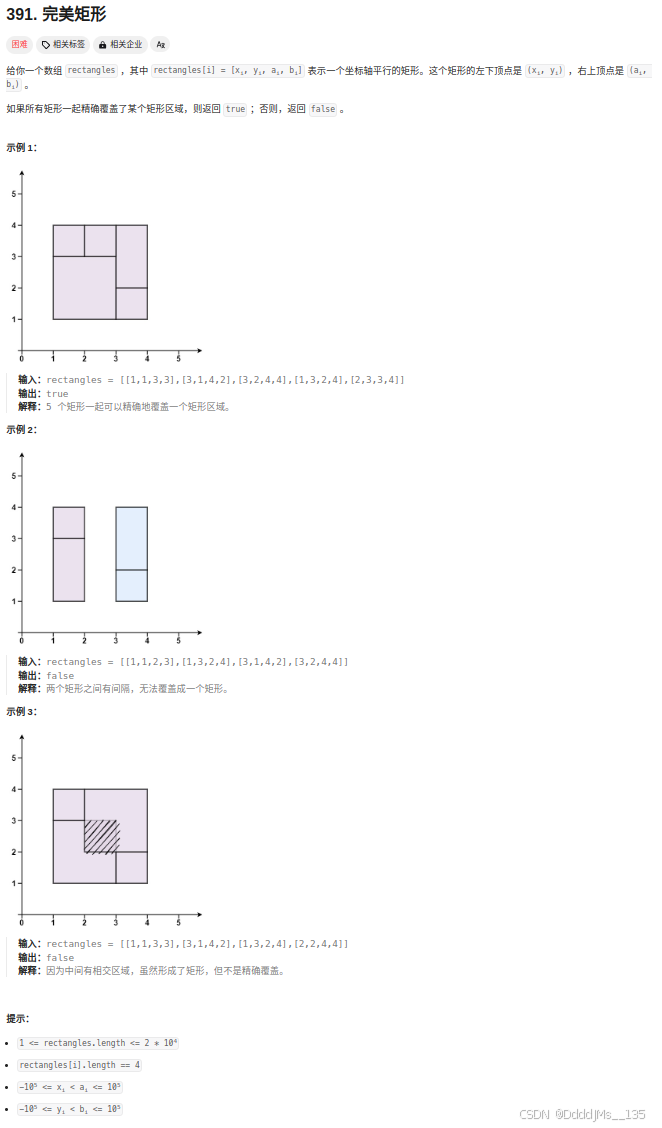
C语言 | Leetcode C语言题解之第391题完美矩形
题目: 题解: bool isSubsequence(char* s, char* t) {int mstrlen(s); int nstrlen(t);int k0; int j0;if(mn&&m0) return true;for(int i0;i<n;i){if(s[j]t[i]){j;}if(jm) return true;}return false; }...
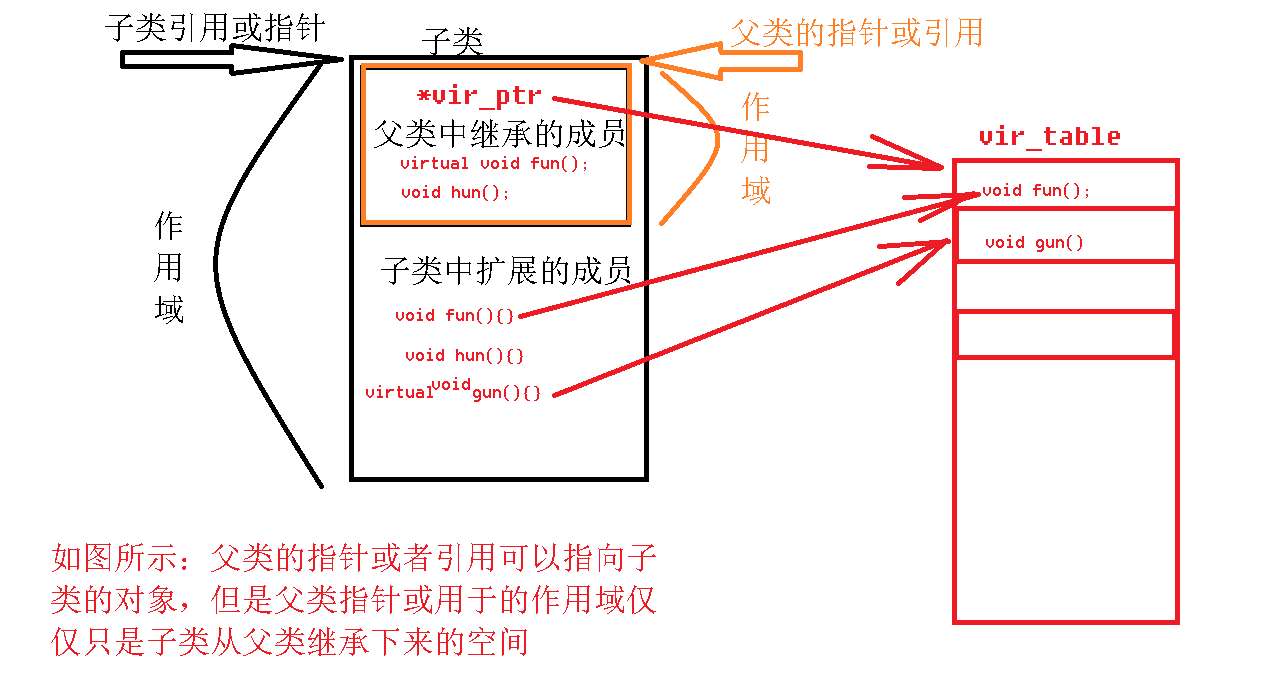
day47——面向对象特征之继承
一、继承(inhert) 面向对象三大特征:封装、继承、多态 继承:所谓继承,是类与类之间的关系。就是基于一个已有的类,来创建出一个新类的过程叫做继承。主要提高代码的复用性。 1.1 继承的作用 1> 实现…...

启动 Spring Boot 项目时指定特定的 application.yml 文件位置
java -jar your-spring-boot-app.jar --spring.config.locationfile:/path/to/your/config/application.yml your-spring-boot-app.jar 是你的 Spring Boot 应用的 JAR 文件名。file:/path/to/your/config/application.yml 是配置文件的绝对路径。 如果你有多个配置文件&#…...
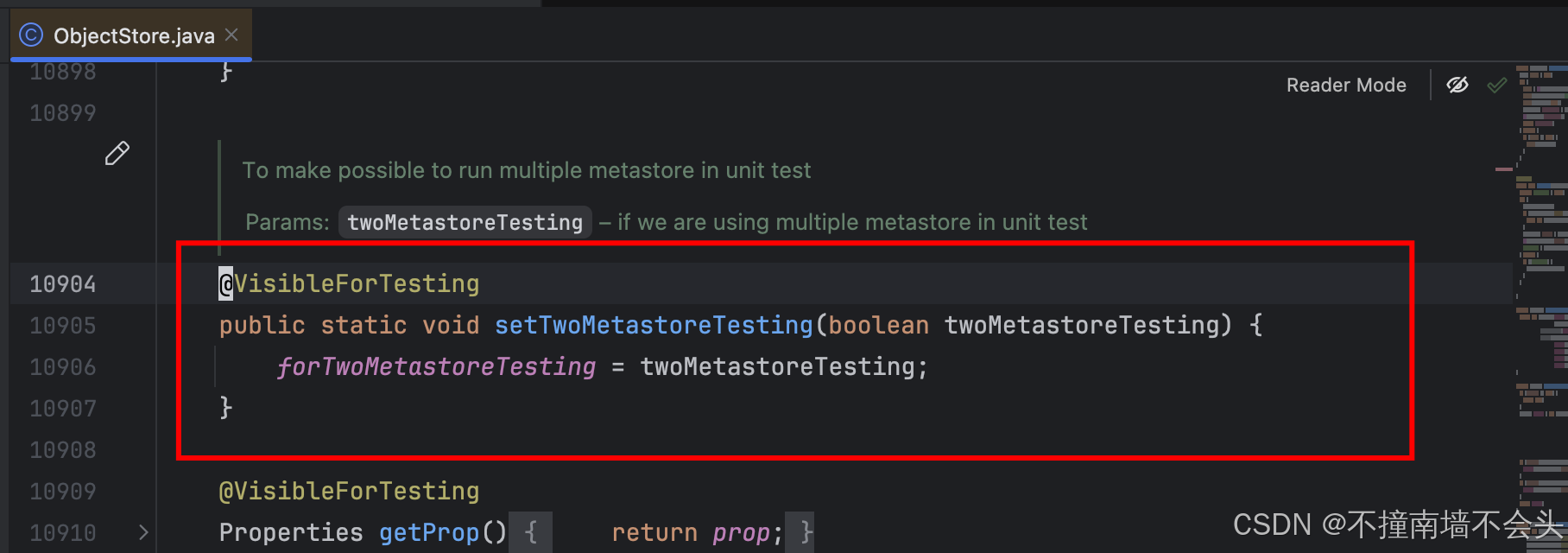
Hive 本地启动时报错 Persistence Manager has been closed
Hive 本地启动时报错 Persistence Manager has been closed 2024-09-07 17:21:45 ERROR RetryingHMSHandler:215 - Retrying HMSHandler after 2000 ms (attempt 2 of 10) with error: javax.jdo.JDOFatalUserException: Persistence Manager has been closedat org.datanucle…...

多模态在京东内容算法上的应用
多模态在京东内容算法上的应用 作者:京东零售技术 2024-09-04 北京 本文字数:5226 字 阅读完需:约 17 分钟 本文作者唐烨参与 DataFunsummit2024:推荐系统架构峰会,在专题【多模态推荐论坛】中分享了多模态算法在京…...

SSM+Ajax实现广告系统
文章目录 1.案例需求2.编程思路3.案例源码(这里只给出新增部分的Handler和ajax部分,需要详情的可以私信我)4.小结 1.案例需求 使用SSMAjax实现广告系统,包括登录、查询所有、搜索、新增、删除、修改等功能,具体实现的效果图如下:…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...
