70. 爬楼梯
70. 爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
1.1 阶 + 1 阶
2.2 阶
示例 2:
输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。
1.1 阶 + 1 阶 + 1 阶
2.1 阶 + 2 阶
3.2 阶 + 1 阶
提示:
1 <= n <= 45
解题思路
①状态表示:1.集合f[i]表示的是到达i阶台阶时,所拥有的方案数。2.操作:求+。
②状态计算:我们考虑i,i层台阶可以i-1层台阶和i-2层台阶得到,由于到达两者的目的并不相同,因此这两种方案数量相加即可
③初始状态 :f [1]=1, f[2] =2
代码
class Solution {
public:int climbStairs(int n) {if(n<=1) return n;vector<int> f(n+1);//开n+1防止数组越界f[1]=1,f[2]=2;for(int i=3;i<=n;i++){f[i]=f[i-1]+f[i-2];}return f[n];}
};
相关文章:

70. 爬楼梯
70. 爬楼梯 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 示例 1: 输入:n 2 输出:2 解释:有两种方法可以爬到楼顶。 1.1 阶 1 阶 2.2 阶 示例…...
使定义的神经网络中权重参数变为nan)
pytorch正向传播没问题,loss.backward()使定义的神经网络中权重参数变为nan
记录一个非常坑爹的bug:loss回传导致神经网络中一个linear层的权重参数变为nan 1.首先loss值是正常数值; 2.查了好多网上的解决办法:检查原始输入神经网络数据有没有nan值,初始化权重参数,使用relu激活函数,梯度裁剪&a…...

❤《实战纪录片 1 》原生开发小程序中遇到的问题和解决方案
《实战纪录片 1 》原生开发小程序中遇到的问题和解决方案 文章目录 《实战纪录片 1 》原生开发小程序中遇到的问题和解决方案1、问题一:原生开发中 request请求中返回 的数据无法 使用this传递给 data{}中怎么办?2、刚登录后如何将token信息保存…...

2024.9.6 作业
手写unique_ptr指针指针 代码: #include <iostream> #include <stdexcept>template <typename T> class unique_ptr { public:// 构造函数explicit unique_ptr(T* ptr nullptr) : m_ptr(ptr) {}// 析构函数~unique_ptr() {delete m_ptr;}// 禁…...

2024年架构设计师论文-“模型驱动架构设计方法及其应用”
论模型驱动架构设计方法及其应用 模型驱动架构设计是一种用于应用系统开发的软件设计方法,以模型构造、模型转换和精化为核心,提供了一套软件设计的指导规范。在模型驱动架构环境下,通过创建出机器可读和高度抽象的模型实现对不同问题域的描述…...

Tapd敏捷开发平台的使用心得
Tapd敏捷开发平台的使用心得 一、Tapd 简介 TAPD(Tencent Agile Product Development),腾讯敏捷产品研发平台行业领先的敏捷协作方案,贯穿敏捷产品研发生命周期的一站式服务,了解敏捷如下图 二、几个核心模块概念 需求迭代缺陷故事墙前期项目需求的管理,可以按类别建…...

远程桌面 Rust Desk 自建服务器
因为某些原因(诈骗),Rush Desk 服务已暂停国内访问,今天我们介绍如何利用自己的服务器搭建 Rust Desk 远程桌面,低延迟电脑远程手机,手机远程电脑等 一、准备工作 准备一台服务器,我用的腾讯云服务器,一年…...
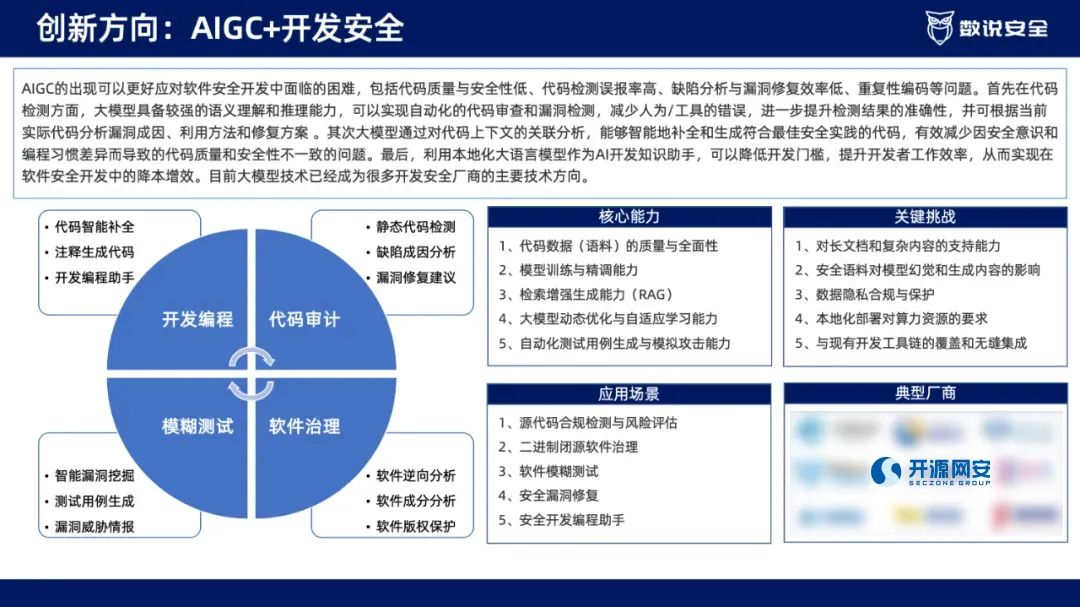
开源网安引领AIGC+开发安全,智能防护铸就软件安全新高度
近日,国内网络安全领域知名媒体数说安全正式发布了《2024年中国网络安全市场100强》和《2024年中国网络安全十大创新方向》。开源网安凭借在市场表现力、资源支持力以及产品在AI方向的创新力上的优秀表现成功入选百强榜单,并被评为“AIGC开发安全”典型厂…...

树和二叉树
树 节点(Node:) 树由一系列的节点组成,每个节点可以包含数据和指向其他节点的链接。 节点通常包含一个数据元素和若干指向其他节点的指针 根节点(Root): 树的顶部节点称为根节点,…...
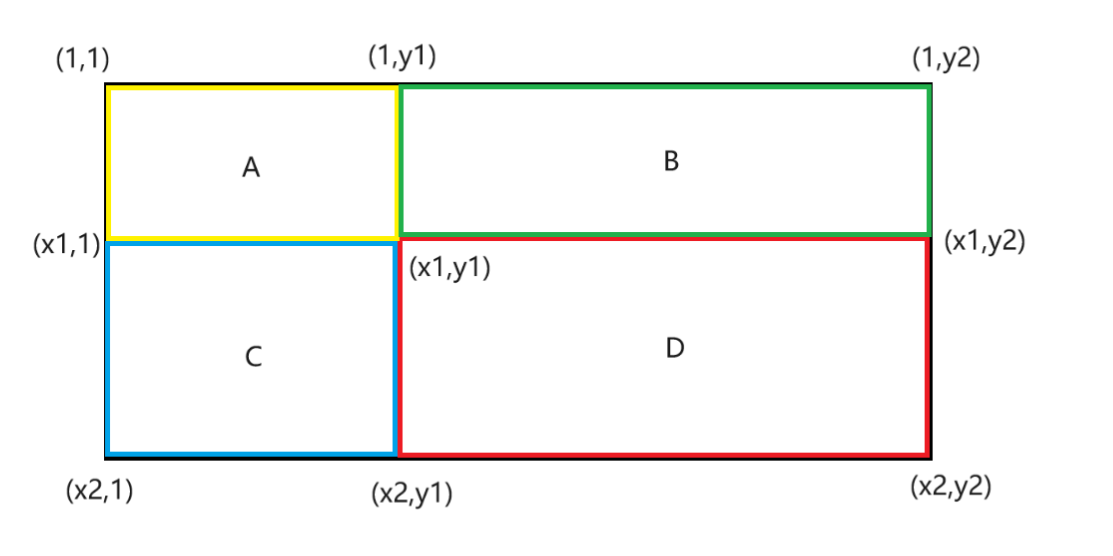
一篇带你速通差分算法(C/C++)
个人主页:摆烂小白敲代码 创作领域:算法、C/C 持续更新算法领域的文章,让博主在您的算法之路上祝您一臂之力 欢迎各位大佬莅临我的博客,您的关注、点赞、收藏、评论是我持续创作最大的动力 差分算法是一种在计算机科学中常用的算法…...

贷款利率高低跟什么有关?仅凭身份证就能贷到款?额度是多少?
在金融的广阔舞台上,借款人的“信用基石”——即其综合资质,是决定贷款利率高低的决定性因素。这并非偶然,而是银行基于详尽的风险评估与收益预期所做出的精准判断。 需明确的是,贷款的易得性并不意味着无门槛的放任。它更像是设置…...

苹果电脑需要安装杀毒软件吗?探索Mac的安全世界!
在聊到电脑安全时,许多Mac用户都骄傲地声称:“我的Mac是不会中病毒的!”确实,与Windows PC相比,Mac因其UNIX-based的操作系统构架,天生就更加安全。但这是否意味着Mac完全不需要杀毒软件呢?让我…...

Oracle start with connect BY 死循环
解决办法 检查start with前有没有where条件, 如果有的话,套一层select,再 Oracle start with connect BY...

力扣接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表…...

bug“医典”
温馨提示:本篇文章主要用于收藏博主所遇到的各种bug,并且不定期更新 目录 未初始化 “病状” “处方” 数组越界 “病状” “处方” 未创建对象 “病状” 编辑 “处方” 未初始化 “病状” 这种是处在链表中的一种情况,通常是没有处理哨兵位…...

Track 06:量子计算机概述
量子计算机概述 量子计算机是基于量子力学原理的一种计算机,它与传统的经典计算机在处理信息的方式上有根本性的区别。量子计算机的设计和实现依赖于量子比特(qubits)和量子计算的核心概念,如叠加态和纠缠态,这些特性使其在解决某些复杂问题时具备传统计算机无法比拟的优…...

论文解读 | KDD2024 演化图上的森林矩阵快速计算
点击蓝字 关注我们 AI TIME欢迎每一位AI爱好者的加入! 点击 阅读原文 观看作者直播讲解回放! 作者简介 孙浩鑫,复旦大学博士生,主要研究方向为大规模图上快速算法设计。 概述 森林矩阵在网络科学、观点动力学和机器学习相关应用中…...
7.统一网关-Gateway
文章目录 1.统一网关介绍2.网关开发3.predicate4.Route Predicate Factories(路由断言工厂)4.1Path 路由断言工厂4.2.Method 路由断言工厂4.3 Header 路由断言工厂4.4 Query 路由断言工厂4.5 Host 路由断言工厂4.6 After 路由断言工厂4.7 Before 路由断言工厂4.8 Between 路由断…...

QT:QWidget 控件属性的介绍
控件属性介绍 🌴enabled 状态属性🌴geometry 几何属性示例一:改变控件尺寸示例二:更变控件位置window frame 的影响 🌴windowTitle 窗口标题🌴windowIcon 窗口图标🌴 qrc机制🌴windo…...

ctfshow-nodejs
什么是nodejs Node.js 是一个基于 Chrome V8 引擎的 Javascript 运行环境。可以说nodejs是一个运行环境,或者说是一个 JS 语言解释器 Nodejs 是基于 Chrome 的 V8 引擎开发的一个 C 程序,目的是提供一个 JS 的运行环境。最早 Nodejs 主要是安装在服务器…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...
