实验记录 | 点云处理 | K-NN算法3种实现的性能比较
引言
K近邻(K-Nearest Neighbors, KNN)算法作为一种经典的无监督学习算法,在点云处理中的应用尤为广泛。它通过计算点与点之间的距离来寻找数据点的邻居,从而有效进行点云分类、聚类和特征提取。本菜在复现点云文章过程,遇到了三种 KNN 的实现方式,故在此一并对比总结,最后对三种实现方案进行了性能比较。
在本文中,我将K近邻(KNN)算法的应用分为两种情况:
-
全局查询:对整个点云的所有 N 个点进行查询,找到每个点的 K 个最近邻点,最终返回的结果维度为 [B, N, K],B 表示批次大小,N 表示点的总数量,K 表示每个点的邻近点数量。
-
局部查询:针对已知的 S 个查询点,在整个点云的 N 个点中寻找每个查询点的 K 个最近邻点,最终返回的结果维度为 [B, S, K],其中 S 表示查询点的数量。
全局查询
def knn(x, k):"""Input:x: all points, [B, C, N]k: k nearest points of each pointReturn:idx: grouped points index, [B, N, k]"""inner = -2*torch.matmul(x.transpose(2, 1), x)xx = torch.sum(x**2, dim=1, keepdim=True)pairwise_distance = -xx - inner - xx.transpose(2, 1)idx = pairwise_distance.topk(k=k, dim=-1)[1] # (batch_size, num_points, k)return idx这段代码来源于点云网络的高引之作《Dynamic Graph CNN for Learning on Point Clouds》,实现了一个 KNN(K近邻)查询,目的是计算点云中每个点的 k 个最近邻点的索引。
函数清晰易懂,便不赘述。我一直以为点云学习是需要先采样,再用采样得到的中心点进行 KNN 邻域查询,直到看到这篇 DGCNN 的方法,才打破了我的固有认知:DGCNN没有下采样过程,直接使用 N 个点进行近邻查询和特征更新。
插个题外话,这篇文章真的值得一读,简单高效!不愧是高引之作。
局部查询
(1)knn_point 函数
def square_distance(src, dst):"""Calculate Euclid distance between each two points.src^T * dst = xn * xm + yn * ym + zn * zm;sum(src^2, dim=-1) = xn*xn + yn*yn + zn*zn;sum(dst^2, dim=-1) = xm*xm + ym*ym + zm*zm;dist = (xn - xm)^2 + (yn - ym)^2 + (zn - zm)^2= sum(src**2,dim=-1)+sum(dst**2,dim=-1)-2*src^T*dstInput:src: source points, [B, N, C]dst: target points, [B, M, C]Output:dist: per-point square distance, [B, N, M]"""B, N, _ = src.shape_, M, _ = dst.shapedist = -2 * torch.matmul(src, dst.permute(0, 2, 1))dist += torch.sum(src ** 2, -1).view(B, N, 1)dist += torch.sum(dst ** 2, -1).view(B, 1, M)return distdef knn_point(nsample, xyz, new_xyz):"""Input:nsample: max sample number in local regionxyz: all points, [B, N, C]new_xyz: query points, [B, S, C]Return:group_idx: grouped points index, [B, S, nsample]"""sqrdists = square_distance(new_xyz, xyz)_, group_idx = torch.topk(sqrdists, nsample, dim=-1, largest=False, sorted=False)return group_idx这段代码来源于另一个高引之作《Rethinking Network Design and Local Geometry in Point Cloud: A Simple Residual MLP Framework》,代码也是相当眉清目秀,不再赘述。其实这份代码的实现还是比较经典的,很多的模型代码都可以看到它的身影。
(2)knn_cuda 库函数
import torch# Make sure your CUDA is available.
assert torch.cuda.is_available()from knn_cuda import KNN
"""
if transpose_mode is True, ref is Tensor [bs x nr x dim]query is Tensor [bs x nq x dim]return dist is Tensor [bs x nq x k]indx is Tensor [bs x nq x k]
elseref is Tensor [bs x dim x nr]query is Tensor [bs x dim x nq]return dist is Tensor [bs x k x nq]indx is Tensor [bs x k x nq]
"""knn = KNN(k=10, transpose_mode=True)ref = torch.rand(32, 1000, 5).cuda()
query = torch.rand(32, 50, 5).cuda()dist, indx = knn(ref, query) # 32 x 50 x 10大佬把 KNN 封装为了库函数,来源于 KNN_CUDA 此仓库,可以参考 readme 进行安装。库函数的调用也非常方便。
需要强调的是,这里提到的 knn_point 和 knn_cuda 虽然算局部查询,但其实只要将局部查询点云 [B, S, Dim] 换成全局点云 [B, N, Dim] 作为输入,也就是全局查询了。
性能比较
(1)测试代码
import torch
import time
from knn_cuda import KNNdef knn(x, k):inner = -2*torch.matmul(x.transpose(2, 1), x)xx = torch.sum(x**2, dim=1, keepdim=True)pairwise_distance = -xx - inner - xx.transpose(2, 1)idx = pairwise_distance.topk(k=k, dim=-1)[1] # (batch_size, num_points, k)return idxdef square_distance(src, dst):B, N, _ = src.shape_, M, _ = dst.shapedist = -2 * torch.matmul(src, dst.permute(0, 2, 1))dist += torch.sum(src ** 2, -1).view(B, N, 1)dist += torch.sum(dst ** 2, -1).view(B, 1, M)return distdef knn_point(nsample, xyz, new_xyz):sqrdists = square_distance(new_xyz, xyz)_, group_idx = torch.topk(sqrdists, nsample, dim=-1, largest=False, sorted=False)return group_idx# Custom knn implementation
def test_knn(query, k, times):query = query.permute(0,2,1)start_time = time.time() # Start timerfor i in range(times):indx = knn(query, k = k)end_time = time.time() # End timerreturn end_time - start_time # Return elapsed time# Custom knn_point implementation
def test_knn_point(ref, query, k, times):start_time = time.time() # Start timerfor i in range(times):indx = knn_point(k, ref, query)end_time = time.time() # End timerreturn end_time - start_time # Return elapsed time# knn_cuda implementation
def test_knn_cuda(ref, query, k, times):knn = KNN(k=k, transpose_mode=True)start_time = time.time() # Start timerfor i in range(times):dist, indx = knn(ref, query)end_time = time.time() # End timerreturn end_time - start_time # Return elapsed time# Main testing function
def test_knn_methods(ref, query, k, times):print("Test times: %d" % times)# Test custom knntime_knn = test_knn(query, k, times)print(f"knn : {time_knn:.6f} seconds")# Test custom knn_pointtime_point = test_knn_point(ref, query, k, times)print(f"knn_point: {time_point:.6f} seconds")# Test knn_cudatime_cuda = test_knn_cuda(ref, query, k, times)print(f"knn_cuda : {time_cuda:.6f} seconds")if __name__ == '__main__':# Sample inputB, N, S, C = 32, 1024, 50, 3 # Batch size, total points, query points, coordinatesk = 24 # Number of nearest neighborsref = torch.randn(B, N, C).cuda() # Reference points# Test above methodstimes_list = [1,2,3,10,50,100]for times in times_list:test_knn_methods(ref, ref, k, times)这段代码测试了三种 K 近邻(KNN)算法的实现效率,分别是自定义的 knn、knn_point 以及基于 knn_cuda 库的实现。分别对每种方法运行多次,记录每种方法在不同重复次数(如 1、2、3、10、50、100 次)的运行时间,最终输出各方法的执行时间。

上图展示了测试代码的结果,可以看到 knn_cuda 的实现方式表现最差的(我也表示非常不理解);knn 和 knn_point 性能表现相当。或许这也是为什么很多较新的模型使用的也是 knn_point,而不是 knn_cuda。
当然,这份测试代码实际是在一个小规模数据的单卡上进行的,或许无法很好地展现出他们在实际训练的性能,因此我又分别将他们部署在 DGCNN 模型上进行训练,对比性能。
(2)模型训练



直接将他们部署在模型的训练中,能够最真实反映出他们的性能。这次实验,Batchsize 设置为了32,epoch 设置为256,选择前2个epoch观察。从训练状态可以看到,红色框选区域表示训练和测试的时间,knn_cuda 依然稳定发挥,表现最差哈哈哈哈,knn 和 knn_point 的函数实现表现相当。
总结
我原以为 knn_cuda 会很厉害,毕竟是直接封装起来了,但实际表现不尽人意。看似很小的性能差异,放在规模较大的数据集上,训练成本可是指数级倍增的。所以,还是尽可能使用 knn 和 knn_point 来实现全局/局部的邻近查询。
相关文章:

实验记录 | 点云处理 | K-NN算法3种实现的性能比较
引言 K近邻(K-Nearest Neighbors, KNN)算法作为一种经典的无监督学习算法,在点云处理中的应用尤为广泛。它通过计算点与点之间的距离来寻找数据点的邻居,从而有效进行点云分类、聚类和特征提取。本菜在复现点云文章过程ÿ…...

【OJ】常用技巧
1. 模版 #include<bits/stdc.h> using namespace std;int main(){ios::sync_with_stdio(false);cin.tie(0);// write herereturn 0; }2. 填充数组 memset是一个字节一个字节填充,如果是使int类型填充非0或者-1就会报错,如 int a[100]; memset(a…...

Redis:Redis性能变慢的原因
一、淘汰策略性能问题 当使用Redis当作缓存使用时,通常会给这个实例设置内存上限maxmemory,然后设置一个数据淘汰策略;如果Redis实例设置了内存上限maxmemory,那么也有可能导致Redis变慢。 原因在于,当Redis内存达到…...

Linux多线程——利用C++模板对pthread线程库封装
文章目录 线程封装主要框架线程启动线程等待其他信息 测试函数 线程封装 我们之前介绍过pthread的线程库,这个线程库主要是基于C语言的void*指针来进行传参和返回 我们使用C的模板对其封装可以让他的使用更加方便,并且经过测试可以让我们更加直观的了解…...

SpringBoot教程(十五) | SpringBoot集成RabbitMq(消息丢失、消息重复、消息顺序、消息顺序)
SpringBoot教程(十五) | SpringBoot集成RabbitMq(消息丢失、消息重复、消息顺序、消息顺序) RabbitMQ常见问题解决方案问题一:消息丢失的解决方案(1)生成者丢失消息丢失的情景解决方案1…...

TensorRT-LLM高级用法
--multi_block_mode decoding phase, 推理1个新token, 平时:按照batch样本,按照head,将计算平均分给所有SM; batch_size*num_heads和SM数目相比较小时:有些SM会空闲;加了--multi_block_mode&…...
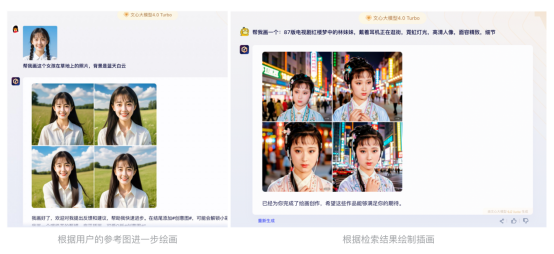
文心一言功能新升级:读文档、懂翻译、能识图
9月4日,百度文心一言官网显示,在向全社会开放一周年之际,文心一言进行了功能最新全面升级,同时在周年期间为新老会员增加1个月专业版免费使用体验。 据了解,针对网页版用户需求,文心一言实现了创作内容更加…...

C++机试——走方格的方案
题目 请计算n*m的棋盘格子(n为横向的格子数,m为竖向的格子数)从棋盘左上角出发沿着边缘线从左上角走到右下角,总共有多少种走法,要求不能走回头路,即:只能往右和往下走,不能往左和往…...

Bootstrap 字体图标无法显示问题,<i>标签字体图标无法显示问题
bootstrap fileInput 以及 Bootstrap 字体图标无法显示问题。 今天在用 bootstrap fileInput 插件的时候发现图标无法显示,如下: 查看DOM,发现那些图标是<i>标签做的: 网上的方案 方案1 网上很多人说是我们打乱了boots…...

docker registry 仓库加密
docker registry 仓库加密 1、背景 公司一直用的镜像仓库是docker registry,但是有个安全问题,就是仓库从web ui的浏览到镜像的拉取都是可以直接使用的,还是放到了公网上,只需要知道你的域名那就是畅通无阻了,可以…...

利用高德+ArcGIS优雅获取任何感兴趣的矢量边界
荷花十里,清风鉴水,明月天衣。 四时之景不同,乐亦无穷尽也。今天呢,梧桐君给大家讲解一下,如何利用高德地图,随机所欲的获取shp边界数据。 文章主要分成以下几个步骤: 首先搜索你想获取的矢量…...

炮弹【USACO】
题目背景 时/空限制:1s / 64MB 题目描述 贝茜已经精通了变成炮弹并沿着长度为 N 的数轴弹跳的艺术,数轴上的位置从左到右编号为 1,2,…,N 。 她从某个整数位置 S 开始,以 1 的起始能量向右弹跳。 如果贝茜的能量为 k ,则她将…...

python如何读取excel文件内的数据
目录 前言一、安装openpyxl二、读取Excel数据总结前言 在Python中读取Excel数据,最常用的库之一是openpyxl(用于.xlsx格式)和xlrd(尽管xlrd从版本2.0开始不再支持.xlsx,仅支持旧的.xls格式)。然而,对于大多数现代应用来说,openpyxl是一个更好的选择,因为它支持.xlsx格…...

Java项目: 基于SpringBoot+mybatis+maven+mysql教师工作量管理系统(含源码+数据库+毕业论文)
一、项目简介 本项目是一套基于SpringBootmybatismavenmysql教师工作量管理系统 包含:项目源码、数据库脚本等,该项目附带全部源码可作为毕设使用。 项目都经过严格调试,eclipse或者idea 确保可以运行! 该系统功能完善、界面美观…...

项目开发--数据库--postgresql数据库操作
背景 1、安装postgresql的基础方法 2、基本操作命令 解决方案 安装命令 在ubuntu环境当中进行安装。 sudo apt install postgresql安装完毕之后直接进行测试,如果看到如下内容则安装成功。 sudo systemctl status postgresql使用DBeaver进行连接报错ÿ…...

c语言——用一维数组输出杨辉三角形
一.代码 #include <stdio.h> int Num[100]; int Hang; int Lie; int a; int Flag; int main() {Lie 1;Hang 1;a 0;while (1) {//列1为1if (Lie 1) {Num[1] 1;Lie;}//数据存到数组里面while (Hang > Lie && Hang ! 2) { if (Hang!Lie) {Flag Num[Lie] …...
 (A~G1))
Codeforces Round 971 (Div. 4) (A~G1)
A、B题太简单,不做解释 C 对于 x y 两个方向,每一个方向至少需要 x / k 向上取整的步数,取最大值。 由于 x 方向先移动,假如 x 方向需要的步数多于 y 方向的步数,那么最后 y 方向的那一步就不需要了,答案…...

为什么构造函数不能为虚函数?为什么析构函数可以为虚函数,如果不设为虚函数可能会存在什么问题?
目录 一、为什么构造函数不能为虚函数? 二、为什么析构函数可以是虚函数?如果不设为虚函数可能会存在什么问题? 构造函数不能为虚函数,因为在构造过程中,虚函数机制尚未生效,对象还未完成构造,…...

【数据结构】单链表功能的实现
目录 1.链表的概念及结构 2.单链表功能的实现 2.1打印单链表 2.2创建节点 2.3单链表尾插 2.3单链表头插 2.5单链表尾删 2.6单链表头删 2.7单链表的查找 2.8在指定位置之前插入数据 2.9在指定位置之后插入数据 2.10删除pos节点 2.11删除pos之后的节点 2.12销毁链表…...

最新车型库大全|阿里云实现调用API接口
整体请求流程: 介绍: 本次解析通过阿里云云市场的云服务来实现查询车型库大全查询,首先需要选择一家可以提供查询的商品。 [探数API]车型库查询_API专区_云市场-阿里云 步骤1: 选择商品 如图点击免费试用,即可免费申请该接口数…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...
