Codeforces Round 971 (Div. 4) (A~G1)

A、B题太简单，不做解释

C

对于 x y 两个方向，每一个方向至少需要 x / k 向上取整的步数，取最大值。
由于 x 方向先移动，假如 x 方向需要的步数多于 y 方向的步数，那么最后 y 方向的那一步就不需要了，答案减 1

代码

#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <cmath>
using namespace std;
using LL = long long;void slove()
{int x, y, k; cin >> x >> y >> k;int h = ceil((double)y / k);int l = ceil((double)x / k);int res = max(h, l);res *= 2;if (l > h) res--;cout << res << endl;
} int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int t = 1; cin >> t;while (t--) slove();return 0;
}

D

注意到 y 的范围为: [0, 1]，当两点连线垂直 x 轴时，与其余任意点都可以组成直角形。
还有一种组成直角三角形的情况是：一条水平线的点和另一条水平线的两个点组成直角三角形，单独的点的 x 轴坐标位于两点中间，且距离两点长度为 1（由等腰直角三角形的性质可得）

代码

#include <iostream>
#include <algorithm>
#include <vector>
#include <cstring>
#include <string>
#include <cmath>
#include <map>
using namespace std;
using LL = long long;void slove()
{int n; cin >> n;vector<vector<int>> a(n + 5, vector<int>(2));for (int i = 0; i < n; i++){int x, y; cin >> x >> y;a[x][y]++;}LL res = 0;for (int i = 0; i <= n; i++){res += (LL) a[i][0] * a[i][1] * (n - 2);if (i == 0 || i == n) continue;res += (LL) a[i - 1][0] * a[i][1] * a[i + 1][0];res += (LL) a[i - 1][1] * a[i][0] * a[i + 1][1];}cout << res << endl;
}  int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int t = 1; cin >> t;while (t--) slove();return 0;
}

E

注意到数列是一个公差为 1 的等差数列，首项为 k，那么可以根据等差数列的求和公式得到前 i 项的和，i 的范围为: [1, n]
为了使得前缀和后缀差值最小，可以二分 i 的位置，得到最后一个前缀和 小于等于 后缀和的位置；差值需要取该位置的差值和后一个位置的最小值。

#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <cmath>
#include <map>
using namespace std;
using LL = long long;
typedef pair<int, int> PII;void slove()
{LL n, k; cin >> n >> k;LL t = (LL) n * (2 * k + n - 1) / 2;int l = 1, r = n + 1;while (l < r){int mid = l + r  + 1 >> 1;LL pre = (LL) mid * (2 * k + mid - 1) / 2;LL suf = t - pre;if (pre <= suf) l = mid;else r = mid - 1;}LL res = 1e18;LL pre = (LL) l * (2 * k + l - 1) / 2;LL suf = t - pre;// cout << abs(pre - suf) << endl;res = min(res, abs(pre - suf));l++;pre = (LL) l * (2 * k + l - 1) / 2;suf = t - pre;res = min(res, abs(pre - suf));// cout << abs(pre - suf) << endl;cout << res << endl;
} int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int t = 1; cin >> t;while (t--) slove();return 0;
}

F

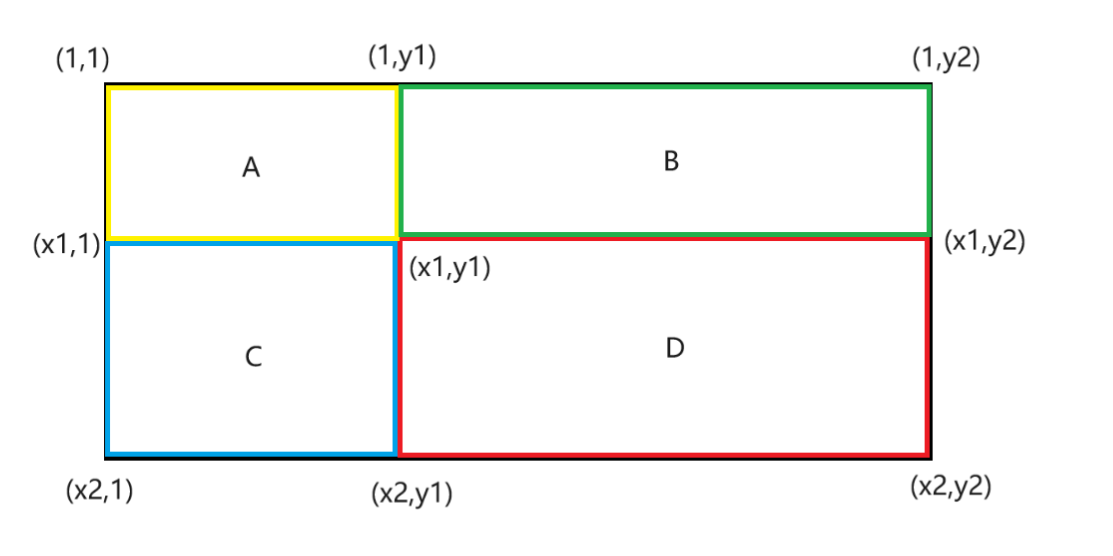
数组 b 可以理解为由数组 a 组成的 n x n 的二维矩阵，第 i 行由 ai....an a1...ai-1 组成。
对于每一个询问 l，r；可以将 l，r 映射到由两个 a 数组组成的新的数组中。
对于 l 到 r 的和，可以使用前缀和。首先可以计算出 l 和 r 位于 b 的第几层，假如不是位于同一层，那么中间的层数的和是由 a 的和组成的。然后就是处理 l 到该层末尾的和，r 到层首的和。

#include <iostream>
#include <cmath>
#include <vector>
#include <algorithm>
using namespace std;
using LL = long long;LL get_pre(vector<LL>& pre, LL cen, LL x)
{int start = x + cen;return pre[start] - pre[cen - 1];
}void slove()
{int n, q; cin >> n >> q;vector<LL> nums(2 * n + 10);vector<LL> pre(2 * n + 10);for (int i = 1; i <= n; i++){cin >> nums[i];nums[i + n] = nums[i];}for (int i = 1; i <= 2 * n; i++){pre[i] = pre[i - 1] + nums[i];}while (q--){LL l, r; cin >> l >> r;LL cen_l = ceil(1.0 * l / n);LL cen_r = ceil(1.0 * r / n);// cout << cen_l << " " << cen_r << endl;int cnt = cen_r - cen_l - 1;LL res = (LL) max(0, cnt) * pre[n];// cout << res << endl;l--, r--;l %= n, r %= n;// cout << l << " " << r << endl;if (cen_l == cen_r){res += get_pre(pre, cen_l, r) - get_pre(pre, cen_l, l - 1);// cout << nums[cen_l + l] <<  endl;}else{res += pre[n] - get_pre(pre, cen_l, l - 1) + get_pre(pre, cen_r, r);}cout << res << endl;}}int main()
{int t; cin >> t;while (t--) slove();return 0;
}

G1

可以将数组的元素 - i，这样对于两个元素如果是连续的子数组的话，那么值就会相同。
证明如下：
对于任意两哥元素 ai aj，另 j - i = k，那么假如 ai 和 aj 满足连续子数组的要求得话，有 aj = ai + k,
ai - i，aj - j = ai + k - j = ai + j - i -j = ai - i。所以当两个元素满足连续子数组的要求，那么减下标将会相等。

对于一个区间需要改变的最小次数等于 len - maxv。（len 表示区间元素个数，maxv 表示区间内满足连续子数组要求的最大元素个数）问题就转变为求区间内最长连续子数组的元素个数。

使用 map 存储每一个元素减下标的个数，使用 multiset 存储个数。对于区间长度 k，可以使用滑动窗口预处理从每一个下标开始，窗口长度为 k 的最大相同元素个数。
先枚举 [1, k)，维护出第一个滑动窗口中相等元素个数。然后依次向后移动，增加进入的元素，减去出去的元素。注意：每枚举一个元素，都会向 multiset 中插入个数，但是在插入之前会将该元素对应的值的个数在 multiset 中减去，否则就重复加了。在这里就需要注意 multiset 的用法：在 erase 之前需要保证 multiset 中有这个值，所以可以在操作之前，先插入 n 个 0，不会影响到答案的获取。

代码

#include <iostream>
#include <cmath>
#include <vector>
#include <algorithm>
#include <map>
#include <set>
using namespace std;
using LL = long long;void slove()
{int n, k, q; cin >> n >> k >> q;vector<int> nums(n + 10);vector<int> res (n + 10);for (int i = 1; i <= n; i++) cin >> nums[i];map<int, int> mp;multiset<int> s;for (int i = 1; i <= n; i++) s.insert(0);  // 由于需要先删除，当一个元素没有进入过multiset之前就会为0，那么for (int i = 1; i < k; i++)  // 先处理好第一个窗口{s.erase(s.find(mp[nums[i] - i]));  // 在增加这个个数之前，需要先删除这个个数之前的插入，这样就可以保证不会重复。mp[nums[i] - i]++;s.insert(mp[nums[i] - i]);  // 增加个数到 multiset 中}for (int i = k; i <= n; i++){s.erase(s.find(mp[nums[i] - i]));mp[nums[i] - i]++;s.insert(mp[nums[i] - i]);int p = i - k + 1;res[p] = *s.rbegin();s.erase(s.find(mp[nums[p] - p]));mp[nums[p] - p]--;s.insert(mp[nums[p] - p]);}while (q--){int l, r; cin >> l >> r;cout << k - res[l] << endl;}
}int main()
{int t; cin >> t;while (t--) slove();return 0;
}