如何修复软件中的BUG
笔者上一篇博文《如何开发出一款优秀的软件》主要讲了如何开发一款优秀的软件及相应的必要条件。但对一个已上线,已经成型的产品,该如何解决存在的bug呢?这是本文要阐述的内容。
在这里,首先说一下bug的种类及bug严重程度分类,请看下面的图一与图二:


如上图,分别为bug的种类及bug严重程度分类,通常遇到bug,都是按bug严重程度分类,比如我们用到的jira和禅道管理软件,按优先级依次解决致命bug、严重bug……而把一般bug、轻微bug放后。通常这样的做法也没有问题,但笔者认为软件是一个整体,如果粗略的这样分,可能会混淆我们的思路,不利于我们解决问题。我们不应该因为bug属于Medium而忽视它,说不定一个小的Medium可能后面隐藏着影响全局的大文章。我们就要静下心来,好好考虑一下。在这里笔者建议按bug类型来将bug进行归类,全方位的分析一下所有的bug。那么接下来,笔者就述说一下,如何正确解决软件中的bug问题,步骤如下:
第一:将所有bug统计在一起,并进行归类,按图一中的方法进行分类。即按功能类、功能缺陷类、性能类等11大类(可根据实际情况,增加分类)进行分类。
第二:梳理整体软件架构,并标识出bug所在位置。软件架构包括前端架构,后端架构、数据库部署架构,消息中间件部署架构,缓存架构、负载均衡架构等。
第三:分析软件架构。分析软件设计架构,部署架构,看是否合理;针对标准规范类bug,看框架设计是否遵循了行业标准协议,或者自定义的协议是否规范;对于设计缺陷类bug,查看设计中的不合理的地方;对于安装部署类bug,要详细看看相应软件的部署环境,操作系统,中间件等版本及功能支持情况;对于配置相关类bug,要仔细检查部署及配置情况,找出疏漏;对安全类bug,要从安全设计方案里排查解决及安全框架及代码编写;对兼容性类bug,要从设计及代码级别审查,比如如果用到了适配器设计模式,那么这种设计是否考虑周全等等;对于性能类bug,需要全面分析设计架构及部署架构,包括但不限于数据库表结构设计,负载均衡设计、异步设计及各种中间件设计等;对于功能缺陷类bug,查看设计方案,是否属于设计时漏选,还是编写代码时没有实现相应功能,必要时还需要查看需求文档等;对于功能类bug,也需要检查设计方案是否合理,业务逻辑是否合理,部署方案是否合理;功能不稳定,是否存在大模块问题,及业务模块拆分不合理,相同功能模块没有拆分出来公用,设计及编码冗余,是否存在业务模块设计,软件架构设计不合理问题,关于这点说明,请参见《如何开发出一款优秀的软件》中相应内容的论述。
以上是笔者关于解决软件bug问题的三步方法,其实解决软件bug的方法最重要的是规范开发软件,避免或者减少bug的产生,关于这点请参见《如何开发出一款优秀的软件》中相应内容的论述。
相关文章:

如何修复软件中的BUG
笔者上一篇博文《如何开发出一款优秀的软件》主要讲了如何开发一款优秀的软件及相应的必要条件。但对一个已上线,已经成型的产品,该如何解决存在的bug呢?这是本文要阐述的内容。 在这里,首先说一下bug的种类及bug严重程度分类&…...

分享一个基于微信小程序的医院挂号就诊一体化平台uniapp医院辅助挂号应用小程序设计(源码、调试、LW、开题、PPT)
💕💕作者:计算机源码社 💕💕个人简介:本人 八年开发经验,擅长Java、Python、PHP、.NET、Node.js、Android、微信小程序、爬虫、大数据、机器学习等,大家有这一块的问题可以一起交流&…...

HTML生日蛋糕
目录 写在前面 完整代码 代码分析 系列文章 写在最后 写在前面 HTML实现的生日蛋糕来喽,小编亲测,发给好友可以直接打开哦。在代码的第183行可以写下对朋友的祝福,快拿去送给你的好朋友吧! 完整代码 <!DOCTYPE html>…...
寄存器寻址,每天5分钟学习逆向吧!)
【软件逆向】第27课,软件逆向安全工程师之(二)寄存器寻址,每天5分钟学习逆向吧!
寄存器寻址是汇编语言中的一种寻址方式,在这种方式中,操作数位于CPU的寄存器中。寄存器是CPU内部的高速存储位置,用于快速访问数据。以下是关于寄存器寻址的详细信息: 寄存器寻址的特点: 操作数在寄存器中࿱…...

前缀和 — 利用前缀信息解决子数组问题
【前缀和的核心思想是预先处理数组来快速计算任意子数组的和,基本上用于数组和序列问题。】 前缀和算法具体步骤 构造前缀和数组: 给定一个数组nums,其前缀和数组prex定义为prex[i]表示为数组nums从起始位置到第i个位置的元素累加和。构建前…...
2024年最新版Ajax+Axios 学习【包含原理、Promise、报文、接口等...】
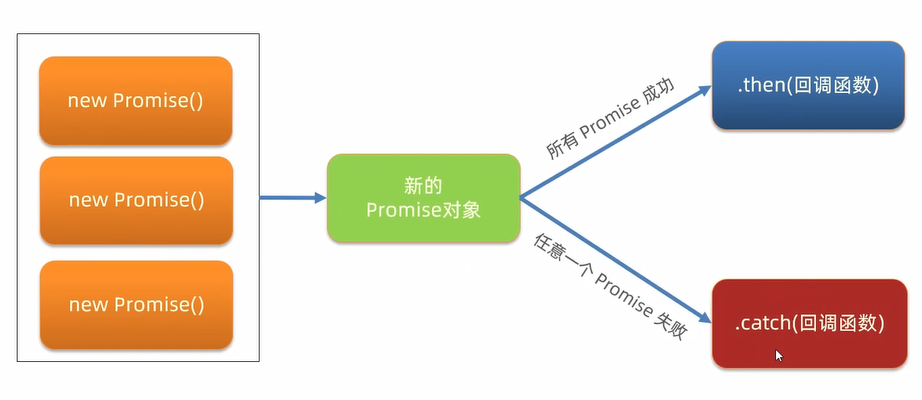
基础知识 AJAX概念 AJAX概念:是浏览器与服务器进行数据通信的技术。 认识URL 定义:统一资源定位符,简称网址,用于访问网络上的资源。 组成: http协议:超文本传输协议,规定浏览器和服务器之…...

【Qt线程】—— Qt线程详解
目录 (一)多线程的概述 (二)Qt线程的使用条件 (三)创建线程的方法 3.1 继承QTread,重写run()函数 3.1.1 为什么要重写 3.2 继承QObject 3.3 核心API介绍 3.4 关闭线程的使用方法 &…...

Golang | Leetcode Golang题解之第391题完美矩形
题目: 题解: func isRectangleCover(rectangles [][]int) bool {type point struct{ x, y int }area, minX, minY, maxX, maxY : 0, rectangles[0][0], rectangles[0][1], rectangles[0][2], rectangles[0][3]cnt : map[point]int{}for _, rect : range…...

〖open-mmlab: MMDetection〗解析文件:mmdet/models/detectors/two_stage.py
目录 MMDetection中的两阶段检测器:深入解析two_stage.py源码两阶段检测器概述two_stage.py的关键组件类定义和初始化构造函数Neck头配置RPN头配置RoI头配置_load_from_state_dict方法概述参数解释代码解析 特征提取方法签名文档字符串(Docstring&#x…...

【最新华为OD机试E卷-支持在线评测】机器人活动区域(100分)多语言题解-(Python/C/JavaScript/Java/Cpp)
🍭 大家好这里是春秋招笔试突围 ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-E/D卷的三语言AC题解 💻 ACM金牌🏅️团队| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 🍿 最新华为OD机试D卷目录,全、新、准,题目覆盖率达 95% 以上,…...

C语言:刷题日志(1)
一.阶乘计算升级版 本题要求实现一个打印非负整数阶乘的函数。 其中n是用户传入的参数,其值不超过1000。如果n是非负整数,则该函数必须在一行中打印出n!的值,否则打印“Invalid input”。 首先,知道阶乘是所有小于及等于该数的…...
导入失败,Windows OpenSSl 1.1.1 下载)
ios私钥证书(p12)导入失败,Windows OpenSSl 1.1.1 下载
ios私钥证书(p12)导入失败 如果你用的OpenSSL版本是v3那么恭喜你V3必然报这个错,解决办法将OpenSSL 3降低成 v1。 Windows OpenSSl 1.1.1 下载 阿里云网盘下载地址:OpenSSL V1...

嵌入式面试经典30问:二
1. 嵌入式系统中,如何选择合适的微控制器或微处理器? 在嵌入式系统中选择合适的微控制器(MCU)或微处理器(MPU)时,需要考虑多个因素以确保所选组件能够满足项目的具体需求。以下是一些关键步骤和…...

目标检测-YOLOv1
YOLOv1介绍 YOLOv1(You Only Look Once version 1)是一种用于目标检测的深度学习算法,由Joseph Redmon等人于2016年提出。它基于单个卷积神经网络,将目标检测任务转化为一个回归问题,通过在图像上划分网格并预测每个网…...

python基础语法八-异常
书接上回: python基础语法一-基本数据类型 python基础语法二-多维数据类型 python基础语法三-类 python基础语法四-数据可视化 python基础语法五-函数 python基础语法六-正则匹配 python基础语法七-openpyxl操作excel 1. 异常简介 (1)异常:遇到…...

【堆的应用--C语言版】
前面一节我们都已将堆的结构(顺序存储)已经实现,对树的相关概念以及知识做了一定的了解。其中我们在实现删除操作和插入操作的时候,我们还同时实现了建大堆(小堆)的向上(下)调整算法…...

【微信小程序】搭建项目步骤 + 引入Tdesign UI
目录 创建1个空文件夹,选择下图基础模板 开启/支持sass 创建公共style文件并引入 引入Tdesign UI: 1. 初始化: 2. 安装后,开发工具进行构建: 3. 修改 app.json 4. 使用 5. 自定义主题色 创建1个空文件夹,选择下…...

android系统源码12 修改默认桌面壁纸--SRO方式
1、aosp12修改默认桌面壁纸 代码路径 :frameworks\base\core\res\res\drawable-nodpi 替换成自己的图片即可,不过需要覆盖所有目录下的图片。 由于是静态修改,则需要make一下,重新编译。 2、方法二Overlay方式 由于上述方法有…...

Echarts可视化
echarts是一个基于javascripts的开源可视化图表库 画图步骤: 1.引入echarts.js文件 <script src" https://cdn.jsdelivr.net/npm/echarts5.5.1/dist/echarts.min.js"></script> 也可将文件下载到本地通过src引入。 2. 准备一个呈现图表的…...

验证linux gpu是否可用
通过torch验证 import torchprint(torch.__version__) # 查看torch当前版本号 print(torch.version.cuda) # 编译当前版本的torch使用的cuda版本号 print(torch.cuda.is_available()) # 查看当前cuda是否可用于当前版本的Torch,如果输出True,则表示可…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
