力扣9.7
115.不同的子序列
题目
给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 109 + 7 取模。
数据范围
1 <= s.length, t.length <= 1000s和t由英文字母组成
分析
令dp[i][j]为s的前i个字符构成的子序列中为t的前j个字符的数量,接下来设置边界条件,当t为空时s前i个字符构成子序列只要空字符串满足,个数为1,即dp[i][0]=1,考虑状态转移
- 当 s [ i ] ! = t [ j ] , d p [ i + 1 ] [ j + 1 ] = d p [ i ] [ j ] ; 当s[i]!=t[j],dp[i + 1][j + 1] = dp[i][j]; 当s[i]!=t[j],dp[i+1][j+1]=dp[i][j];
- 当 s [ i ] = = t [ j ] , d p [ i + 1 ] [ j + 1 ] = d p [ i ] [ j ] + d p [ i ] [ j + 1 ] ; 当s[i]==t[j],dp[i+1][j+1] = dp[i][j] + dp[i][j + 1]; 当s[i]==t[j],dp[i+1][j+1]=dp[i][j]+dp[i][j+1];
代码
class Solution {
public: const static int N = 1005, mod = 1e9 + 7;int dp[N][N];int numDistinct(string s, string t) {if(s.size() < t.size()) return 0;for(int i = 0; i < s.size(); i ++ ) dp[i][0] = 1;for(int i = 0; i < s.size(); i ++ ) {for(int j = 0; j <= i && j < t.size(); j ++ ) {if(s[i] != t[j]) dp[i + 1][j + 1] = dp[i][j + 1];else dp[i + 1][j + 1] += dp[i][j] + dp[i][j + 1];dp[i + 1][j + 1] %= mod;}} return dp[s.size()][t.size()];}
};
63.不同路径Ⅱ
题目
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
数据范围
m == obstacleGrid.lengthn == obstacleGrid[i].length1 <= m, n <= 100obstacleGrid[i][j] 为 0 或 1
分析
令dp[i][j]为到那个格子的路径数,考虑状态转移
- 如果有障碍物, d p [ i ] [ j ] = 0 dp[i][j]=0 dp[i][j]=0
- 没有障碍物, d p [ i ] [ j ] = d p [ i − 1 ] [ j ] + d p [ i ] [ j − 1 ] dp[i][j]=dp[i-1][j]+dp[i][j-1] dp[i][j]=dp[i−1][j]+dp[i][j−1]
代码
class Solution {
public:const static int N = 105;int dp[N][N];int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int n = obstacleGrid.size(), m = obstacleGrid[0].size();for(int i = 0; i < n; i ++ ) {for(int j = 0; j < m; j ++ ) {if(!i && !j && !obstacleGrid[i][j]) {dp[i + 1][j + 1] = 1;continue;}if(obstacleGrid[i][j]) dp[i + 1][j + 1] = 0;else dp[i + 1][j + 1] = dp[i][j + 1] + dp[i + 1][j]; }}return dp[n][m];}
};
746.使用最小花费爬楼梯
题目
给你一个整数数组 cost ,其中cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
数据范围
2 <= cost.length <= 10000 <= cost[i] <= 999
分析
令dp[i]为到达那一层的最小花费,状态转移:
- d p [ i ] = m i n ( d p [ i − 1 ] + c o s t [ i − 1 ] , d p [ i − 2 ] + c o s t [ i − 2 ] ) dp[i]=min(dp[i-1]+cost[i - 1],dp[i-2] + cost[i - 2]) dp[i]=min(dp[i−1]+cost[i−1],dp[i−2]+cost[i−2])
代码
class Solution {
public:const static int N = 1005;int dp[N];int minCostClimbingStairs(vector<int>& cost) {dp[0] = dp[1] = 0;for(int i = 2; i <= cost.size(); i ++ ) {dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);}return dp[cost.size()];}
};
相关文章:

力扣9.7
115.不同的子序列 题目 给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 109 7 取模。 数据范围 1 < s.length, t.length < 1000s 和 t 由英文字母组成 分析 令dp[i][j]为s的前i个字符构成的子序列中为t的前j…...

GPU 带宽功耗优化
移动端GPU 的内存结构: 先简述移动端内存cache结构;上图的UMA结构 on-Chip memory 包括了 L1、L2 cache,非常关键的移动端的 Tiles 也是保存在 on-chip上还包括寄存器文件:提供给每个核心使用的极高速存储。 共享内存(…...

Linux Centos 7网络配置
本步骤基于Centos 7,使用的虚拟机是VMware Workstation Pro,最终可实现虚拟机与外网互通。如为其他发行版本的linux,可能会有差异。 1、检查外网访问状态 ping www.baidu.com 2、查看网卡配置信息 ip addr 3、配置网卡 cd /etc/sysconfig…...

第三天旅游线路规划
第三天:从贾登峪到禾木风景区,晚上住宿贾登峪; 从贾登峪到禾木风景区入口: 1、行程安排 根据上面的耗时情况,规划一天的行程安排如下: 1)早上9:00起床,吃完早饭&#…...

C++第四十七弹---深入理解异常机制:try, catch, throw全面解析
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】【C详解】 目录 1.C语言传统的处理错误的方式 2.C异常概念 3. 异常的使用 3.1 异常的抛出和捕获 3.2 异常的重新抛出 3.3 异常安全 3.4 异常规范 4.自定义…...

go 和 java 技术选型思考
背景: go和java我这边自身都在使用,感受比较深,java使用了有7年多,go也就是今年开始的,公司需要所以就学了使用,发现这两个语言都很好,需要根据场景选择,我写下我这边的看法。 关于…...

传统CV算法——边缘算子与图像金字塔算法介绍
边缘算子 图像梯度算子 - Sobel Sobel算子是一种用于边缘检测的图像梯度算子,它通过计算图像亮度的空间梯度来突出显示图像中的边缘。Sobel算子主要识别图像中亮度变化快的区域,这些区域通常对应于边缘。它是通过对图像进行水平和垂直方向的差分运算来…...

图像去噪算法性能比较与分析
在数字图像处理领域,去噪是一个重要且常见的任务。本文将介绍一种实验,通过MATLAB实现多种去噪算法,并比较它们的性能。实验中使用了包括中值滤波(MF)、自适应加权中值滤波(ACWMF)、差分同态算法…...
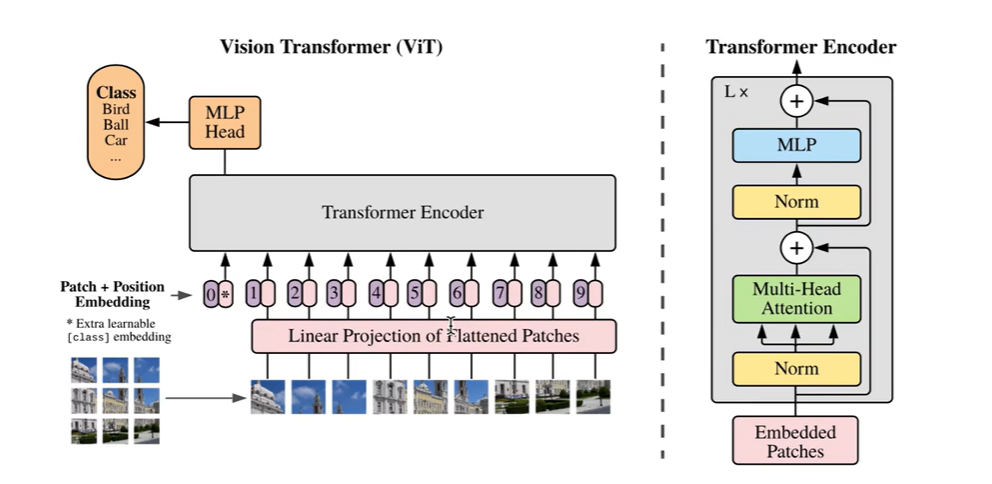
Vision Transformer(ViT)模型原理及PyTorch逐行实现
Vision Transformer(ViT)模型原理及PyTorch逐行实现 一、TRM模型结构 1.Encoder Position Embedding 注入位置信息Multi-head Self-attention 对各个位置的embedding融合(空间融合)LayerNorm & ResidualFeedforward Neural Network 对每个位置上单…...

828华为云征文 | Flexus X实例CPU、内存及磁盘性能实测与分析
引言 随着云计算的普及,企业对于云资源的需求日益增加,而选择一款性能强劲、稳定性高的云实例成为了关键。华为云Flexus X实例作为华为云最新推出的高性能实例,旨在为用户提供更强的计算能力和更高的网络带宽支持。最近华为云828 B2B企业节正…...
队列)
FreeRTOS学习笔记(六)队列
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、队列的基本内容1.1 队列的引入1.2 FreeRTOS 队列的功能与作用1.3 队列的结构体1.4 队列的使用流程 二、相关API详解2.1 xQueueCreate2.2 xQueueSend2.3 xQu…...

【Python篇】PyQt5 超详细教程——由入门到精通(中篇一)
文章目录 PyQt5入门级超详细教程前言第4部分:事件处理与信号槽机制4.1 什么是信号与槽?4.2 信号与槽的基本用法4.3 信号与槽的基础示例代码详解: 4.4 处理不同的信号代码详解: 4.5 自定义信号与槽代码详解: 4.6 信号槽…...

LinuxQt下的一些坑之一
我们在使用Qt开发时,经常会遇到Windows上应用正常,但到Linux嵌入式下就会出现莫名奇妙的问题。这篇文章就举例分析下: 1.QPushButton按钮外侧虚线框问题 Windows下QPushButton按钮设置样式正常,但到了Linux下就会有一个虚线边框。…...

Statement batch
我们可以看到 Statement 和 PreparedStatement 为我们提供的批次执行 sql 操作 JDBC 引入上述 batch 功能的主要目的,是加快对客户端SQL的执行和响应速度,并进而提高数据库整体并发度,而 jdbc batch 能够提高对客户端SQL的执行和响应速度,其…...

PPP 、PPPoE 浅析和配置示例
一、名词: PPP: Point to Point Protocol 点到点协议 LCP:Link Control Protocol 链路控制协议 NCP:Network Control Protocol 网络控制协议,对于上层协议的支持,N 可以为IPv4、IPv6…...

【Python机器学习】词向量推理——词向量
目录 面向向量的推理 使用词向量的更多原因 如何计算Word2vec表示 skip-gram方法 什么是softmax 神经网络如何学习向量表示 用线性代数检索词向量 连续词袋方法 skip-gram和CBOW:什么时候用哪种方法 word2vec计算技巧 高频2-gram 高频词条降采样 负采样…...
)
Python 语法糖:让编程更简单(续二)
Python 语法糖:让编程更简单(续) 10. Type hints Type hints 是 Python 中的一种语法糖,用于指定函数或变量的类型。例如: def greet(name: str) -> None:print(f"Hello, {name}!")这段代码将定义一个…...

6 - Shell编程之sed与awk编辑器
目录 一、sed 1.概述 2.sed命令格式 3.常用操作的语法演示 3.1 输出符合条件的文本 3.2 删除符合条件的文本 3.3 替换符合条件的文本 3.4 插入新行 二、awk 1.概述 2. awk命令格式 3.awk工作过程 4.awk内置变量 5.awk用法示例 5.1 按行输出文本 5.2 按字段输出文…...

什么是XML文件,以及如何打开和转换为其他文件格式
本文描述了什么是XML文件以及它们在哪里使用,哪些程序可以打开XML文件,以及如何将XML文件转换为另一种基于文本的格式,如JSON、PDF或CSV。 什么是XML文件 XML文件是一种可扩展标记语言文件。它们是纯文本文件,除了描述数据的传输、结构和存储外,本身什么也不做。 RSS提…...

海外直播对网速、带宽、安全的要求
要满足海外直播的要求,需要拥有合适的网络配置。在全球化的浪潮下,海外直播正逐渐成为企业、个人和各类组织的重要工具。不论是用于市场推广、品牌宣传,还是与观众互动,海外直播都为参与者带来了丰富的机会。然而,确保…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

goreplay
1.github地址 https://github.com/buger/goreplay 2.简单介绍 GoReplay 是一个开源的网络监控工具,可以记录用户的实时流量并将其用于镜像、负载测试、监控和详细分析。 3.出现背景 随着应用程序的增长,测试它所需的工作量也会呈指数级增长。GoRepl…...
