【深度学习】梯度下降法
梯度就是导数,而梯度下降法就是一种通过求目标函数的导数来寻找目标函数最小化的方法。梯度下降目的是找到目标函数最小化时的取值所对应的自变量的值,目的是为了找自变量X。
最优化问题在机器学习中有非常重要的地位,很多机器学习算法最后都归结为求解最优化问题。最优化问题是求解函数极值的问题,包括极大值和极小值。在各种最优化算法中,梯度下降法是最简单、最常见的一种,在深度学习的训练中被广为使用。
1. 梯度下降理解
梯度下降法的基本思想可以类比为一个下山的过程。

按照梯度下降算法的思想,它将按如下操作达到最低点:
- 明确自己现在所处的位置
- 找到相对于该位置而言下降最快的方向
- 沿着第二步找到的方向走一小步,到达一个新的位置,此时的位置肯定比原来低
- 回到第一步
- 终止于最低点
按照以上5步,最终达到最低点,这就是梯度下降的完整流程。当然你可能会说,上图不是有不同的路径吗?是的,因为上图并不是标准的凸函数,往往不能找到最小值,只能找到局部极小值。所以可以用不同的初始位置进行梯度下降,来寻找更小的极小值点。
2. 算法解释
我们知道,对于一个逻辑回归函数,我们可以得到其代价函数,用代价函数来衡量模型预测值与真实值之间差异的函数。
定义一个公式如下,J是关于w和b的一个函数,我们在山林里当前所处的位置为 点,要从这个点走到J的最小值点,也就是山底。首先我们先确定前进的方向,也就是梯度的反向,然后走一段距离的步长,也就是α,走完这个段步长,就到达了
这个点。
α在梯度下降算法中被称作为学习率(learning rate)或者步长(stride),意味着我们可以通过α来控制每一步走的距离,以保证不要步子跨的太大,其实就是不要走太快,错过了最低点。同时也要保证不要走的太慢,导致太阳下山了,还没有走到山下。所以α的选择在梯度下降法中往往是很重要的,α不能太大也不能太小,太小的话,可能导致迟迟走不到最低点,太大的话,会导致错过最低点。

3. m个样本的梯度下降
损失函数 的定义如下:

当算法输出关于样本y 的 ,
是训练样本的预测值,即:
。 在前面展示的是对于任意单个训练样本
,
和
添上上标 i 表示你求得的相应的值。带有求和的全局代价函数,实际上是1到m 项各个损失的平均。 所以它表明全局代价函数对
的微分,对
的微分也同样是各项损失对
微分的平均。

为什么、
、
、
表达式是这样的呢?

4. 代码
J=0;dw1=0;dw2=0;db=0;
for i = 1 to mz(i) = wx(i)+b;a(i) = sigmoid(z(i));J += -[y(i)log(a(i))+(1-y(i))log(1-a(i));dz(i) = a(i)-y(i);dw1 += x1(i)dz(i);dw2 += x2(i)dz(i);db += dz(i);
J/= m;
dw1/= m;
dw2/= m;
db/= m;
w=w-alpha*dw
b=b-alpha*db
相关文章:

【深度学习】梯度下降法
梯度就是导数,而梯度下降法就是一种通过求目标函数的导数来寻找目标函数最小化的方法。梯度下降目的是找到目标函数最小化时的取值所对应的自变量的值,目的是为了找自变量X。 最优化问题在机器学习中有非常重要的地位,很多机器学习算法最后都…...

基于机器学习的电商优惠券核销预测
1. 项目简介 随着移动互联网的快速发展,O2O(Online to Offline)模式已成为电商领域的一大亮点。优惠券作为一种有效的营销工具,被广泛应用于吸引新客户和激活老用户。然而,传统的随机投放方式往往效率低下,…...

PHP-FPM 远程代码执行漏洞(CVE-2019-11043)复现
启动环境 切换目录到vulhub/php/CVE-2019-11043下 查看端口 访问 安装漏洞利用工具 git clone https://github.com/neex/phuip-fpizdam.git 安装go语言 # 1、下载go,这里使用 go1.22.5 版本,可替换为最新版本 wget https://dl.google.com/go/go1.22.5.…...

Rust : 从事量化的生态现状与前景
Rust适不适合做量化工作? 一般地认为,目前大部分场景策略开发最佳是Python;策略交易和部署是C。但还是有人会问,Rust呢? 这个问题不太靠谱! 适不适合做一件事情,本身就是一件主观的事。即使是…...

Java项目——苍穹外卖(一)
Entity、DTO、VO Entity(实体) Entity 是表示数据库表的对象,通常对应数据库中的一行数据。它通常包含与数据库表对应的字段,并可能包含一些业务逻辑。 DTO(数据传输对象) 作用:DTO 是用于在…...

20240908 每日AI必读资讯
新AI编程工具爆火:手机2分钟创建一个APP! - AI初创公司Replit推出的智能体——Replit Agent。开发环境、编写代码、安装软件包、配置数据库、部署等等,统统自动化! - 操作方式也是极其简单,只需一个提出Prompt的动作…...

HNU-2023电路与电子学-实验3
写在前面: 本次实验是完成cpu设计的剩余部分,整体难度比上一次要小,细心完成就能顺利通过全部测评 一、实验目的 1.了解简易模型机的内部结构和工作原理。 2.分析模型机的功能,设计 8 重 3-1 多路复用器。 3.分析模型机的功能…...

html基础语法 看这一篇就够了!
HTML 一 概念 html:html 文件根标签 head:编写页面相关的属性 title:页面标题 body:页面内容展示信息 二 DOM 树: 所有的标签都是 html 的子标签 head 和 body 是兄弟标签,同一级别 head 和 title 为父子标签 1.第一个程序 <html><head>…...
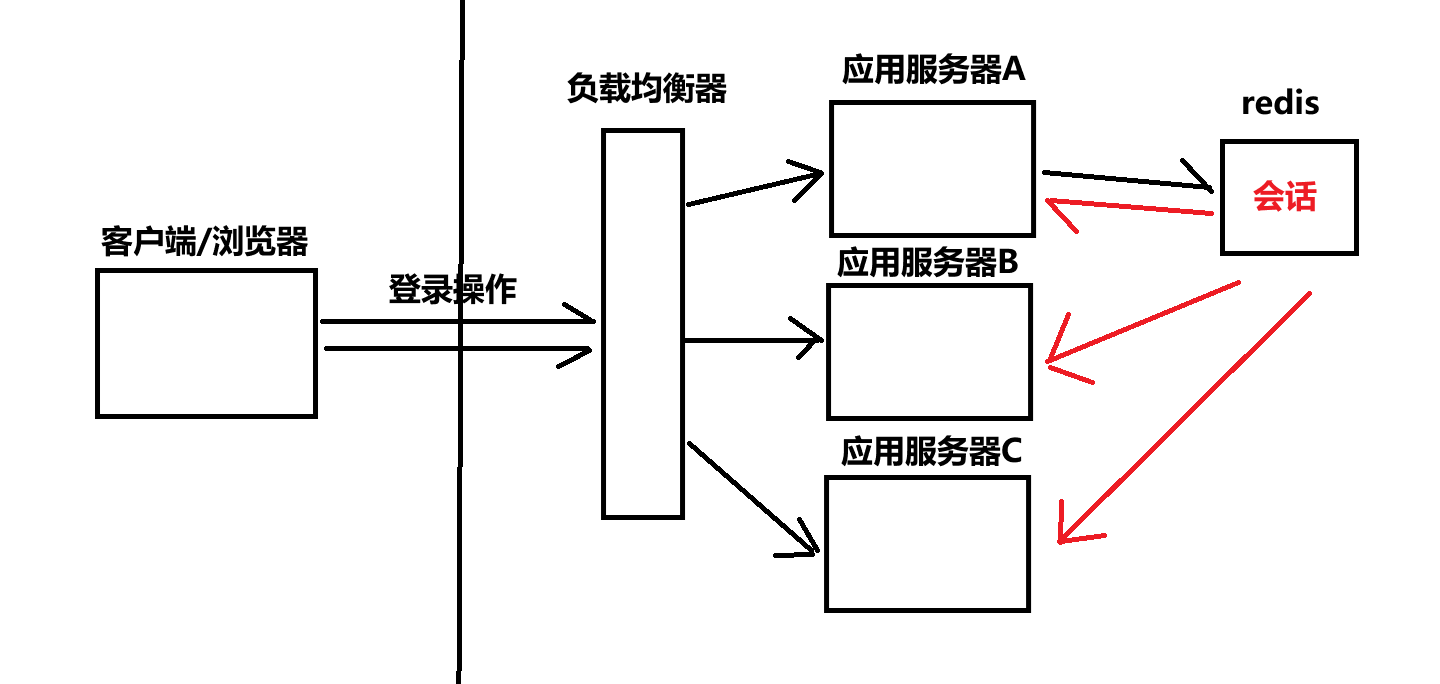
【redis】redis的特性和主要应用场景
文章目录 redis 的特性在内存中存储数据可编程的扩展能力持久化集群高可用快 redis 的应用场景实时数据存储缓存消息队列 redis 的特性 redis 的一些特性(优点)成就了它 在内存中存储数据 In-memory data structures MySQL 主要是通过“表”的方式来…...

部署后端WebSocket服务到AWS云服务器
目录 1.创建AWS账户2.选择EC2实例3.配置EC2实例4.使用VSCode连接到EC2实例5.部署WebSocket服务6.配置域名和SSL(可选)7.监控和维护 1.创建AWS账户 如果你还没有AWS账户,你需要先在AWS官网注册一个。 2.选择EC2实例 登录到AWS管理控制台。搜…...

常见的集合
1、Collection 单列集合的根接口 遍历方法 Collection<String> c new ArrayList<>(); c.add("赵敏"); c.add("小昭"); c.add("素素"); c.add("灭绝"); System.out.println(c); //[赵敏, 小昭, 素素, 灭绝]//1、迭代器遍…...

Swift知识点---RxSwift学习
1. 什么是RxSwift RxSwift是Swift函数响应式编程的一个开源库,由Github的ReactiveX组织开发、维护 RxSwift的目的是:让数据/事件流 和 异步任务能够更方便的序列化处理,能够使用Swift进行响应式编程 RxSwift本质上还是观察者模式ÿ…...

驾驭不断发展的人工智能世界
从很多方面来看,历史似乎正在重演。许多企业正争相采用生成式人工智能 (Gen AI),就像它们争相采用云计算一样,原因也是一样的:效率、成本节约和竞争优势。 然而,与云一样,GenAI 仍是一项发展中的技术&…...
冒泡排序——基于Java的实现
简介 冒泡排序(Bubble Sort)是一种简单的排序算法,适用于小规模数据集。其基本思想是通过重复遍历待排序的数组,比较相邻的元素并交换它们的位置,以此将较大的元素逐步“冒泡”到数组的末尾。算法的名称源于其运行过程…...
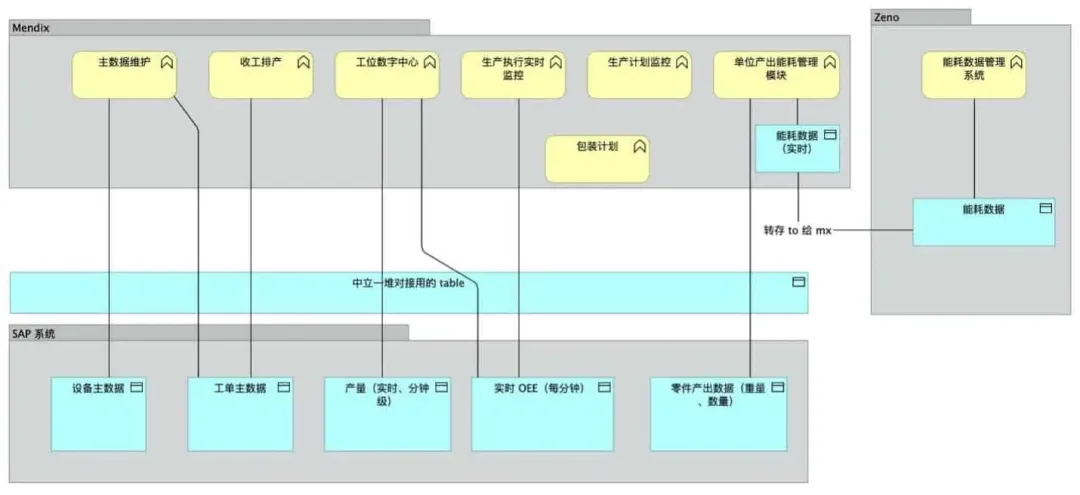
Mendix 创客访谈录|Mendix赋能汽车零部件行业:重塑架构,加速实践与数字化转型
在当前快速发展的技术时代,汽车行业正经历着前所未有的数字化转型。全球领先的汽车零配件制造商面临着如何利用最新的数字技术优化其制造车间管理的挑战。从设备主数据管理到生产执行工单管理,再到实时监控产量及能耗,需要一个灵活、快速且高…...

船舶机械设备5G智能工厂物联数字孪生平台,推进制造业数字化转型
船舶机械设备5G智能工厂物联数字孪生平台,推进制造业数字化转型。在当今数字化浪潮推动下,船舶制造业正经历着前所未有的变革。为了应对市场的快速变化,提升生产效率,降低成本,并增强国际竞争力,船舶机械设…...

什么是jsonp请求
JSONP(JSON with Padding)是一种解决跨域请求问题的技术。它允许网页从不同的域名请求数据,而不受同源策略的限制。JSONP 通过动态创建 script 标签来实现跨域请求,因为 script 标签不受同源策略的限制。 一、工作原理 客户端&a…...

【C++】STL容器详解【上】
目录 一、STL基本概念 二、STL的六大组件 三、string容器常用操作 3.1 string 容器的基本概念 3.2 string 容器常用操作 3.2.1 string 构造函数 3.2.2 string基本赋值操作 3.2.3 string存取字符操作 3.2.4 string拼接字符操作 3.2.5 string查找和替换 3.2.6 string比…...

助贷行业的三大严峻挑战:贷款中介公司转型债务重组业务
大家是否察觉到一种趋势?现如今,众多贷款辅助服务机构与专注于债务再构的公司之间形成了紧密的“联动”。有的选择将获取的贷款需求转介给债务重组方,有的则直接下场,动用自身资本参与债务重组业务。这一现象背后,究竟…...

力扣第42题 接雨水
前言 记录一下刷题历程 力扣第42题 接雨水 接雨水 原题目:给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2,1] 输出&…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...
