闯关leetcode——3.Longest Substring Without Repeating Characters
大纲
- 题目
- 地址
- 内容
- 解题
- 代码地址
题目
地址
https://leetcode.com/problems/longest-substring-without-repeating-characters/description/
内容
Given a string s, find the length of the longest substring without repeating characters.
Example 1:
Input: s = “abcabcbb”
Output: 3
Explanation: The answer is “abc”, with the length of 3.
Example 2:
Input: s = “bbbbb”
Output: 1
Explanation: The answer is “b”, with the length of 1.
Example 3:
Input: s = “pwwkew”
Output: 3
Explanation: The answer is “wke”, with the length of 3.
Notice that the answer must be a substring, “pwke” is a subsequence and not a substring.
Constraints:
- 0 <= s.length <= 5 * 104
- s consists of English letters, digits, symbols and spaces.
解题
这题是要在一个只包含English letters, digits, symbols and spaces的字符串中找打最长的不重复子串。
一种比较容易想到的思路是:遇到重复的字符,则从上次这个字符出现的位置的后个位置开始尝试比较。比如abcdef是当前最长不重复子串。如果后面出现的字符是b,则从下标为1的b的后一位(c)开始组成新的测试子串,即cdefb。当新的测试子串的长度大于当前最长的子串,则更新该最大长度值。
为了判断后续出现的字符是否已经存在于当前最长子串中,则可以考虑使用map<char,int>的结构来存储最长子串及其坐标信息。但是这个题目存在只包含English letters, digits, symbols and spaces的条件,这意味着每个字符都是ASCII码中的字符——它只有128个——且是连续的数字(见https://baike.baidu.com/item/ASCII/309296)。我们可以充分利用这个条件,使用一个更加紧凑高效的结构来存储这个关系。
array<int, 128> charIndex;charIndex.fill(-1);
然后我们遍历整个字符串,将这样的关系存储起来。
for (int i = 0; i < s.size(); i++) {
……charIndex[int(s[i])] = i;
……
}
这儿有一个问题:在寻找过程中,如果最长子串发生了变化,则被剔除出的字符串是否应该从charIndex中剔除?比如上例abcdef是最长子串时,charIndex包含这些字符以及它们的位置。如果在f后面新出现的字符是b,则要开始新探索的子串是cdefb,这个时候字符a是否需要从charIndex中剔除?因为它可能会影响到后续再次出现a时的判断。实际我们通过新探索的子串开头第一个字符位置来判断新的重复是否需要处理。在这个例子中,第一个a(绿色)位于新子串cdefb起始位置(箭头处)的左侧,即使它存在charIndex中,也不会影响后续的探索,即我们可将新的探索子串定义为cdefba。假设下一个出现的是字符d,由于上一次出现的d位于子串起始位置(箭头处)的右侧,所以需要重新探索新的子串

经过分析,我们知道子串起始位置也是需要记录,以用于辅助判断是否要使用新子串。
由于该题只是要输出最长子串长度,并不要求输出最长子串的内容,所以我们并不用记录子串的具体顺序,只要比较并保留最长的一条串的长度即可。
最长串的比较maxLen = max(maxLen, i - start)可以优化到串的起始位置发生变化的时候进行。这样可以将对比的次数降到最低。
#include <string>
#include <array>
using namespace std;class Solution {
public:int lengthOfLongestSubstring(string s) {array<int, 128> charIndex;charIndex.fill(-1);int start = 0;int maxLen = 0;for (int i = 0; i < s.size(); i++) {if (charIndex[int(s[i])] >= start) {maxLen = max(maxLen, i - start);start = charIndex[int(s[i])] + 1;}charIndex[int(s[i])] = i;}if (s.size() - start > maxLen) {maxLen = s.size() - start;}return maxLen;}
};
上述代码的一个边界问题是:最长子串的尾部正好是原始串的尾部。这样我们必须在遍历结束后,考虑这种情况下最长子串的可能性。

代码地址
https://github.com/f304646673/leetcode/tree/main/3-Longest-Substring-Without-Repeating-Characters
相关文章:

闯关leetcode——3.Longest Substring Without Repeating Characters
大纲 题目地址内容 解题代码地址 题目 地址 https://leetcode.com/problems/longest-substring-without-repeating-characters/description/ 内容 Given a string s, find the length of the longest substring without repeating characters. Example 1: Input: s “abc…...
)
Android Radio2.0——公告注册及监听(三)
前面文章内容介绍了 Radio 相关功能的设置,我们知道可以通过设置来监听不同内容的广播公告,但是在开启对应功能的同时,还需要先注册对应公告监听,这里我们就来看一下广播公告监听的注册流程。 一、注册公告 1、接口封装 private final AtomicBoolean mHasRegisterTa = n…...

【C++】类和对象(三)再探构造函数|static成员函数|友元函数|内部类|匿名对象|对象拷贝时的编译优化
欢迎来到HarperLee的学习笔记! 一、再探构造函数 初始化列表:构造函数初始化的第二种方式(第一种是使用函数体内赋值)。使用方式:以一个冒号:开始,用逗号,分隔数据成员列表,每个成员变量后面跟…...

2024中国算力大会 2024 China Computational Power Conference
文章目录 一、会议详情二、重要信息三、大会介绍四、出席嘉宾五、征稿主题六、咨询 一、会议详情 二、重要信息 大会官网:https://ais.cn/u/vEbMBz提交检索:EI Compendex、IEEE Xplore、Scopus会议时间:2024年9月27-29日会议地点:…...

jEasyUI 扩展行显示细节
jEasyUI 扩展行显示细节 jEasyUI 是一个基于 jQuery 的前端框架,它提供了一系列的 UI 组件,使得 Web 应用的界面开发变得更加简单快捷。在 jEasyUI 的表格(datagrid)组件中,扩展行显示细节是一个常用的功能,它允许用户通过点击一行来展开更多的信息,这样可以有效地展示…...
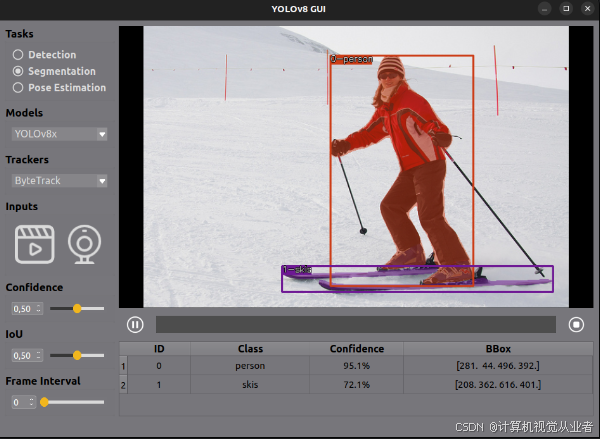
YOLOv8+Deepsort+PyQt+GUI 语义分割+目标检测+姿态识别 三者合一(集成于一套系统)综合视觉分析系统
综合视觉分析系统 技术栈: YOLOv8:用于目标检测,是一个快速且准确的目标检测框架。DeepSORT:用于目标跟踪,结合了深度学习特征提取和卡尔曼滤波器来预测目标轨迹。GUI:提供一个直观易用的图形用户界面&am…...

机器学习无监督学习
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl1. 无监督学习概述 1.1 定义与特点 无监督学习是一种数据挖掘技术,它允许机器通过观察数据来学习数据的内在结构和模式,而无需预先标注的输出变量。这种方法特别适用于数据探索和发现隐藏在数据…...

windows10-VMware17-Ubuntu-22.04-海康2K摄像头兼容问题,求解(已解决)
文章目录 1.webrtc camera测试2.ffmpeg 测试3.Ubuntu 自带相机4.解决办法 环境:windows10系统下,VMware的Ubuntu-22.04系统 问题:摄像头出现兼容问题,本来是想开发测试的,Ubuntu方便些。买了海康2K的USB摄像头…...

【系统架构设计师】解释器模式
解释器模式(Interpreter Pattern)是一种行为型设计模式,它定义了文法的表示,并定义了一个解释器,该解释器使用该表示来解释语言中的句子。在解释器模式中,通常包括一个抽象语法树(Abstract Synt…...

Hive原理剖析
1. 概述 背景介绍 Apache Hive是一个基于Hadoop的开源数据仓库软件,为分析和管理大量数据集提供了SQL-like的接口。最初由Facebook开发并贡献给Apache,Hive现已成为大数据处理领域的重要工具之一。它将传统的SQL功能与Hadoop的强大分布式处理能力结合&…...

在 Ubuntu 上查看重复文件
一般情况下 1. 使用 fdupes 工具 fdupes 是一个专门用于查找重复文件的工具。 安装: sudo apt-get install fdupes 使用: fdupes -r /path/to/directory -r 选项会递归查找子目录中的重复文件。 2. 使用 rmlint 工具 rmlint 是另一个强大的重复文件查找工具…...

docker容器高效连接 Redis 的方式
在微服务架构中,Redis 是一种常见的高效缓存解决方案,通常用于存储临时数据、会话信息或 token。如何在服务容器中高效、稳定地连接 Redis 是架构设计中的一个重要环节。 这篇博客将以实际项目为例,详细介绍如何配置 Flask 应用中的服务容器…...

手撕Python之生成器、装饰器、异常
1.生成器 生成器的定义方式:在函数中使用yield yield值:将值返回到调用处 我们需要使用next()进行获取yield的返回值 yield的使用以及生成器函数的返回的接收next() def test():yield 1,2,3ttest() print(t) #<generator object test at 0x01B77…...

LabVIEW步进电机控制方式
在LabVIEW中控制步进电机可以通过多种方式实现。每种方法都有其独特的优缺点,适用于不同的应用场合。下面详细介绍几种常见的步进电机控制方式,并进行比较。 1. 开环控制(Open-Loop Control) 特点 通过定期发出脉冲信号来控制步进…...

vllm源码解析(五):LLM模型推理
八 模型推理细节探索 8.1 回顾下step的流程 def step(self) -> List[Union[RequestOutput, EmbeddingRequestOutput]]:# 多GPU并行推理时走AsyncLLMEngine分支。如果进入当前LLMEngine,性能会下降,这里会抛出异常。if self.parallel_config.pipeline_parallel_s…...
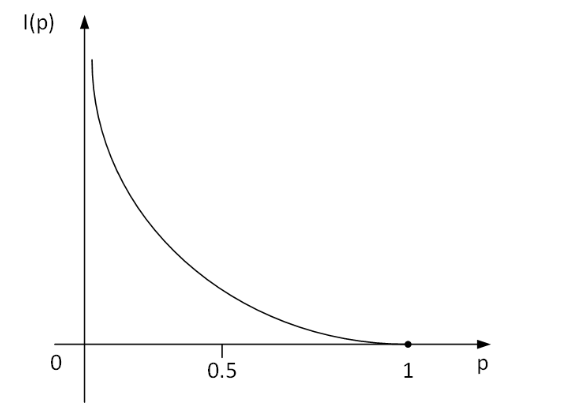
数学建模笔记——熵权法(客观赋权法)
数学建模笔记——熵权法[客观赋权法] 熵权法(客观赋权法)1. 基本概念2. 基本步骤3. 典型例题3.1 正向化矩阵3.2 对正向化矩阵进行矩阵标准化3.3 计算概率矩阵P3.4 计算熵权3.5 计算得分 4. python代码实现 熵权法(客观赋权法) 1. 基本概念 熵权法,物理学名词,按照信息论基本原…...

XGBoost算法-确定树的结构
我们在求解上面的w和obj的过程中,都是假定我们的树结构是确定的,因为当我们改变树中划分条件的时候,每个叶子节点对应的样本有可能是不一样的,我们的G和H也是不一样的,得到的最优w和最优obj肯定也是不一样的。 到底哪一…...

concurrentHashMap线程安全实现的原理
1. Segment 数组 ConcurrentHashMap 内部维护一个 Segment 数组,每个 Segment 都是一个小型的 HashMap。Segment 继承自 ReentrantLock,因此每个 Segment 都是一个可重入锁。 2. 并发级别 ConcurrentHashMap 在构造时可以指定并发级别(con…...

域名证书,泛域名证书,sni
文章目录 前言一、证书1.全域名证书2.泛域名证书 二、域名证书的使用1、浏览器请求域名证书流程对全域名证书的请求流程对泛域名证书的请求流程ssl client-hello携带server name 报文 2、浏览器对证书的验证流程 三、域名证书和sni 前言 本文介绍了泛域名证书和全域名证书的区别…...

Pytest夹具autouse参数使用。True表示会自动在测试中使用,而无需显式指定
1. 全局conftest文件日志记录功能 # 当前路径(使用 abspath 方法可通过dos窗口执行) current_path os.path.dirname(os.path.abspath(__file__)) # 上上级目录 ffather_path os.path.abspath(os.path.join(current_path,"../"))LOG_FILE_PATH f{ffather_path}/lo…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...
