数据结构之红黑树的 “奥秘“

目录：

一.红黑树概念

二. 红黑树的性质

三.红黑树的实现

四.红黑树验证 

五.AVL树和红黑树的比较

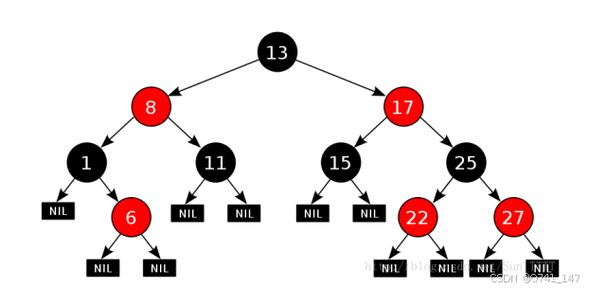
一.红黑树概念

1.红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。 通过对任何 一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近 平衡的。

---

---

二. 红黑树的性质:

1. 每个结点不是红色就是黑色

2. 根节点是黑色的

3. 如果一个节点是红色的，则它的两个孩子结点是黑色的【没有2个连续的红色节点】

4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点也就是（每条路径的黑色节点数相等）

5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)

总结性质：最长路径最多是最短路径的2倍.

总结性质推导：

---

---

三.红黑树的实现：

1.红黑树节点的定义 :

这里注意我们定义一个枚举来储存红黑树节点的颜色

public class RBTree {static class RBTreeNode {public RBTreeNode left;public RBTreeNode right;public RBTreeNode parent;public int val;public COLOR color;//枚举public RBTreeNode(int val) {this.val = val;//新创建的节点默认是红色this.color = COLOR.RED;}}public RBTreeNode root;
}

 

2.红黑树的插入:

这里我们要围绕红黑树上面的几条性质构建红黑树；但是红黑树是在二叉搜索树的基础上加上其平衡限制条件，所有我们构建时可以借鉴二叉搜索树方式。

步骤一：和二叉二叉搜索树一样找到要插入的节点；

步骤二：调整插入的节点让其满足红黑树的性质；

所有我们构建红黑树总共有三种情况

这里注意：插入节点默认为红色节点，推导如下：

3.构建红黑树的有三种情况:

3.1.情况一: cur为红，p为红，g为黑，u存在且为红:

图解：

代码：

 //开始调整颜色while (parent != null && parent.color == COLOR.RED) {RBTreeNode grandParent = parent.parent;/**情况一：** cur为红，p为红，g为黑，uncle存在且为红**  parent在grandParent左边，uncle在grandParent右边*/if (parent == grandParent.left) {RBTreeNode uncle = grandParent.right;if (uncle != null && uncle.color == COLOR.RED) {parent.color = COLOR.BLACK;uncle.color = COLOR.BLACK;grandParent.color = COLOR.RED;//预防grandParent的父亲为红色，就还有子树,继续向上修改cur = grandParent;parent = cur.parent;}

3.2.情况二: cur为红，p为红，g为黑，u不存在或者u为黑:

这里注意要先grandParent右旋，然后再调整颜色，parent改为 黑色，grandParent改为红色

 图解：

代码：

/** 情况二：
* cur为红，p为红，g为黑，uncle为黑色，或者uncle不存在
*
*  方法：
*  1.先右单旋
*  2.再改颜色*/
rotateRight(grandParent);
parent.color = COLOR.BLACK;
grandParent.color = COLOR.RED;

3.3.情况三: 调整过程中，cur为红，p为红，g为黑，u不存在/u为黑：

这里先左旋parent，再把parent 和 cur 的引用交换变为和情况二类似，再当作情况二处理（右旋改颜色，图片上笔误是右旋）

代码：

/*** 情况三：
* 先左单旋parent
* 再交换parent和cur的引用,变成情况二处理
*/
if (parent.right == cur) {
rotateLeft(parent);
RBTreeNode tmp = parent;
parent = cur;
cur = tmp;}//变成情况二

 

当parent == grandParent.right，和上面三种情况完全相反，为镜相关系。

插入全部代码如下：

public class RBTree {static class RBTreeNode {public RBTreeNode left;public RBTreeNode right;public RBTreeNode parent;public int val;public COLOR color;//枚举public RBTreeNode(int val) {this.val = val;//新创建的节点默认是红色this.color = COLOR.RED;}}public RBTreeNode root;//插入：public boolean insert(int val) {RBTreeNode node = new RBTreeNode(val);if (root == null) {root = node;//插入节点默认为红色所有，当root为空时，要把插入的节点变为黑色root.color = COLOR.BLACK;return true;}RBTreeNode cur = root;RBTreeNode parent = null;while (cur != null) {if (cur.val < val) {parent = cur;cur = cur.right;} else if (cur.val > val) {parent = cur;cur = cur.left;} else {return false;}}if (parent.val < val) {parent.right = node;} else {parent.left = node;}node.parent = parent;cur = node;//指向新插入的节点//开始调整颜色while (parent != null && parent.color == COLOR.RED) {RBTreeNode grandParent = parent.parent;/**情况一：** cur为红，p为红，g为黑，uncle存在且为红**  parent在grandParent左边，uncle在grandParent右边*/if (parent == grandParent.left) {RBTreeNode uncle = grandParent.right;if (uncle != null && uncle.color == COLOR.RED) {parent.color = COLOR.BLACK;uncle.color = COLOR.BLACK;grandParent.color = COLOR.RED;//预防grandParent的父亲为红色，就还有子树,继续向上修改cur = grandParent;parent = cur.parent;} else {/*** 情况三：* 先左单旋parent* 再交换parent和cur的引用,变成情况二处理*/if (parent.right == cur) {rotateLeft(parent);RBTreeNode tmp = parent;parent = cur;cur = tmp;}//变成情况二/** 情况二：* cur为红，p为红，g为黑，uncle为黑色，或者uncle不存在**  方法：*  1.先右单旋*  2.再改颜色*/rotateRight(grandParent);parent.color = COLOR.BLACK;grandParent.color = COLOR.RED;}} else {//下面情况和上面情况完全相反//parent == grandParent.rightRBTreeNode uncle = grandParent.left;if (uncle != null && uncle.color == COLOR.RED) {parent.color = COLOR.BLACK;uncle.color = COLOR.BLACK;grandParent.color = COLOR.RED;//预防grandParent的父亲为红色，就还有子树,继续向上修改cur = grandParent;parent = cur.parent;} else {if (parent.left == cur) {rotateRight(parent);RBTreeNode tmp = parent;parent = cur;cur = tmp;}//变成情况二rotateLeft(grandParent);parent.color = COLOR.BLACK;grandParent.color = COLOR.RED;}}}//当parent为空时，要把根节点变为黑色root.color = COLOR.BLACK;return true;}/*** 右单旋* @param parent*/private void rotateRight (RBTreeNode parent){RBTreeNode subL = parent.left;RBTreeNode subRL = subL.right;parent.left = subRL;subL.right = parent;//如果旋转的整棵树也是一个子树，记录下原来该树的父亲，后续修改RBTreeNode pParent = parent.parent;if (subRL != null) {subRL.parent = parent;}parent.parent = subL;//看看整棵树是否也是一个子树if (parent == root) {root = subL;root.parent = null;} else {//是子树就确定这棵树是左子树还是右子树if (pParent.left == parent) {pParent.left = subL;} else {pParent.right = subL;}}subL.parent = pParent;}/*** 左单旋* @param parent*/private void rotateLeft (RBTreeNode parent){RBTreeNode subR = parent.right;RBTreeNode subRL = subR.left;parent.right = subRL;subR.left = parent;RBTreeNode pParent = parent.parent;if (subRL != null) {subRL.parent = parent;}parent.parent = subR;//看看整棵树是否也是一个子树if (parent == root) {root = subR;root.parent = null;} else {//是子树就确定这棵树是左子树还是右子树if (pParent.left == parent) {pParent.left = subR;} else {pParent.right = subR;}}subR.parent = pParent;}
}

---

---

四.红黑树验证：

1.红黑树的检测分为两步：

步骤一： 检测其是否满足二叉搜索树(中序遍历是否为有序序列）

步骤二：检测其是否满足红黑树的性质 

 

步骤一： 检测其是否满足二叉搜索树(中序遍历是否为有序序列）：

代码：

 /**1. 检测其是否满足二叉搜索树(中序遍历是否为有序序列)* 中序遍历：* @param root*/public void inorder(RBTreeNode root){if(root == null){return;}inorder(root.left);System.out.print(root.val+ " ");inorder(root.right);}

步骤二：检测其是否满足红黑树的性质 :

//2.检测其是否满足红黑树的性质:public boolean isRBTree(){if(root == null){//空树也是红黑树return true;}if(root.color != COLOR.BLACK){System.out.println("违反了性质2：根节点不是黑色");return false;}RBTreeNode cur = root;//blackNum是事先计算好一边黑色节点的个数int blackNum = 0;while (cur != null){if (cur.color == COLOR.BLACK){blackNum++;}cur = cur.left;}//判断性质三有没有两个红色的节点 && 判断性质四：每条路径的黑色节点个数是否相等return checkRedColor(root) && checkBlackNum(root,blackNum,0);}/*** 判断性质三有没有两个红色的节点：* 思路：遍历当前二叉树节点如果是红色，则判断他的父亲节点是不是红色* @param root* @return*/private boolean checkRedColor(RBTreeNode root){if(root == null){return true;}if (root.color == COLOR.RED){RBTreeNode parent = root.parent;if (parent != null && parent.color == COLOR.RED){System.out.println("违反了性质三: 连续出现两个红色的节点");return false;}}return checkRedColor(root.left) && checkRedColor(root.right);}/***判断性质四：每条路径的黑色节点个数是否相等* @param root* @param blackNum:事先计算好黑色节点的个数* @param pathBlackNum：每次递归计算的黑色节点的个数* 思路：看 blackNum 和 pathBlackNum 的数量是否相等* @return*/private boolean checkBlackNum(RBTreeNode root,int blackNum, int pathBlackNum){if(root == null){return true;}if (root.color == COLOR.BLACK){pathBlackNum++;}//blackNum 和 pathBlackNum 的数量是否相等就不满足性质if (root.left == null && root.right == null){if(pathBlackNum != blackNum){System.out.println("违反了性质四：每条路径的黑色节点个数不相等了！");return false;}}return checkBlackNum(root.left,blackNum,pathBlackNum)&& checkBlackNum(root.right,blackNum,pathBlackNum);}

  

---

---

五.AVL树和红黑树的比较

红黑树和AVL树都是高效的平衡二叉树，增删改查的时间复杂度都是O(log2^n)，红黑树不追求绝对平衡，其只需保 证最长路径不超过最短路径的2倍(相对平衡)，相对而言，降低了插入和旋转的次数，所以红黑树在经常进行增删的结构中性能比 AVL树更优，而且红黑树实现比较简单，所以实际运用中红黑树更多。 

 

补充：java集合框架中的：TreeMap、TreeSet底层使用的就是红黑树