数据结构之折半查找
折半查找(Binary Search),也称为二分查找,是一种在有序数组中查找特定元素的搜索算法。其工作原理是,通过不断将待查找的区间分成两半,并判断待查找的元素可能存在于哪一半,然后继续在存在可能性的那一半区间中查找,直到找到该元素或者区间被缩小为0为止。
折半查找的基本步骤
1、初始化:
确定查找范围的上下界,即查找区间的起始位置low和结束位置high,通常初始时low = 0,high = 数组长度 - 1。
2、循环查找:
当low <= high时,执行以下步骤:
计算中间位置mid = (low + high) // 2(注意使用整除以避免浮点数)。
判断中间位置的元素是否是要查找的元素,即arr[mid] == target:
如果是,则查找成功,返回中间位置mid(或该位置的索引mid,取决于具体实现)。
如果不是,则判断target与arr[mid]的大小关系,并据此调整查找范围:
如果target < arr[mid],则说明target在左半部分,更新high = mid - 1。
如果target > arr[mid],则说明target在右半部分,更新low = mid + 1。
3、查找失败:
如果循环结束时仍未找到target,则说明数组中不存在该元素,返回查找失败的信息(通常是-1或特定值)。
折半查找的Python示例
def binary_search(arr, target):"""折半查找(二分查找):param arr: 有序数组:param target: 要查找的目标值:return: 目标值在数组中的索引,如果未找到则返回-1"""low, high = 0, len(arr) - 1while low <= high:mid = (low + high) // 2if arr[mid] == target:return mid # 找到目标值,返回索引elif arr[mid] < target:low = mid + 1 # 调整查找范围到右半部分else:high = mid - 1 # 调整查找范围到左半部分return -1 # 未找到目标值,返回-1# 示例
arr = [1, 3, 5, 7, 9, 11, 13, 15, 17, 19]
target = 7result = binary_search(arr, target)
print(f"元素{target}在数组中的索引为:{result}") # 输出:元素7在数组中的索引为:3
折半查找的优缺点
优点:
查找速度快,时间复杂度为O(log n),其中n是数组的长度。
对于大数据集,查找效率远高于顺序查找。
缺点:
要求待查找的数组必须是有序的。
数组必须有随机访问的能力,即可以使用索引直接访问元素,这限制了它在链表等数据结构上的应用。
当数据集非常大时,需要较大的内存空间来存储整个数组。
相关文章:

数据结构之折半查找
折半查找(Binary Search),也称为二分查找,是一种在有序数组中查找特定元素的搜索算法。其工作原理是,通过不断将待查找的区间分成两半,并判断待查找的元素可能存在于哪一半,然后继续在存在可能性…...

linux高级学习12
24.9.9学习目录 一.条件变量 一.条件变量 通常条件变量和互斥锁同时使用; 条件变量是用来阻塞线程,其本身并不是锁,直到达到特定的要求; (1)条件变量初始化 #include <pthread.h> int pthread_con…...
)
leetcode:3174 清除数字 使用栈,时间复杂度O(n)
3174 清除数字 题目链接 题目描述 给你一个字符串 s 。 你的任务是重复以下操作删除 所有 数字字符: 删除 第一个数字字符 以及它左边 最近 的 非数字 字符。 请你返回删除所有数字字符以后剩下的字符串。 示例 1: 输入:s "abc…...

神经网络卷积操作
文章目录 一、nn.Conv2d二、卷积操作原理三、代码实现卷积操作 一、nn.Conv2d nn.Conv2d 是 PyTorch 中的一个类,它代表了一个二维卷积层,通常用于处理图像数据。在深度学习和计算机视觉中,卷积层是构建卷积神经网络(CNN…...

专题二_滑动窗口_算法专题详细总结
目录 滑动窗口,引入: 滑动窗口,本质:就是同向双指针; 1.⻓度最⼩的⼦数组(medium) 1.解析:给我们一个数组nums,要我们找出最小子数组的和target,首先想到的…...

【机器学习-三-无监督学习】
无监督学习 什么是无监督学习分类聚类降维 有监督和无监督学习的区别 上一节介绍了监督学习,下面来介绍无监督学习,这也是最广泛应用的算法。 什么是无监督学习 上一节中,我们知道了监督学习是通过 对算法,**输入一对数据&#x…...
)
JAVA基础:Lambda表达式(上)
前言 Lambda表达式是jdk1.8的一个新特性,他属于一种语法堂主要作用是对匿名内部类语法简化 lambda基本应用 lambda表达式想要优化匿名内部类是有前提条件,首先必须是一个接口,而且要求接口中只能有1个抽象方法,称之为函数式接口…...

Vue使用fetch获取本地数据
(1)使用get test.json文件 { "list":[111,222,333] } <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initi…...

《酒饮真经》秘籍4,让你的酒场技巧更上一层楼!
在酒桌这一独特的舞台上,每个人都扮演着不同的角色,或攻或守,尽显智慧与风度。对于不擅长喝酒的人来说,如何在推杯换盏间既保护自己又不失礼节,是值得我们仔细研究的。下面是酱酒亮哥为您整理的一系列实用的酒桌攻防秘…...

回车符与快捷键记录
一.在Windows和Linux操作系统中,回车符(或称为换行符)的处理方式区别 1.Windows下的回车符 在Windows系统中,回车符通常是由两个字符组成的序列:回车符(Carriage Return,简称CR,AS…...
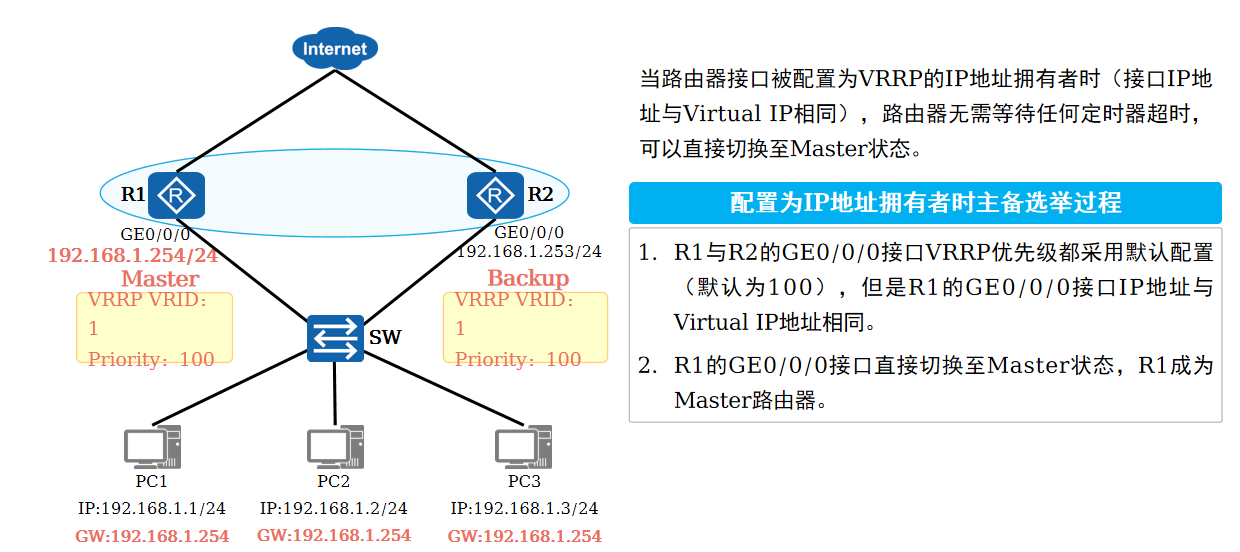
计算机网络-VRRP工作原理
一、VRRP工作原理 前面我们大概了解了VRRP的一些基础概念,现在开始学习VRRP的技术原理。VRRP的选举及工作步骤: 确定网关地址 选举主备 主设备发送VRRP报文通知Backup设备 主设备响应终端ARP并维持在Master状态 终端正常发送报文到网关进行转发 因为我们…...

6.5椒盐噪声
在OpenCV中联合C给一张图片加上椒盐噪声(Salt and Pepper Noise)可以通过随机选择像素点并将其置为黑色(0)或白色(255)来实现。椒盐噪声是一种随机噪声,通常表现为图像中的孤立黑点(…...

CSS样式的引用方式以及选择器使用
1. CSS 引用方式 CSS 可以通过三种方式引用到 HTML 文件中: 行内样式(Inline Styles):直接在 HTML 元素中定义样式。内部样式表(Internal CSS):在 HTML 文档的 <head> 部分使用 <sty…...

Python Flask_APScheduler定时任务的正确(最佳)使用
描述 APScheduler基于Quartz的一个Python定时任务框架,实现了Quartz的所有功能。最近使用Flask框架使用Flask_APScheduler来做定时任务,在使用过程当中也遇到很多问题,例如在定时任务调用的方法中需要用到flask的app.app_context()时&#…...

Linux命名管道
通信的前提是让不同的进程看到同一份资源,因为路径是具有唯一性的,所以我们可以使用路径文件名来唯一的让不同进程看到同一份资源,实现没有血缘关系的两个进程进行管道通信 1.指令级 mkfifio(FILENAME,0666) …...
Xinstall助力App全渠道统计,参数传递下载提升用户体验!
在移动互联网时代,App已成为我们日常生活中不可或缺的一部分。然而,对于App开发者来说,如何有效地推广和运营自己的应用,却是一个不小的挑战。尤其是在面对众多渠道、复杂的数据统计和用户需求多样化的情况下,如何精准…...
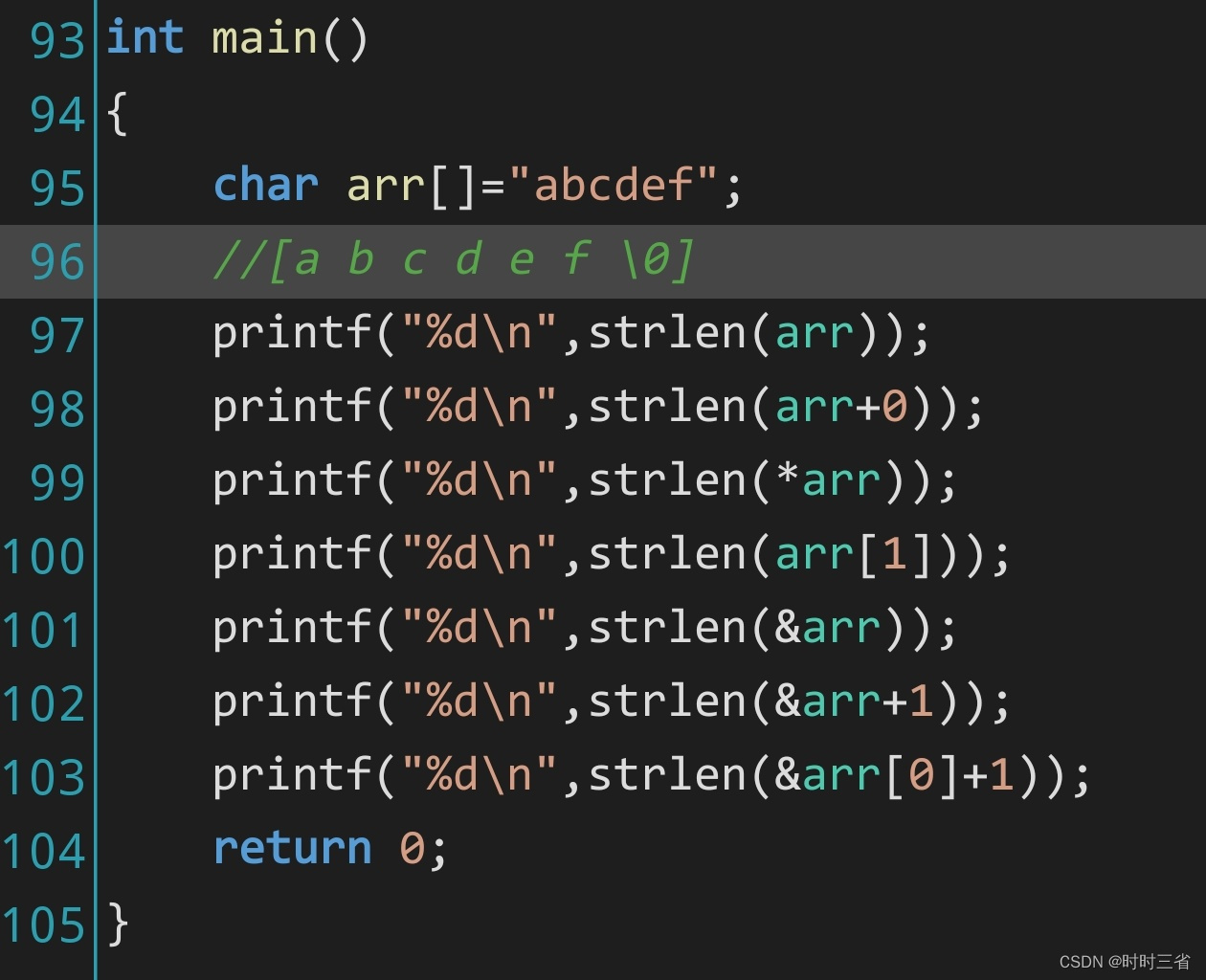
【时时三省】(C语言基础)指针进阶 例题4
山不在高,有仙则名。水不在深,有龙则灵。 ----CSDN 时时三省 strlen是求字符串长度 这个需要算上\0 第一个arr 是打印6 因为它加上\0是有六个元素 第二个arr0 数组名相当于首元素的地址 a的地址加0还是a的地址 所以这个地方还是…...

k8s的配置管理
一、配置管理分为两种: 1. 加密配置:用来保存密码和token密钥对以及其它敏感的k8s资源。 2.应用配置:我们需要定制化的给应用进行配置,我们需要把定制好的配置文件同步到pod当中的容器。 二、加密配置 1.secret三种类型…...

JAVA- 多线程
一,多线程的概念 1.并行与并发 并行:多个任务在同一时刻在cpu 上同时执行并发:多个任务在同一时刻在cpu 上交替执行 2.进程与线程 进程:就是操作系统中正在运行的一个应用程序。所以进程也就是“正在进行的程序”。࿰…...

【Qt】解决设置QPlainTextEdit控件的Tab为4个空格
前言 PyQt5 是一个用于创建跨平台桌面应用程序的 Python 绑定集合,它提供了对 Qt 应用程序框架的访问。用于开发具有图形用户界面(GUI)的应用程序,以及非GUI程序。PyQt5 使得 Python 开发者可以使用 Qt 的丰富功能来构建应用程序。…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...
