最全面的递归算法详解,一篇足矣(高手必备)
在编程中,递归和循环是两种常用的控制结构,各有其独特的优缺点。理解这两者的特点和应用场景,对于编写高效、可读的代码至关重要。
什么是递归?
递归是一种强大的编程技术,允许函数在其定义中调用自身。递归通常涉及两个主要部分:
- 基本情况:这是递归的终止条件,当满足此条件时,函数将不再调用自身。
- 递归情况:这是函数调用自身的部分,通常会将问题规模缩小。

如何写出递归?
只需要做到下面两点
1.终止条件;
2.一般规律,也就是需要重复执行循环的部分。
递归的优点
- 简洁性:递归可以使代码更加简洁,尤其是在处理复杂数据结构(如树和图)时。
- 可读性:递归代码通常比迭代代码更易于理解,因为它直接反映了问题的定义。
- 解决复杂问题:许多算法(如排序和搜索)可以通过递归轻松实现。
递归的缺点
- 性能问题:递归可能导致大量的函数调用,消耗更多的内存和时间,特别是在没有优化的情况下。
- 栈溢出:深度递归可能导致栈溢出错误,因为每次函数调用都会占用栈空间。
Java中的递归实现
以下是一些简单的递归示例,展示了如何在Java中实现递归算法。
1. 计算阶乘
public static int factorial(int n) {if (n == 1) {return 1;} else {return n * factorial(n - 1);}
}2. 斐波那契数列
public static int fibonacci(int n) {if (n == 1 || n == 2) {return 1;} else {return fibonacci(n - 1) + fibonacci(n - 2);}
}3. 反向打印字符串
public static void reversePrint(String str) {if (str.length() == 0) {return;}reversePrint(str.substring(1));System.out.print(str.charAt(0));
}4. 1递归二分查找
//递归二分查找public static int binarySearch(int[] arr,int i, int j,int target) {int m = (i+j) >> 1;if (i > j)return -1;if (arr[m] < target)return binarySearch(arr, m+1, j, target);else if (arr[m] > target)return binarySearch(arr, i, m-1, target);elsereturn m;}4.2普通二分查找
如果想了解二分查找的可以去我的这一篇,传送门
public static int binarySearchIterative(int[] arr, int target) {int left = 0;int right = arr.length - 1;while (left <= right) { // 终止条件int mid = left + (right - left) / 2; // 一般规律if (arr[mid] == target) {return mid; // 找到目标值} else if (arr[mid] < target) {left = mid + 1; // 在右半部分查找} else {right = mid - 1; // 在左半部分查找}}return -1; // 目标值未找到
}5.1递归冒泡排序
//递归冒泡排序public static void bubbleSort(int[] arr,int j) {if (j == 0) //j代表未排序区域的右边界return;int x = 0; //x代表最后一次交换的位置,可以认为是已排序区域和未排序区域的分界线for (int i = 0; i < j; i++) {if (arr[i] > arr[i+1]) {int temp = arr[i];arr[i] = arr[i+1];arr[i+1] = temp;x = i;}}bubbleSort(arr, x);}
递归冒泡排序引入变量
x的好处主要体现在以下几个方面:
减少不必要的遍历:
- 在传统的冒泡排序中,每一轮遍历都会将最大的元素“冒泡”到未排序区域的末尾。然而,在某些情况下,未排序区域的前面部分可能已经是有序的。引入
x变量后,x记录了最后一次交换的位置,这意味着从x之后的元素已经是有序的。因此,下一轮递归只需要处理到x位置,而不需要再遍历整个未排序区域,从而减少了不必要的比较和交换操作。提高效率:
- 通过减少每一轮的遍历范围,递归冒泡排序的效率得到了提升。特别是在数组接近有序的情况下,这种优化尤为明显。
简化代码逻辑:
- 引入
x变量后,代码逻辑更加清晰。x作为已排序区域和未排序区域的分界线,使得递归调用的参数更加明确,便于理解和维护。总结来说,引入
x变量使得递归冒泡排序在处理接近有序的数组时更加高效,减少了不必要的操作,提高了算法的性能。
5.2普通循环冒泡排序
public static void bubbleSortIterative(int[] arr) {int n = arr.length;for (int i = 0; i < n - 1; i++) {for (int j = 0; j < n - 1 - i; j++) {if (arr[j] > arr[j + 1]) {int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}
}递归与循环的比较
| 特性 | 递归实现 | 循环实现 |
| 可读性 | 通常更简洁,易于理解问题的结构 | 可能较冗长,但在简单情况下更直观 |
| 性能 | 可能导致栈溢出,尤其在深度递归时 | 通常更高效,避免了函数调用的开销 |
| 终止条件 | 明确的基本情况,通常是一个简单的条件 | 循环条件,通常是一个范围或计数器 |
| 一般规律 | 通过递归关系定义问题,通常简洁明了 | 通过迭代逻辑处理问题,可能需要更多的代码行 |
多路递归
以斐波那契数列为例,让我们来了解一下什么是多路递归。
斐波那契数列是一个经典的递归问题,定义如下:
F(0) = 0F(1) = 1F(n) = F(n-1) + F(n-2)对于n >= 2
单路递归
单路递归是指函数在其定义中仅调用自身一次。换句话说,函数的递归调用只有一个分支。例如,计算阶乘的递归实现就是单路递归:
public static int factorial(int n) {if (n == 0 || n == 1) return 1; // 终止条件return n * factorial(n - 1); // 单路递归调用
}多路递归
多路递归是指一个函数在递归调用时,同时调用多个子问题。在斐波那契数列的例子中,fibonacci(n) 同时调用了 fibonacci(n - 1) 和 fibonacci(n - 2),这两个调用是并行的,即它们是同时进行的。
public static int fibonacci(int n) {if (n == 0) return 0;if (n == 1) return 1;return fibonacci(n - 1) + fibonacci(n - 2);
}
多路递归的特点
并行调用:
- 在多路递归中,函数会同时调用多个子问题,这些子问题是并行进行的。
重复计算:
- 由于多个子问题可能会重复计算相同的子问题,多路递归可能会导致大量的重复计算,效率较低。例如,在计算
fibonacci(5)时,fibonacci(3)会被计算多次。空间复杂度:
- 多路递归的空间复杂度较高,因为每次递归调用都会在调用栈中占用一定的空间。

可以看到,我们计算了f(5)时已经把f(4),f(3),f(2),f(1)计算过一遍了,而我们计算f(4)时又要重新计算,这就多了许多重复的执行步骤,我们可以考虑优化一下 。
优化多路递归
为了优化多路递归,可以使用记忆化技术(Memoization)或动态规划(Dynamic Programming)来避免重复计算。例如:
public static int fibonacci(int n, int[] memo) {if (n == 0) return 0;if (n == 1) return 1;if (memo[n] != 0) return memo[n];memo[n] = fibonacci(n - 1, memo) + fibonacci(n - 2, memo);return memo[n];
}
在这个优化版本中,我们使用了一个数组 memo 来存储已经计算过的斐波那契数,从而避免了重复计算,提高了效率。


所谓记忆化就是,我们可以用一个数组来储存已经计算过的值,再次用到的时候直接拿出用即可,与没有优化前的进行对比,可以看得出分支明显减少了许多,大大提高了效率。
总结
多路递归是指一个函数在递归调用时,同时调用多个子问题。在斐波那契数列的例子中,fibonacci(n) 同时调用了 fibonacci(n - 1) 和 fibonacci(n - 2),这种并行调用的方式就是多路递归。多路递归可能会导致重复计算和较高的空间复杂度,但可以通过记忆化或动态规划来优化。
递归-爆栈问题
递归中的爆栈问题(Stack Overflow)是指在递归调用过程中,由于递归深度过大,导致调用栈(Call Stack)空间耗尽,从而引发程序崩溃或异常。
调用栈的作用
调用栈是计算机程序在执行过程中用于管理函数调用的一种数据结构。每当一个函数被调用时,系统会在调用栈中为该函数分配一块内存空间,用于存储函数的局部变量、返回地址等信息。当函数执行完毕后,这块内存空间会被释放。
递归调用的特点
在递归调用中,函数会不断地调用自身,每次调用都会在调用栈中分配一块新的内存空间。如果递归深度过大,调用栈中的内存空间会不断累积,最终可能导致调用栈空间耗尽,引发爆栈问题。
爆栈问题的示例
以计算阶乘为例:
public static int factorial(int n) {if (n == 0) return 1;return n * factorial(n - 1);
}
在这个递归函数中,factorial(n) 会调用 factorial(n - 1),factorial(n - 1) 会调用 factorial(n - 2),依此类推,直到 n 减到 0。如果 n 非常大,递归深度会非常深,调用栈的空间会迅速累积,最终可能导致爆栈问题。

可以看到数字过大时,递归调用过深,内存空间不够,会爆出异常,这就是爆栈。
爆栈问题优化-尾递归
尾递归优化(Tail Recursion Optimization)是一种针对递归函数的优化技术,它通过将递归调用转换为迭代形式,从而避免在调用栈中累积大量的内存空间,避免爆栈问题。
尾递归的特点
尾递归是指递归调用是函数的最后一个操作。换句话说,递归调用返回的结果直接作为函数的返回值,不再进行任何其他操作。
尾递归优化的原理
尾递归优化的原理是通过编译器或解释器的优化,将尾递归调用转换为迭代形式。具体来说,编译器或解释器会在编译或解释阶段,将尾递归函数转换为一个循环结构,从而避免在调用栈中累积大量的内存空间。
尾递归优化的示例
以计算阶乘为例,传统的递归实现如下:
public static int factorial(int n, int result) {if (n == 0) return result;return factorial(n - 1, n * result);
}
在这个实现中,factorial(n, result) 调用 factorial(n - 1, n * result) 后,直接返回递归调用的结果,不再进行其他操作,因此这是尾递归。
尾递归优化的效果
尾递归优化可以显著减少调用栈的使用,避免爆栈问题。具体效果如下:
减少调用栈空间:
- 由于尾递归调用是函数的最后一个操作,编译器或解释器可以将递归调用转换为迭代形式,从而避免在调用栈中累积大量的内存空间。
提高性能:
- 尾递归优化可以减少函数调用的开销,提高程序的执行效率。
避免爆栈问题:
- 尾递归优化可以有效避免递归深度过大导致的爆栈问题,提高程序的稳定性和可靠性。
支持尾递归优化的语言
并非所有编程语言都支持尾递归优化,很遗憾的是Java并不支持尾递归优化哈,以下是一些支持尾递归优化的编程语言:
- Scheme:Scheme 语言规范要求实现必须支持尾递归优化。
- Haskell:Haskell 通过惰性求值和尾递归优化来避免爆栈问题。
- Scala:Scala 编译器支持尾递归优化。
- Erlang:Erlang 虚拟机(BEAM)支持尾递归优化。
- C++:C++ 编译器通常支持尾递归优化,但这取决于具体的编译器和编译选项。尾递归优化通常是通过编译器的优化选项来实现的。
总结
爆栈问题就是由于递归调用深度过高,导致调用栈的内存空间不够用,从而引发的程序崩溃或异常。解决爆栈问题的方法包括尾递归优化、迭代替代递归和限制递归深度等。通过这些方法,可以有效避免递归中的爆栈问题,提高程序的稳定性和性能。
相关文章:

最全面的递归算法详解,一篇足矣(高手必备)
在编程中,递归和循环是两种常用的控制结构,各有其独特的优缺点。理解这两者的特点和应用场景,对于编写高效、可读的代码至关重要。 什么是递归? 递归是一种强大的编程技术,允许函数在其定义中调用自身。递归通常涉及…...
单向链表排序和双向链表操作)
数据结构(2)单向链表排序和双向链表操作
一单向链表的插入排序 void insertion_sort_link(link_t* plink) { // 如果链表头为空,直接返回 if(NULL plink->phead) { return; } // 初始化指针,p指向当前已排序部分的最后一个节点 node_t* p plink->phead; // ptemp指向待插入的…...

OpenCV结构分析与形状描述符(14)拟合直线函数fitLine()的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 拟合一条直线到2D或3D点集。 fitLine 函数通过最小化 ∑ i ρ ( r i ) \sum_i \rho(r_i) ∑iρ(ri)来拟合一条直线到2D或3D点集,…...

Mysql基础练习题 1757.可回收且低脂的产品(力扣)
编写解决方案找出既是低脂又是可回收的产品编号。 题目链接: https://leetcode.cn/problems/recyclable-and-low-fat-products/description/ 建表插入数据: Create table If Not Exists Products (product_id int, low_fats ENUM(Y, N), recyclable …...

Nginx调优,有这篇就够了
目录 1. 工作进程数量 2. Nginx最大打开文件数 3. Nginx事件处理模型 4. 开启高效传输模式 5. 连接超时时间 6. proxy调优 7. fastcgi 调优 8. gzip 调优 9. expires 缓存调优 10. 防盗链 11. 内核参数优化 1. 工作进程数量 #根据cpu个数自动调整工作进程数量 work…...
)
Java语言程序设计基础篇_编程练习题*18.17 (数组中某个指定字符出现的次数)
题目:*18.17 (数组中某个指定字符出现的次数) 编写一个递归的方法,求出数组中一个指定字符出现的次数。需要定义下面两个方法,第二个方法是一个递归的辅助方法。 public static int count(char[] chars, char ch) public static int count(…...

实时(按帧)处理的低通滤波C语言实现
写在前面: 低通滤波采用一般的FIR滤波器,因为本次任务,允许的延迟较多,或者说前面损失的信号可以较多,因此,涉及一个很高阶的FIR滤波器,信号起始段的信号点可以不处理,以及…...
Centos7.9部署Gitlab-ce-16.9
一、环境信息 软件/系统名称版本下载地址备注Centos77.9.2009https://mirrors.nju.edu.cn/centos/7.9.2009/isos/x86_64/CentOS-7-x86_64-DVD-2009.isogitlab-cegitlab-ce-16.9.1https://mirror.tuna.tsinghua.edu.cn/gitlab-ce/yum/el7/gitlab-ce-16.9.1-ce.0.el7.x86_64.rpm…...

卷积神经网络(一)
目录 一.卷积神经网络的组成 二.卷积层 目的: 参数: 计算公式 卷积运算过程 三.padding-零填充 1.Valid and Same卷积 2.奇数维度的过滤器 四.stride步长 五.多通道卷积 1.多卷积核(多个Filter) 六.卷积总结 七.池化层(Pooling) 八.全连接层…...

加密与安全_ sm-crypto 国密算法sm2、sm3和sm4的Java库
文章目录 Presm-crypto如何使用如何引入依赖 sm2获取密钥对加密解密签名验签获取椭圆曲线点 sm3sm4加密解密 Pre 加密与安全_三种方式实现基于国密非对称加密算法的加解密和签名验签 sm-crypto https://github.com/antherd/sm-crypto 国密算法sm2、sm3和sm4的java版。基于js…...

VR 尺寸美学主观评价-解决方案-现场体验研讨会报名
棣拓科技VR创新解决方案助力尺寸美学所见即所得! 诚邀各位行业专家莅临指导交流 请扫描海报二维码踊跃报名,谢谢 中国上海 2024.10.25 亮点介绍 1、通过精湛渲染技术,最真实展现设计效果,并通过VR设备一比一比例进行展现。 2、设置相关设…...

网络基础入门指南(三)
一、远程管理交换机 1.配置IP地址 远程管理需要通过IP地址访问网络设备交换机的接口,默认无法配置IP地址需要使用虚接口vlan1 2.配置远程登录密码 远程管理需要配置VTY接口VTY是虚拟终端,是一种网络设备远程连接的方式vty 0 4表示可同时打开5个会话 3…...

大众萨克森:SNP助力汽车制造智能化,实现SAP S/4HANA系统成功升级
关于大众萨克森 VW Sachsen 大众汽车(Volkswagen Sachsen GmbH)包括位于德国茨维考的汽车工厂、位于德累斯顿的透明工厂和位于开姆尼茨的发动机工厂。茨维考汽车厂拥有 7,900名员工,每天生产1,350辆高尔夫和帕萨特汽车。在开姆尼茨的发动机工…...

20240912 每日AI必读资讯
OpenAI计划在接下来的两周内发布Strawberry - 独立产品:尽管草莓是ChatGPT的一部分,但它将作为一个独立的产品发布,具体如何提供尚不清楚。它可能会出现在用户选择的AI模型下拉菜单中,与现有服务有所不同。 - 推理功能ÿ…...

Linux之Shell命令
Shell 是一个 C 语言编写的脚本语言,它是用户与 Linux 的桥梁,用户输入命令交给 Shell 处理,Shell 将相应的操作传递给内核(Kernel),内核把处理的结果输出给用户。 程序执行方式:编译、解释 Sh…...

前端Vue框架实现html页面输出pdf(html2canvas,jspdf)
代码demo: <template><el-dialog class"storageExportDialog" :fullscreen"true" title"" :visible.sync"visible" v-if"visible" width"600px"><div id"exportContainer" …...

SAP Fiori UI5-环境搭建-2022-2024界面对比
文章目录 一、Fiori项目初始化实际操作第一步:新建文件夹(项目文件)第二步:打开我们项目第三步:打开终端 部署环境第四步: XML中新增文本 二、 2023年Vscode中Fiori界面三 、2024年Vscode中Fiori界面 一、Fiori项目初始…...

二百六十三、Java——IDEA项目打成jar包,然后在Linux中运行
一、目的 在用Java对原Kafka的JSON字段解析成一条条数据,然后写入另一个Kafka中,代码写完后打成jar包,放在Linux中,直接用海豚调度运行 二、Java利用fastjson解析复杂嵌套json字符串 这一块主要是参考了这个文档,然…...

【OpenCV2.2】图像的算术与位运算(图像的加法运算、图像的减法运算、图像的融合)、OpenCV的位运算(非操作、与运算、或和异或)
1 图像的算术运算 1.1 图像的加法运算 1.2 图像的减法运算 1.3 图像的融合 2 OpenCV的位运算 2.1 非操作 2.2 与运算 2.3 或和异或 1 图像的算术运算 1.1 图像的加法运算 add opencv使用add来执行图像的加法运算 图片就是矩阵, 图片的加法运算就是矩阵的加法运算, 这就要求加…...

ChatGPT 3.5/4.0使用手册:解锁人工智能的无限潜能
1. 引言 在人工智能的浪潮中,ChatGPT以其卓越的语言理解和生成能力,成为了一个革命性的工具。它不仅仅是一个聊天机器人,更是一个能够协助我们日常工作、学习和创造的智能伙伴。随着ChatGPT 3.5和4.0版本的推出,其功能和应用范围…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...
:LSM Tree 概述)
从零手写Java版本的LSM Tree (一):LSM Tree 概述
🔥 推荐一个高质量的Java LSM Tree开源项目! https://github.com/brianxiadong/java-lsm-tree java-lsm-tree 是一个从零实现的Log-Structured Merge Tree,专为高并发写入场景设计。 核心亮点: ⚡ 极致性能:写入速度超…...
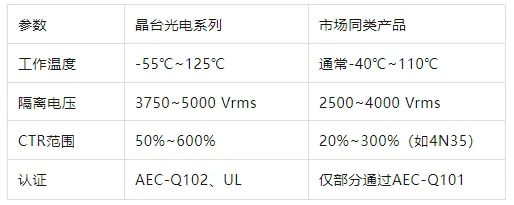
高抗扰度汽车光耦合器的特性
晶台光电推出的125℃光耦合器系列产品(包括KL357NU、KL3H7U和KL817U),专为高温环境下的汽车应用设计,具备以下核心优势和技术特点: 一、技术特性分析 高温稳定性 采用先进的LED技术和优化的IC设计,确保在…...
)
MySQL基本操作(续)
第3章:MySQL基本操作(续) 3.3 表操作 表是关系型数据库中存储数据的基本结构,由行和列组成。在MySQL中,表操作包括创建表、查看表结构、修改表和删除表等。本节将详细介绍这些操作。 3.3.1 创建表 在MySQL中&#…...
