Leetcode 最大子数组和

使用“Kadane’s Algorithm”来解决。
Kadane’s Algorithm 在每个步骤中都保持着一个局部最优解,即以当前元素为结尾的最大子数组和(也就是局部最优解),并通过比较这些局部最优解和当前的全局最优解来找到最终的全局最优解。
Kadane’s Algorithm的核心思想是:在遍历数组的过程中,动态地计算出以每个元素结尾的最大子数组和,并用一个变量来记录出现过的最大值。简单来说,它帮我们找到了一种巧妙的方式,在一次遍历中找到最大子数组的和。
通俗解释:
假设你有一个数组,比如 [-2, 1, -3, 4, -1, 2, 1, -5, 4],你想找出这个数组中和最大的子数组。Kadane’s Algorithm通过以下步骤来完成这个任务:
- 从左到右遍历数组:你会逐个看数组中的每个数字。
- 累积当前的和:对于每个数字,你有两种选择:
- 要么继续把它加到之前的子数组和里,扩展现有的子数组。
- 要么丢弃之前的子数组,从这个数字重新开始一个新的子数组。
- 更新最大和:每当你计算出一个新的子数组和时,记录下目前为止遇到的最大值。
具体的步骤如下:
-
假设一开始你的数组是
[-2, 1, -3, 4, -1, 2, 1, -5, 4],我们先从第一个数字开始。 -
第一个数字是
-2,这就是目前为止最大的子数组和,所以暂时记录为最大值。 -
接着看下一个数字
1。你现在有两个选择:- 继续加:
-2 + 1 = -1,即把1加到前面的子数组([-2])上。 - 重新开始:直接从
1开始,子数组就变成了[1]。
很显然,
1比-1大,所以你选择从1重新开始一个子数组,并更新最大和为1。 - 继续加:
-
再看下一个数字
-3,你又有两个选择:- 继续加:
1 + (-3) = -2。 - 重新开始:从
-3开始,子数组变成[-3]。
你会选择继续加,但最大和仍然保持不变为
1。 - 继续加:
-
继续这个过程,直到遍历完整个数组,每次你都比较是继续累加还是重新开始子数组,并始终记录出现过的最大子数组和。
最终,在这个例子里,你会发现最大子数组是 [4, -1, 2, 1],它的和是 6。
核心思想总结:
- Kadane’s Algorithm用一种局部最优解逐步构建出全局最优解。通过在每个位置上选择是继续累加还是重新开始子数组,你能够高效地找到整个数组的最大子数组和。
- 每次你只关心当前元素,以及前面累加的结果,这使得算法可以在**O(n)**的时间内完成问题的求解。
class Solution {
public:int maxSubArray(vector<int>& nums) {//首先利用第1个元素分别初始化局部最优解和全局最优解int current_sum = nums[0];int max_sum = nums[0];for(int i = 1; i < nums.size(); ++i) {//首先更新当前局部最优解, 对当前元素,无非2种选择:1.作为新的子数组起点,2.作为当前子数组的末尾//我们对比这两种情况的子数组和,将最大值作为局部最优解。//这行代码很巧妙,不仅更新了局部最优解,也可以设置新的子数组起点current_sum = max(nums[i], current_sum + nums[i]);//更新完局部最优解之后,紧接着和全局最优解进行对比,更新全局最优解max_sum = max(current_sum, max_sum);}return max_sum;}
};
是的,Kadane’s Algorithm**属于动态规划(Dynamic Programming,DP)**的一种具体实现。
这行代码很巧妙,不仅更新了局部最优解,也可以设置新的子数组起点
current_sum = max(nums[i], current_sum + nums[i]);
这行代码确实是Kadane’s Algorithm中最巧妙的地方,关键在于它同时做了两件事:
-
更新局部最优解:
current_sum = max(nums[i], current_sum + nums[i]);的核心在于它选择了当前子数组的最优策略。它计算了两种可能的情况:nums[i]:直接将当前元素作为新的子数组的起点,丢弃之前的累积和。current_sum + nums[i]:将当前元素加到之前已经计算出来的子数组和中,继续扩展当前子数组。
通过比较这两种情况,算法能在每个元素上做出最优决策,即决定当前子数组是否应该继续累积,还是应该重新开始。
-
自动设定新子数组起点:当
nums[i] > current_sum + nums[i]时,这意味着累加前面的子数组和反而让和变小了,因此此时就选择从nums[i]重新开始一个新的子数组。也就是说,当前元素本身就大于累积的和时,它就自然成为新的子数组的起点。这样就无需显式地去标记子数组的起点,算法通过比较自动决定何时重置。
例子解释:
以数组 [-2, 1, -3, 4, -1, 2, 1, -5, 4] 为例,我们逐步解释这行代码的行为:
- 开始时:
current_sum = -2,max_sum = -2 - 遍历到
1时:current_sum = max(1, -2 + 1) = 1,此时直接从1重新开始,max_sum更新为1。 - 遍历到
-3时:current_sum = max(-3, 1 - 3) = -2,继续累加,但max_sum保持不变。 - 遍历到
4时:current_sum = max(4, -2 + 4) = 4,重新开始一个新的子数组,max_sum更新为4。
通过这种方式,每次都能判断是扩展子数组还是从当前元素重新开始,并确保每一步都在寻找最优解。
巧妙之处总结:
- 简洁高效:通过一个简单的
max比较,Kadane’s Algorithm不仅做到了局部最优解的更新,还自动完成了子数组的起点设定。相比于需要显式地处理每个子数组的起点和终点的其他算法,Kadane’s Algorithm更加简洁、优雅。 - 避免冗余操作:无需存储额外的信息(如子数组的起点或终点),减少了空间开销,同时保持了O(n)的时间复杂度。
这就是为什么Kadane’s Algorithm被认为是一个非常经典且高效的解决最大子数组和问题的算法。
为什么Kadane’s Algorithm是动态规划?
-
重叠子问题:动态规划的核心思想之一是通过解决子问题来解决更大的问题。在Kadane’s Algorithm中,每个子数组和的最大值都依赖于前一个子数组的解。也就是说,当前位置的最优解依赖于前一个位置的最优解,这是“重叠子问题”的特性。
- 例如,在当前位置
i,我们只需要知道位置i-1处的最大子数组和,就能决定是否要把当前元素nums[i]加入到前面的子数组中,还是从当前元素重新开始。
- 例如,在当前位置
-
最优子结构:动态规划要求问题具有最优子结构,即全局问题的最优解可以由子问题的最优解构造得到。在Kadane’s Algorithm中,整个数组的最大子数组和可以通过一系列局部最大子数组和的比较来得到。
- Kadane’s Algorithm在每个步骤中都保持着一个局部最优解,即以当前元素为结尾的最大子数组和,并通过比较这些局部最优解来找到最终的全局最优解。
Kadane’s Algorithm的动态规划状态转移方程
动态规划常常有一个状态转移方程,用来更新每个子问题的最优解。Kadane’s Algorithm的状态转移方程可以表述为:
current_sum = max(nums[i], current_sum + nums[i])
这意味着:
-
对于当前的元素
nums[i],我们有两个选择:- 把它加到前面的子数组上(
current_sum + nums[i])。 - 或者,从当前元素开始一个新的子数组(
nums[i])。
这就是状态转移的过程,通过选择这两个选项中的较大值来更新
current_sum,从而实现动态规划的“状态更新”。 - 把它加到前面的子数组上(
动态规划特征总结:
- 状态:以当前位置结尾的最大子数组和(即
current_sum)。 - 状态转移方程:
current_sum = max(nums[i], current_sum + nums[i])。 - 最优解:通过遍历所有状态(即每个元素为结尾的最大子数组和),找出其中的最大值。
动态规划的优化:
Kadane’s Algorithm只需要常数空间来记录当前的子数组和以及最大子数组和,因此它是空间优化后的动态规划版本。相比于一般的动态规划需要维护一个额外的数组来保存所有子问题的解,Kadane’s Algorithm只需维护两个变量(current_sum和max_sum),这使得它的空间复杂度为O(1)。
结论:
Kadane’s Algorithm确实属于动态规划的一种,只是它通过非常高效的方式解决了最大子数组和的问题,避免了使用更多的空间来存储中间结果。
相关文章:

Leetcode 最大子数组和
使用“Kadane’s Algorithm”来解决。 Kadane’s Algorithm 在每个步骤中都保持着一个局部最优解,即以当前元素为结尾的最大子数组和(也就是局部最优解),并通过比较这些局部最优解和当前的全局最优解来找到最终的全局最优解。 Kadane’s Algorithm的核…...

目标检测-YOLOv2
YOLOv2介绍 YOLOv2(You Only Look Once version 2)是一种用于目标检测的深度学习模型,由Joseph Redmon等人于2016年提出,并详细论述在其论文《YOLO9000: Better, Faster, Stronger》中。YOLOv2在保持高速检测的同时,显…...

大数据 - OLAP与OLTP的区别
前言 联机事务处理OLTP(on-line transaction processing)和 联机分析处理OLAP(On-Line Analytical Processing)。 OLTP,主要是面向传统的“增删改查”事务系统,数据大都是以实体对象模型来存储数据&#…...

win10+eclipse+ESP8266_RTOS_SDK开发环境构建
官网教程 https://docs.espressif.com/projects/esp8266-rtos-sdk/en/latest/get-started/eclipse-setup.html 1. 导入工程 Build and Flash with Eclipse IDE — ESP8266 RTOS SDK Programming Guide documentation (espressif.com) 导入整个SDK,便于查看所有代…...

树形弹窗选择框/vue2/Element/弹框选择
前言 此类选择器根据vueelementUI实现,使用vue3的可以根据此案例稍作改动即可实现,主要功能有弹出选择、搜索过滤、搜索结果高亮等,此选择器只支持单选,如需多选可在此基础进行改造。 效果图 代码实现 使用时,props-…...

Python精选200Tips:121-125
Spend your time on self-improvement 121 Requests - 简化的 HTTP 请求处理发送 GET 请求发送 POST 请求发送 PUT 请求发送 DELETE 请求会话管理处理超时文件上传122 Beautiful Soup - 网页解析和抓取解析 HTML 和 XML 文档查找单个标签查找多个标签使用 CSS 选择器查找标签提…...

对接后端download接口报未知异常错误
你一定遇到过这种情况,在一个项目中下载功能明明好好的,下载接口调用方法与前端调用方法封装的好好的,可是换了一个接口,竟然搞罢工了,类似下面这样的,你会不会无从下手,不知道该怎么办呢&#…...

vue3 指定元素全屏 screenfull(可直接粘贴使用)
业务需求 由于输入的文字较多,需要将输入框进行全屏展示,方便输入和查看! 效果图 实现方式 下载插件"screenfull": “^6.0.2” yarn add screenfull -S项目中使用 import screenfull from "screenfull"templte中代码…...

【规范】Git Commit 约定式提交规范
文章目录 前言介绍使用约定式提交规范的好处提交信息格式信息头部(Header)正文(Body)脚注(Footer)撤销(Revert) 提交类型表格官网 前言介绍 约定式提交规范它是一种基于提交信息的轻…...
)
GDB的基本使用方法(之一)
1.编译程序 如果要让GDB调试程序,则编译生成程序时,要添加-g编译选项: $gcc -Wall -O2 -g 源文件 编译器含有针对源代码中的各种各样的错误输出信息的功能,称为警告选项。这些信息并不一定是错误,但却指出了容易引发bug的编码方式。-Werror选项可以在警告发生时,将其当…...
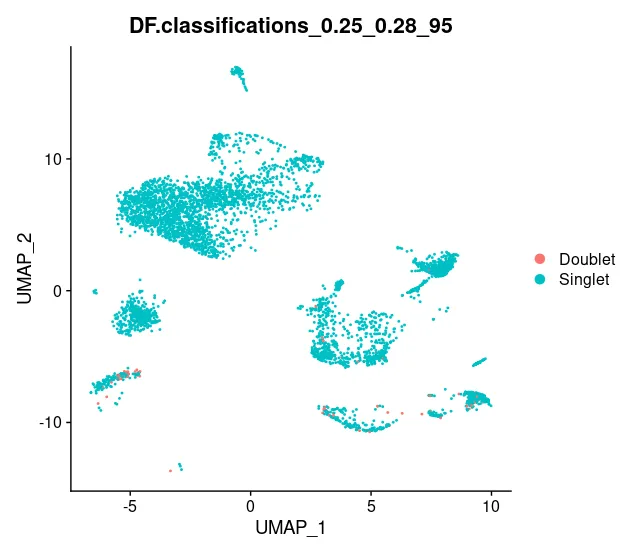
DoubletFinder去除双细胞分析学习
在单细胞RNA测序过程中,有时两个或多个细胞可能在制备过程中意外结合成一个单一的"假细胞",称为双峰细胞或双倍体。这些双峰细胞可能会扭曲数据分析和解释,因此,需要使用一些方法对它们进行识别和剔除。其中DoubletFind…...
)
软考高级第四版备考---第四十八天(项目基本要素-项目项目、项目集、项目组合和运营管理之间的关系)
一、概述: 项目集是一组相互关联且被协调管理的项目、子项目集和项目集活动,目的是为了获得分别管理无法获得的利益。项目集不是大项目,大项目是指规模、影响等特别大的项目; 项目组合是指为实现战略目标而组合在一起管理的项目、…...

系统架构设计师:信息系统基础知识
简简单单 Online zuozuo: 简简单单 Online zuozuo 简简单单 Online zuozuo 简简单单 Online zuozuo 简简单单 Online zuozuo :本心、输入输出、结果 简简单单 Online zuozuo : 文章目录 系统架构设计师:信息系统基础知识前言信息系统构成:信息系统功能:信息系统生命周期…...

微服务-nacos
nacos-注册中心 启动 服务注册到nacos...

快速上手 | 数据可观测性平台 Datavines 自定义SQL规则使用指南
摘要 本文主要介绍在 Datavines平台已有规则不能满足需求的情况下,如何通过自定义SQL规则来实现基于业务特性的数据质量检查。 规则介绍 自定义聚合SQL规则是 Datavines 平台中内置的一个灵活的规则,该规则允许用户通过编写SQL的方式来实现想要的数据质…...

MySQL零基础入门教程-6 查询去重、内外连接查询、子查询、分页查询DQL,基础+实战
教程来源:B站视频BV1Vy4y1z7EX 001-数据库概述_哔哩哔哩_bilibili 我听课收集整理的课程的完整笔记,供大家学习交流下载:夸克网盘分享 本文内容为完整笔记的第六篇 分组查询&DQL总结P41-P66 1、把查询结果去除重复记录 注意…...

Elastic:如何将数据转化为可操作的见解?
作者:来自 Elastic Elastic Platform Team 一切,从某种程度上说,每个人,都是数据。在我们这个数据驱动的世界里,我们的兴趣和互动被统计和分类,为组织提供如何创造更好的产品和更好的体验的见解。更不用说&…...

基于SSM和VUE的药品管理系统(含源码+sql+视频导入教程+文档)
👉文末查看项目功能视频演示获取源码sql脚本视频导入教程视频 1 、功能描述 基于SSM和VUE的药品管理系统2拥有两种角色 管理员:药品管理、出库管理、入库管理、销售员管理、报损管理等 销售员:登录注册、入库、出库、销售、报损等 1.1 背景…...

机器学习--神经网络
神经网络 计算 神经网络非常简单,举个例子就理解了(最后一层的那个写错了,应该是 a 1 ( 3 ) a^{(3)}_1 a1(3)): n o t a t i o n notation notation: a j ( i ) a^{(i)}_j aj(i) 表示第 i i i 层的…...

post请求中有[]报400异常
序言 在和前端同学联调的时候,发现只要post请求参数里面有[],就会报400的错误 可以看到日志中: The valid characters are defined in RFC 7230 and RFC 3986 解决办法: 参考了博客: spring boot 中解决post请求中有…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...
