线性代数 第七讲 二次型_标准型_规范型_坐标变换_合同_正定二次型详细讲解_重难点题型总结
文章目录
- 1.二次型
- 1.1 二次型、标准型、规范型、正负惯性指数、二次型的秩
- 1.2 坐标变换
- 1.3 合同
- 1.4 正交变换化为标准型
- 2.二次型的主要定理
- 3.正定二次型与正定矩阵
- 4.重难点题型总结
- 4.1 配方法将二次型化为标准型
- 4.2 正交变换法将二次型化为标准型
- 4.3 规范型确定取值范围问题
- 4.4 已知两个二次型f和g,求正否能通过正交变换使得f转换为g
- 4.5 由已知条件,反求二次型f(x~1~,x~2~....)的表达式(反求矩阵问题)
1.二次型
1.1 二次型、标准型、规范型、正负惯性指数、二次型的秩
二次型:
二次型中的矩阵A是实对称矩阵,实对称矩阵天然的可相似对角化。

解释说明:
二次型其实是一个由二次的项组成的式子
它可以写成XTAX的形式,其中A矩阵是对称阵
其中A矩阵是怎么写出来的?
1.A的对角线元素是由xn的平方决定,a11是x12前的系数,a22是x22前的系数,以此类推
2. 对称位置a12,a21 这种由混合项x1x2的系数决定,以此类推
标准型:

解释说明:
标准型就是去掉了混合项,二次型矩阵A变成了对角矩阵
注意:一个二次型的标准型并不唯一,在选择题中,我们求出的标准型和答案给出的标准型不一定一样,但是正负项数肯定一样,即规范型一样。
规范型:
规范型就是在标准型的基础上,平方项的次数是1或-1或0
规范型能确定什么?
不同的标准型能被化成相同的规范型的形式。
所以说,规范型能确定的东西有限,我们只能通过规范型得到正负系数,正负惯性指数
正惯性指数 负惯性指数:

解释说明:
正惯性指数就是标准型中平方项系数为正数的个数
负惯性指数就是标准型中平方项系数为负数的个数
正惯性指数 负惯性指数是对标准型而言的,只有处理成标准型才能看见正负惯性指数
二次型的秩:
二次型的秩就是二次型矩阵A的秩
r(f)=r(A)
1.2 坐标变换
坐标变换,其实我们可以理解为换元,在高等数学的学习中,我们经常利用换元法将复杂的式子通过换元来变成简单的式子,在二次型中也同样如此,
x=Cy的形式换元,重要的是C矩阵 |C|≠0

1.3 合同
如CTAC=B,C可逆,称矩阵A和B合同
合同的性质:
- A合同于A
- A合同于B,则B合同于A
- 合同具有传递性,A合同于B,B合同于C,A合同于C
二次型与正交变换与合同之间的联系:

补充:通过坐标变换,可以得到A合同于一个对角矩阵
1.4 正交变换化为标准型
核心:通过求二次型矩阵A的特征值,就可得出二次型的标准型。通过求二次型矩阵A的特征向量,得到坐标变换x=Qy,其中Q是由A的特征向量经过施密特正交化组成的。

二次型化标准型就转变成了求特征值求特征向量的问题。
2.二次型的主要定理
定理1:
见二次型与正交变换与合同之间的联系的结论
定理2:
任一个二次型XTAX都存在坐标变换x=cy化成标准型
3.正定二次型与正定矩阵
n元二次型f(x1,x2…)=xTAx,若对任意的x[x1,x2,…,xn]T≠0,均有xTAx>0,则称f为正定二次型,A为正定矩阵。
正定二次型的充要条件:
1.定义法 任意x, xTAx>0
2.f的正惯性指数p=n
3.A的特征值λi均>0
4.A的全部顺序主子式均>0
正定二次型的必要条件:
1.aii>0
2.|A|>0
在判断是否是正定矩阵的题目中,常用充要条件是2-4或必要条件1得出
补充一个小知识:反对称矩阵AT=-A
4.重难点题型总结
4.1 配方法将二次型化为标准型
配方法将含有平方项的二次型化为标准型:
一步一步来,先配x1,再配x2,这样就能防止|c|=0,使得坐标变换失败

题目来源:李永乐线代辅导讲义 例 6.4
配方法将不含有平方项的二次型化为标准型:

题目来源:李永乐线代辅导讲义 例 6.5
4.2 正交变换法将二次型化为标准型
在写出二次型矩阵出过程中,非常值得注意的是平方项不用除以2,混合项除以2

题目来源:李永乐线代辅导讲义 例 6.6-6.7
4.3 规范型确定取值范围问题

4.4 已知两个二次型f和g,求正否能通过正交变换使得f转换为g
思路:
相似的传递性 合同的传递性
f相似且合同于一个对角阵,g也相似且合同于一个对角阵,他俩相似且合同的对角阵是同一个对角阵,那么f与g相似且合同,所以必有一个正交变换能使得f可以变成g。
综上本质就是,f和g有相同的特征值
一些细节:x=Q1z 得到对角阵,y=Q

题目来源:李永乐线代辅导讲义 例 6.9
4.5 由已知条件,反求二次型f(x1,x2…)的表达式(反求矩阵问题)
思路如下:
求二次型表达式,也就是求二次型矩阵A,也就是方程组应用那节中的反求矩阵问题,反求矩阵问题两大核心利器,一是矩阵乘法,二是相似

题目来源:李永乐线代辅导讲义 例 6.13
相关文章:

线性代数 第七讲 二次型_标准型_规范型_坐标变换_合同_正定二次型详细讲解_重难点题型总结
文章目录 1.二次型1.1 二次型、标准型、规范型、正负惯性指数、二次型的秩1.2 坐标变换1.3 合同1.4 正交变换化为标准型 2.二次型的主要定理3.正定二次型与正定矩阵4.重难点题型总结4.1 配方法将二次型化为标准型4.2 正交变换法将二次型化为标准型4.3 规范型确定取值范围问题4.…...

国内外网络安全政策动态(2024年8月)
▶︎ 1.《关于进一步加强智能网联汽车准入、召回及软件在线升级管理的通知》公开征求意见 8月1日,工业和信息化部装备工业一司联合市场监管总局质量发展局组织编制了《关于进一步加强智能网联汽车准入、召回及软件在线升级管理的通知(征求意见稿&#…...
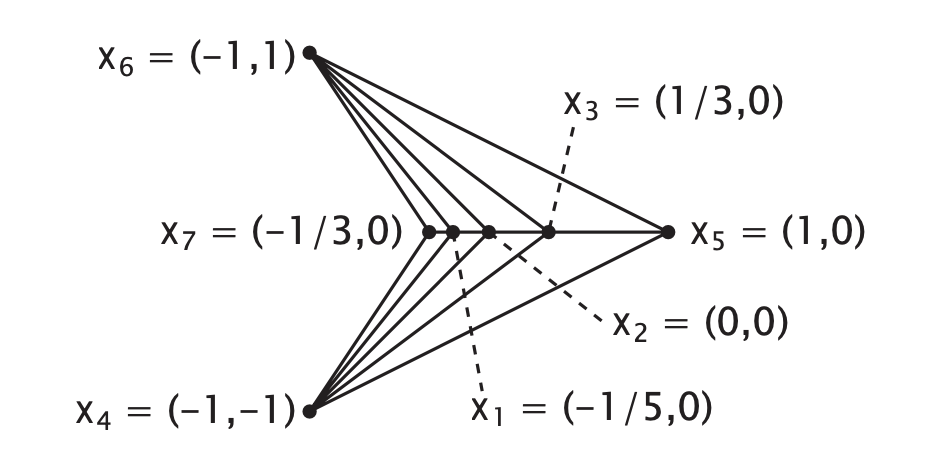
重心映射:坐标系统与边界处理策略
重心映射 在许多应用中,特别是在计算机图形学中,现在通常使用三角形网格形式的分段线性曲面工作,在本课程笔记的剩余部分,我们将主要坚持使用这种类型的曲面。 3.1 三角形网格 如前一章所述,让我们用 $ p (x,y,z) $ …...

python-网页自动化(二)
获取元素属性 1. 获取属性 以百度首页的logo为例,获取logo相关属性 <img hidefocus"true" id"s_lg_img" class"index-logo-src" src"//www.baidu.com/img/PCtm_d9c8750bed0b3c7d089fa7d55720d6cf.png" width"270…...

QT实战 商城客户端开发
需要qt先配置mysql cmake编译 一共2个文件 第一个导入数据库,mysql数据库密码在main.cpp里修改成你自己的,然后打开导入即可 第二个是客户端,mysql数据库密码在BasicWindow.cpp里修改成你自己的...
使用Java增删改查数据库
文章目录 前言一、PrepareStatement类是什么?二、实操展示 1.增2.删3.改4.查总结 前言 既然连接数据库都可以通过java语言实现,那么通过java语言对数据库进行增删改查的操作自然是顺理成章的事情了。 一、PrepareStatement类是什么? PrepareS…...
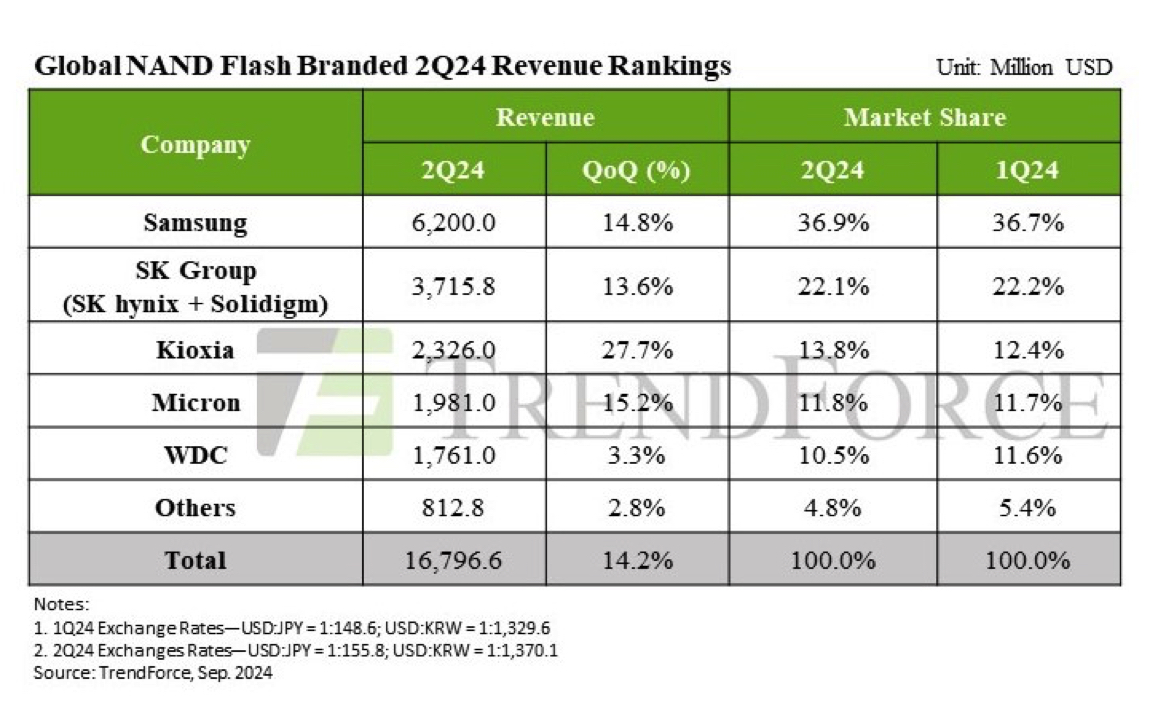
NAND发货量增长放缓,2024 Q2营收增长14%
根据市场研究机构TrendForce Corp.于2024年9月9日发布的报告,2024年第二季度NAND闪存发货量增长放缓,但营收增长了14%,主要受人工智能(AI)固态硬盘(SSD)需求的推动。 NAND闪存市场概况 2024年…...

2024年9月13日 十二生肖 今日运势
小运播报:2024年9月13日,星期五,农历八月十一 (甲辰年癸酉月庚辰日),法定工作日。 红榜生肖:猴、鼠、鸡 需要注意:牛、兔、狗 喜神方位:西北方 财神方位:…...
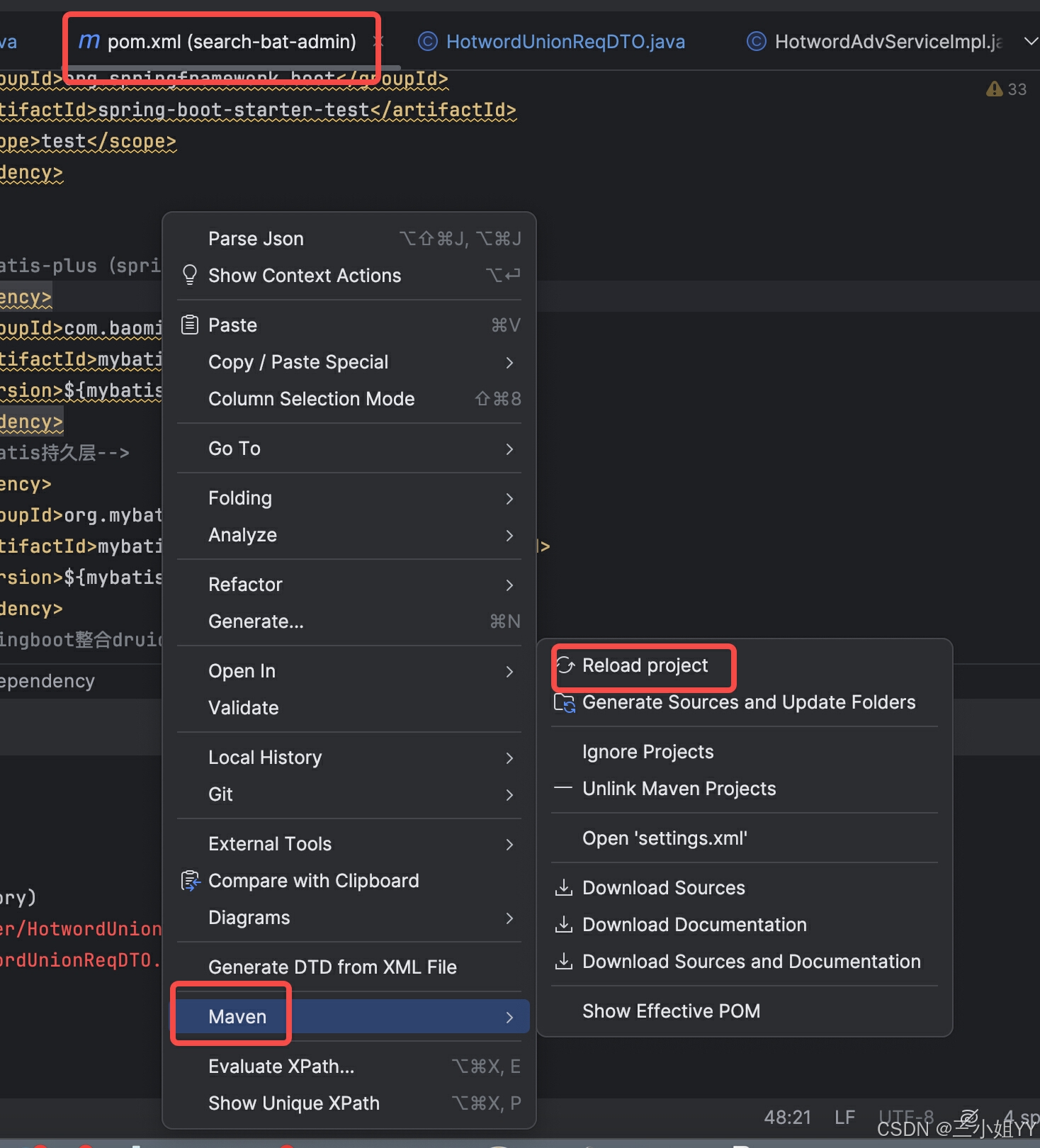
Maven 常见问题以及常用命令
常见问题 : 1. 识别不了maven项目 mvn clean install -Dmaven.test.skiptrue //构建 2. 打jar包时报异常 指定下jdk版本 常用命令: mvn clean mvn package mvn install mvn deploy...

自定义分区
通过简单例子了解partition分区类的重写方法 分区是在MR的过程中进行的,属于Shuffle阶段 但是在Job端不要忘记进行调用:job.setPartitionerClass(xxx.class) 按照年龄分区: class AgePartitioner extends Partitioner<MyComparable, N…...
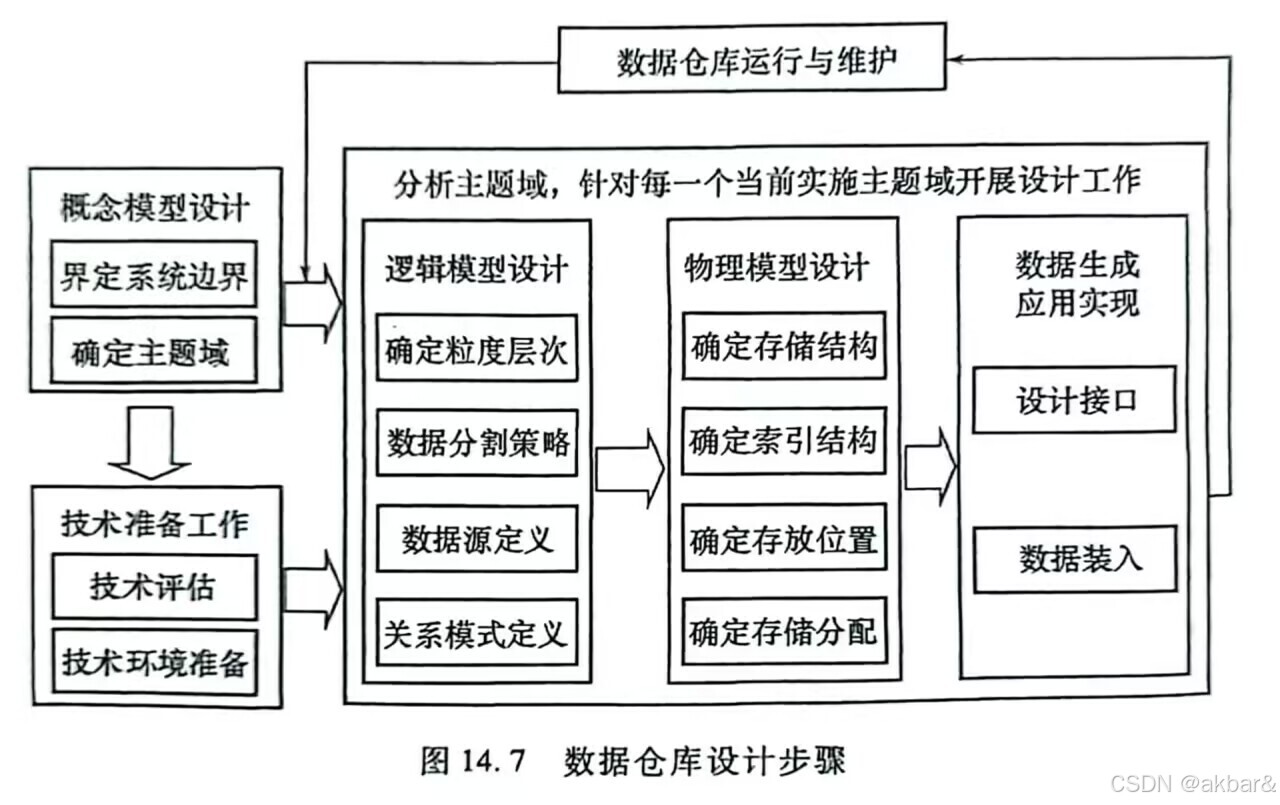
计算机三级 - 数据库技术 - 第十四章 数据仓库与数据挖掘 笔记
第十四章 数据仓库与数据挖掘 内容提要: 了解数据仓库相关技术了解数据仓库的设计、建造、运行及维护了解OLAP及多维数据模型了解数据挖掘技术 决策支持系统(DSS):综合利用大量数据有机组合众多模型(数学模型和数据处理模型),通过人机交互&a…...

低代码移动端集成:简化开发、提升用户体验的利器
什么是低代码平台? 低代码平台是一种开发工具,它允许用户通过图形化界面而非传统编程语言来构建应用程序。这种平台通过可视化的拖拽组件和配置,显著简化了应用开发过程。用户可以在这些平台上快速创建功能模块、设计用户界面,并…...
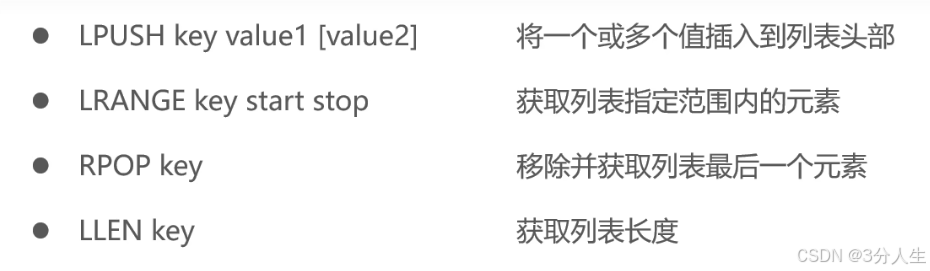
Redis入门1
Redis简介 Redis是一个基于内存的 key-value 结构数据库。 基于内存存储,读写性能高 适合存储热点数据(热点商品、资讯、新闻) 企业应用广泛 官网:https://redis.io 中文网:https://www.redis.net.cn/ window版启动命令 redis-server.exe redis.windows.con…...

SHT20温湿度传感器的C语言驱动
SHT20 是一款高精度的温湿度传感器,常用于环境监测和自动化控制系统中。以下是 SHT20 温湿度传感器的 C 语言驱动示例,展示了如何通过 I2C 通信与 SHT20 传感器进行通信以获取温度和湿度数据。 驱动流程 初始化 I2C 通信发送命令读取温度或湿度数据解析…...
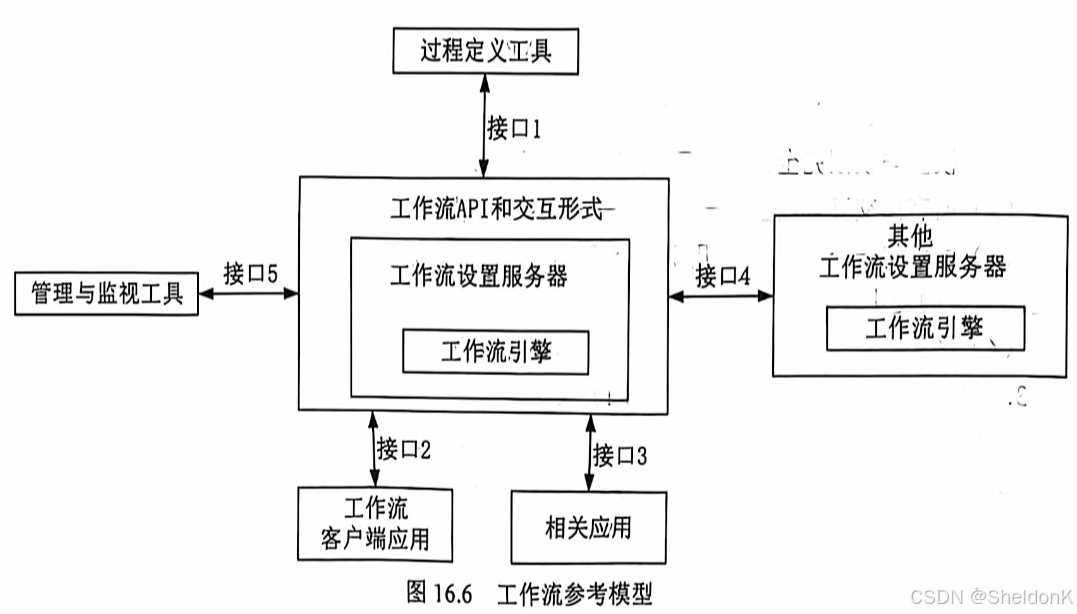
系统架构师考试学习笔记第四篇——架构设计实践知识(16)层次式架构设计理论与实践
本章考点: 大纲,本课时知识点会涉及单选为题型(约占2~5分)和案例题(25分),本课时内容偏重于方法的掌握和应用,根据以往全国计算机技术与软件专业技术资格(水平)考试的出题规律,概念知识的考查内容多数来源于实际应用,还需要灵活运用相关知识点。本课时知识架构如图1…...
顶踩Emlog插件源码
源码介绍 顶踩Emlog插件源码 前些天看到小刀娱乐网的文章页面有了一些变化,那就是增加了一个有价值/无价值的顶踩按钮。 样式也是非常的好看 再加上两个表情包是非常的有趣。 写到了Emlog系统,效果如上图。 如何使用: 需要在echo_log.…...

国庆出游季,南卡Runner Pro5骨传导耳机让旅途更完美!
国庆长假将至,无论是计划一场远行还是近郊的户外活动,一款适合的耳机都能让旅途更加愉快。南卡Runner Pro5骨传导耳机以其独特的设计和功能,成为了国庆出行的理想伴侣。 首先,骨传导耳机通过颅骨传递声音,避免了传统耳…...
)
HarmonyOS NEXT 封装实现好用的网络模块(基于最新5.0的API12)
在 HarmonyOS-NEXT 开发中,网络请求是应用开发中不可或缺的一部分。为了提高开发效率和代码复用性,我们可以封装一个好用的网络模块组件。本文将介绍如何在 HarmonyOS-NEXT 中封装一个功能强大且易于使用的网络模块组件。 封装目的 网络模块使用的频率最…...
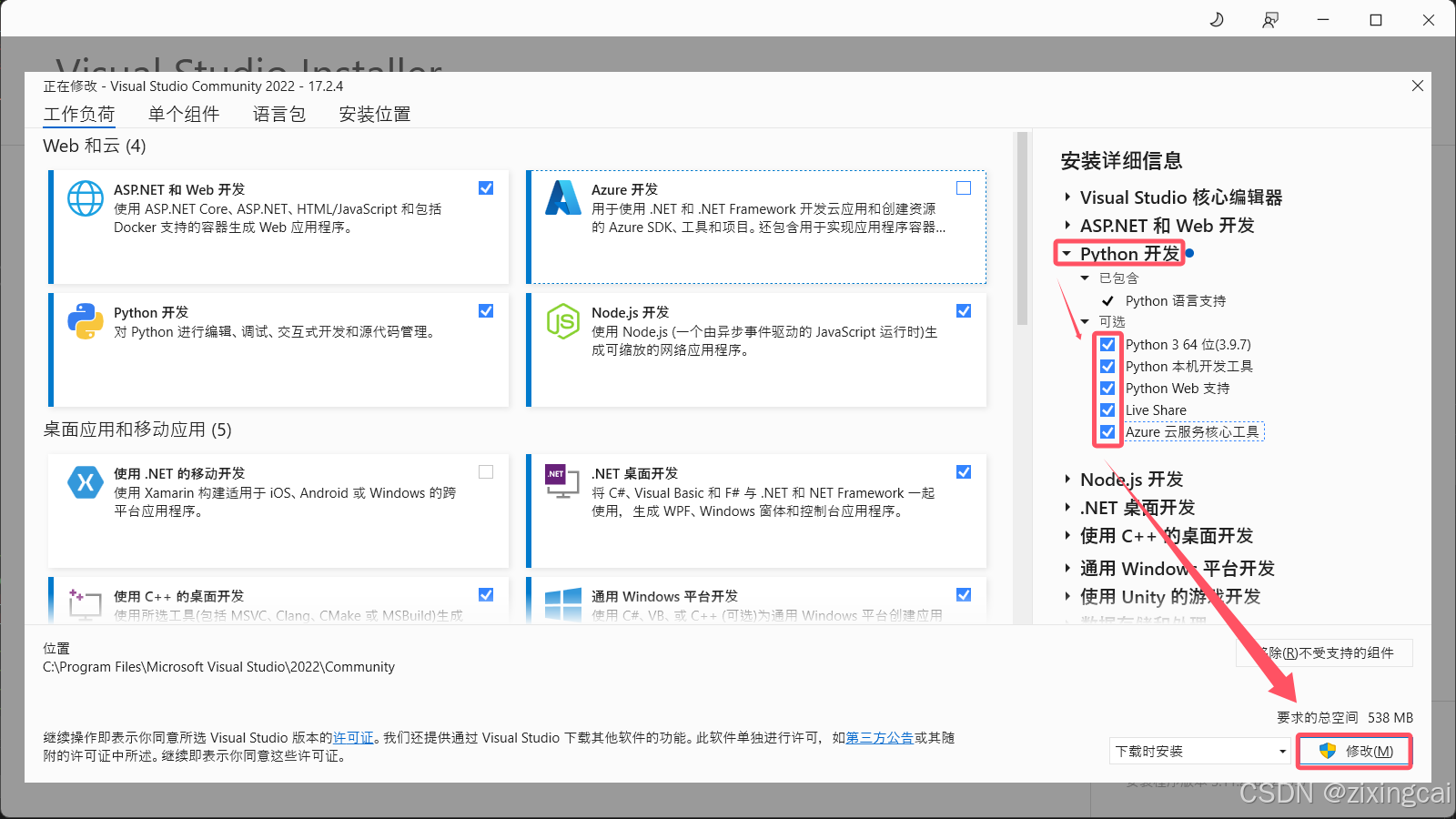
Visual Studio提示:无法安装CPpython.Exe.x64
如果你需要在Visual Studio中使用python环境,而且你本身已经有一个python环境,则只需要将你自己的python环境配置到Visual Studio中即可,可以无视如题报错,将不会产生实质性的问题或影响。 解决办法: 工具->获取工…...
计算机网络 ---- 电路交换、报文交换、分组交换
目录 零、前言 一、计算机网络发展初期面临的问题 1.1 电路交换的主要特点【电话网络采用电路交换技术】 1.1.1 电路交换的基本知识介绍 1.1.2 电路交换的优缺点 1.3 报文交换技术的特点【电报网络采用报文交换技术】 1.3.1 报文交换的基本知识介绍 1.3.2 报文交换技术…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

python打卡第47天
昨天代码中注意力热图的部分顺移至今天 知识点回顾: 热力图 作业:对比不同卷积层热图可视化的结果 def visualize_attention_map(model, test_loader, device, class_names, num_samples3):"""可视化模型的注意力热力图,展示模…...
多模态学习路线(2)——DL基础系列
目录 前言 一、归一化 1. Layer Normalization (LN) 2. Batch Normalization (BN) 3. Instance Normalization (IN) 4. Group Normalization (GN) 5. Root Mean Square Normalization(RMSNorm) 二、激活函数 1. Sigmoid激活函数(二分类&…...

Python打卡训练营学习记录Day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

