Python 求亲和数
亲和数(Amicable Numbers)是指两个不同的正整数,它们的真因数(即除去本身的所有因数)之和与对方的数相等。

def sum_of_proper_divisors(n):"""计算一个数的真因子之和"""divisors_sum = 1 # 1 是所有正整数的因子for i in range(2, int(n**0.5) + 1):if n % i == 0:divisors_sum += iif i != n // i:divisors_sum += n // ireturn divisors_sumdef find_amicable_pairs(limit):"""查找所有两个整数都小于给定上限的亲和对"""amicable_pairs = []for num in range(2, limit):partner = sum_of_proper_divisors(num)if partner > num and partner < limit and sum_of_proper_divisors(partner) == num:amicable_pairs.append((num, partner))return amicable_pairsif __name__ == "__main__":limit = 10000amicable_pairs = find_amicable_pairs(limit)print(f"All amicable pairs below {limit}:")for pair in amicable_pairs:print(pair)
All amicable pairs below 10000:
(220, 284)
(1184, 1210)
(2620, 2924)
(5020, 5564)
(6232, 6368)
相关文章:

Python 求亲和数
亲和数(Amicable Numbers)是指两个不同的正整数,它们的真因数(即除去本身的所有因数)之和与对方的数相等。 def sum_of_proper_divisors(n):"""计算一个数的真因子之和"""divisors_su…...

【C++】——vector模拟实现和迭代器失效问题
文章目录 模拟实现vector基本成员变量vector的构造与析构vector迭代器vector容量vector元素访问vector修改操作 vector迭代器失效问题什么是迭代器失效1.插入元素导致迭代器失效2.删除元素导致迭代器失效3.重新分配空间导致迭代器失效 如何解决迭代器失效问题 模拟实现 vector…...

USB 3.1 标准 A 型连接器及其引脚分配
USB 3.1 标准 A 型连接器 USB 3.1 标准 A 型连接器被定义为主机连接器。它具有与 USB 2.0 标准 A 型连接器相同的配合接口,但增加了另外两对差分信号和一个接地引脚。 USB 3.1 标准 A 型插座可以接受 USB 3.1 标准 A 型插头或 USB 2.0 标准 A 型插头。类似地&…...

机器学习文献|基于循环细胞因子特征,通过机器学习算法预测NSCLC免疫治疗结局
今天我们一起学习一篇最近发表在Journal for immunotherapy of cancer (IF 10.9)上的文章,Machine learning for prediction of immunotherapeutic outcome in non-small-cell lung cancer based on circulating cytokine signatures[基于循环…...

Qt 实现自定义截图工具
目录 Qt 实现自定义截图工具实现效果图PrintScreen 类介绍PrintScreen 类的主要特性 逐步实现第一步:类定义第二步:初始化截图窗口第三步:处理鼠标事件第四步:计算截图区域第五步:捕获和保存图像 完整代码PrintScreen.…...

第15-05章:获取运行时类的完整结构
我的后端学习大纲 我的Java学习大纲 6.1.第一组方法API: 1.API列表:java.lang.Class 类: 2.代码测试: public class ReflectionUtils{ puvblic static void main(String[] args){}// 第一组Testpublic void api_01{//上面截图的代码......…...

【Kubernetes】K8s 的鉴权管理(二):基于属性 / 节点 / Webhook 的访问控制
K8s 的鉴权管理(二):基于属性 / 节点 / Webhook 的访问控制 1.基于属性的访问控制(ABAC 鉴权)2.基于节点的访问控制(node 鉴权)2.1 读取操作2.2 写入操作 3.基于 Webhook 的访问控制3.1 基于 We…...

Java面试、技巧、问题、回复,资源面面观
入门 先了解一下面试流程 复习 Java 基础知识: 温习 Java 编程的核心概念,包括数据类型、变量、循环、数组和面向对象的编程原则。数据结构和算法: 加强您对 Java 编程中使用的基本数据结构和算法的理解。练习编码: 在各种平台上解…...

深入理解Elasticsearch的`_source`字段与索引优化
在Elasticsearch (ES) 中,_source字段是一个关键组件,它不仅决定了数据的存储方式,还影响到查询时返回的内容。在某些场景下,我们可以通过配置_source来优化存储和性能,尤其是当我们希望减少存储空间或避免返回某些字段…...
Pikachu靶场
先来点鸡汤,少就是多,慢就是快。 环境搭建 攻击机kali 192.168.146.140 靶机win7 192.168.146.161 下载zip,pikachu - GitCode 把下载好的pikachu-master,拖进win7,用phpstudy打开网站根目录,.....再用…...

TS axios封装
方式一 service/request/request.ts import axios from axios import { ElLoading } from element-plus import type { AxiosRequestConfig, AxiosInstance, AxiosResponse } from axios import type { ILoadingInstance } from element-plus/lib/el-loading/src/loading.typ…...

学会使用西门子博途Startdrive中的测量功能
工程师在驱动调试过程中,往往需要对驱动系统的性能进行分析及优化,比如说借助于调试软件中的驱动器测量功能,可以得到驱动系统的阶跃响应、波特图等,以此为依据工程师可以调整速度控制器、电流控制器的相关参数,使驱动…...
Spring Security认证与授权
1 Spring Security介绍 Spring Security是一个能够为基于Spring的企业应用系统提供声明式的安全访问控制解决方案的安全框架。由于它是Spring生态系统中的一员,因此它伴随着整个Spring生态系统不断修正、升级,在spring boot项目中加入springsecurity更是…...
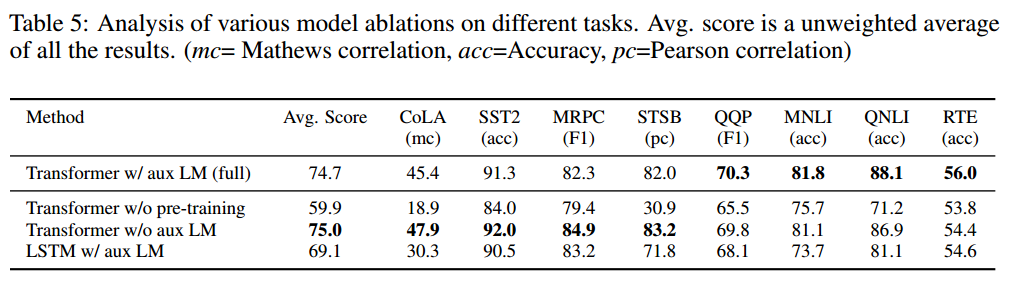
速通GPT:Improving Language Understanding by Generative Pre-Training全文解读
文章目录 速通GPT系列几个重要概念1、微调的具体做法2、任务感知输入变换3、判别式训练模型 Abstract概括分析和观点1. 自然语言理解中的数据问题2. 生成预训练和监督微调的结合3. 任务感知输入变换4. 模型的强大性能 Introduction概括分析和观点1. 自然语言理解的挑战在于对标…...
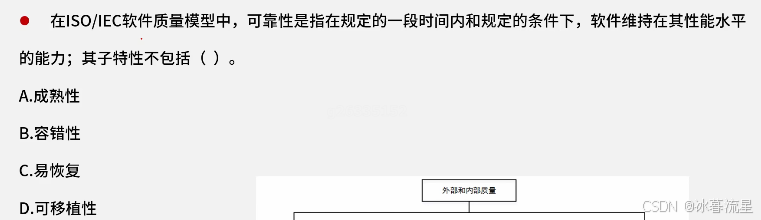
软件质量保证例题
答案:D 软件质量保证 功能性 适合性 准确性 互操作性 安全保密性 依从性 可靠性 成熟性 容错性 易恢复性 易用性 易理解性 易学性 易操作性 效率 时间特性 资源利用性 维护性 易分析性 易改变性 稳定性 易测试性 可移植性 适应性 易安装性 一致性 易替换…...
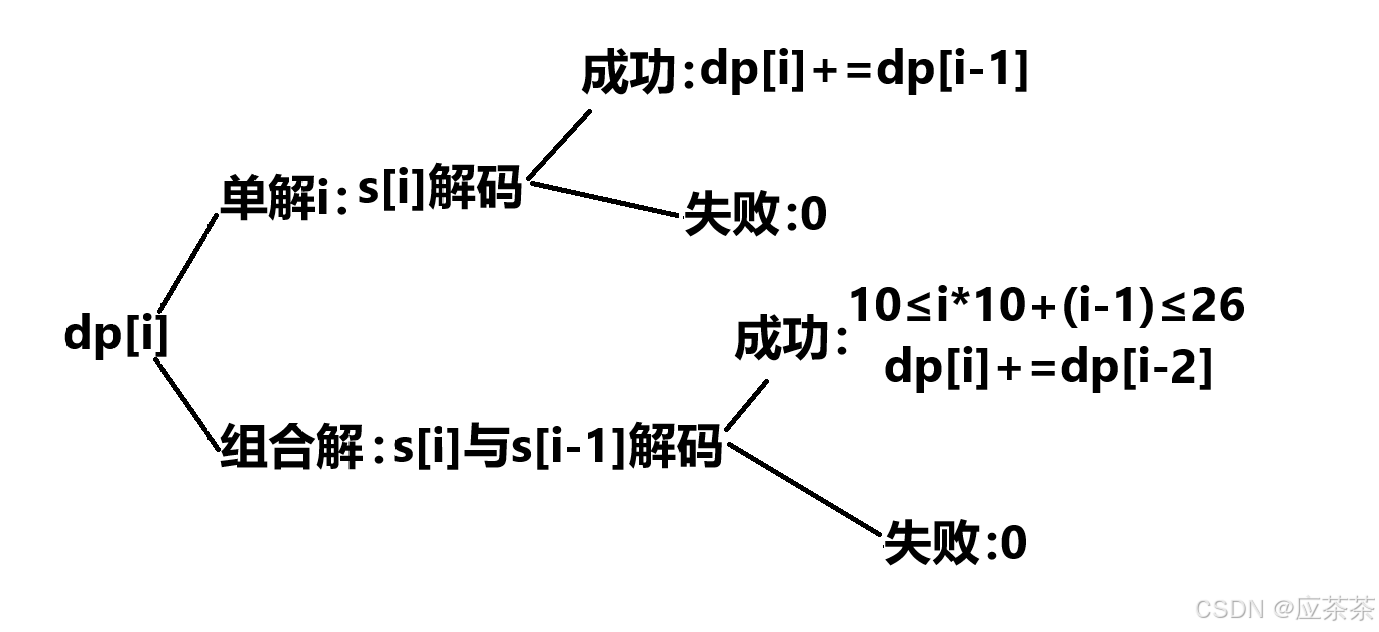
动态规划算法---04.斐波那契数列模型_解码方法_C++
题目链接:91. 解码方法 - 力扣(LeetCode)https://leetcode.cn/problems/decode-ways/description/ 一、题目解析 题目: 题目大意:从题目中我们可以知道,解码就是在字符串s中由‘1’到‘26’的字符可以转化…...

crm如何做私域运营?
流量获取的挑战日益增加,客户线索成本高、客户资源流失严重、转化率低,因此,私域流量管理已成为关键。 当前挑战 1、公域流量难以整合:外部流量分散,难以有效汇总和沉淀。 2、私域运营体系缺失:缺乏有效沟…...
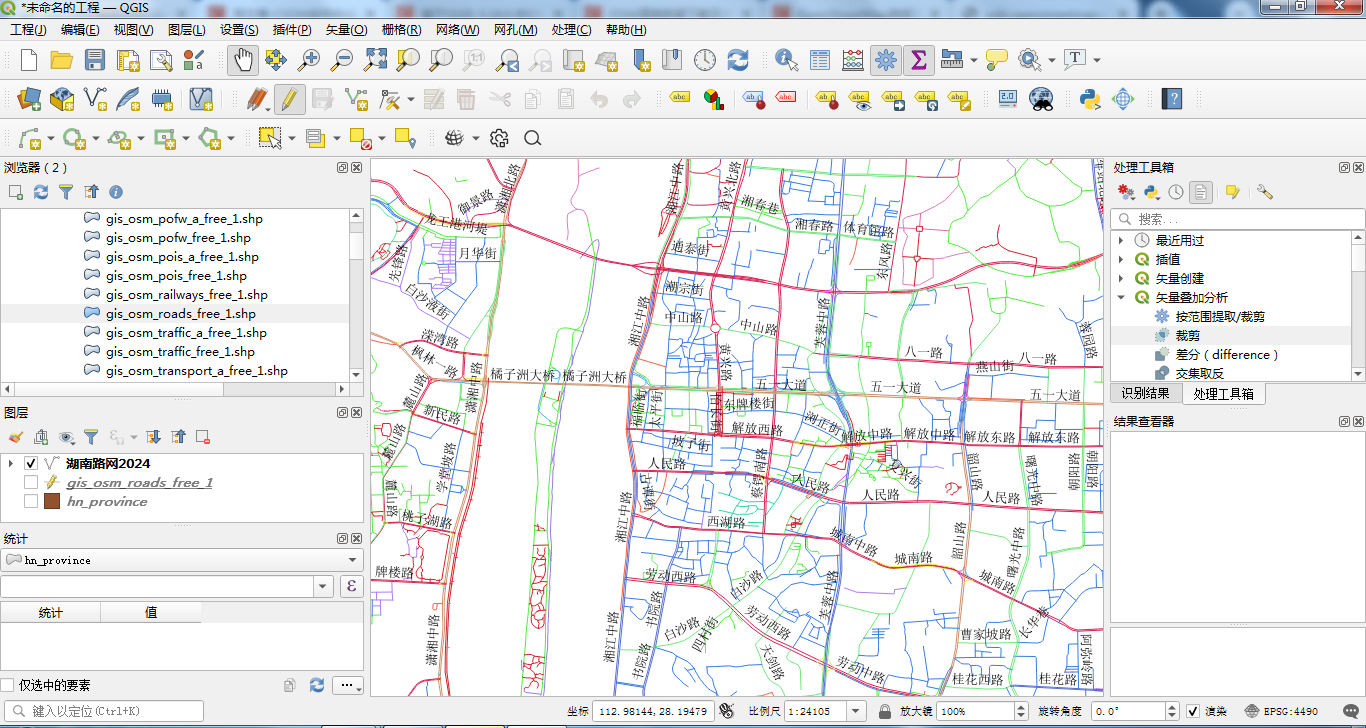
基于QGIS 3.16.0 的OSM路网矢量范围裁剪实战-以湖南省为例
目录 前言 一、相关数据介绍 1、OMS路网数据 2、路网数据 3、路网图层属性 二、按省域范围进行路网裁剪 1、裁剪范围制定 2、空间裁剪 3、裁剪结果 三、总结 前言 改革开放特别是党的十八大以来,我国公路发展取得了举世瞩目的成就。国家高速公路网由“7 射…...
WPF 手撸插件 八 依赖注入
本文内容大量参考了:https://www.cnblogs.com/Chary/p/11351457.html 而且这篇文章总结的非常好。 1、注意想使用Autofac,Autofac是一个轻量级、高性能的依赖注入(DI)框架,主要用于.NET应用程序的组件解耦和…...

走进低代码报表开发(一):探秘报表数据源
在前文当中,我们对勤研低代码平台的流程设计功能进行了介绍。接下来,让我们一同深入了解在企业日常运营中另一个极为常见的报表功能。在当今数字化时代,高效的报表生成对于企业的决策至关重要。勤研低代码开发平台能够以卓越的性能和便捷的操…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...
