判断当前用户登录时常是否超过两个小时
有一个签到功能需要用户登录时间超过两个小时才可以签到
1. 存储登录时间戳
login() { // 假设这是登录后的操作 const currentTime = new Date().getTime(); // 获取当前时间戳 localStorage.setItem('loginTimestamp', currentTime.toString()); // 存储登录时间戳 // 其他登录后的操作...
}2. 检查登录时间是否超过两个小时
封装一个函数
isLoggedInMoreThanTwoHours() { const loginTimestamp = parseInt(localStorage.getItem('loginTimestamp')) || 0; // 获取登录时间戳 const currentTimestamp = new Date().getTime(); // 获取当前时间戳 const twoHoursInMilliseconds = 2 * 60 * 60 * 1000; // 两个小时的毫秒数 // 如果登录时间戳存在且当前时间与登录时间之差大于两个小时 if (loginTimestamp && (currentTimestamp - loginTimestamp > twoHoursInMilliseconds)) { return true; // 超过两个小时 } return false; // 未超过两个小时
}3. 使用这个函数
checkLoginTime() { if (this.isLoggedInMoreThanTwoHours()) { alert('您的登录时间已超过两个小时,请重新登录!'); // 执行重新登录或其他操作 } else { console.log('您的登录时间未超过两个小时。'); } },相关文章:

判断当前用户登录时常是否超过两个小时
有一个签到功能需要用户登录时间超过两个小时才可以签到 1. 存储登录时间戳 login() { // 假设这是登录后的操作 const currentTime new Date().getTime(); // 获取当前时间戳 localStorage.setItem(loginTimestamp, currentTime.toString()); // 存储登录时间戳 // 其他…...

nacos明明配置了远程连接地址却一直连接本地的详细配置解释
大家时间都很珍贵,我直接把方法放这 这个是yml文件,我们配置yml文件的时候,一定要把他的服务发现地址写了 这里是针对bootstrap做出的文件,注意名字,要和我们在yml文件里面的spring名字一样 yml discovery:是发现的意…...

Superset二次开发之源码 run-server.sh 分析
背景: 如果基于docker方式部署Superset项目,Dockerfile文件末尾指向了docker-ci.sh,而docker-ci.sh 脚本又指向了run-server.sh。因此我们重点分析一下run-server脚本 路径 docker\run-server.sh #!/usr/bin/env bashHYPHEN_SYMBOL-gunicorn…...

Java 之四种内部类详解
在 Java 中,除了传统的类定义方式之外,还有一种特殊的类定义方式——内部类。内部类定义在另一个类的内部,可以访问外部类的成员,这使得代码更加灵活和可读性更强。本文将详细讲解 Java 中四种内部类的类型:成员内部类…...

03:手动可变电阻
可变电阻 1、电位器2、变阻器/数字电位器2.1:变阻器2.2:数字电位器 3、电位器锥度4、寄生电感/电容 1、电位器 如上图所示:将可变的电阻作为分压器,那么这种可变的电阻就是电位器。例如:将L1连接负极,L3连接…...
)
嵌入式Linux电池管理(TODO)
(TODO) 在树莓派3B上使用电池供电需要考虑多个方面,包括电源管理、硬件连接和软件配置。以下是详细的步骤和建议: 1. 选择合适的电池 树莓派3B需要5V的电源供电,通常电流需求在2.5A左右。常见的电池选择包括࿱…...

Python 求亲和数
亲和数(Amicable Numbers)是指两个不同的正整数,它们的真因数(即除去本身的所有因数)之和与对方的数相等。 def sum_of_proper_divisors(n):"""计算一个数的真因子之和"""divisors_su…...

【C++】——vector模拟实现和迭代器失效问题
文章目录 模拟实现vector基本成员变量vector的构造与析构vector迭代器vector容量vector元素访问vector修改操作 vector迭代器失效问题什么是迭代器失效1.插入元素导致迭代器失效2.删除元素导致迭代器失效3.重新分配空间导致迭代器失效 如何解决迭代器失效问题 模拟实现 vector…...

USB 3.1 标准 A 型连接器及其引脚分配
USB 3.1 标准 A 型连接器 USB 3.1 标准 A 型连接器被定义为主机连接器。它具有与 USB 2.0 标准 A 型连接器相同的配合接口,但增加了另外两对差分信号和一个接地引脚。 USB 3.1 标准 A 型插座可以接受 USB 3.1 标准 A 型插头或 USB 2.0 标准 A 型插头。类似地&…...

机器学习文献|基于循环细胞因子特征,通过机器学习算法预测NSCLC免疫治疗结局
今天我们一起学习一篇最近发表在Journal for immunotherapy of cancer (IF 10.9)上的文章,Machine learning for prediction of immunotherapeutic outcome in non-small-cell lung cancer based on circulating cytokine signatures[基于循环…...

Qt 实现自定义截图工具
目录 Qt 实现自定义截图工具实现效果图PrintScreen 类介绍PrintScreen 类的主要特性 逐步实现第一步:类定义第二步:初始化截图窗口第三步:处理鼠标事件第四步:计算截图区域第五步:捕获和保存图像 完整代码PrintScreen.…...

第15-05章:获取运行时类的完整结构
我的后端学习大纲 我的Java学习大纲 6.1.第一组方法API: 1.API列表:java.lang.Class 类: 2.代码测试: public class ReflectionUtils{ puvblic static void main(String[] args){}// 第一组Testpublic void api_01{//上面截图的代码......…...

【Kubernetes】K8s 的鉴权管理(二):基于属性 / 节点 / Webhook 的访问控制
K8s 的鉴权管理(二):基于属性 / 节点 / Webhook 的访问控制 1.基于属性的访问控制(ABAC 鉴权)2.基于节点的访问控制(node 鉴权)2.1 读取操作2.2 写入操作 3.基于 Webhook 的访问控制3.1 基于 We…...

Java面试、技巧、问题、回复,资源面面观
入门 先了解一下面试流程 复习 Java 基础知识: 温习 Java 编程的核心概念,包括数据类型、变量、循环、数组和面向对象的编程原则。数据结构和算法: 加强您对 Java 编程中使用的基本数据结构和算法的理解。练习编码: 在各种平台上解…...

深入理解Elasticsearch的`_source`字段与索引优化
在Elasticsearch (ES) 中,_source字段是一个关键组件,它不仅决定了数据的存储方式,还影响到查询时返回的内容。在某些场景下,我们可以通过配置_source来优化存储和性能,尤其是当我们希望减少存储空间或避免返回某些字段…...
Pikachu靶场
先来点鸡汤,少就是多,慢就是快。 环境搭建 攻击机kali 192.168.146.140 靶机win7 192.168.146.161 下载zip,pikachu - GitCode 把下载好的pikachu-master,拖进win7,用phpstudy打开网站根目录,.....再用…...

TS axios封装
方式一 service/request/request.ts import axios from axios import { ElLoading } from element-plus import type { AxiosRequestConfig, AxiosInstance, AxiosResponse } from axios import type { ILoadingInstance } from element-plus/lib/el-loading/src/loading.typ…...

学会使用西门子博途Startdrive中的测量功能
工程师在驱动调试过程中,往往需要对驱动系统的性能进行分析及优化,比如说借助于调试软件中的驱动器测量功能,可以得到驱动系统的阶跃响应、波特图等,以此为依据工程师可以调整速度控制器、电流控制器的相关参数,使驱动…...
Spring Security认证与授权
1 Spring Security介绍 Spring Security是一个能够为基于Spring的企业应用系统提供声明式的安全访问控制解决方案的安全框架。由于它是Spring生态系统中的一员,因此它伴随着整个Spring生态系统不断修正、升级,在spring boot项目中加入springsecurity更是…...
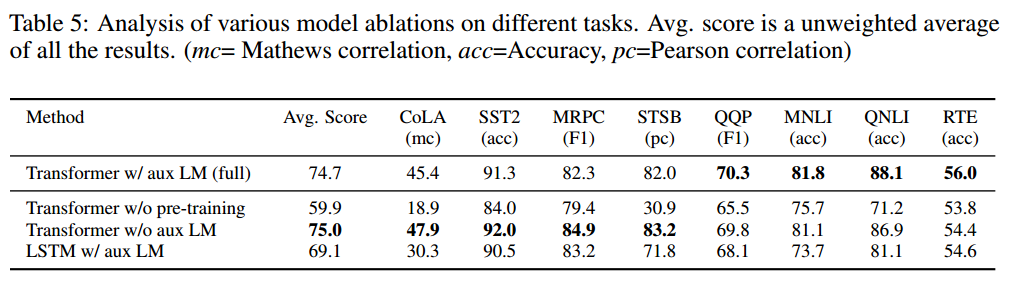
速通GPT:Improving Language Understanding by Generative Pre-Training全文解读
文章目录 速通GPT系列几个重要概念1、微调的具体做法2、任务感知输入变换3、判别式训练模型 Abstract概括分析和观点1. 自然语言理解中的数据问题2. 生成预训练和监督微调的结合3. 任务感知输入变换4. 模型的强大性能 Introduction概括分析和观点1. 自然语言理解的挑战在于对标…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...
