LeetCode: 2552. 统计上升四元组 动态规划 时间复杂度O(n*n)
2552. 统计上升四元组
today 2552. 统计上升四元组
题目描述
给你一个长度为n下标从 0 开始的整数数组 nums ,它包含1到n的所有数字,请你返回上升四元组的数目。
如果一个四元组 (i, j, k, l) 满足以下条件,我们称它是上升的:
0 <= i < j < k < l < n且nums[i] < nums[k] < nums[j] < nums[l]。
示例 1:
输入:nums = [1,3,2,4,5]
输出:2
解释:
- 当 i = 0 ,j = 1 ,k = 2 且 l = 3 时,有 nums[i] < nums[k] < nums[j] < nums[l] 。
- 当 i = 0 ,j = 1 ,k = 2 且 l = 4 时,有 nums[i] < nums[k] < nums[j] < nums[l] 。
没有其他的四元组,所以我们返回 2 。
示例 2:
输入:nums = [1,2,3,4]
输出:0
解释:没有四元组,所以我们返回 0 。
提示:
4 <= nums.length <= 40001 <= nums[i] <= nums.lengthnums 中所有数字 互不相同 ,nums 是一个排列。
解题思路
我们可以枚举四元组中的 j 和 k,那么问题转化为,对于当前的 j 和 k:
统计有多少个 l 满足 l>k 且 nums[l]>nums[j],记为cnt1;
统计有多少个 i 满足 i<j 且 nums[i]<nums[k],记为cnt2;
所以,对于每一组 j 和 k,满足条件的组合数目为cnt1*cnt2,将所有j 和 k组合数目相加,就是答案。
那么我们可以用动态规划解决这个问题。
使用二维数组 f 来记录 j 和 k 组合的情况,f[j][k] 表示 有多少个l满足满足 l>k 且 nums[l]>nums[j]。
初始化 f[j][n-1] 为 0,表示对于末尾元素为k的情况下,没有满足条件的l。注意1<=j<n-2。
从后往前填充行f[j],如果nums[k]>nums[j],则f[j][k-1]=f[j][k]+1。
此时,对于每个j 和 k,我们都可以计算出有多少个 l 满足 l>k 且 nums[l]>nums[j],即cnt1=f[j][k]。
对于每个j 和 k,我们已经通过二维数组 f,记录了cnt1的取值,接下来,我们只需要记录cnt2的取值即可。
对于每个j 和 k,我们可以确定k,,之后从前往后遍历数组。
初始化cnt2=0,如果
nums[j]<nums[k],则cnt2+=1,表示当前有多少个i满足nums[i]<nums[k]。nums[j]>nums[k],则当前j和k满足条件,我们将cnt2*cnt1即cnt2*f[j][k]加入答案。
最后,返回答案即可。
复杂度分析:
- 时间复杂度: O ( n 2 ) O(n^2) O(n2),其中 n n n 是数组的长度。
- 空间复杂度: O ( n 2 ) O(n^2) O(n2),其中 n n n 是数组的长度。
代码实现
Python实现:
class Solution(object):def countQuadruplets(self, nums):n=len(nums)f=[[0]*n for i in range(n)]ans=0for j in range(1,n-2):cnt=0for k in range(n-1,j,-1):f[j][k]=cntif nums[k]>nums[j]:cnt+=1for k in range(2,n-1):cnt=0for j in range(0,k):if(nums[j]>nums[k]):ans+=cnt*f[j][k]else:cnt+=1return ans
C++实现:
class Solution {
public:long long countQuadruplets(vector<int>& nums) {int n=nums.size();vector<vector<int>> f(n,vector<int>(n,0));long long res=0;for(int j=1;j<n-2;j++){int cnt=0;for(int k=n-1;k>j;k--){f[j][k]=cnt;if(nums[k]>nums[j]){cnt++;}}}for(int k=2;k<n-1;k++){int cnt=0;for(int j=0;j<k;j++){if(nums[j]<nums[k]){cnt++;continue;}else{res+=cnt*f[j][k];}}}return res;}
};
Go实现:
func countQuadruplets(nums []int) int64 {n := len(nums)f := make([][]int, n)for i := range f {f[i] = make([]int, n)}for j := 1; j < n-2; j++ {cnt := 0for k := n-1; k >j; k-- {f[j][k] = cntif nums[j] < nums[k] {cnt++} }}ans := 0for k := 2; k < n-1; k++ {cnt := 0for j := 0; j <k; j++ {if nums[j] < nums[k] {cnt++continue}else{ans+=cnt*f[j][k]}}}return int64(ans)
}
相关文章:
)
LeetCode: 2552. 统计上升四元组 动态规划 时间复杂度O(n*n)
2552. 统计上升四元组 today 2552. 统计上升四元组 题目描述 给你一个长度为n下标从 0 开始的整数数组 nums ,它包含1到n的所有数字,请你返回上升四元组的数目。 如果一个四元组 (i, j, k, l) 满足以下条件,我们称它是上升的:…...

Unity 编辑器设置中文
在 Unity 编辑器中,你可以按照以下步骤将语言设置为中文: 步骤: 1. 打开 Unity 编辑器。 2. 在顶部菜单栏,依次点击 Edit > Preferences(在 macOS 上是 Unity > Preferences)。 3. 在弹出的 Preferen…...

springboot-创建连接池
操作数据库 代码开发步骤: pom.xml文件配置依赖properties文件配置连接数据库信息(连接池用的是HikariDataSource)数据库连接池开发 configurationproperties和value注解从properties文件中取值bean方法开发 service层代码操作数据库 步骤&am…...

matlab绘制不同区域不同色彩的图,并显示数据(代码)
绘图结果如下: 代码如下: A为绘图的数据,每个数据对应着上图中的一个区域,数据大小决定区域的颜色 % 假设有一系列的数据点 Arand(5,6); %A为绘图的数据,数据大小决定颜色 wei_shu%.3f; %代表数据保留三位小…...

Docker Desktop 的安装与汉化指南
前言 Docker Desktop 是一款非常流行的开发工具,它使得开发者能够在自己的计算机上轻松地构建、运行和调试 Docker 容器。然而,默认情况下,Docker Desktop 的界面是英文的,对于中文用户来说,有时候会觉得不够友好。幸…...

前端form表单+ifarme方式实现大文件下载
// main.jsimport Vue from vue; import App from ./App.vue; import { downloadTokenFile } from /path/to/your/function; // 替换为您的函数路径// 将 downloadTokenFile 添加到 Vue 原型上 Vue.prototype.$downloadTokenFile downloadTokenFile;new Vue({el: #app,render:…...

Leetcode面试经典150题-141.环形链表
题目比较简单,重点是理解思想 解法都在代码里,不懂就留言或者私信 /*** Definition for singly-linked list.* class ListNode {* int val;* ListNode next;* ListNode(int x) {* val x;* next null;* }* }*/ public…...

sh文件执行提示语法错误: 未预期的文件结尾
在执行sh文件时总是提示:语法错误: 未预期的文件结尾,尝试删除最后的空格也不对 最后发现在notepad中转换的问题 需要把windows换成unix就行了...

基于SpringBoot的甜品店管理系统
作者:计算机学姐 开发技术:SpringBoot、SSM、Vue、MySQL、JSP、ElementUI等,“文末源码”。 专栏推荐:前后端分离项目源码、SpringBoot项目源码、SSM项目源码 系统展示 【2025最新】基于JavaSpringBootVueMySQL的蛋糕甜品店管理系…...

动态规划-不同的子序列
题目描述 给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 109 7 取模。 示例: 输入:s "babgbag", t "bag" 输出:5 解释: 如下所示, 有 5 种可以从…...
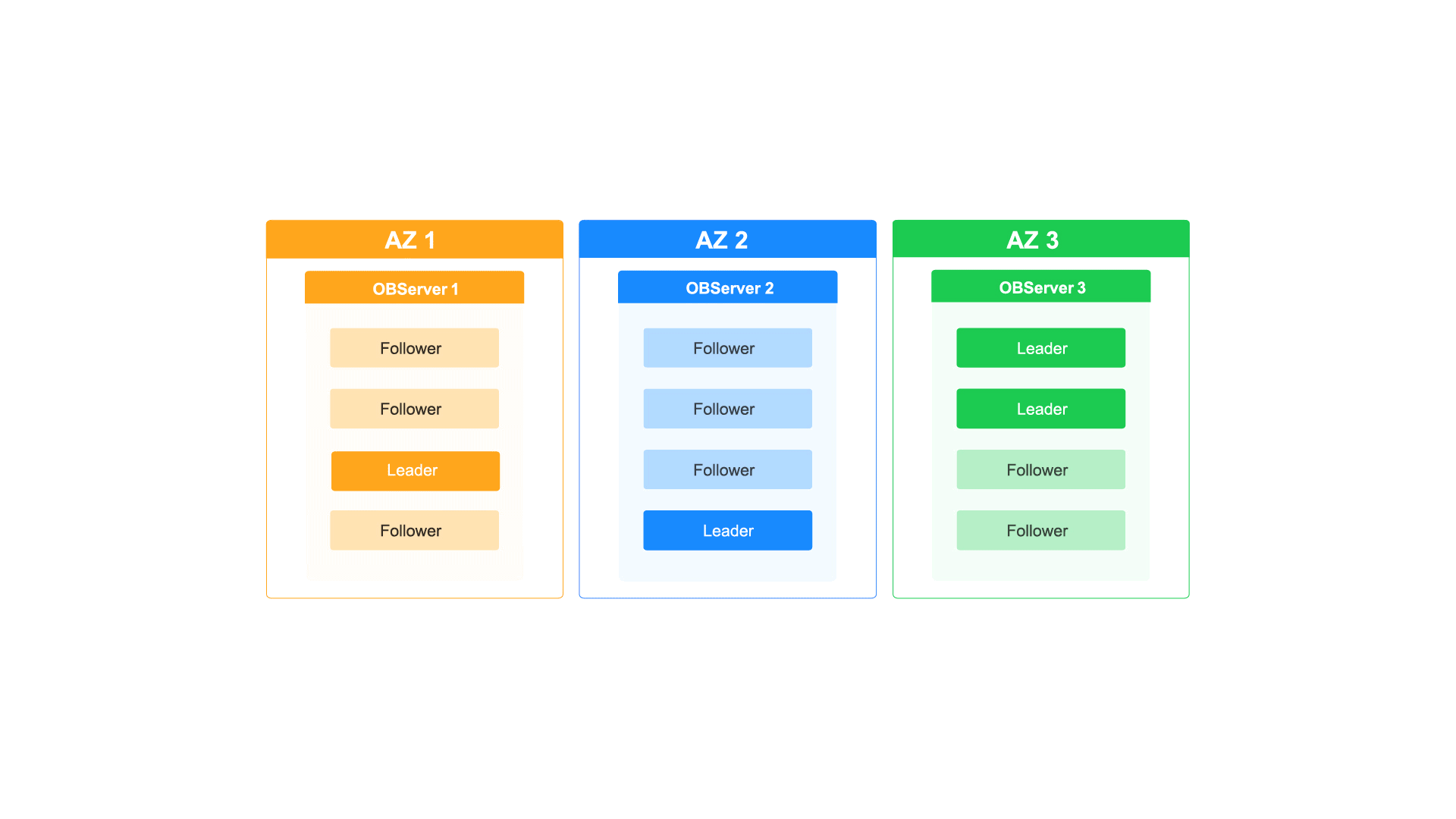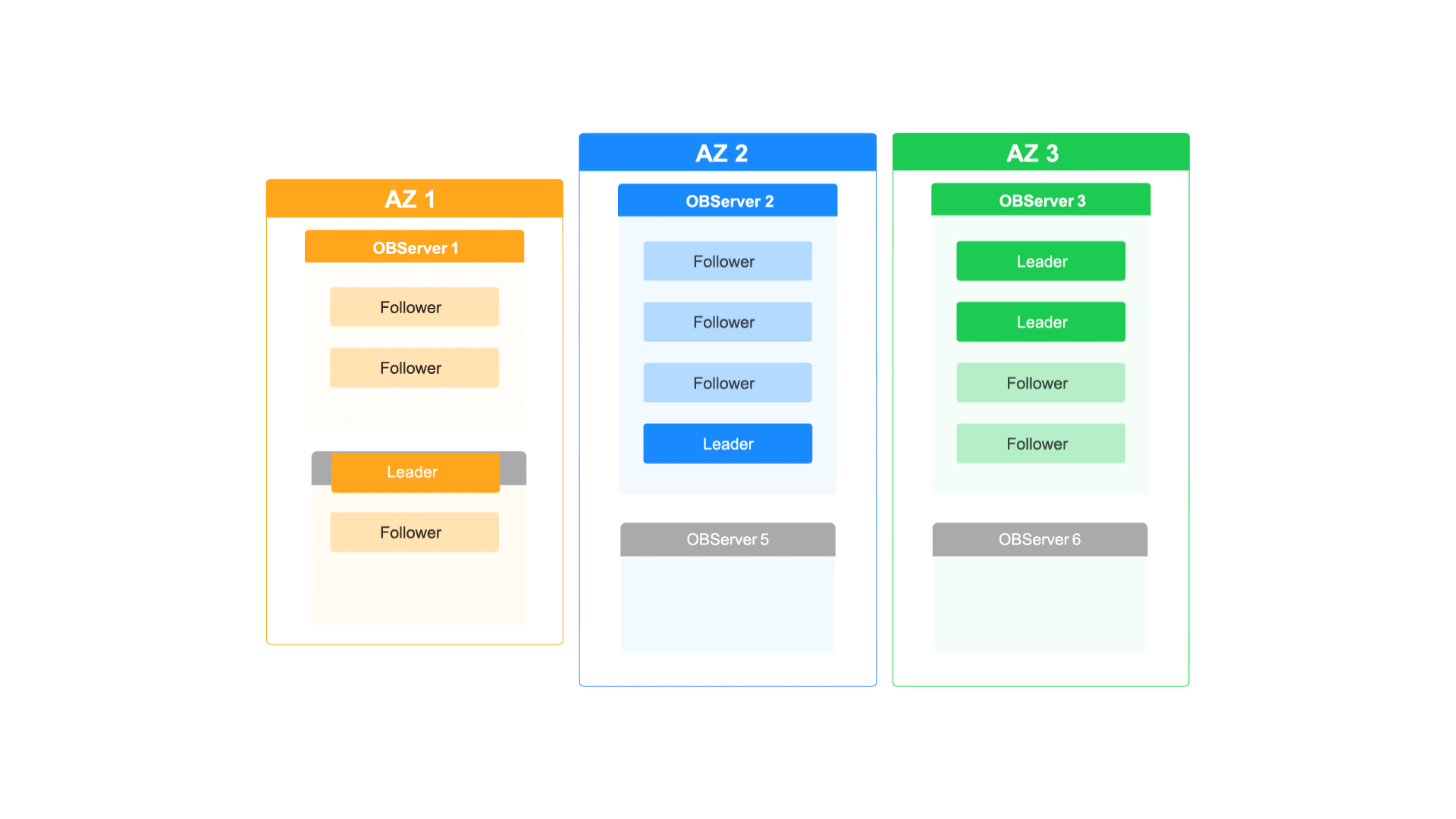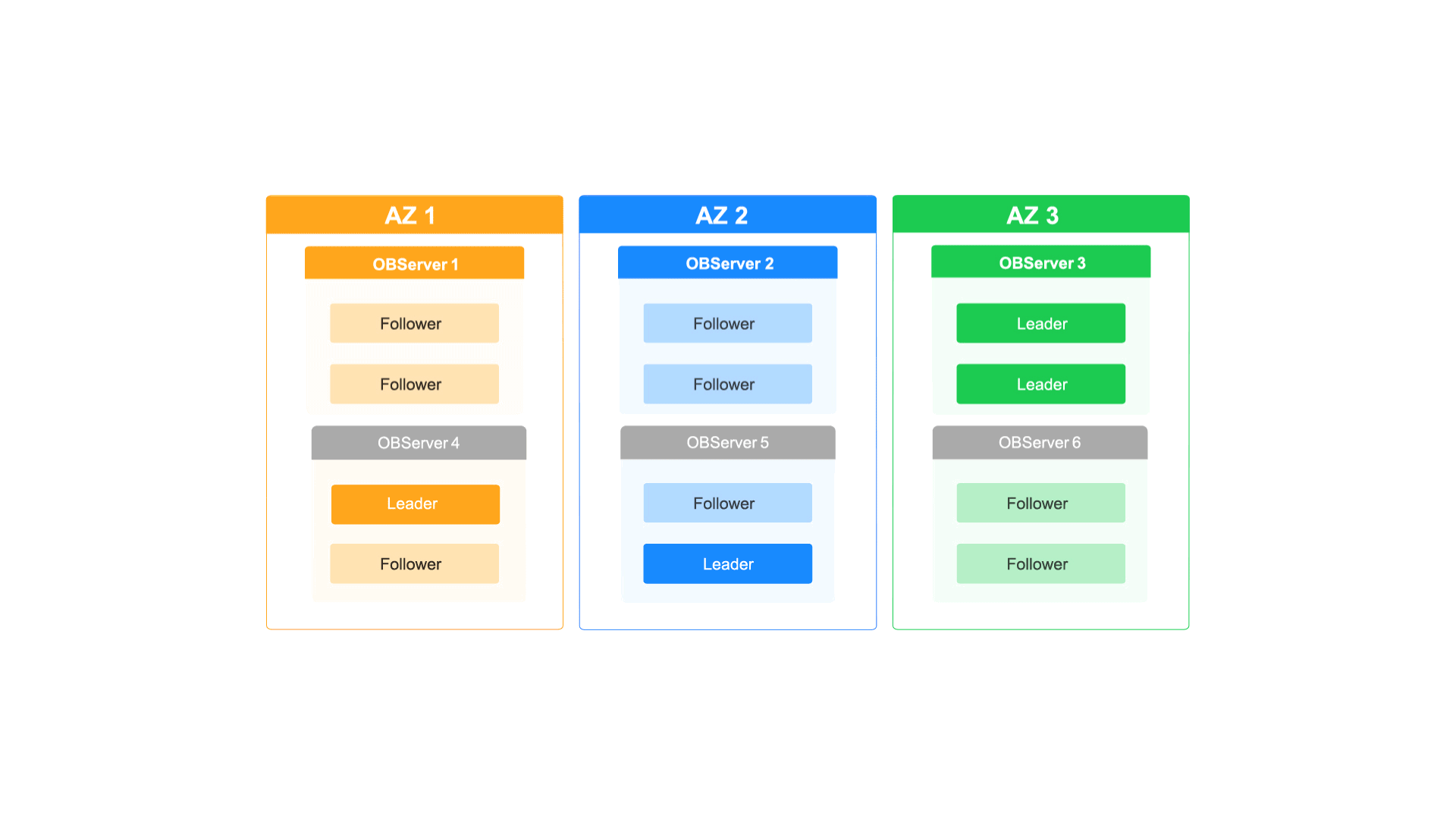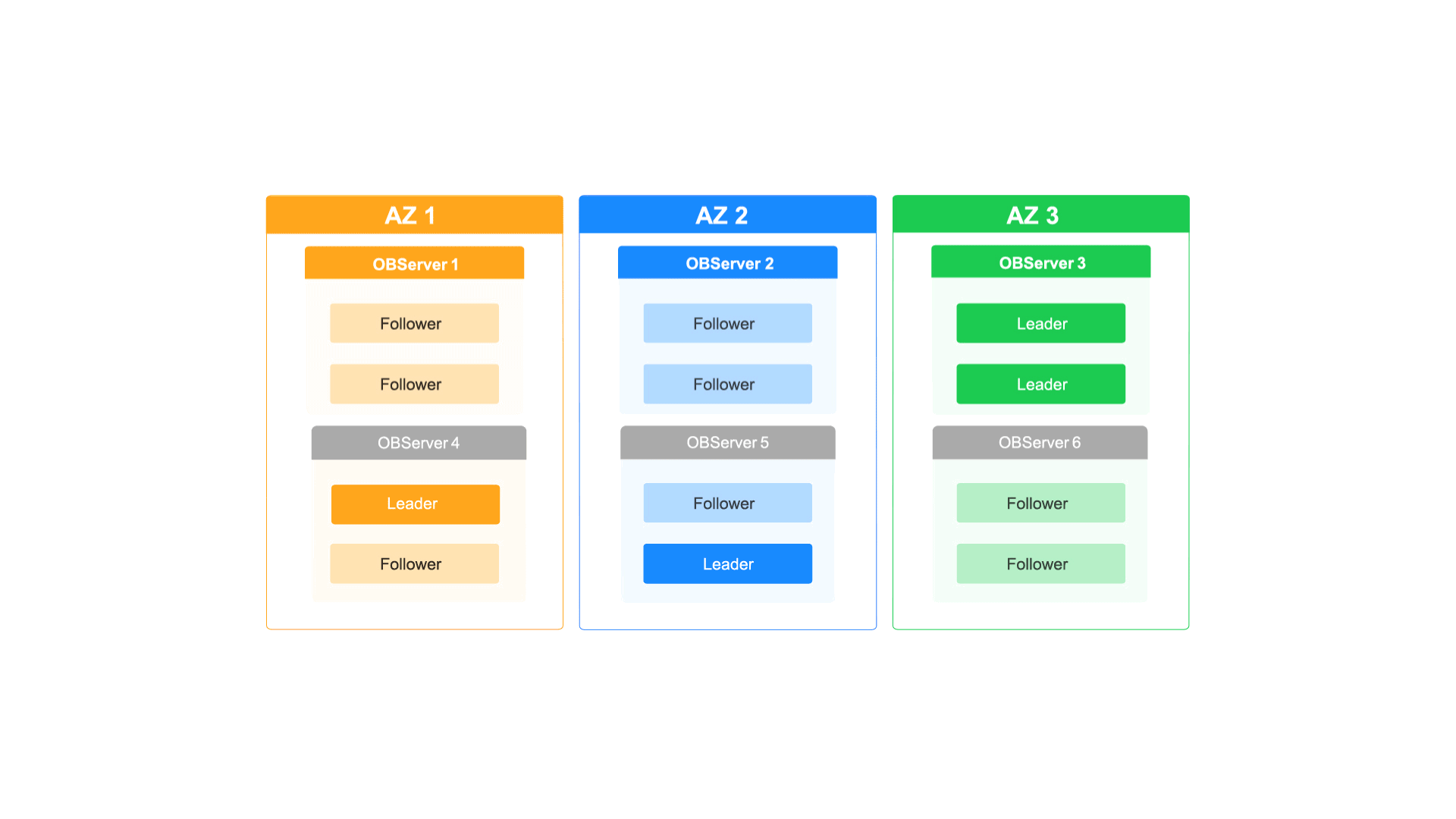
如何通过OceanBase的多级弹性扩缩容能力应对业务洪峰
每周四晚上的10点,都有近百万的年轻用户进入泡泡玛特的抽盒机小程序,共同参与到抢抽盲盒新品的活动中。瞬间的并发流量激增对抽盒机小程序的系统构成了巨大的挑战,同时也对其数据库的扩容能力也提出了更高的要求。 但泡泡玛特的工程师们一点…...

D - 1D Country(AtCoder Beginner Contest 371)
题目链接: D - 1D Country (atcoder.jp) 题目描述: 数据范围: 输入输出: 题目分析: 典型的l, r 区间问题,即是前缀和问题,但是注意到数据范围, 数据范围1e-9 到 1e9 数据范围,要是从最小到最大直接for循环去模拟的话,时间复杂度…...
怎么很多张图片拼接成一张?试试这几种图片拼接方法!
怎么很多张图片拼接成一张?在繁忙的现代生活中,我们不断地捕捉和累积着各式各样的图像,它们如同记忆的珍珠,串联起生活的每一个瞬间,然而,随图片数量的激增,管理它们成为了一项挑战,…...

Python实现优化的分水岭算法
目录 优化分水岭算法的博客1. 分水岭算法优化概述2. 优化分水岭算法的步骤3. Python实现优化后的分水岭算法4. 实例:优化分水岭算法在图像分割中的应用5. 总结 优化分水岭算法的博客 分水岭算法是一种强大的图像分割方法,特别适用于分离不同的对象和区域…...

智慧交通基于yolov8的行人车辆检测计数系统python源码+onnx模型+精美GUI界面
【算法介绍】 智慧交通中,基于YOLOv8的行人车辆检测计数系统是一项高效、准确的技术解决方案。该系统利用YOLOv8这一先进的目标检测算法,结合深度学习技术,能够实时检测并准确计数道路上的行人和车辆。YOLOv8在保证检测速度的同时࿰…...

Linux开发工具的使用
文章目录 vim的使用基本模式介绍光标当前行操作(命令行模式)光标快速定位(命令行模式):插入模式的三种方式(命令行模式):vim基本操作(命令行模式)底行模式的操…...
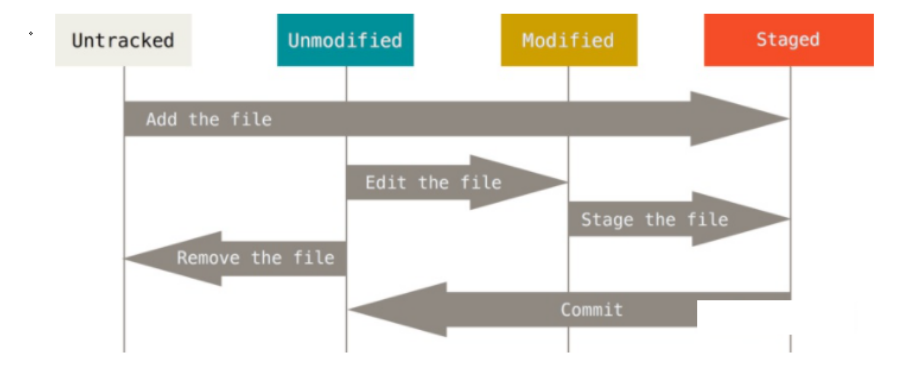
【devops】devops-git之介绍以及日常使用
本站以分享各种运维经验和运维所需要的技能为主 《python零基础入门》:python零基础入门学习 《python运维脚本》: python运维脚本实践 《shell》:shell学习 《terraform》持续更新中:terraform_Aws学习零基础入门到最佳实战 《k8…...

012复杂度07leetcode
视频地址:012复杂度07leetcode_哔哩哔哩_bilibili 网站叫做leetcode。那Linux我相信很多同学都听过这个网站,那这个网站干嘛用呢?这个网站是用于练习算法的一个好网站,那我们这个课程在讲解知识点过程中也会不断的去用到这个网站,…...

4.网络编程
1、目的 传播交流信息TCP:打电话UDP:发短信 2、通信协议: httpTCP/IP簇:三次握手(aba),四次挥手(abba)https 3、IP与端口 1.IP地址类:InetAddress、InetSocketAddress InetAdd…...
OpenCV GUI常用函数详解
在OpenCV的High_level GUI模组中有很多GUI函数,下面介绍几个常用的函数。 图像显示窗口相关函数 生成图像显示窗口函数nameWindow() nameWindow()函数的原型如下: 函数用以创建一个给定名的图像显示窗口(后面简单叫做图像窗口)…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...
