医学数据分析实训 项目二 数据预处理预备知识(数据标准化处理,数据离差标准化处理,数据二值化处理,独热编码处理,数据PCA降维处理)
文章目录
- 数据预处理预备知识
- 任务一 数据标准化处理
- 1. 数据准备
- 2. 数据标准化
- 任务二 数据离差标准化处理
- 任务三 数据二值化处理
- 任务五 独热编码处理
- 对数据进行“离散化处理”(装箱)
- 将已经装箱的数据进行OneHotEncoder独热编码
- 任务六 数据PCA降维处理
- 1. 导入iris(鸢尾花)数据集
- 2. 指定特征数的PCA降维
- 3. 保留方差百分比的PCA降维
- 项目拓展
- 数据预处理实战——wine酒数据集拆分、标准化和降维处理
数据预处理预备知识
任务一 数据标准化处理
使用StandardScaler进行数据预处理
- StandardScaler类是一个用来将数据进行归一化和标准化的类。
- 将数据按其属性(按列进行)减去平均值和缩放到单位方差来标准化特征。得到的结果是,对于每个属性/每列来说所有数据都聚集在0附近,标准差为1,使得新的X数据集方差为1,均值为0
- 在进行标准化的过程中就将训练集的均值和方差当做是总体的均值和方差,因此对测试集使用训练集的均值和方差进行预处理。
- 适用范围:如果数据的分布本身就服从正态分布,就可以用这个方法。
# StandardScaler类的使用
from sklearn.preprocessing import StandardScaler
import numpy as npX = np.array([[1., -1., 2.],[2., 0., 0.],[0., 1., -1.]])
# 计算平均值
X_mean = X.mean(axis=0)
# 计算方差
X_std = X.std(axis=0)
# 标准化X
X1 = (X - X_mean) / X_std # 自己计算# 调用sklearn包的方法
X_scale = StandardScaler().fit_transform(X)
# 最终X1与X_scale等价
print('均值方差标准化后的数据:\n', X1)
print('StandardScaler标准差标准化后的数据:\n', X_scale)

1. 数据准备
import matplotlib.pyplot as plt
# 导入数据集生成工具
from sklearn.datasets import make_blobsplt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号# 生成一个样本量为50,分类数为1,标准差为1的聚类数据集
X, y = make_blobs(n_samples=50, centers=1, cluster_std=1, random_state=8)
# 用散点图绘制数据点
plt.scatter(X[:, 0], X[:, 1], c='blue')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.title('原始数据')
plt.show()

2. 数据标准化
# 导入StandardScaler
from sklearn.preprocessing import StandardScaler# 使用StandardScaler进行数据处理,用于将数据转换为均值为 0,标准差为 1 的标准正态分布。
scaler = StandardScaler().fit(X)
X_1 = scaler.transform(X)
# 也可以用fit_transform()实现
# X_1 = StandardScaler().fit_transform(X)# 用散点图绘制经过预处理的数据点
plt.scatter(X_1[:, 0], X_1[:, 1], c='blue')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.title('均值方差标准化数据')
plt.show()

任务二 数据离差标准化处理
- 将每个元素(特征,feature)转换成给定范围的值。
- MinMaxScaler有一个重要参数"feature_range",控制数据压缩到的范围,默认是[0,1]。
- 适用范围:适用于数据在一个范围内分布的情况,在不涉及距离度量、协方差计算、数据不符合正态分布的时候,可以使用MinMaxScaler。
# 导入MinMaxScaler
from sklearn.preprocessing import MinMaxScaler# 使用MinMaxScaler进行数据预处理
X_2 = MinMaxScaler().fit_transform(X)
# 绘制散点图
plt.scatter(X_2[:, 0], X_2[:, 1], c='blue')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.title('离差标准化数据')
plt.show()

任务三 数据二值化处理
- 特征的二值化主要是为了将数据特征转化为boolean变量
- Binarizer也可以设置一个阈值,结果数据值大于阈值的为1,小于阈值的为0
import numpy as np
# 导入Binarizer
from sklearn.preprocessing import Binarizerdata = np.array([[3, -1.5, 2, -5.4],[0, 4, -0.3, 2.1],[1, 3.3, -1.9, -4.3]])
# 特征二值化
data_binarized = Binarizer(threshold=1.4).transform(data)
print("二值化处理后的数据: \n", data_binarized)

## 任务四 数据归一化处理
- normalizer 数据归一化使每个特征向量的值都缩放到相同的数值范围。归一化的形式有l1,l2范数等
- sklearn.preprocessing.Normalizer(norm='l2', copy=True) - norm:可以为l1、l2或max,默认为l2- 若为l1时,样本各个特征值除以各个特征值的绝对值之和- 若为l2时,样本各个特征值除以各个特征值的平方之和- 若为max时,样本各个特征值除以样本中特征值最大的值
# 导入Normalizer
from sklearn.preprocessing import Normalizer# 使用Normalizer进行数据预处理,默认为l2范数
# 将所有样本的特征向量转化为欧几里得距离为1;通常在只想保留数据特征向量的方向,而忽略其数值的时候使用
X_3 = Normalizer().fit_transform(X)
# 绘制散点图
plt.figure(figsize=(6, 6))
plt.scatter(X_3[:, 0], X_3[:, 1], c='blue')
plt.xlim(0, 1.1)
plt.ylim(0, 1.1)
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.title('L2范数的归一化化处理')
plt.show()

# 修改norm参数为范数l1
X_4 = Normalizer(norm='l1').fit_transform(X)
# 绘制散点图
plt.figure(figsize=(6, 6))
plt.scatter(X_4[:, 0], X_4[:, 1], c='blue')
plt.xlim(0, 1.1)
plt.ylim(0, 1.1)
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.title('L1范数的归一化化处理')
plt.show()

任务五 独热编码处理
- 独热编码(One-Hot Encoding)把特征向量的每个特征与特征的非重复总数相对应,通过one-of-k的形式对每个值进行编码,如果非重复计数的值是k,那么就把这个特征转换为只有一个值是1其他值都是0的k维向量。
- OneHotEncoder 参数:
- categories: 表示特征的取值,该参数取值为list或者默认的’auto’
import numpy as np
# 导入OneHotEncoder
from sklearn.preprocessing import OneHotEncoderdata_type = np.array([[0, 1],[1, 3],[2, 0],[1, 2]])
print(data_type)
encoder = OneHotEncoder(categories='auto').fit(data_type)
data_encoded = encoder.transform(data_type).toarray()
print("编码后的数据: \n", data_encoded)

对数据进行“离散化处理”(装箱)
- numpy.digitize(x, bins, right = False)
- 该函数返回输入数组x中每个值所属的数组bins的区间索引。
- 参数:
- x : numpy数组
- bins : 一维单调数组,必须是升序或者降序
- right:间隔是否包含最右
- 返回值:x在bins中的位置。
import numpy as np# 定义一个随机数的数组
np.random.seed(38)
arr = np.random.uniform(-5, 5, size=20)
# 设置箱体数为5
bins = np.linspace(-5, 5, 6)
# 将数据进行装箱操作
target_bin = np.digitize(arr, bins=bins)
# 打印装箱数据范围
print('装箱数据范围:\n{}'.format(bins))
print('\n数据点的特征值:\n{}'.format(arr))
print('\n数据点所在的箱子:\n{}'.format(target_bin))

将已经装箱的数据进行OneHotEncoder独热编码
from sklearn.preprocessing import OneHotEncoder# 假设 target_bin 是你的目标变量
target_bin = target_bin.reshape(-1, 1)# 初始化 OneHotEncoder,注意这里不需要设置 sparse 参数, 因为sparse参数已经被移除
# onehot = OneHotEncoder(sparse=False, categories='auto')
onehot = OneHotEncoder(categories='auto')# 拟合并转换数据
onehot.fit(target_bin)
arr_in_bin = onehot.transform(target_bin)# 打印结果
print('装箱编码后的数据形态:{}'.format(arr_in_bin.shape))
print('\n装箱编码后的数据值:\n{}'.format(arr_in_bin))
任务六 数据PCA降维处理
- PCA通过计算协方差矩阵的特征值和相应的特征向量,在高维数据中找到最大方差的方向,并将数据映射到一个维度不大于原始数据的新的子空间中。
1. 导入iris(鸢尾花)数据集
# 导入iris(鸢尾花)数据集
from sklearn.datasets import load_iris# 加载iris数据集
iris = load_iris()
X = iris.data
print('iris数据集的维度为:', X.shape)print('iris数据集的前5行数据为:\n', X[:5])

2. 指定特征数的PCA降维
# 导入PCA
from sklearn.decomposition import PCA# 指定保留的特征数为3
pca_num = PCA(n_components=3)
# 训练PCA模型
pca_num.fit(X)
# 对样本数据进行PCA降维
X_pca1 = pca_num.transform(X)
# 查看降维结果
print('iris数据集进行指定特征数的降维后的维度为:', X_pca1.shape)
# 查看降维后的前5行数据
print('指定特征数的降维后iris数据集的前5行数据为:\n', X_pca1[:5])

# 查看原始特征与PCA主成分之间的关系
import numpy as npprint('指定特征数的降维后的最大方差的成分:')
for i in range(pca_num.components_.shape[0]):arr = np.around(pca_num.components_[i], 2)print('component{0}: {1}'.format((i + 1), [x for x in arr]))

# 查看降维后的各主成分的方差值和方差占比
var = np.around(pca_num.explained_variance_, 2)
print('指定特征数的降维后的各主成分的方差为:', [x for x in var])
var_ratio = np.round(pca_num.explained_variance_ratio_, 2)
print('指定特征数的降维后的各主成分的方差百分比为:', [x for x in var_ratio])

3. 保留方差百分比的PCA降维
# 指定保留的方差百分比为0.95
pca_per = PCA(n_components=0.95)
# 训练PCA模型
pca_per.fit(X)
# 对样本数据进行PCA降维
X_pca2 = pca_per.transform(X)
# 查看降维结果
print('iris数据集进行指定方差百分比的降维后的维度为:', X_pca2.shape)
# 查看降维后的前5行数据
print('指定方差百分比的降维后iris数据集的前5行数据为:\n', X_pca2[:5])

# 查看原始特征与PCA主成分之间的关系
print('指定方差百分比降维后的最大方差的成分:')
for i in range(pca_per.components_.shape[0]):arr = np.round(pca_per.components_[i], 2)print('component{0}: {1}'.format((i + 1), [x for x in arr]))

# 查看降维后的各主成分的方差值和方差占比
var = np.around(pca_per.explained_variance_, 2)
print('指定方差百分比的降维后的各主成分的方差为:', [x for x in var])
var_ratio = np.round(pca_per.explained_variance_ratio_, 2)
print('指定方差百分比的降维后的各主成分的方差百分比为:', [x for x in var_ratio])

项目拓展
数据预处理实战——wine酒数据集拆分、标准化和降维处理
# 1. 导入wine酒数据集
# 导入wine酒模块
from sklearn.datasets import load_wine
import numpy as np# 加载wine数据集
wine = load_wine()
# “input”是特征数据
X = wine.data
# “target”是目标变量数据(酒的类别标签)
y = wine.target
# 查看特征数据的维度
print('wine数据集的维度为:', X.shape)
# 查看酒的类别
print('wine数据集的类别标签为:', np.unique(y))

# 2. 将wine数据集划分为训练集和测试集
# 导入数据集拆分工具
from sklearn.model_selection import train_test_split# 将数据集拆分为训练数据集和测试数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=8)# 输出训练数据集中特征向量的维度
print('训练集数据维度:', X_train.shape)
# 输出训练数据集中目标标签的维度
print('训练集标签维度:', y_train.shape)
# 输出测试数据集中特征向量的维度
print('测试集数据维度:', X_test.shape)
# 输出测试数据集中特征向量的维度
print('测试集标签维度:', y_test.shape)

# 3. 对数据集进行标准化处理
# 导入StandardScaler
from sklearn.preprocessing import StandardScaler
# 对训练集进行拟合生成规则
scaler = StandardScaler().fit(X_train)
# 对训练集数据进行转换
X_train_scaled = scaler.transform(X_train)
# 对测试集数据进行转换
X_test_scaled = scaler.transform(X_test)print('标准化前训练集数据的最小值和最大值:{0}, {1}'.format(X_train.min(), X_train.max()))
print('标准化后训练集数据的最小值和最大值:{0:.2f}, {1:.2f}'.format(X_train_scaled.min(), X_train_scaled.max()))
print('标准化前测试集数据的最小值和最大值:{0}, {1}'.format(X_test.min(), X_test.max()))
print('标准化后测试集数据的最小值和最大值:{0:.2f}, {1:.2f}'.format(X_test_scaled.min(), X_test_scaled.max()))

# 4. 对数据进行降维处理
# 导入PCA
from sklearn.decomposition import PCA
# 设置主成分数量为2
pca = PCA(n_components=2)
# 对标准化后的训练集进行拟合生成规则
pca.fit(X_train_scaled)
# 对标准化后的训练集数据进行PCA降维
X_train_pca = pca.transform(X_train_scaled)
# 对标准化后的测试集数据进行PCA降维
X_test_pca = pca.transform(X_test_scaled)print('降维后训练集的维度为:', X_train_pca.shape)
print('降维后测试集的维度为:', X_test_pca.shape)

# 5. wine数据集可视化
import numpy as np
import matplotlib.pyplot as pltplt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号# 绘制wine数据集图形
plt.figure(figsize=(8, 6))
for i, color, name in zip(np.unique(y), ['r','g','b'], wine.target_names):# 绘制降维后的训练集样本图形plt.scatter(X_train_pca[y_train==i,0], X_train_pca[y_train==i,1],c=color, marker='o', label='类别'+name+'训练集')# 绘制降维后的测试集样本图形plt.scatter(X_test_pca[y_test==i,0], X_test_pca[y_test==i,1],c=color, marker='*', label='类别'+name+'测试集')plt.xlabel("成分1")
plt.ylabel("成分2")
plt.legend(loc='best')
plt.show()

相关文章:

医学数据分析实训 项目二 数据预处理预备知识(数据标准化处理,数据离差标准化处理,数据二值化处理,独热编码处理,数据PCA降维处理)
文章目录 数据预处理预备知识任务一 数据标准化处理1. 数据准备2. 数据标准化 任务二 数据离差标准化处理任务三 数据二值化处理任务五 独热编码处理对数据进行“离散化处理”(装箱)将已经装箱的数据进行OneHotEncoder独热编码 任务六 数据PCA降维处理1.…...

MySQL查询执行(四):查一行也很慢
假设存在表t,这个表有两个字段id和c,并且我在里面插入了10万行记录。 -- 创建表t CREATE TABLE t (id int(11) NOT NULL,c int(11) DEFAULT NULL,PRIMARY KEY (id) ) ENGINEInnoDB;-- 通过存储过程向t写入10w行数据 delimiter ;; create procedure idat…...

【Obsidian】当笔记接入AI,Copilot插件推荐
当笔记接入AI,Copilot插件推荐 自己的知识库笔记如果增加AI功能会怎样?AI的回答完全基于你自己的知识库余料,是不是很有趣。在插件库中有Copilot插件这款插件,可以实现这个梦想。 一、什么是Copilot? 我们知道githu…...

Spring Cloud集成Gateaway
Spring Cloud Gateway 是一个基于 Spring 生态的网关框架,用于构建微服务架构中的API网关。它可以对请求进行路由、过滤、限流等操作,是Spring Cloud微服务体系中常用的组件之一。下面介绍 Spring Cloud Gateway 的核心概念、应用场景以及简单的示例。 …...

如何准备技术面试?
大家好,我是老三,好久没更新了,翻出之前的一篇旧稿,是一篇总纲性质的文章——如何准备一场技术面试。这篇文章原本的开头是写给金三银四的,转眼就“金九银十”了,每一年都是最差的一年,又是未来…...
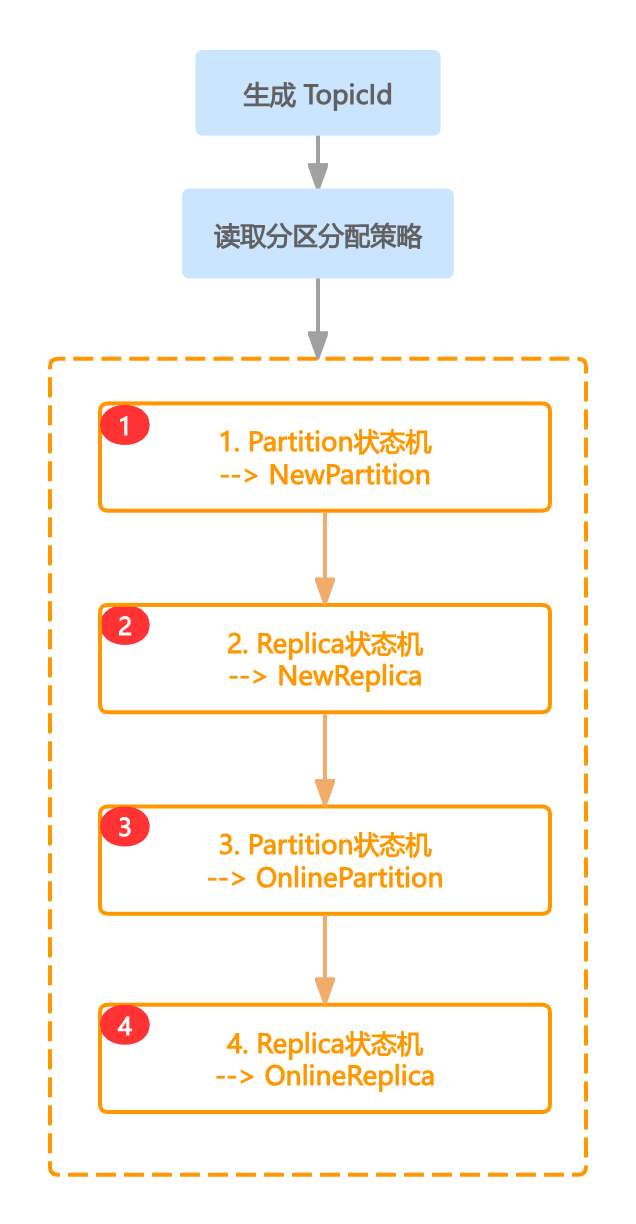
Kafka原理剖析之「Topic创建」
一、前言 Kafka提供了高性能的读写,而这些读写操作均是操作在Topic上的,Topic的创建就尤为关键,其中涉及分区分配策略、状态流转等,而Topic的新建语句非常简单 bash kafka-topics.sh \ --bootstrap-server localhost:9092 \ // …...

Java 高级学习路线概要~
前言:恭喜你已经掌握了 Java 的基础知识!现在,让我们踏上 Java 高级学习之旅,探索更强大的编程技巧和技术。学习前记得不要忘了巩固和加强基础的学习哦,高级学习也是建立在基础的学习之上。 1. 集合框架进阶 Map 接口…...

浏览器插件快速开启/关闭IDM接管下载
假设你已经为浏览器安装了IDM扩展,那么按下图的点击顺序,可以快速开启或关闭IDM的下载接管,而不必在IDM软件的设置->选项中,临时作调整。...

初识c++:入门基础
打字不易,留个赞再走吧~~ 目录 一.第一个c程序二.命名空间 namespace三.C输⼊&输出四.缺省参数 C兼容C语⾔绝⼤多数的语法,所以C语⾔实现的hello world依旧可以运⾏,C中需要把定义⽂件 代码后缀改为.cpp 一.第一个c程序 做好准备我们来写…...

Java Exception 异常相关总结
1.简介 在Java中,当代码运行有问题时会抛出异常,主要分为两类: 1.可以通过try...catch来捕获解决的,不影响后续执行的RuntimeException。 2.不可以通过代码解决的Exception。 为了提高代码的健壮性,我们会选择去捕…...
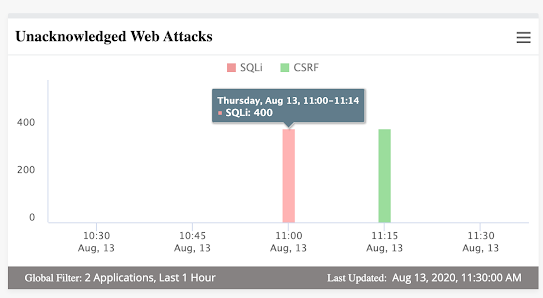
HighCharts图表自动化简介
什么是分析数据? 在任何应用程序中捕获并以图形或图表形式显示的分析数据是任何产品或系统的关键部分,因为它提供了对实时数据的洞察。 验证此类分析数据非常重要,因为不准确的数据可能会在报告中产生问题,并可能影响应用程序/系统的其他相关领域。 什么是HighChart? …...
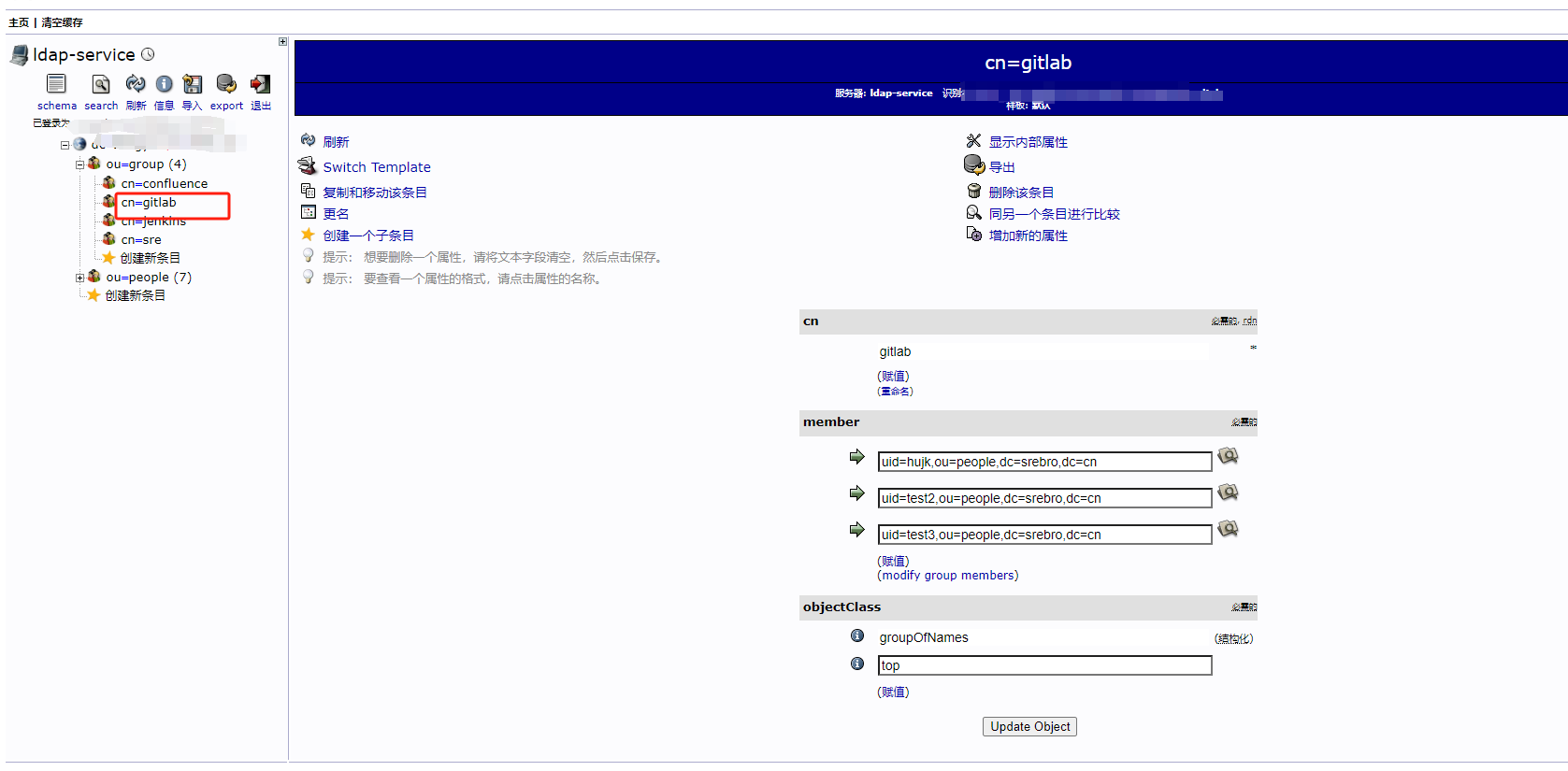
使用LDAP登录GitLab
使用LDAP登录GitLab gitlab.rb 配置如下 gitlab_rails[ldap_enabled] true #gitlab_rails[prevent_ldap_sign_in] false###! **remember to close this block with EOS below** gitlab_rails[ldap_servers] YAML.load <<-EOSmain:label: LDAPhost: 172.16.10.180port:…...

【2024】前端学习笔记5-表单标签使用
表单是网页提供的一种交互式操作手段,主要用于采集用户输入的信息。 学习笔记 1.表单框架:form标签1.1.action属性:目标指向1.2.method属性:提交方式1.3.id属性:唯一标识1.4.placeholder属性:提示文字2.input标签2.1.text类型:基本文本输入2.2.password类型:密码输入2.…...
)
数据结构--二叉树(C语言实现,超详细!!!)
文章目录 二叉树的概念代码实现二叉树的定义创建一棵树并初始化组装二叉树前序遍历中序遍历后序遍历计算树的结点个数求二叉树第K层的结点个数求二叉树高度查找X所在的结点查找指定节点在不在完整代码 二叉树的概念 二叉树(Binary Tree)是数据结构中一种…...

【将字符串变为空的编辑距离】
题目描述 求由s串变成t串的编辑距离 在s串的开头/末尾添加一个字符,花费p 在s串的开头/末尾添加一个s串的子串,花费q 每次作都是基于当前的s串 s串初始为空 分析 等价于将一个字符串变为空串的过程 第一层按照长度遍历(如果按照下标i,j遍…...

卡特兰数的推理
卡特兰数(Catalan number),又称卡塔兰数、明安图数,是组合数学中一种常出现于各种计数问题中的数列。它以比利时数学家欧仁查理卡特兰的名字命名,但值得注意的是,这一数列的首次发现可以追溯到1730年&#…...

高精度治具加工的重要性和优势
在现代工业制造中,高精度治具加工扮演着举足轻重的角色。它不仅关乎产品制造的精度与质量,还直接影响到生产效率和成本控制。因此,时利和将深入探讨高精度治具加工的重要性和优势,对于提升工业制造水平具有重要意义。 高精度治具加…...

新版IDEA提示@Autowired不建议字段注入
随着项目的复杂度的增加,我们通常会在一个业务类中注入其他过多的业务类。从而使当前的业务层扩充成一个大而全的功能模块。那么就容易出现一下问题 字段注入会让依赖关系变得不那么明显,因为你无法通过构造函数看到所有的依赖项。使用构造函数时&#…...

adb的安装和使用 以及安装Frida 16.0.10+雷电模拟器
.NET兼职社区 .NET兼职社区 .NET兼职社区 1.下载adb Windows版本:https://dl.google.com/android/repository/platform-tools-latest-windows.zip 2.配置adb环境变量 按键windowsr打开运行,输入sysdm.cpl,回车。 高级》环境变量》系统变量》…...

解决移动端1px 边框优化的8个方法
前言 您是否注意到 1px 边框在移动设备上有时会显得比预期的要粗?这种不一致源于移动屏幕的像素密度不同。 在 Web 开发中,我们使用 CSS 来设置页面样式。但是,CSS 中的 1px 并不总是转换为设备上的物理 1px。这种差异就是我们的“1px 边框…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...
