“树”据结构:并查集从入门到AC
“树”据结构:并查集
- 前言
- 算法设计
- 代码示例
- 优化
- 相关文章
前言
在一组数据中,数据被分为了不同的集合,那么其中的集合往往可以用树形来表示。而区分集合,与查找集合的元素,就会成为核心的问题。并查集主要就是解决这类问题,因此并查集算法的核心也就是查找与区分。
并查集通过一个一维数组来实现,因此,给我们提供了更大的时间和空间上的便利。通过一维数组来维护一个森林,也就是维护由不同树为子集构成的集合。
问题示例:
有10个学生,1号与2号同班,3号和5号同班,4号和6号同班,7号和3号同班,8号和10号同班,9号和2号同班,8号和4号同班。
然后一般是要求解不同的班级数or输入序号查询同班同学
这类问题都是经典的并查集模板。
算法设计
先动动笔算下我们需要的结果:
1,2,9一个班级
3,5,7一个班级
4,6,8,10一个班级
首先先将一个一维数组初始化,设数组的值为其班级序号,假设每个学生都来自不同的班级,即f[i]=i。
由此f[1]=1,f[2]=2,f[3]=3,…f[10]=10。
然后我们再把结点合并成树,树内部再做处理。
由结点合并为树:以靠左优先进行同班合并,由于输入的条目是1 2,所以2号的2班消失合并到1班

接下来我们要准备的函数是,搜索同班同学的归属,我们先写一个深度搜索:
int dfs(int v)
{if(a[v]==v)return v;else{dfs(a[v]);}
}
于是我们可以搜索到同班同学的最终归属。
而当我们读到输入条目:9号与2号同班的时候,由于2号班级已经消失成为了1号班级(形成了树,而不是单一结点),这时候我们将整个结点归到9号之下:

但这时候我们的算法没有完成,因为在最后的数组下标里,1、2、9明明同属于9班2号学生却属于1班,2向1的指针就多余了,那么我们需要略微处理下搜索算法来处优化冗余数据,也称路径压缩:

如此处理,当最终搜索完成的时候,只要每次存在f[i]=i,就代表了有一个独立的班级,这棵树的最终父节点为i。
代码示例
初始化数据
scanf("%d %d",&n,&m);//输入学生数与数据条目数for(i=0;i<=n;i++){f[i]=i;//初始化}for(i=1;i<=m;i++){scanf("%d %d",&x,&y);//输入每组同班条目Merge_(x,y);//合并函数}
合并函数:
进行同班合并
t1与t2代表了v和u的祖先结点,如果t1与t2不相等,t2从下至上一整支需要归并到t1下
void Merge_(int v,int u)
{int t1=0,t2=0;t1=getf(v);//查找根部归属t2=getf(u);if(t1!=t2){f[t2]=t1;}}
搜索函数只需要在上文的基础上稍稍加强一下
int getf(int v)
{if(f[v]==v)return v;else{f[v]=getf(f[v]);//路径压缩return f[v];}
}
到这里,我们拿上文的题目来做输入输出示例:
有10个学生,1号与2号同班,3号和5号同班,4号和6号同班,7号和3号同班,8号和10号同班,9号和2号同班,8号和4号同班。
求学生来自多少个不同班级
那么用变量 j 来扫描搜索结果:
for(i=1;i<=n;i++){if(f[i]==i){j++;}}

得解分为3个班级。
优化
并查集的优化思路不少,但核心都在于,如何高效的来合并树,也就是谁向谁合并。
通俗的说,既然合并的过程是修改被合并的树的祖先认知,由于修改的过程是把树回溯,那么显然,被合并的树越小,速度就会越快,反之越慢。
前文中我们使用的是向左边的树合并,那么现在我们可以始终保持小树向大树合并:
先去声明一个size数组,来表示树的结点数量,并全部初始化为1
void Merge_(int v,int u)
{int t1=0,t2=0;t1=getf(v);t2=getf(u);if(t1!=t2){if (size[t1] > size[t2]) {//比较大小,然后由小并大f[t2] = t1;size[t1] += size[t2];} else {f[t1] = t2;size[t2] += size[t1];}}}
相关文章
二叉树从入门到AC(1)构建和前中后序遍历
二叉树从入门到AC(2)深度与层次遍历
二叉树从入门到AC(3)完全二叉树与堆
相关文章:

“树”据结构:并查集从入门到AC
“树”据结构:并查集 前言算法设计代码示例优化相关文章 前言 在一组数据中,数据被分为了不同的集合,那么其中的集合往往可以用树形来表示。而区分集合,与查找集合的元素,就会成为核心的问题。并查集主要就是解决这类…...

高级java每日一道面试题-2024年9月11日-数据库篇-事务回滚的常见原因有哪些?
如果有遗漏,评论区告诉我进行补充 面试官: 事务回滚的常见原因有哪些? 我回答: 在Java高级面试中,讨论事务回滚的常见原因是考察候选人对事务管理的理解深度。事务回滚意味着事务中的所有操作都会被撤销,回到事务开始前的状态。以下是事务…...

目标检测中的解耦和耦合、anchor-free和anchor-base
解耦和耦合 写在前面 在目标检测中,objectness(或 objectness score)指的是一个评分,用来表示某个预测框(bounding box)中是否包含一个目标物体。 具体来说,YOLO等目标检测算法需要在每个候选区…...

git rev-parse
git rev-parse 是 Git 中一个非常有用的命令,用于解析并返回与 Git 对象(如提交、分支、标签等)相关的信息。它可以帮助我们从给定的引用(ref)中解析出 SHA-1 哈希值、路径信息等。这个命令在编写 Git 脚本时尤其有用&…...
【Unity】在Unity 3D中使用Spine开发2D动画
文章目录 内容概括前言下载安装 Spine Pro导入Unity插件Spine动画导入Unity使用展现动画效果展现 内容概括 本文主要讲解 Spine Pro 免(破)费(解)版的安装,以及如何将动画导入到Unity中使用。 前言 通常要用 Spine …...

考试:软件工程(01)
软件开发生命周期 ◆软件定义时期:包括可行性研究和详细需求分析过程,任务是确定软件开发工程必须完成的总目标, 具体可分成问题定义、可行性研究、需求分析等。 ◆软件开发时期:就是软件的设计与实现,可分成概要设计…...
——赫夫曼编码)
数据结构应用实例(三)——赫夫曼编码
Content: 一、问题描述二、算法思想三、代码实现四、小结 一、问题描述 对一篇英文文章,统计各字符(仅限于26个小写字母)出现的次数,并据此进行 Huffman 编码。 二、算法思想 首先,打开文本文件࿰…...

关于Spring Cloud Gateway中 Filters的理解
Spring Cloud Gateway中 Filters的理解 Filters Filters拦截器的作用是,对请求进行处理 可以进行流量染色 ⭐增加请求头 例子 spring:cloud:gateway:routes:- id: add_request_header_routeuri: http://localhost:8123predicates:- Path/api/**filters:- AddR…...

【实践】应用访问Redis突然超时怎么处理?
目录标题 问题描述分析过程查看监控数据系统监控指标JVM监控指标Redis监控指标分析应用异常单机异常规律集群异常规律统计超时的key 初步结论验证结论访问Redis链路slowlogRedis单节点info all定位redis节点定位异常keybigkeystcpdump定位大key影响 经验总结 问题描述 某产品线…...

Spring Cloud Alibaba核心组件Nacos/Seata/Sentinel
文章目录 Spring Cloud Alibaba介绍Spring Cloud 微服务体系Spring Cloud Alibaba 定位 注册配置中心--Nacos服务治理架构注册中心原理 Nacos介绍Nacos 的关键特性1.服务注册和发现2.动态配置服务3.实时健康监控4.动态DNS服务5.易于集成: Nacos入门示例服务注册与发…...
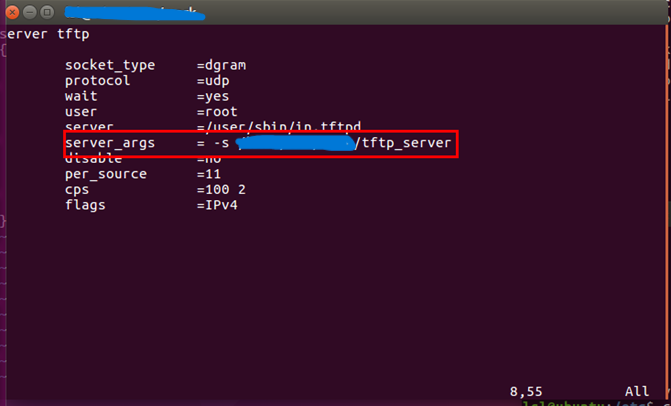
Ubuntu搭建FTP服务器
1. 首先,我们需要安装和配置xinetd,安装的具体命令如下: sudo apt-get install xinetd 2. 新建tftp工作目录,并添加读、写、执行权限(没有权限后面无法正常访问该文件夹),如下图所示。 3. 安装…...

Redis在单线程下删除大Key会发生什么?怎么删除大Key?
大Key的定义 大Key是指在缓存系统(如Redis)或分布式存储中,单个键(Key)对应的数据量非常大,通常存储的是大块数据结构,例如包含大量数据的哈希表、列表、集合或有序集合。这种大Key往往会对系统…...

《Exploit temporal cues in multi-camera 3D object detection》论文泛读
ReadPaperhttps://readpaper.com/pdf-annotate/note?pdfId4666749915775385601eId2491528568128599808 针对单帧数据含有的信息太少的问题,提出了一种新的方法,BEVDet4D,这种方法可以访问时间线索,并且取得了较好的表现ÿ…...

十四、centos7 yum报错:cannot find a valid baseurl for repo:base/7/x86_64的解决方案
🌻🌻目录🌻🌻 一、 centos7 yum报错:cannot find a valid baseurl for repo:base/7/x86_64二、分析错误三、解决方案3.1 检查网络连接3.2 检查DNS设置3.3 检查YUM仓库配置3.3.1 使用官方CentOS镜像配置3.3.2 使用阿里云…...

qt使用对数坐标的例子,qchart用QLogValueAxis坐标不出图解决
硬件:ThinkPad T15 系统:win10 专业版 qt版本:Qt 5.14.1 , QtCreator 4.11.1 软件界面放了一个QPushButton,一个QVBoxLayout,如下: 主要代码如下,我添加了两条曲线,…...

Python 爬虫入门 - 爬虫 requests 请求
在当今互联网时代,数据的获取变得尤为重要,而网络爬虫作为自动化获取数据的一种方式,受到了越来越多编程爱好者和数据分析人员的青睐。Python 语言以其简洁的语法和丰富的库,成为了实现网络爬虫的首选工具。其中,requests库是一个非常流行且强大的工具,用于发送 HTTP 请求…...
 的详解)
flink中startNewChain() 的详解
在 Apache Flink 中,startNewChain() 是一个与算子链(operator chaining)相关的方法。与 disableChaining() 类似,它允许开发者控制算子链的创建方式,但 startNewChain() 的作用是从当前算子开始创建一个新的算子链&am…...

uniapp 苹果安全域适配
一、使用原生占位(仅App端支持) //在manifest.json 文件中 app-plus 中配置 "safearea": { "background": "#FFFFFF", "bottom": { "offset": "auto" } } 二、不使用原生占位 //&…...

linux使用命令行编译qt.cpp
步骤: mkdir qttestcd qttestvim hello.cpp #include <QApplication> #include <QDialog> #include <QLabel> int main(int argc,char* argv[]) {QApplication a(argc,argv);QLabel label("aaa");label.resize(100,100);label.show()…...

Ubuntu 22.04 LTS 上安装 Docker
单台机器安装docker环境,是为了后面安装open-webui,环境安装比较简单,没有难点,但一定要按步骤走,否则还是会遇到一些问题的。 第 1 步:更新软件包并安装必要软件 运行以下命令,更新软件包索引…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...
