图论篇--代码随想录算法训练营第六十一天打卡| Floyd 算法,A*算法
Floyd 算法(求多源汇最短路)
题目链接:97. 小明逛公园
题目描述:
小明喜欢去公园散步,公园内布置了许多的景点,相互之间通过小路连接,小明希望在观看景点的同时,能够节省体力,走最短的路径。
给定一个公园景点图,图中有 N 个景点(编号为 1 到 N),以及 M 条双向道路连接着这些景点。每条道路上行走的距离都是已知的。
小明有 Q 个观景计划,每个计划都有一个起点 start 和一个终点 end,表示他想从景点 start 前往景点 end。由于小明希望节省体力,他想知道每个观景计划中从起点到终点的最短路径长度。 请你帮助小明计算出每个观景计划的最短路径长度。
算法思想:
使用三重for循环,遍历从1~n节点,grip二维数组含义是表示点i和j间的距离,将其初始化为INT_MAX,对角线初始化为0。使用grip[i][j] = min(grip[i][j],grip[i][k]+grip[k][j])来判断最短路径。
代码:
#include<iostream>
#include<vector>
#include<climits>
using namespace std;void floyd(vector<vector<int>>& graphs)
{int n = graphs.size() - 1;for(int k = 1; k <= n; k++)for(int i = 1; i <= n; i++)for(int j = 1; j <= n; j++)if(graphs[i][k] != INT_MAX && graphs[k][j] != INT_MAX)graphs[i][j] = min(graphs[i][j],graphs[i][k] + graphs[k][j]);
}int main()
{int n,m;cin >> n >> m;vector<vector<int>> graphs(n+1,vector<int>(n+1,INT_MAX));for(int i = 1; i <= n; i++) graphs[i][i] = 0;for(int i = 0; i < m; i++){int u,v,w;cin >> u >> v >> w;graphs[u][v] = min(graphs[u][v],w);graphs[v][u] = min(graphs[v][u],w);}floyd(graphs);int q;cin >> q;while(q--){int start,end;cin >> start >> end;if(graphs[start][end] == INT_MAX) cout << -1 << endl;else cout << graphs[start][end] << endl;}return 0;
}A*算法
题目链接:127. 骑士的攻击
题目描述:
在象棋中,马和象的移动规则分别是“马走日”和“象走田”。现给定骑士的起始坐标和目标坐标,要求根据骑士的移动规则,计算从起点到达目标点所需的最短步数。
棋盘大小 1000 x 1000(棋盘的 x 和 y 坐标均在 [1, 1000] 区间内,包含边界)
算法思想:
1、该算法是对宽搜算法的优化,能保证有方向地去搜索点。在宽搜基础上增添了权重概念。
2、如何保证有方向搜索--对每一个点设置一个权重f,f=g+h,g表示起点达到目前遍历节点的距离,h表示目前遍历的节点到达终点的距离。距离计算公式如下:
- 曼哈顿距离,计算方式: d = abs(x1-x2)+abs(y1-y2)
- 欧氏距离(常用,不会超时) ,计算方式:d = (x1-x2)^2 + (y1-y2)^2
- 切比雪夫距离,计算方式:d = max(abs(x1 - x2), abs(y1 - y2))
3、每次使用具有最小权重的点来更新节点位置--->使用优先级队列保存
代码:
#include<iostream>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;int b1,b2;
int dx[8] = {-1,-1,1,1,2,2,-2,-2};
int dy[8] = {2,-2,2,-2,-1,1,-1,1};typedef struct Knight
{int a1,a2;int f,g,h;bool operator < (const struct Knight& k) const{return k.f < f;}
}Knight;int function(const Knight& knt)
{return (knt.a1 - b1)*(knt.a1 - b1) + (knt.a2 - b2)*(knt.a2 - b2);
}void Astar(vector<vector<int>>& step, const Knight& knt, priority_queue<Knight>& pq)
{Knight cur,next;while(!pq.empty()){cur = pq.top(),pq.pop();if(cur.a1 == b1 && cur.a2 == b2) break;for(int i = 0; i < 8; i++){next.a1 = cur.a1 + dx[i];next.a2 = cur.a2 + dy[i];if(next.a1 < 1 || next.a1 > 1000 || next.a2 < 1 || next.a2 > 1000) continue;if(!step[next.a1][next.a2]){step[next.a1][next.a2] = step[cur.a1][cur.a2] + 1;next.g = cur.g + 5;next.h = function(next);next.f = next.g + next.h;pq.push(next);}}}
}int main()
{int a1,a2,n;cin >> n;while(n--){priority_queue<Knight> pq;vector<vector<int>> step(1010,vector<int>(1010));cin >> a1 >> a2 >> b1 >> b2;Knight knt;knt.a1 = a1;knt.a2 = a2;knt.g = 0;knt.h = function(knt);knt.f = knt.g + knt.h;pq.push(knt);Astar(step,knt,pq);cout << step[b1][b2] << endl;}return 0;
}相关文章:

图论篇--代码随想录算法训练营第六十一天打卡| Floyd 算法,A*算法
Floyd 算法(求多源汇最短路) 题目链接:97. 小明逛公园 题目描述: 小明喜欢去公园散步,公园内布置了许多的景点,相互之间通过小路连接,小明希望在观看景点的同时,能够节省体力&…...
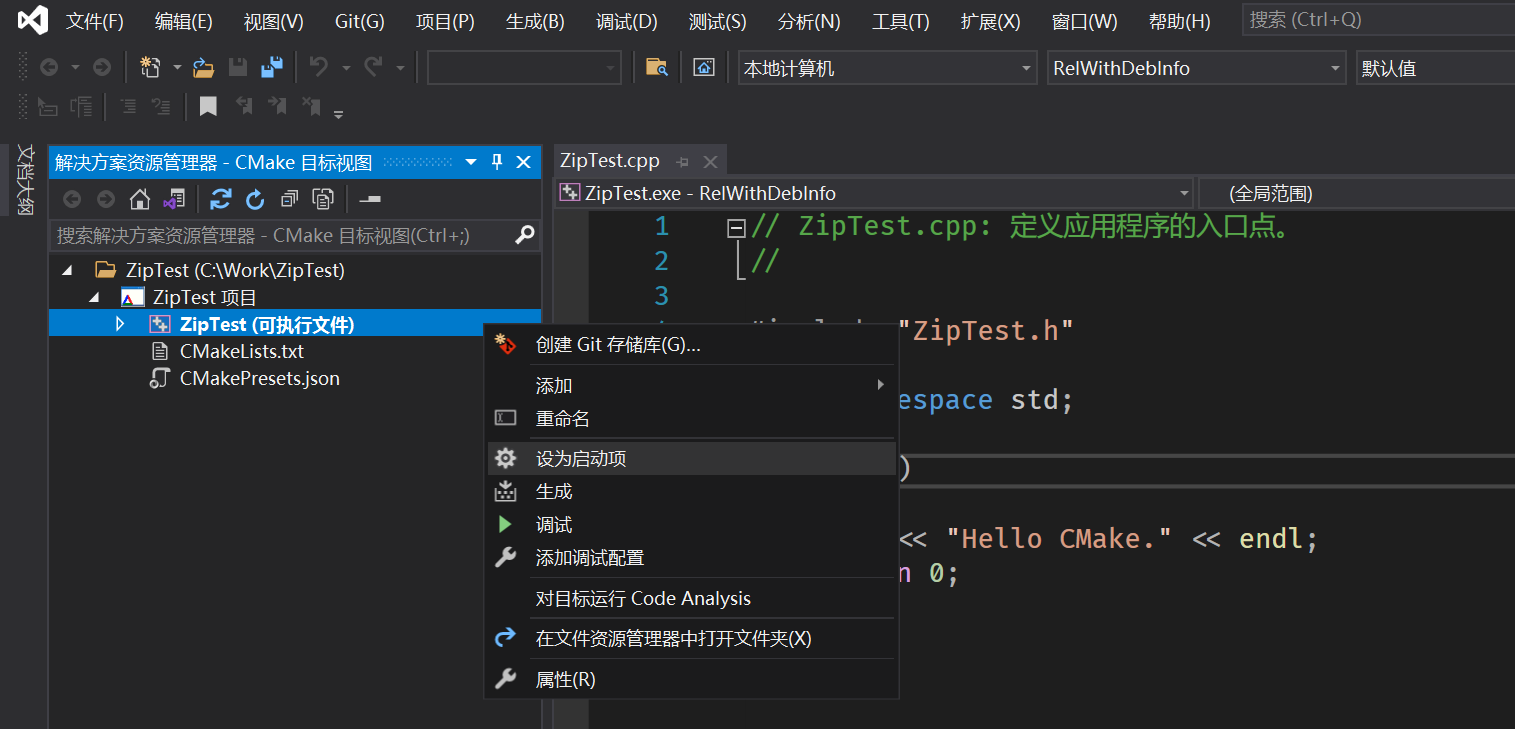
CMake构建学习笔记16-使用VS进行CMake项目的开发
文章目录 1. 概论2. 详论2.1 创建工程2.2 加载工程2.3 配置文件2.4 工程配置2.5 调试执行 3. 项目案例4. 总结 1. 概论 在之前的系列博文中,我们学习了如何构建第三方的依赖库,也学习了如何去组建自己的CMake项目,尤其是学习了CMake的核心配…...

数据结构中线性表的定义和特点
线性表:有n个数据特征相同的元素构成的有限序列。 特点: 除了第一个元素,最后一个元素,其余的元素都有唯一的前驱和唯一的后继。 案例引入: 一元多项式的运算: 可以将一元多项式p(x)抽象为一个有n1个系…...
模块详解)
【PyTorch单点知识】PyTorch中的自动混合精度(AMP)模块详解
文章目录 0. 前言1. 什么是自动混合精度?2. PyTorch AMP 模块3. 如何使用 PyTorch AMP3.1 环境准备3.2 代码实例3.3 代码解析 4. 结论 0. 前言 按照国际惯例,首先声明:本文只是我自己学习的理解,虽然参考了他人的宝贵见解及成果&a…...

数据结构 --- 哈希表
哈希表(Hash Table),也叫散列表,是一种根据关键码值(Key value)而直接进行访问的数据结构。 一、基本原理 哈希函数 哈希表通过一个特定的哈希函数,将关键码映射到表中的一个位置。这个位置通常…...

Linux相关:在阿里云下载centos系统镜像
文章目录 1、镜像站2、下载方式一2.1、第一步打开镜像站地址2.2 下载地址: https://mirrors.aliyun.com/centos/2.3、选择7版本2.4、镜像文件在isos文件夹中2.5、选择合适的版本 3、下载镜像快捷方式 1、镜像站 阿里云镜像站地址 2、下载方式一 2.1、第一步打开镜像站地址 2…...

24. 线模型对象
线模型Line渲染顶点数据 下面代码是把几何体作为线模型Line (opens new window)的参数,你会发现渲染效果是从第一个点开始到最后一个点,依次连成线。 // 线材质对象 const material new THREE.LineBasicMaterial({color: 0xff0000 //线条颜色 }); //…...

EasyExcel 快速入门
目录 一、 EasyExcel简介 官网链接: 代码链接: 二、 EasyExcel快速上手 引入依赖: 设置Excel相关注解 编写对应的监听类: 简单写入数据: 简单读取数据: 不需要使用监听器: 需要使…...

Sparse4D v1
Sparse4D: Multi-view 3D Object Detection with Sparse Spatial-Temporal Fusion Abstract 基于鸟瞰图 (BEV) 的方法最近在多视图 3D 检测任务方面取得了重大进展。与基于 BEV 的方法相比,基于稀疏的方法在性能上落后,但仍然有很多不可忽略的优点。为了…...

速盾:你知道高防 IP 和高防 CDN 的区别吗?
在当今网络安全形势日益严峻的情况下,网站的安全防护成为了企业和个人关注的焦点。高防 IP 和高防 CDN 作为两种常见的网络安全防护手段,被广泛应用于网站的安全防护中。那么,高防 IP 和高防 CDN 有什么区别呢?防护网站哪个更好呢…...

HTML和CSS网页制作成品
HTML和CSS网页制作成品 一、引言 1. 背景介绍 在当今数字化时代,网页已成为信息传递和交流的重要媒介。HTML和CSS作为网页制作的基石,对于构建美观、功能丰富的网站至关重要。本文将详细介绍如何使用HTML和CSS来制作一个网页成品。 2. 目的和重要性 …...

Ai+若依(集成easyexcel实现excel表格增强)
EasyExcel 介绍 官方地址:EasyExcel官方文档 - 基于Java的Excel处理工具 | Easy Excel 官网 Java解析、生成Excel比较有名的框架有Apache poi、jxl。但他们都存在一个严重的问题就是非常的耗内存,poi有一套SAX模式的API可以一定程度的解决一些内存溢出的问题,但POI还是有一…...
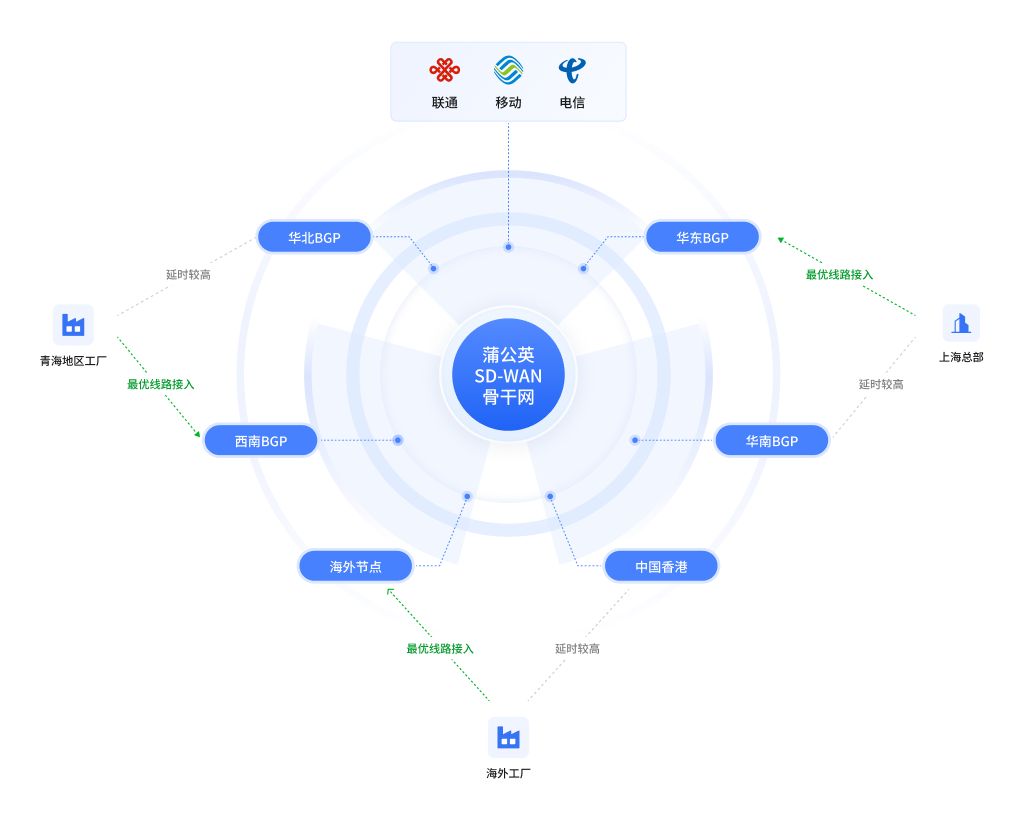
钻机、塔吊等大型工程设备,如何远程维护、实时采集运行数据?
在建筑和工程领域,重型设备的应用不可或缺,无论是在道路与桥梁建设、高层建筑施工,还是在风电、石油等能源项目的开发中,都会用到塔吊、钻机等大型机械工程设备。 随着数字化升级、工业4.0成为行业发展趋势,为了进一步…...

【AutoX.js】选择器 UiSelector - 查找包名
文章目录 原文:https://blog.c12th.cn/archives/38.html选择器 UiSelector - 查找包名笔记直接查找包名双层判断(推荐)查找最外层控件的子控件 最后 原文:https://blog.c12th.cn/archives/38.html 选择器 UiSelector - 查找包名 笔记 AutoX.js UiSelec…...

ERP进销存多仓库管理系统源码 带完整的安装代码包以及搭建部署教程
系统概述 ERP进销存多仓库管理系统是一款专为中小企业量身定制的集成化管理软件,它集成了采购管理、销售管理、库存管理、财务管理以及多仓库协同作业等核心模块。通过统一的平台,企业可以实时掌握商品从入库到出库的全过程,实现库存的自动化…...

数据清洗-缺失值填充-对XGBoost参数优化填充
目录 一、安装所需的python包二、采用XGboost算法进行缺失值填充2.1可直接运行代码2.2以某个缺失值数据进行实战2.2.1 代码运行过程截屏:2.2.2 填充后的数据截屏:三、网格搜索(Grid Search)对 XGBoost 模型的超参数进行优化原理介绍3.1 说明3.2 参数优化的原理1. 网格搜索(…...

Qt_按钮类控件
目录 1、QAbstractButton 2、设置带图标的按钮 3、设置带有快捷键的按钮 4、QRadioButtion(单选按钮) 4.1 QButtonGroup 5、QCheckBox 结语 前言: 按钮类控件是Qt中最重要的控件类型之一,该类型的控件可以通过鼠标的点击…...

union 的定义和基本结构以及用途
在 C 语言中,union(联合体) 是一种数据结构,它允许多个成员共享相同的内存空间。换句话说,联合体中的所有成员都存储在同一块内存区域,不同的成员会占用相同的内存地址,但在同一时刻只能保存一个…...

混合整数规划及其MATLAB实现
目录 引言 混合整数规划的基本模型 混合整数规划的求解方法 MATLAB中的混合整数规划实现 示例:多变量系统的混合整数规划 表格总结:混合整数规划的求解方法与适用场景 结论 引言 混合整数规划(Mixed Integer Programming, MIP…...

【数据结构】6——图1,概念
数据结构6——图1,概念 文章目录 数据结构6——图1,概念基本概念图的分类图的表示方法 基本概念 由 顶点(Vertex) 和 边(Edge) 组成的集合。顶点表示图中的点,而边表示顶点之间的连接。记为 G …...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...

LTR-381RGB-01RGB+环境光检测应用场景及客户类型主要有哪些?
RGB环境光检测 功能,在应用场景及客户类型: 1. 可应用的儿童玩具类型 (1) 智能互动玩具 功能:通过检测环境光或物体颜色触发互动(如颜色识别积木、光感音乐盒)。 客户参考: LEGO(乐高&#x…...
