9. 什么是 Beam Search？深入理解模型生成策略

是不是总感觉很熟悉？
在之前第5，7，8篇文章中，我们都曾经用到过与它相关的参数，而对于早就有着实操经验的同学们，想必见到的更多。这篇文章将从示例到数学原理和代码带你进行理解。

Beam Search 对应的中文翻译为“集束搜索”或“束搜索”。你可以将其当作是贪心算法的拓展，其实是很简单的概念：贪心算法每次只选择最好的，而 Beam Search 会在多个候选中进行选择。通过这篇文章，你将了解到：

• Beam Width（束宽） 的实际作用，常对应于参数名 num_beams。
• 所有候选序列生成结束标记 的含义，常对应于参数名 early_stopping。
• Beam Search 的基本原理和工作机制。

强烈建议访问：Beam Search Visualizer，这是一个非常 Amazing 的交互式项目，在即将完成这个文章攥写的时候我通过官方文档发现了它，让理论与实际搭上了桥。
计划后续补上数学和与其他一些算法的比较。

Beam Search 的基本概念

Beam Search 是一种宽度优先搜索算法，通过保留多个候选序列（即“束”）来探索可能的输出空间。不同于贪心搜索（Greedy Search）每次只选择当前最优的一个候选序列，Beam Search 可以同时保留多个（由束宽 $k$ 决定），从而减少陷入局部最优解的风险。

Beam Search 的工作原理

Beam Search 的核心思想是在每一步生成过程中，保留束宽 $k$ 个最有可能的候选序列，而不是仅保留一个最优序列（这种是贪心算法，也就是说束宽 $k$ 为 1 的时候 Beam Search 就是 Greedy Search）。以下是 Beam Search 的基本步骤：

1. 初始化：从一个初始序列（通常为空或特殊起始标记）开始，设定束宽 $k$，初始化候选序列集 B 0 = { start } B_0 = \{ \text{start} \} B0​={start}。
2. 迭代生成：对于当前所有候选序列 $B_{t-1}$，扩展一个新的词汇或符号，生成所有可能的下一个词汇组合，并计算每个序列的概率。
3. 选择顶束：从所有扩展的候选序列中，选择得分最高的 $k$ 个序列，作为下一步的候选序列 $B_t$。
4. 终止条件：当所有候选序列都生成了结束标记（如 <eos>）或达到设定的最大长度 $T$ 时，停止生成。
5. 选择最终序列：从最终的候选序列集中，选择得分最高的序列作为输出。

注：以GPT为例，扩展实际对应于去获取 tokens 的概率。

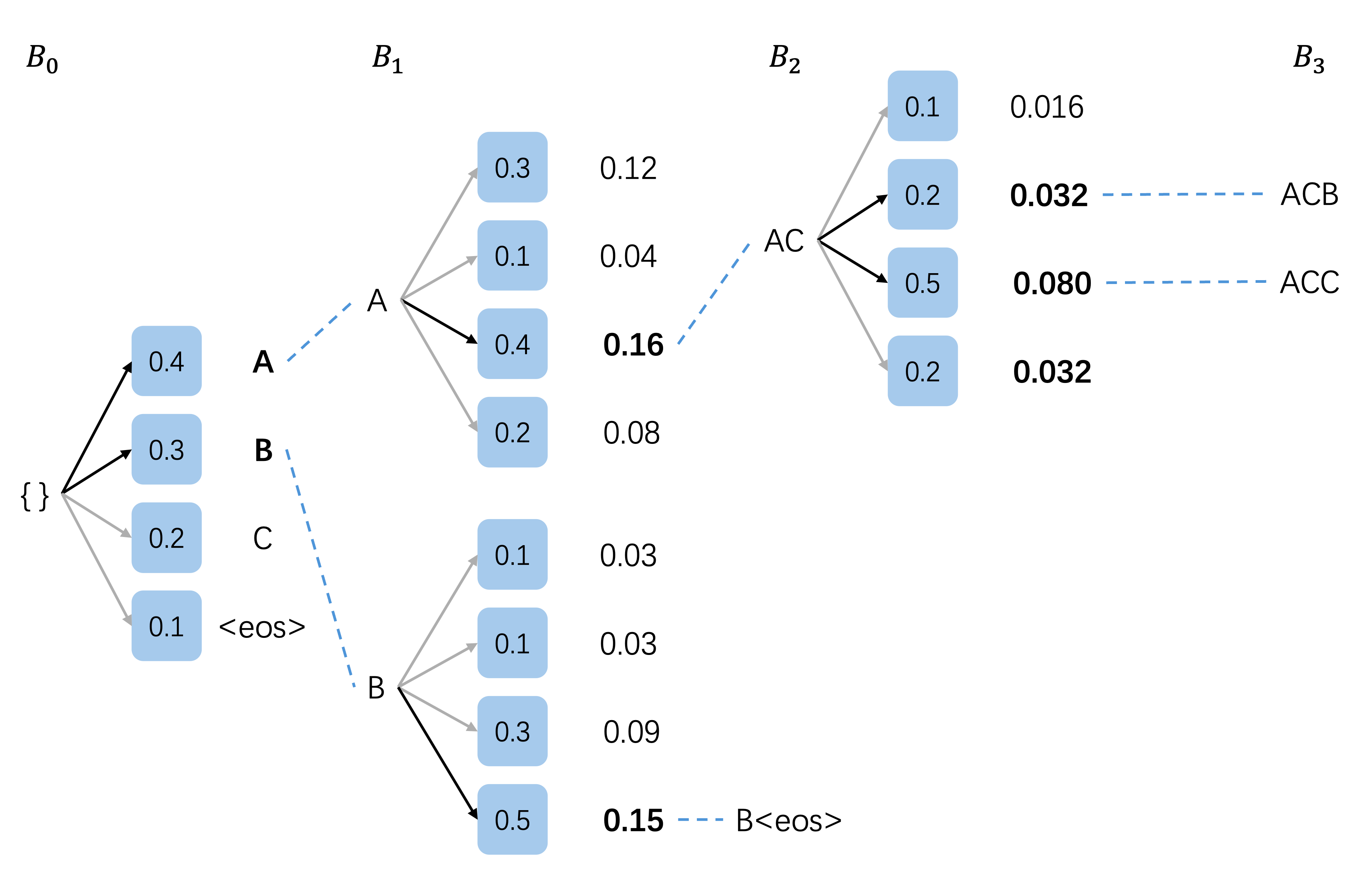
举个例子

1. 初始化

   • 束宽 ($k$): 2
   • 当前候选集 ($B_0$): { （空） } \{\text{（空）}\} {（空）}
   • 词汇表 { A , B , C , ‘<eos>‘ } \{A, B, C, \text{`<eos>`}\} {A,B,C,‘<eos>‘}
   • 扩展（生成所有可能的下一个词汇）：

     扩展结果	概率
     A	$\text{0.4}$
     B	$\text{0.3}$
     C	$0.2$
     <eos>	$0.1$

   • 选择顶束 ($k=2$):
     • $A$（$0.4$）
     • $B$（$0.3$）
   • 新的候选集 ($B_1$): { A ( 0.4 ) , B ( 0.3 ) } \{A (0.4), B (0.3)\} {A(0.4),B(0.3)}

2. 扩展 $A$ 和 $B$

   • 扩展 $A$：

     • 生成概率: { A : 0.3 , B : 0.1 , C : 0.4 , ‘<eos>‘ : 0.2 } \{A: 0.3, B: 0.1, C: 0.4, \text{`<eos>`}: 0.2\} {A:0.3,B:0.1,C:0.4,‘<eos>‘:0.2}

     扩展结果	概率计算	概率
     $AA$	$0.4\times 0.3$	$\text{0.12}$
     $AB$	$0.4\times 0.1$	$0.04$
     $AC$	$0.4\times 0.4$	$\text{0.16}$
     $A\text{<eos>}$	$0.4\times 0.2$	$0.08$

   • 扩展 $B$：

     • 生成概率: { A : 0.1 , B : 0.1 , C : 0.3 , ‘<eos>‘ : 0.5 } \{A: 0.1, B: 0.1, C: 0.3, \text{`<eos>`}: 0.5\} {A:0.1,B:0.1,C:0.3,‘<eos>‘:0.5}

     扩展结果	概率计算	概率
     $BA$	$0.3\times 0.1$	$0.03$
     $BB$	$0.3\times 0.1$	$0.03$
     $BC$	$0.3\times 0.3$	$\text{0.09}$
     $B\text{<eos>}$	$0.3\times 0.5$	$\text{0.15}$

   • 所有扩展序列及其概率：

     序列	概率
     $AC$	$\text{0.16}$
     $AA$	$0.12$
     $B\text{<eos>}$	$\text{0.15}$
     $BC$	$0.09$
     $A\text{<eos>}$	$0.08$
     $AB$	$0.04$
     $BA$	$0.03$
     $BB$	$0.03$

   • 选择顶束 ($k=2$):

     • $AC$（$0.16$）
     • $B\text{<eos>}$（$0.15$）

   • 新的候选集 ($B_2$): { A C ( 0.16 ) , B <eos> ( 0.15 ) } \{AC (0.16), B\text{<eos>} (0.15)\} {AC(0.16),B<eos>(0.15)}

3. 仅扩展 $AC$

   • 生成概率: { A : 0.1 , B : 0.2 , C : 0.5 , ‘<eos>‘ : 0.2 } \{A: 0.1, B: 0.2, C: 0.5, \text{`<eos>`}: 0.2\} {A:0.1,B:0.2,C:0.5,‘<eos>‘:0.2}

   扩展结果	概率计算	概率
   $ACA$	$0.16\times 0.1$	$0.016$
   $ACB$	$0.16\times 0.2$	$0.032$
   $ACC$	$0.16\times 0.5$	$0.080$
   $AC\text{<eos>}$	$0.16\times 0.2$	$0.032$

   • 由于 $B\text{<eos>}$ 已完成，我们选择扩展结果中的顶束：
     • $ACC$（$0.064$）
     • 以某种规则选择 $ACB$ 或 $AC\text{<eos>}$（$0.032$）
   • 新的候选集 ($B_3$): { A C C ( 0.064 ) , A C B ( 0.032 ) } \{ACC (0.064), ACB (0.032)\} {ACC(0.064),ACB(0.032)}

4. 后续步骤

   • 继续扩展：重复上述过程，直到所有候选序列都生成了 <eos> 或达到设定的最大长度。

现在是你访问它的最好时机：Beam Search Visualizer

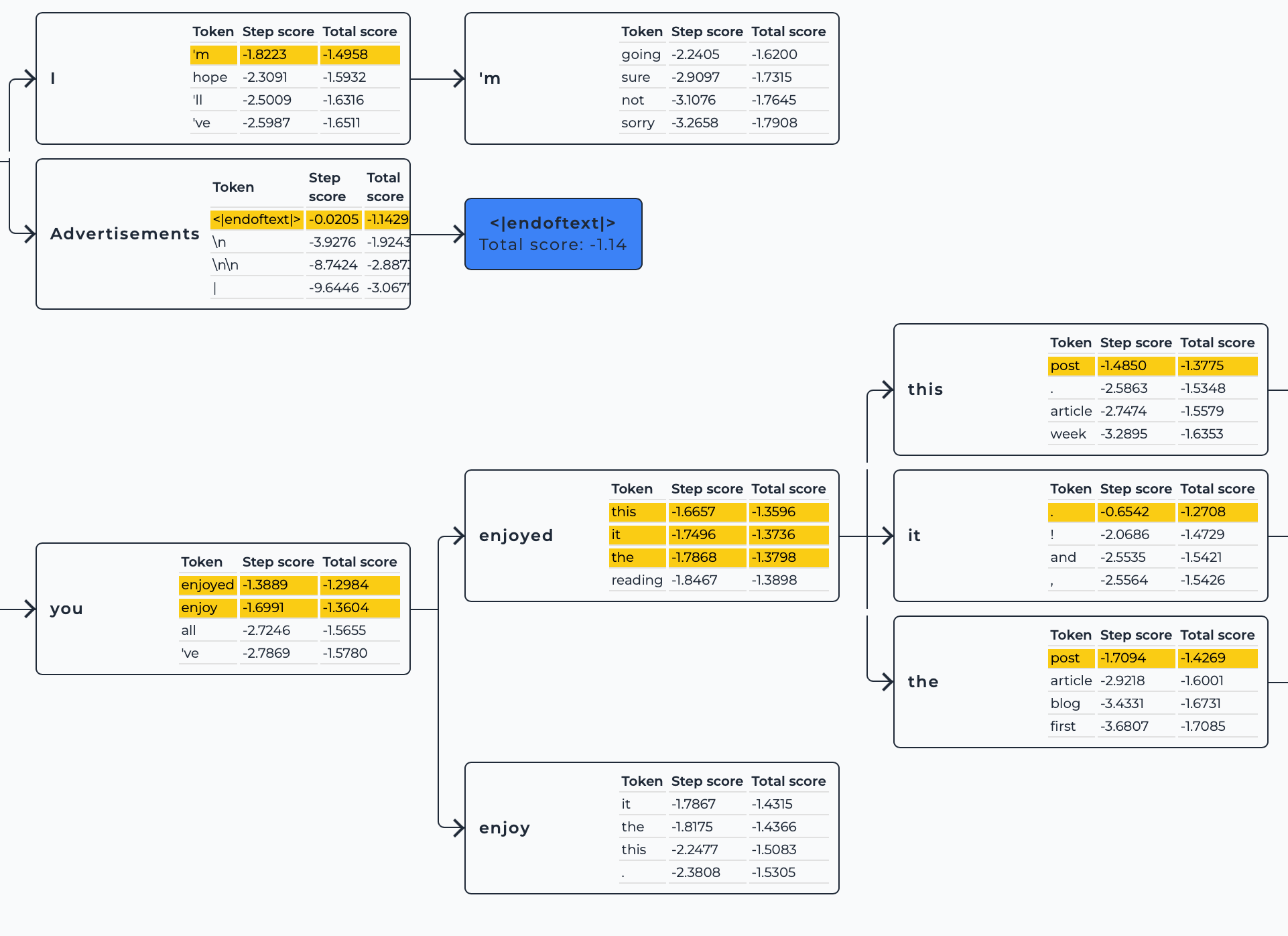
处理 <eos> 的逻辑

在每一步生成过程中，如果某个序列生成了 <eos>，则将其标记为完成，不再进行扩展。以下是处理 <eos> 的示例：

• 假设在某一步，序列 $ACB$ 扩展出 $ACB\text{<eos>}$（$0.032\times 1=0.032$），则：
  • $ACB\text{<eos>}$ 保留在最终候选集，但不再扩展。
  • Beam Search 继续扩展其他未完成的序列，直到所有序列完成或达到最大长度。

问题：如果有一个序列被标记为完成（生成了 <eos>），在下一个扩展步骤中，Beam Search 应该扩展多少个候选序列？

答：束宽 $k$ 个

示例图（k=3）：

你可以在下图中看到，即便有一个序列生成了 <eos>，下一个扩展步骤中还是会扩展 k=3 个候选序列。

实际应用中的 Beam Search

在机器翻译，文本生成，语音转识别等生成式模型领域，你都能看见Beam Search，它被广泛地应用。

代码示例

使用 Hugging Face Transformers 库的简单示例：

from transformers import AutoTokenizer, AutoModelForCausalLM
import torch# 指定模型名称
model_name = "distilgpt2"# 加载分词器和模型
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = AutoModelForCausalLM.from_pretrained(model_name)# 移动模型到设备
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model.to(device)# 设置模型为评估模式
model.eval()# 输入文本
input_text = "Hello GPT"# 编码输入文本
inputs = tokenizer.encode(input_text, return_tensors="pt").to(device)# 生成文本，使用 Beam Search
beam_width = 5
with torch.no_grad():outputs = model.generate(inputs,max_length=50,num_beams=beam_width,  # 你可以看到 beam_width 对应的参数名为 num_beamsno_repeat_ngram_size=2,early_stopping=True  # 开启 early_stopping，当所有候选序列生成<eos>停止)# 解码生成的文本
generated_text = tokenizer.decode(outputs[0], skip_special_tokens=True)
print("生成的文本：")
print(generated_text)

输出：

生成的文本：
Hello GPT.This article was originally published on The Conversation. Read the original article.

对比不同束宽的输出

# 输入文本
input_text = "Hello GPT"# 编码输入文本
inputs = tokenizer.encode(input_text, return_tensors="pt").to(device)# 设置束宽不同的生成策略
beam_widths = [1, 3, 5]  # 使用不同的束宽# 生成并打印结果
for beam_width in beam_widths:with torch.no_grad():outputs = model.generate(inputs,max_length=50,num_beams=beam_width,  no_repeat_ngram_size=2,early_stopping=True,)generated_text = tokenizer.decode(outputs[0], skip_special_tokens=True)print(f"束宽 {beam_width} 的生成结果：")print(generated_text)print('-' * 50)

束宽 1 的生成结果：
Hello GPT is a free and open source software project that aims to provide a platform for developers to build and use GPGP-based GPSP based GPCs. GPP is an open-source software development platform that is designed to
--------------------------------------------------
束宽 3 的生成结果：
Hello GPT.This article is part of a series of articles on the topic, and will be updated as more information becomes available.
--------------------------------------------------
束宽 5 的生成结果：
Hello GPT.This article was originally published on The Conversation. Read the original article.
--------------------------------------------------

参考链接

• Beam-search decoding
• Beam Search Visualizer