稀疏矩阵(Sparse Matrix)
1.背景
在数据科学和深度学习等领域常会采用矩阵格式来存储数据,但当矩阵较为庞大且非零元素较少时, 如果依然使用dense的矩阵进行存储和计算将是极其低效且耗费资源的。所以,通常我们采用Sparse稀疏矩阵的方式来存储矩阵,提高存储和运算效率。下面将对SciPy中七种常见的存储方式(COO/ CSR/ CSC/ BSR/ DOK/ LIL/ DIA)的概念和用法进行介绍和对比总结。
2.稀疏矩阵简介
2.1 稀疏矩阵
- 稀疏矩阵
- 在数值分析中,是其元素大部分为零的矩阵。
- 在矩阵中,若数值0的元素数目远多于非0元素的数目,并且非0元素分布没有规律
- 矩阵的稠密度
- 非零元素的总数比上矩阵所有元素的总数。

- 非零元素的总数比上矩阵所有元素的总数。
2.2 压缩存储
存储矩阵的一般方法是采用二维数组,其优点是可以随机地访问每一个元素,因而能够容易实现矩阵的各种运算, 如转置运算、加法运算、乘法运算等。
对于稀疏矩阵,它通常具有很大的维度,有时甚大到整个矩阵(零元素)占用了绝大部分内存。
采用二维数组的存储方法既浪费大量的存储单元来存放零元素,又要在运算中浪费大量的时间来进行零元素的无效运算。因此必须考虑对稀疏矩阵进行压缩存储(只存储非零元素)。
from scipy import sparse
help(sparse)'''
Sparse Matrix Storage Formats
There are seven available sparse matrix types:1. csc_matrix: Compressed Sparse Column format2. csr_matrix: Compressed Sparse Row format3. bsr_matrix: Block Sparse Row format4. lil_matrix: List of Lists format5. dok_matrix: Dictionary of Keys format6. coo_matrix: Coordinate format (aka IJV, triplet format)7. dia_matrix: Diagonal format8. spmatrix: Sparse matrix base clas
'''
其中一般较为常用的是csc_matrix,csr_matrix和coo_matrix。
2.3 矩阵属性
from scipy.sparse import csr_matrix### 共有属性
mat.shape # 矩阵形状
mat.dtype # 数据类型
mat.ndim # 矩阵维度
mat.nnz # 非零个数
mat.data # 非零值, 一维数组### COO 特有的
coo.row # 矩阵行索引
coo.col # 矩阵列索引### CSR\CSC\BSR 特有的
bsr.indices # 索引数组
bsr.indptr # 指针数组
bsr.has_sorted_indices # 索引是否排序
bsr.blocksize # BSR矩阵块大小
2.4 通用方法
import scipy.sparse as sp### 转换矩阵格式
tobsr()、tocsr()、to_csc()、to_dia()、to_dok()、to_lil()
mat.toarray() # 转为array
mat.todense() # 转为dense
# 返回给定格式的稀疏矩阵
mat.asformat(format)
# 返回给定元素格式的稀疏矩阵
mat.astype(t) ### 检查矩阵格式
issparse、isspmatrix_lil、isspmatrix_csc、isspmatrix_csr
sp.issparse(mat)### 获取矩阵数据
mat.getcol(j) # 返回矩阵列j的一个拷贝,作为一个(mx 1) 稀疏矩阵 (列向量)
mat.getrow(i) # 返回矩阵行i的一个拷贝,作为一个(1 x n) 稀疏矩阵 (行向量)
mat.nonzero() # 非0元索引
mat.diagonal() # 返回矩阵主对角元素
mat.max([axis]) # 给定轴的矩阵最大元素### 矩阵运算
mat += mat # 加
mat = mat * 5 # 乘
mat.dot(other) # 坐标点积resize(self, *shape)
transpose(self[, axes, copy])
3.稀疏矩阵的分类
3.1 COO-coo_matrix
3.1.1Coordinate Matrix 对角存储矩阵
定义详解
- 采用三元组(row, col, data)(或称为ijv format)的形式来存储矩阵中非零元素的信息 ;
- 三个数组 row 、col 和 data 分别保存非零元素的行下标、列下标与值(一般长度相同 );
- 故 coo[row[k]][col[k]] = data[k] ,即矩阵的第 row[k] 行、第 col[k] 列的值为 data[k]

- 当
row[0] = 1,column[0] = 1时,data[0] = 2,故coo[1][1] = 2- 当
row[3] = 0,column[3] = 2时,data[3] = 9,故coo[0][3] = 9
3.1.2 应用场景
- 主要用来创建矩阵,因为coo_matrix无法对矩阵的元素进行增删改等操作
- 一旦创建之后,除了将之转换成其它格式的矩阵,几乎无法对其做任何操作和矩阵运算
3.1.3 优缺点
优点:
- 转换成其它存储格式很快捷简便(
tobsr()、tocsr()、to_csc()、to_dia()、to_dok()、to_lil())- 能与CSR / CSC格式的快速转换
- 允许重复的索引(例如在1行1列处存了值2.0,又在1行1列处存了值3.0,则转换成其它矩阵时就是2.0+3.0=5.0)
缺点:
- 不支持切片和算术运算操作
- 如果稀疏矩阵仅包含非0元素的对角线,则对角存储格式(DIA)可以减少非0元素定位的信息量
- 这种存储格式对有限元素或者有限差分离散化的矩阵尤其有效
3.1.4 实例化
coo_matrix(D):D代表密集矩阵;coo_matrix(S):S代表其他类型稀疏矩阵;coo_matrix((M, N), [dtype]):构建一个shape为M*N的空矩阵,默认数据类型是d;coo_matrix((data, (i, j)), [shape=(M, N)])):三元组初始化i[:]: 行索引j[:]: 列索引A[i[k], j[k]]=data[k]
4.1.5 特殊属性
data:稀疏矩阵存储的值,是一个一维数组row:与data同等长度的一维数组,表征data中每个元素的行号col:与data同等长度的一维数组,表征data中每个元素的列号
4.1.6 案例演示
# 数据
row = [0, 1, 2, 2]
col = [0, 1, 2, 3]
data = [1, 2, 3, 4]# 生成coo格式的矩阵
# <class 'scipy.sparse.coo.coo_matrix'>
coo_mat = sparse.coo_matrix((data, (row, col)), shape=(4, 4), dtype=np.int)# coordinate-value format
print(coo)
'''
(0, 0) 1
(1, 1) 2
(2, 2) 3
(3, 3) 4
'''# 查看数据
coo.data
coo.row
coo.col# 转化array
# <class 'numpy.ndarray'>
coo_mat.toarray()
'''
array([[1, 0, 0, 0],[0, 2, 0, 0],[0, 0, 3, 4],[0, 0, 0, 0]])
'''
3.2 CSR - csr_matrix
3.2.1 Compressed Sparse Row Matrix 压缩稀疏行格式
- csr_matrix是按行对矩阵进行压缩的;
- 通过
indices,indptr,data来确定矩阵。 data表示矩阵中的非零数据- 对于第
i行而言,该行中非零元素的列索引为indices[indptr[i]:indptr[i+1]] - 可以将
indptr理解成利用其自身索引i来指向第i行元素的列索引 - 根据
[indptr[i]:indptr[i+1]],就得到该行中的非零元素个数,如- 若
index[i] = 3且index[i+1] = 3,则第i行的没有非零元素 - 若
index[j] = 6且index[j+1] = 7,则第j行的非零元素的列索引为indices[6:7]
- 若
- 得到了行索引、列索引,相应的数据存放在:
data[indptr[i]:indptr[i+1]]
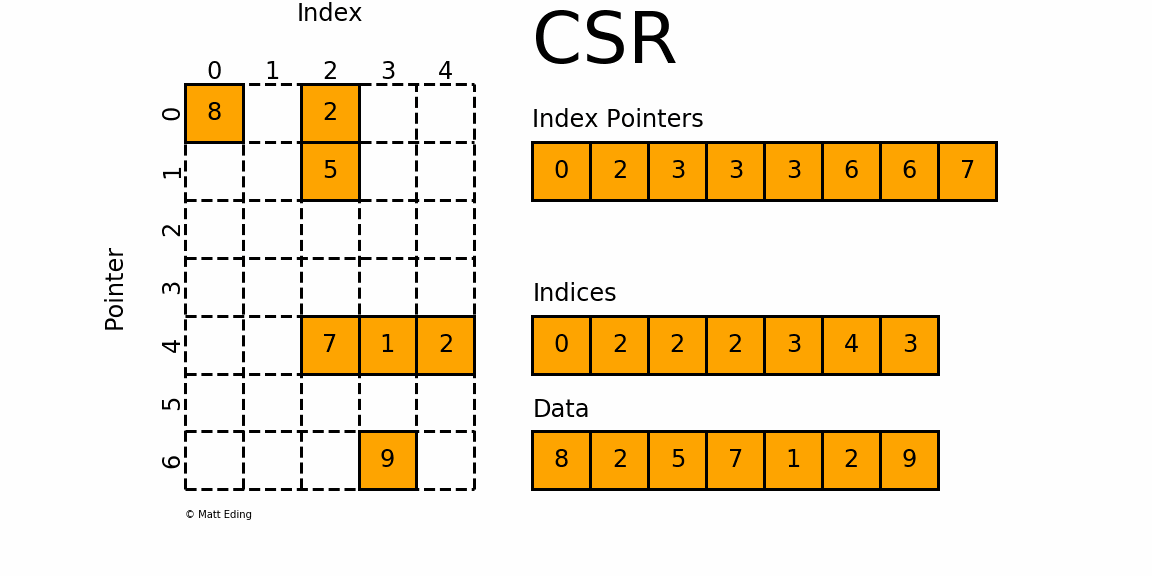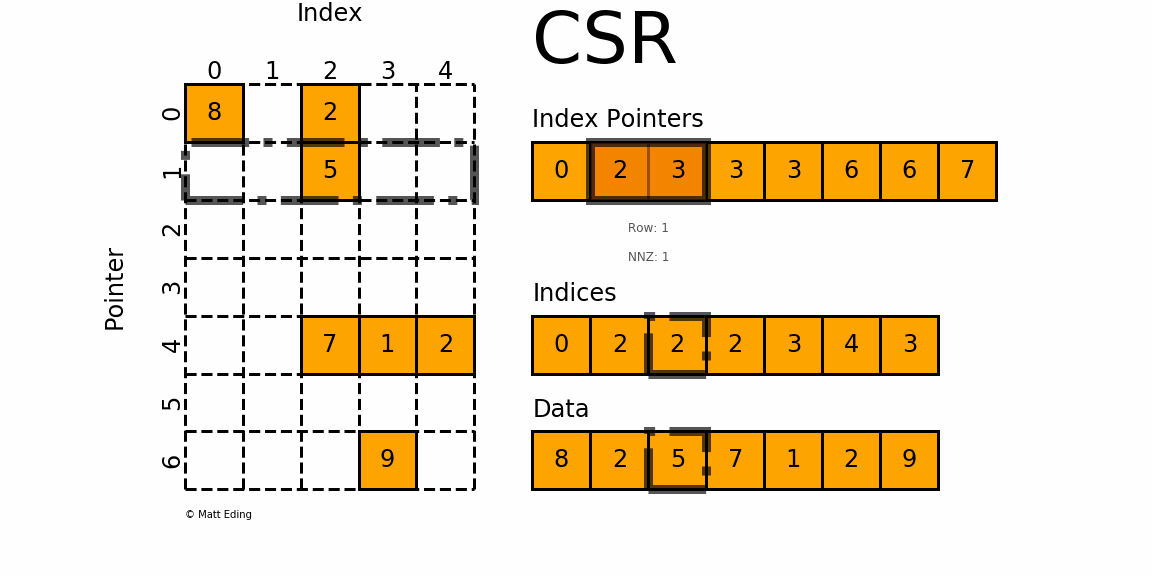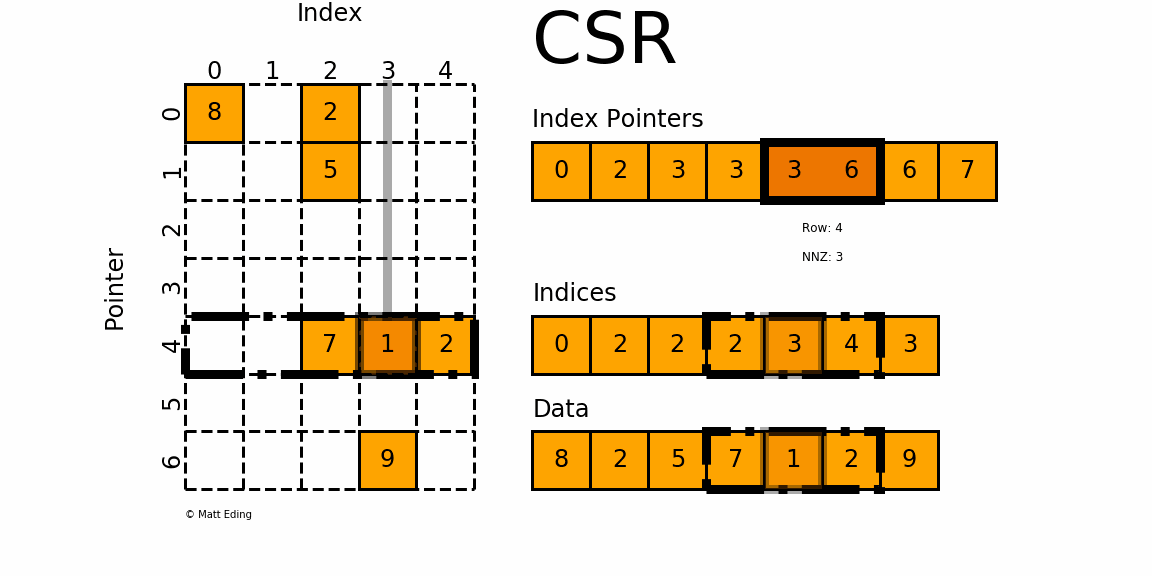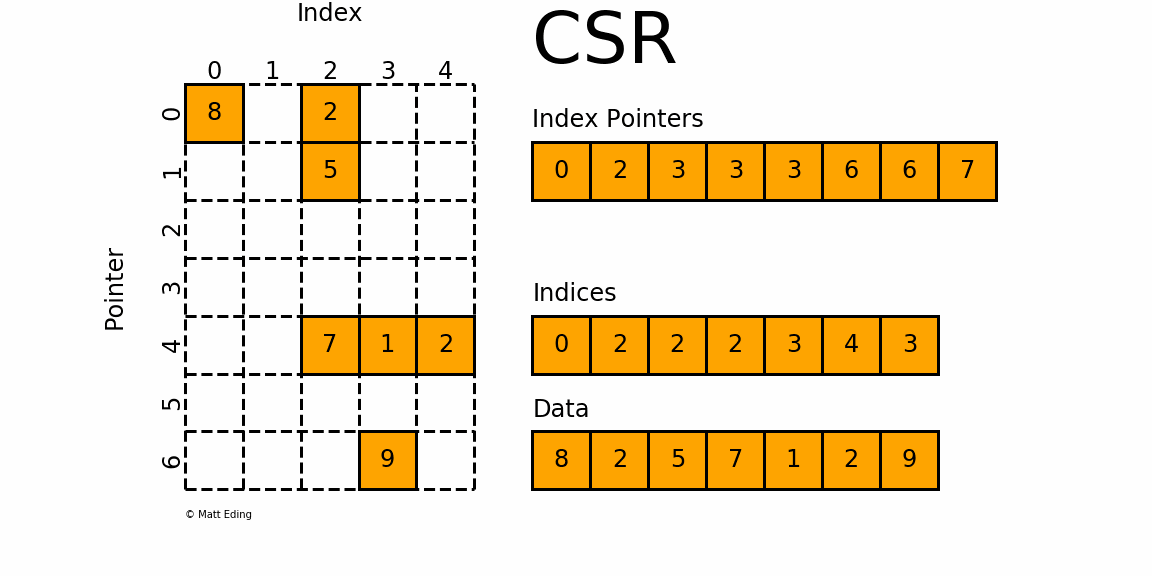
- 对于矩阵第0行,需要先得到其非零元素列索引
- 由
indptr[0] = 0和indptr[1] = 2可知,第0行有两个非零元素。 - 它们的列索引为
indices[0:2] = [0, 2],且存放的数据为data[0] = 8,data[1] = 2 - 因此矩阵第
0行的非零元素csr[0][0] = 8和csr[0][2] = 2
- 由
- 对于矩阵第4行,同样需要先计算其非零元素列索引
- 由
indptr[4] = 3和indptr[5] = 6可知,第4行有3个非零元素。 - 它们的列索引为
indices[3:6] = [2, 3,4],且存放的数据为data[3] = 7,data[4] = 1,data[5] = 2 - 因此矩阵第
4行的非零元素csr[4][2] = 7,csr[4][3] = 1和csr[4][4] = 2
- 由
3.2.2 适用场景
常用于读入数据后进行稀疏矩阵计算,运算高效
3.2.3 优缺点
优点:
- 高效的稀疏矩阵算术运算
- 高效的行切片
- 快速地矩阵矢量积运算
缺点:
- 较慢地列切片操作(可以考虑CSC)
- 转换到稀疏结构代价较高(可以考虑LIL,DOK)
3.2.4 实例化
csr_matrix(D):D代表密集矩阵;csr_matrix(S):S代表其他类型稀疏矩阵csr_matrix((M, N), [dtype]):构建一个shape为M*N的空矩阵,默认数据类型是d,csr_matrix((data, (row_ind, col_ind)), [shape=(M, N)]))- 三者关系:
a[row_ind[k], col_ind[k]] = data[k]
- 三者关系:
csr_matrix((data, indices, indptr), [shape=(M, N)])- 第i行的列索引存储在其中
indices[indptr[i]:indptr[i+1]] - 其对应值存储在中
data[indptr[i]:indptr[i+1]]
- 第i行的列索引存储在其中
3.2.5 特殊属性
data:稀疏矩阵存储的值,一维数组indices:存储矩阵有有非零值的列索引indptr:类似指向列索引的指针数组[has_sorted_indices]: 索引indices是否排序
3.2.6 案例演示
# 生成数据
indptr = np.array([0, 2, 3, 3, 3, 6, 6, 7])
indices = np.array([0, 2, 2, 2, 3, 4, 3])
data = np.array([8, 2, 5, 7, 1, 2, 9])# 创建矩阵
csr = sparse.csr_matrix((data, indices, indptr))# 转为array
csr.toarray()
'''
array([[1, 0, 2],[0, 0, 3],[4, 5, 6]])
'''
# 按row行来压缩
# 对于第i行,非0数据列是indices[indptr[i]:indptr[i+1]] 数据是data[indptr[i]:indptr[i+1]]
# 在本例中
# 第0行,有非0的数据列是indices[indptr[0]:indptr[1]] = indices[0:2] = [0,2]
# 数据是data[indptr[0]:indptr[1]] = data[0:2] = [1,2],所以在第0行第0列是1,第2列是2
# 第1行,有非0的数据列是indices[indptr[1]:indptr[2]] = indices[2:3] = [2]
# 数据是data[indptr[1]:indptr[2] = data[2:3] = [3],所以在第1行第2列是3
# 第2行,有非0的数据列是indices[indptr[2]:indptr[3]] = indices[3:6] = [0,1,2]
# 数据是data[indptr[2]:indptr[3]] = data[3:6] = [4,5,6],所以在第2行第0列是4,第1列是5,第2列是6
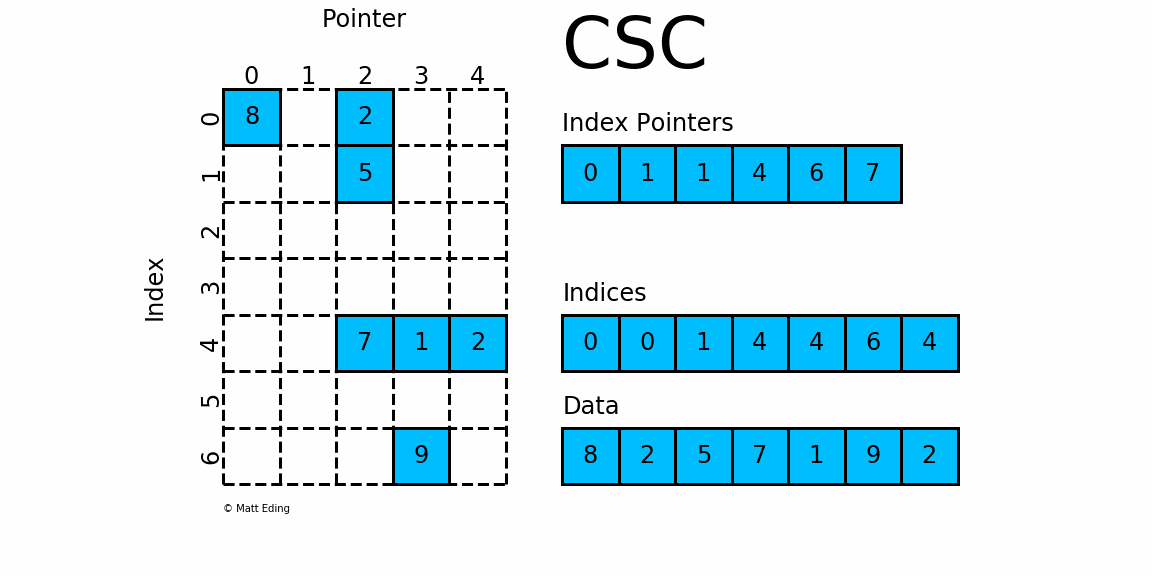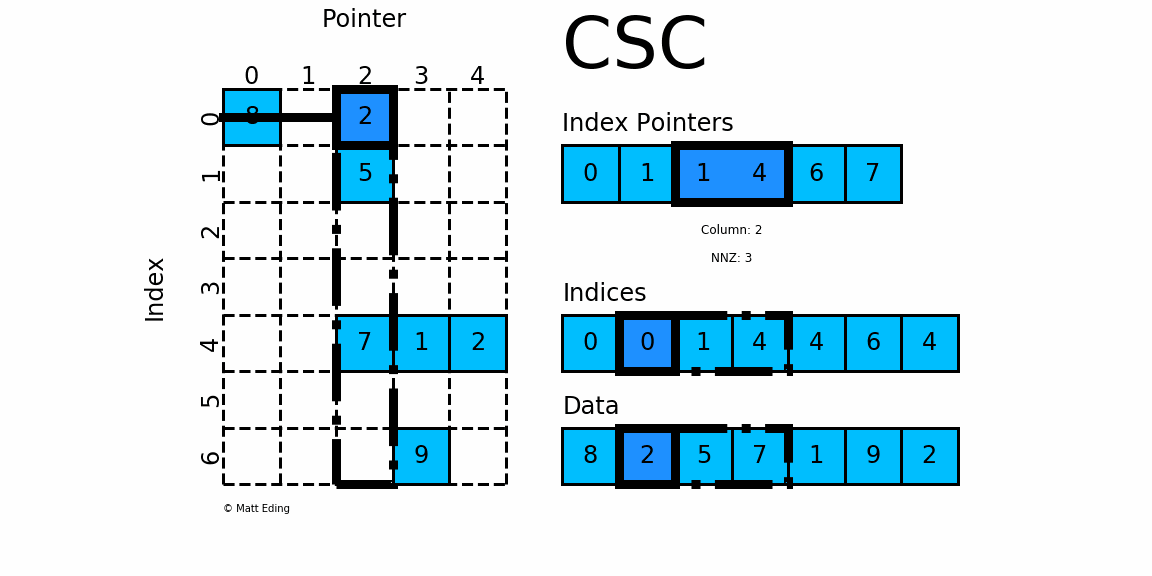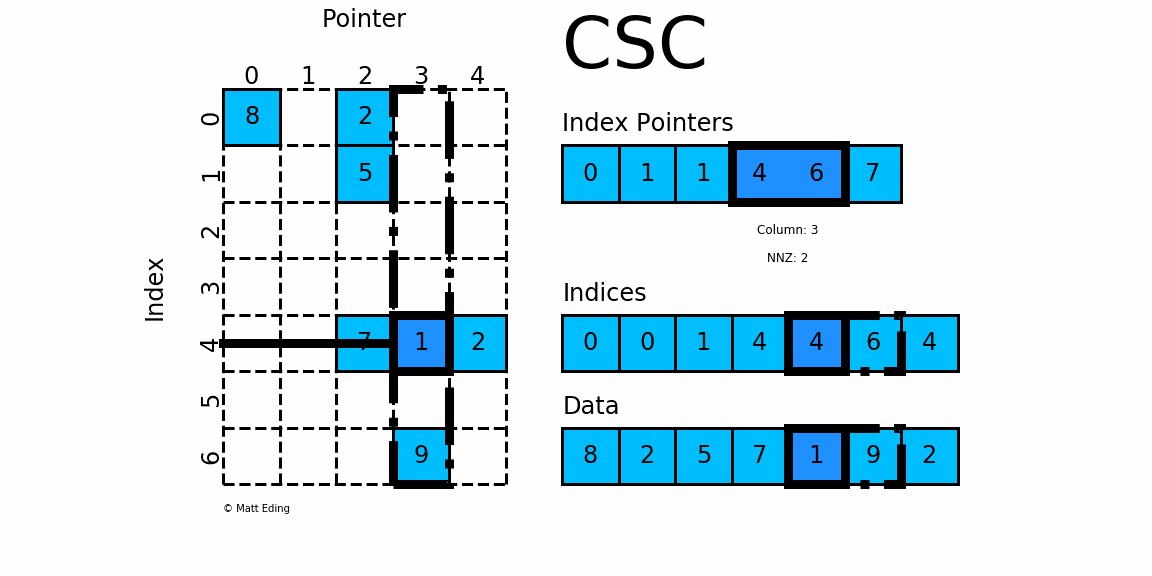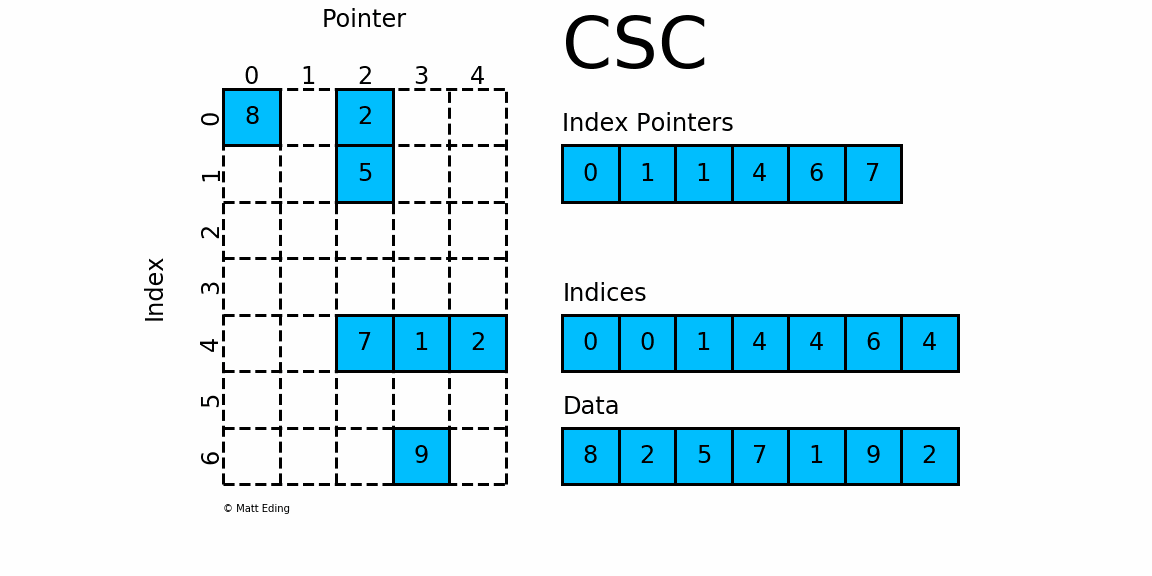
3.3 CSC - csc_matrix
3.3.1 Compressed Sparse Column Matrix 压缩稀疏列矩阵
-
csc_matrix是按列对矩阵进行压缩的
-
通过 indices, indptr,data 来确定矩阵,可以对比CSR
data表示矩阵中的非零数据- 对于第
i列而言,该行中非零元素的行索引为indices[indptr[i]:indptr[i+1]] - 可以将
indptr理解成利用其自身索引i来指向第i列元素的列索引 - 根据
[indptr[i]:indptr[i+1]],我就得到了该行中的非零元素个数,如:- 若
index[i] = 1且index[i+1] = 1,则第i列的没有非零元素 - 若
index[j] = 4且index[j+1] = 6,则第j列的非零元素的行索引为indices[4:6]
- 若
- 得到了列索引、行索引,相应的数据存放在:
data[indptr[i]:indptr[i+1]]
- 对于矩阵第0列,需要先得到其非零元素行索引
- 由
indptr[0] = 0和indptr[1] = 1可知,第0列行有1个非零元素。 - 它们的行索引为
indices[0:1] = [0],且存放的数据为data[0] = 8 - 因此矩阵第
0行的非零元素csc[0][0] = 8
- 由
- 对于矩阵第3列,同样需要先计算其非零元素行索引
- 由
indptr[3] = 4和indptr[4] = 6可知,第4行有2个非零元素。 - 它们的行索引为
indices[4:6] = [4, 6],且存放的数据为data[4] = 1,data[5] = 9 - 因此矩阵第
i行的非零元素csr[4][3] = 1,csr[6][3] = 9
- 由
3.3.2 适用场景
参考CSR
3.3.3 优缺点
对比参考CSR
3.3.4 实例化
csc_matrix(D):D代表密集矩阵;csc_matrix(S):S代表其他类型稀疏矩阵csc_matrix((M, N), [dtype]):构建一个shape为M*N的空矩阵,默认数据类型是d,csc_matrix((data, (row_ind, col_ind)), [shape=(M, N)]))- 三者关系:
a[row_ind[k], col_ind[k]] = data[k]
- 三者关系:
csc_matrix((data, indices, indptr), [shape=(M, N)])- 第i列的列索引存储在其中
indices[indptr[i]:indptr[i+1]] - 其对应值存储在中
data[indptr[i]:indptr[i+1]]
- 第i列的列索引存储在其中
3.3.5 特殊属性
data:稀疏矩阵存储的值,一维数组indices:存储矩阵有有非零值的行索引indptr:类似指向列索引的指针数组[has_sorted_indices]:索引indices是否排序
3.3.6 案例演示
# 生成数据
row = np.array([0, 2, 2, 0, 1, 2])
col = np.array([0, 0, 1, 2, 2, 2])
data = np.array([1, 2, 3, 4, 5, 6])# 创建矩阵
csc = sparse.csc_matrix((data, (row, col)), shape=(3, 3)).toarray()# 转为array
csc.toarray()
'''
array([[1, 0, 4],[0, 0, 5],[2, 3, 6]], dtype=int64)
'''# 按col列来压缩
# 对于第i列,非0数据行是indices[indptr[i]:indptr[i+1]] 数据是data[indptr[i]:indptr[i+1]]
# 在本例中
# 第0列,有非0的数据行是indices[indptr[0]:indptr[1]] = indices[0:2] = [0,2]
# 数据是data[indptr[0]:indptr[1]] = data[0:2] = [1,2],所以在第0列第0行是1,第2行是2
# 第1行,有非0的数据行是indices[indptr[1]:indptr[2]] = indices[2:3] = [2]
# 数据是data[indptr[1]:indptr[2] = data[2:3] = [3],所以在第1列第2行是3
# 第2行,有非0的数据行是indices[indptr[2]:indptr[3]] = indices[3:6] = [0,1,2]
# 数据是data[indptr[2]:indptr[3]] = data[3:6] = [4,5,6],所以在第2列第0行是4,第1行是5,第2行是6
3.4 BSR - bsr_matrix
3.4.1 Block Sparse Row Matrix 分块压缩稀疏行格式
- 基于行的块压缩,与csr类似,都是通过
data,indices,indptr来确定矩阵 - 与csr相比,只是data中的元数据由0维的数变为了一个矩阵(块),其余完全相同
- 块大小
blocksize- 块大小
(R, C)必须均匀划分矩阵(M, N)的形状。 - R和C必须满足关系:
M % R = 0和N % C = 0
- 块大小
3.4.2 适用场景
参考CSR
3.4.3 优缺点
优点:
- 与csr很类似
- 更适合于适用于具有密集子矩阵的稀疏矩阵
- 在某些情况下比csr和csc计算更高效。
3.4.4 实例化
bsr_matrix(D):D代表密集矩阵;bsr_matrix(S):S代表其他类型稀疏矩阵bsr_matrix((M, N), [blocksize =(R,C), [dtype]):构建一个shape为M*N的空矩阵,默认数据类型是d,(data, ij), [blocksize=(R,C), shape=(M, N)]- 两者关系:
a[ij[0,k], ij[1,k]] = data[k]]
- 两者关系:
bsr_matrix((data, indices, indptr), [shape=(M, N)])- 第i行的块索引存储在其中
indices[indptr[i]:indptr[i+1]] - 其相应块值存储在中
data[indptr[i]:indptr[i+1]]
- 第i行的块索引存储在其中
3.4.5 特殊属性
data:稀疏矩阵存储的值,一维数组indices:存储矩阵有有非零值的列索引indptr:类似指向列索引的指针数组blocksize:矩阵的块大小[has_sorted_indices]:索引indices是否排序
3.4.6 案例演示
# 生成数据
indptr = np.array([0,2,3,6])
indices = np.array([0,2,2,0,1,2])
data = np.array([1,2,3,4,5,6]).repeat(4).reshape(6,2,2)# 创建矩阵
bsr = bsr_matrix((data, indices, indptr), shape=(6,6)).todense()# 转为array
bsr.todense()
matrix([[1, 1, 0, 0, 2, 2],[1, 1, 0, 0, 2, 2],[0, 0, 0, 0, 3, 3],[0, 0, 0, 0, 3, 3],[4, 4, 5, 5, 6, 6],[4, 4, 5, 5, 6, 6]])
3.5 DOK- dok_matrix
3.5.1 Dictionary of Keys Matrix 按键字典矩阵
- 采用字典来记录矩阵中不为0的元素
- 字典的
key存的是记录元素的位置信息的元组,value是记录元素的具体值
3.5.2 适用场景
- 逐渐添加矩阵的元素
3.5.3 优缺点
优点:
- 对于递增的构建稀疏矩阵很高效,比如定义该矩阵后,想进行每行每列更新值,可用该矩阵。
- 可以高效访问单个元素,只需要O(1)
缺点:
- 不允许重复索引(coo中适用),但可以很高效的转换成coo后进行重复索引
3.5.4 实例化
dok_matrix(D):D代表密集矩阵;dok_matrix(S):S代表其他类型稀疏矩阵dok_matrix((M, N), [dtype]):构建一个shape为M*N的空矩阵,默认数据类型是d
3.5.5 案例演示
dok = sparse.dok_matrix((5, 5), dtype=np.float32)
for i in range(5):for j in range(5):dok[i,j] = i+j # 更新元素# zero elements are accessible
dok[(0, 0)] # = 0dok.keys()
# {(0, 0), ..., (4, 4)}dok.toarray()
'''
[[0. 1. 2. 3. 4.][1. 2. 3. 4. 5.][2. 3. 4. 5. 6.][3. 4. 5. 6. 7.][4. 5. 6. 7. 8.]]'''
3.6 LIL - lil_matrix
3.6.1 Linked List Matrix 链表矩阵
-
使用两个列表存储非0元素data
-
rows保存非零元素所在的列
-
可以使用列表赋值来添加元素,如
lil[(0, 0)] = 8
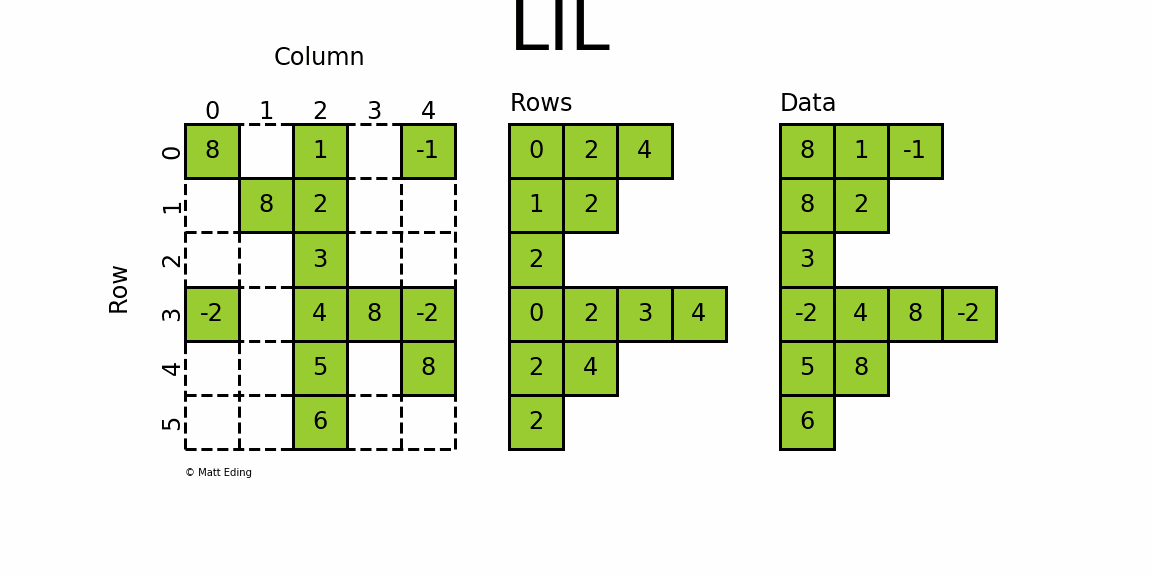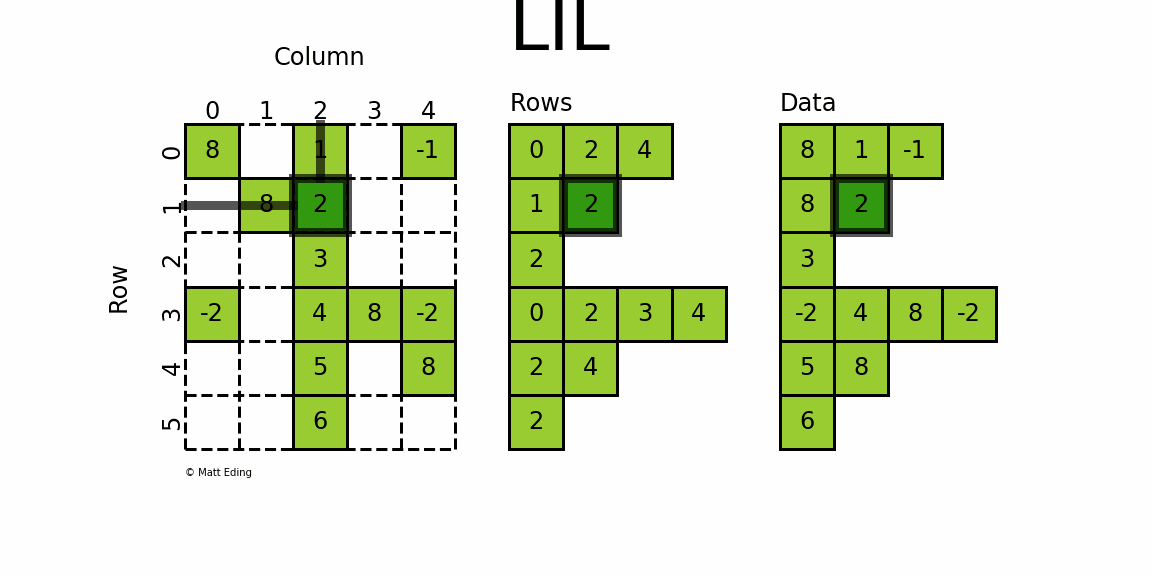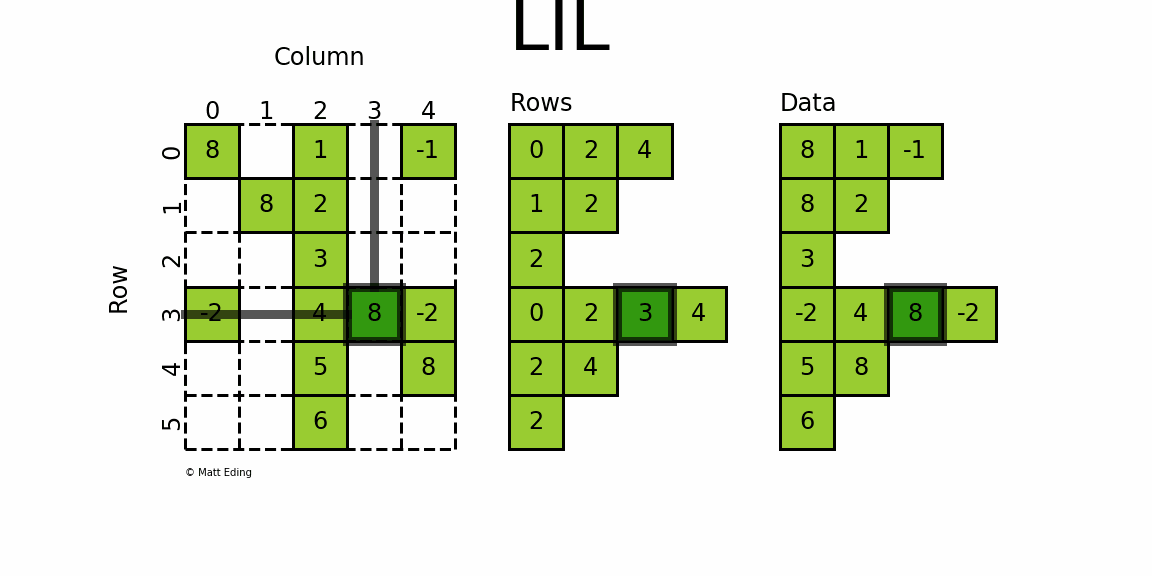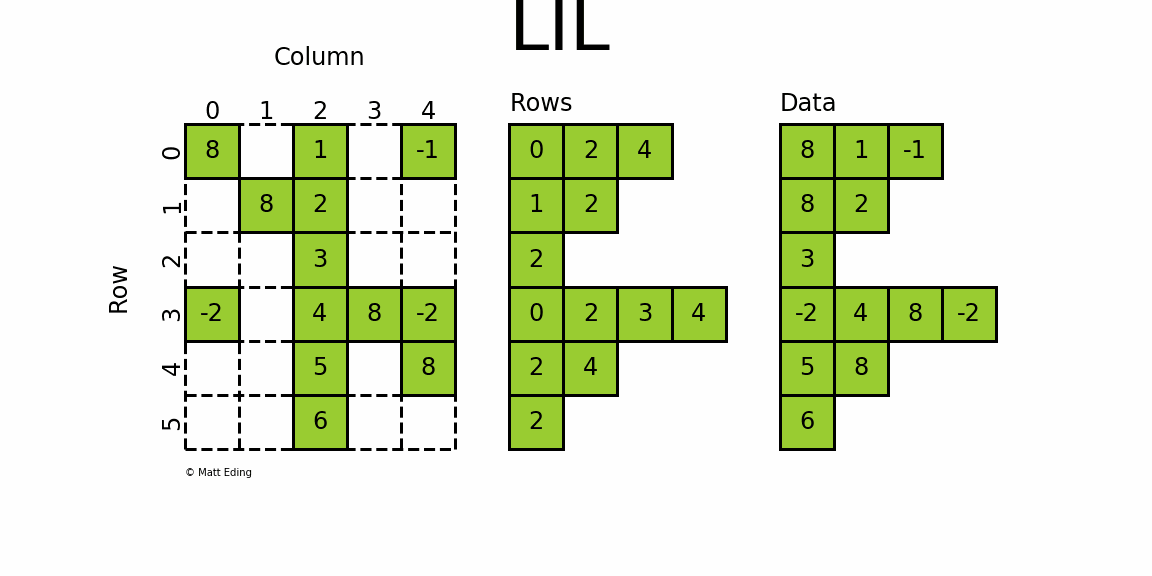
lil[(0, -1)] = 4:第0行的最后一列元素为4lil[(4, 2)] = 5:第4行第2列的元素为5
3.6.2 适用场景
- 适用的场景是逐渐添加矩阵的元素(且能快速获取行相关的数据)
- 需要注意的是,该方法插入一个元素最坏情况下可能导致线性时间的代价,所以要确保对每个元素的索引进行预排序
3.6.3 优缺点
优点:
- 适合递增的构建成矩阵
- 转换成其它存储方式很高效
- 支持灵活的切片
缺点:
- 当矩阵很大时,考虑用coo
- 算术操作,列切片,矩阵向量内积操作慢
3.6.4 实例化
lil_matrix(D):D代表密集矩阵;lil_matrix(S):S代表其他类型稀疏矩阵lil_matrix((M, N), [dtype]):构建一个shape为M*N的空矩阵,默认数据类型是d
3.6.5 特殊属性
data:存储矩阵中的非零数据rows:存储每个非零元素所在的列(行信息为列表中索引所表示)
3.6.6 案例演示
# 创建矩阵
lil = sparse.lil_matrix((6, 5), dtype=int)# 设置数值
# set individual point
lil[(0, -1)] = -1
# set two points
lil[3, (0, 4)] = [-2] * 2
# set main diagonal
lil.setdiag(8, k=0)# set entire column
lil[:, 2] = np.arange(lil.shape[0]).reshape(-1, 1) + 1# 转为array
lil.toarray()
'''
array([[ 8, 0, 1, 0, -1],[ 0, 8, 2, 0, 0],[ 0, 0, 3, 0, 0],[-2, 0, 4, 8, -2],[ 0, 0, 5, 0, 8],[ 0, 0, 6, 0, 0]])
'''# 查看数据
lil.data
'''
array([list([0, 2, 4]), list([1, 2]), list([2]), list([0, 2, 3, 4]),list([2, 4]), list([2])], dtype=object)
'''
lil.rows
'''
array([[list([8, 1, -1])],[list([8, 2])],[list([3])],[list([-2, 4, 8, -2])],[list([5, 8])],[list([6])]], dtype=object)
'''
3.7 DIA - dia_matrix
3.7.1 Diagonal Matrix 对角存储格式
-
dia_matrix通过两个数组确定:
data和offsetsdata:对角线元素的值offsets:第i个offsets是当前第i个对角线和主对角线的距离data[k:]存储了offsets[k]对应的对角线的全部元素
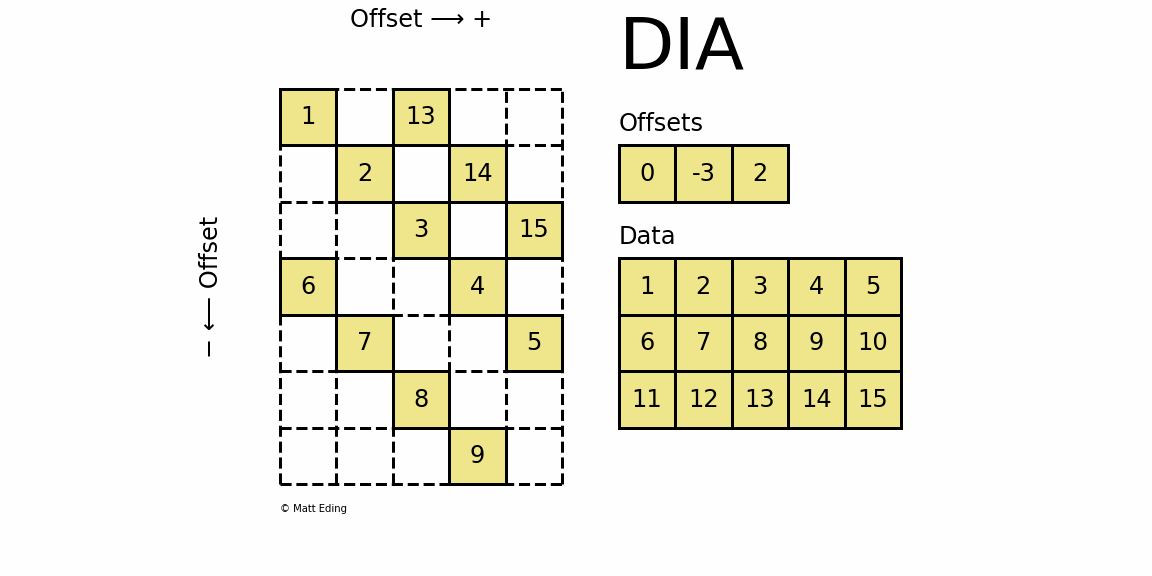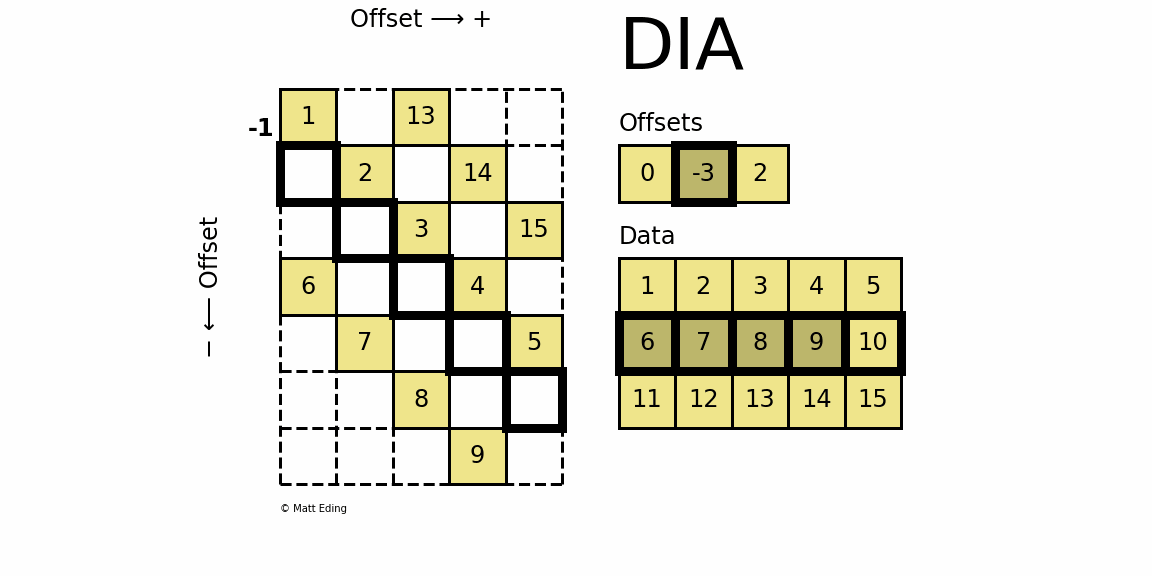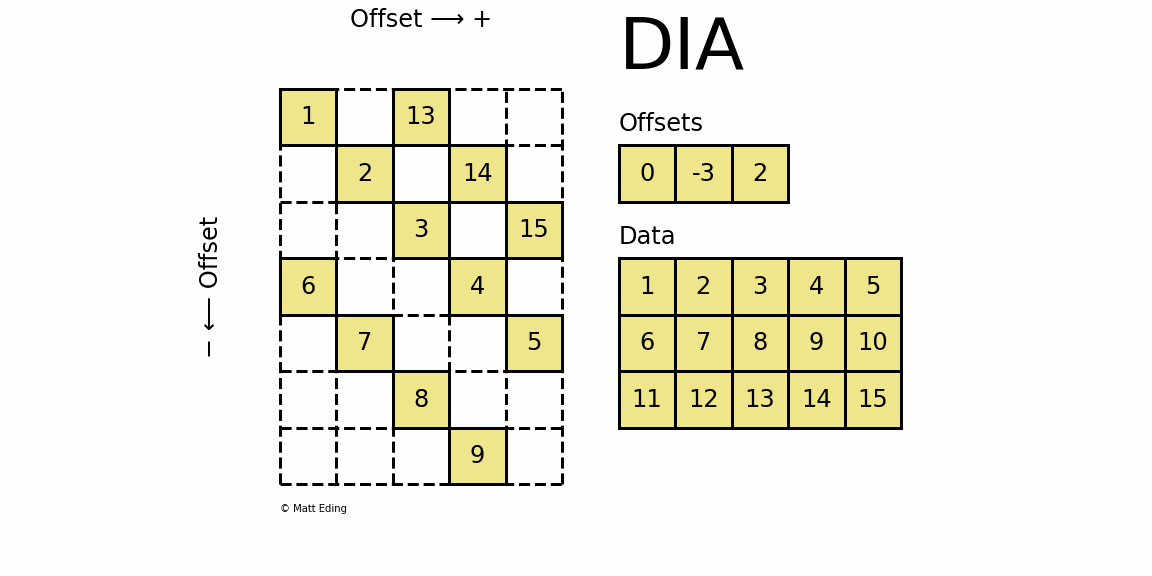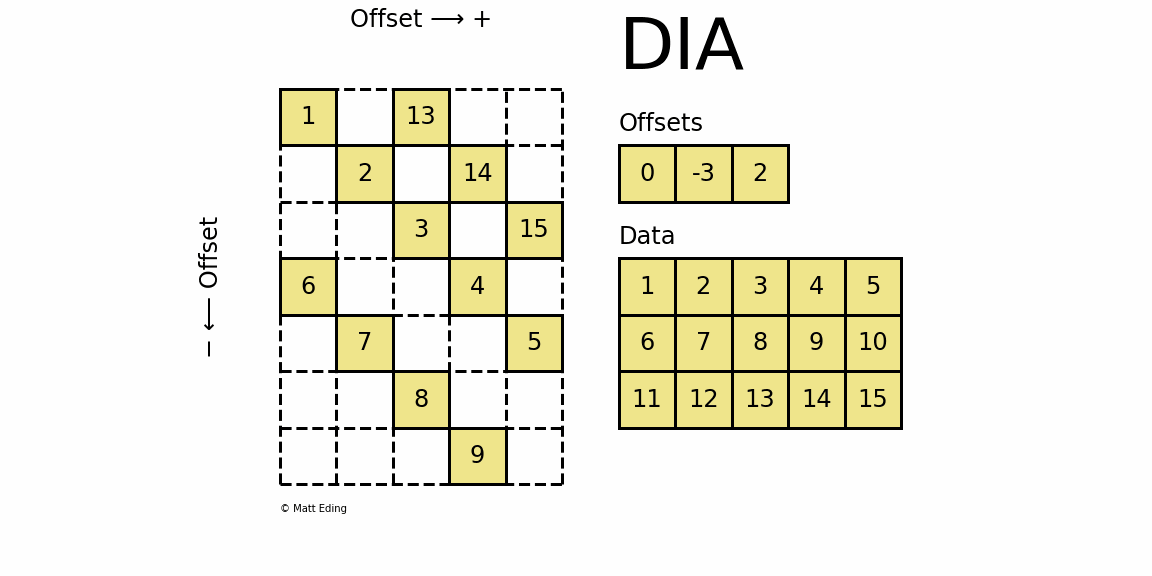
- 当
offsets[0] = 0时,表示该对角线即是主对角线,相应的值为[1, 2, 3, 4, 5] - 当
offsets[2] = 2时,表示该对角线为主对角线向上偏移2个单位,相应的值为[11, 12, 13, 14, 15]- 但该对角线上元素仅有三个 ,于是采用先出现的元素无效的原则
- 即前两个元素对构造矩阵无效,故该对角线上的元素为
[13, 14, 15]
3.7.2 适用场景
最适合对角矩阵的存储方式
3.7.3 实例化
dia_matrix(D):D代表密集矩阵;dia_matrix(S):S代表其他类型稀疏矩阵dia_matrix((M, N), [dtype]):构建一个shape为M*N的空矩阵,默认数据类型是d,dia_matrix((data, offsets)), [shape=(M, N)])):data[k,:]存储着对角偏移量为offset[k]的对角值
3.7.4 特殊属性
data:存储DIA对角值的数组offsets:存储DIA对角偏移量的数组
3.7.5 案例演示
# 生成数据
data = np.array([[1, 2, 3, 4], [5, 6, 0, 0], [0, 7, 8, 9]])
offsets = np.array([0, -2, 1])# 创建矩阵
dia = sparse.dia_matrix((data, offsets), shape=(4, 4))# 查看数据
dia.data
'''
array([[[1 2 3 4][5 6 0 0][0 7 8 9]])
'''# 转为array
dia.toarray()
'''
array([[1 7 0 0][0 2 8 0][5 0 3 9][0 6 0 4]])
'''
4.矩阵格式对比
| COO | DOK | LIL | CSR | CSC | BSR | DIA | Dense | |
|---|---|---|---|---|---|---|---|---|
| indexing | no | yes | yes | yes | yes | no† | no | yes |
| write-only | yes | yes | yes | no | no | no | no | yes |
| read-only | no | no | no | yes | yes | yes | yes | yes |
| low memory | yes | no | no | yes | yes | yes | yes | no |
| PyData sparse | yes | yes | no | no | no | no | no | n/a |
5.稀疏矩阵存取
5.1 存储 - save_npz
# 存储为npz文件
scipy.sparse.save_npz('sparse_matrix.npz', sparse_matrix)
5.2 读取 - load_npz
# 从npz文件中读取
mat = sparse.load_npz('./data/npz/test_x.npz')
5.3 存储大小比较
a = np.arange(100000).reshape(1000,100)
a[10: 300] = 0
b = sparse.csr_matrix(a)# 稀疏矩阵压缩存储到npz文件
sparse.save_npz('b_compressed.npz', b, True) # 文件大小:100KB# 稀疏矩阵不压缩存储到npz文件
sparse.save_npz('b_uncompressed.npz', b, False) # 文件大小:560KB# 存储到普通的npy文件
np.save('a.npy', a) # 文件大小:391KB# 存储到压缩的npz文件
np.savez_compressed('a_compressed.npz', a=a) # 文件大小:97KB• 1
对于存储到npz文件中的CSR格式的稀疏矩阵,内容为:
data.npy
format.npy
indices.npy
indptr.npy
shape.npy
本文仅作为个人学习记录使用, 不用于商业用途, 谢谢您的理解合作。
参考:
1.Sparse稀疏矩阵主要存储格式总结
相关文章:

稀疏矩阵(Sparse Matrix)
1.背景 在数据科学和深度学习等领域常会采用矩阵格式来存储数据,但当矩阵较为庞大且非零元素较少时, 如果依然使用dense的矩阵进行存储和计算将是极其低效且耗费资源的。所以,通常我们采用Sparse稀疏矩阵的方式来存储矩阵,提高存储…...

深度学习中的损失函数
文章目录一. Loss函数1. 均方差损失(Mean Squared Error Loss)2. 平均绝对误差损失(Mean Absolute Error Loss)3.(Huber Loss)4. 分位数损失(Quantile Loss)5. 交叉熵损失࿰…...

English Learning - L2 语音作业打卡 辅音咬舌音 [θ] [ð] Day29 2023.3.21 周二
English Learning - L2 语音作业打卡 辅音咬舌音 [θ] [] Day29 2023.3.21 周二💌发音小贴士:💌当日目标音发音规则/技巧:🍭 Part 1【热身练习】🍭 Part2【练习内容】🍭【练习感受】🍓元音 [θ]…...

【原始者-综述】
目录知识框架No.1 AcwingNo.2 LeetcodeNo.3 PTANo.4 蓝桥No.5 牛客网No.6 代码随想录知识框架 No.1 Acwing 那就点击这里转向自己的Acwing题解咯 单调栈,动态规划,贪心,回溯,二叉树,站与队列,双指针&#…...

C++内存模型
目录 一.内存分区 二,分区顺序 1 程序运行前 2 程序运行后 3.new操作符 一.内存分区 内存分区意义:不同区域存放的数据,赋予不同的生命周期, 给我们更大的灵活编程 内存可以分为以下几个区: 代码区:存放函数体的二进制代码…...
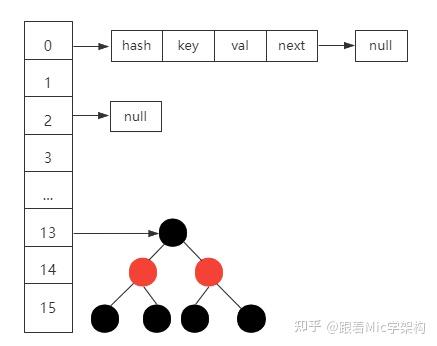
八股+面经
文章目录项目介绍Java基础MapHashMap v.s Hashtable(5点)ConcurrentHashMap v.s Hashtable(2点)代理模式1. 静态代理2. 动态代理2.1 JDK 动态代理机制2.2 CGLIB 动态代理机制Java并发线程volatilesynchronized线程池JVM类加载机制垃圾回收(GC)1. 引用类型…...
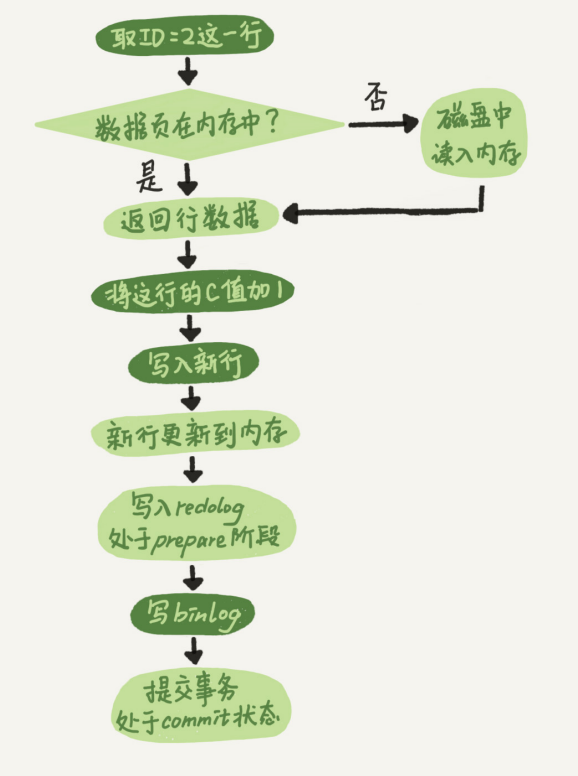
MySQL更新数据流程
1.mysql三种重要日志 redo log(重做日志):存在于引擎层,物理存储,通过设置innodb_flush_log_at_trx_xommit1 让其持久化到磁盘,保证引擎的crash-safe能力,遵从WAL技术(Write-Ahead …...
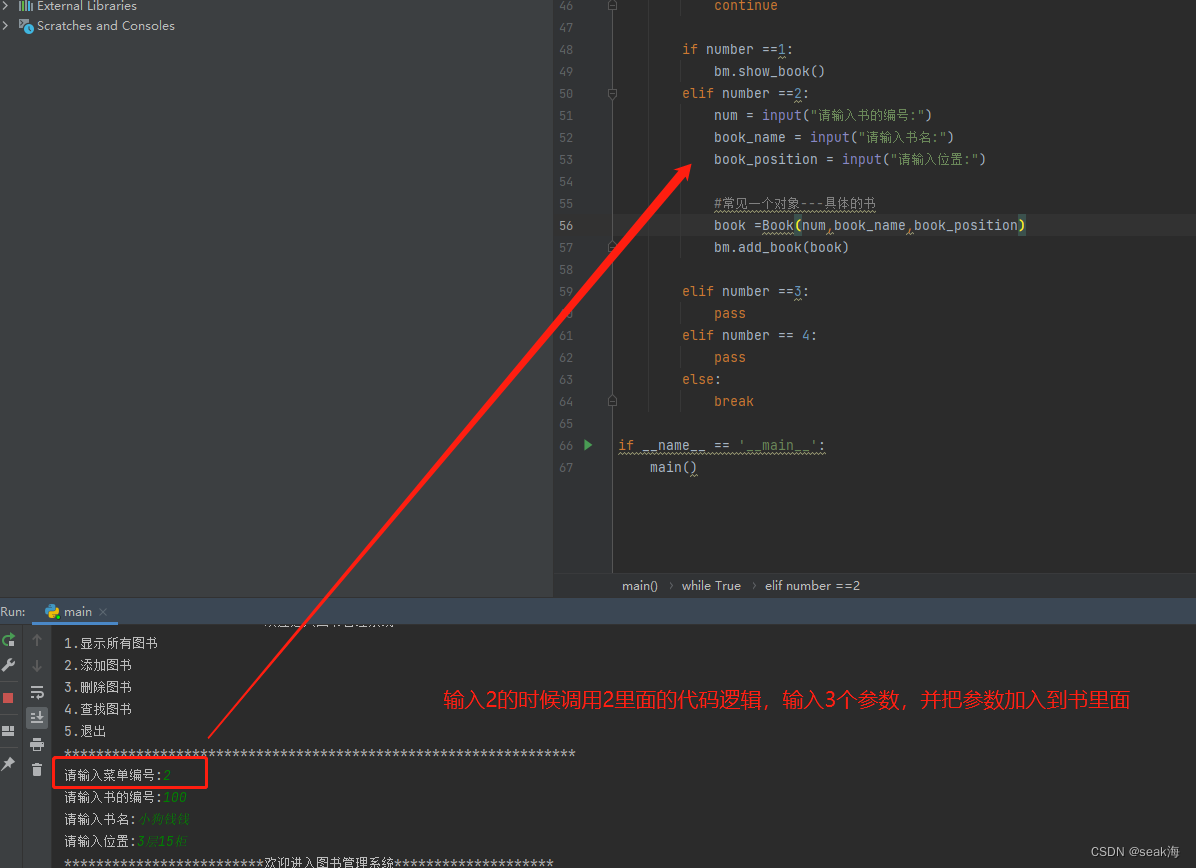
测试开发进阶系列课程
测试开发系列课程1.完善程序思维--------案列:图书管理系统的创建**(一)图书管理系统的创建**1.完善程序思维--------案列:图书管理系统的创建 (一)图书管理系统的创建 1.在main中写入主函数,…...
 对象树管理)
Qt源码阅读(三) 对象树管理
对象树管理 个人经验总结,如有错误或遗漏,欢迎各位大佬指正 😃 文章目录对象树管理设置父对象的作用设置父对象(setParent)完整源码片段分析对象的删除夹带私货时间设置父对象的作用 众所周知,Qt中,有为对象设置父对象…...
【Python入门第四十二天】Python丨NumPy 数组裁切
裁切数组 python 中裁切的意思是将元素从一个给定的索引带到另一个给定的索引。 我们像这样传递切片而不是索引:[start:end]。 我们还可以定义步长,如下所示:[start:end:step]。 如果我们不传递 start&…...
Anaconda配置Python新版本tensorflow库(CPU、GPU通用)的方法
本文介绍在Anaconda环境中,下载并配置Python中机器学习、深度学习常用的新版tensorflow库的方法。 在之前的两篇文章基于Python TensorFlow Estimator的深度学习回归与分类代码——DNNRegressor(https://blog.csdn.net/zhebushibiaoshifu/article/detail…...
加载模型时出现 OSError: Unable to load weights from pytorch checkpoint file 报错的解决
加载模型时出现 OSError: Unable to load weights from pytorch checkpoint file 报错的解决报错信息原因查明网传解决措施好消息我的解决措施报错信息 查了下,在网上还是个比较常见的报错 一般为加载某模型时突然报错 原因查明 一般为下载某个 XXX_model.bin 的…...

sessionStorage , localStorage 和cookie的区别
一.sessionStorage(临时存储)sessionStorage是HTML5中新增的Web Storage API之一,用于在浏览器中存储键值对数据,与localStorage类似,但是sessionStorage存储的数据在会话结束时会被清除。可以通过以下方式使用sessionStorage:存储…...

C# 实例详解委托之Func、Action、delegate
委托是.NET编程的精髓之一,在日常编程中经常用到,在C#中实现委托主要有Func、Action、delegate三种方式,这个文章主要就这三种委托的用法通过实例展开讲解。 【Func】:Func是带返回值的委托: 原型函数如下(以下展示的…...
如何选电脑
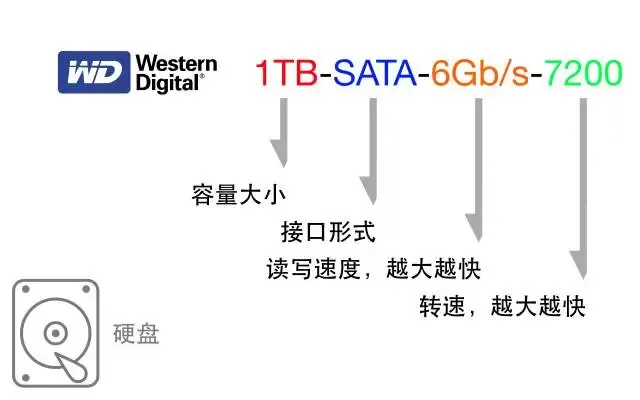
1、CPU(中央处理器) 怎么看CPU型号:CPU:系列-代数等级核心显卡型号电压后缀 例如CPU:i7-10750H : 1、系列:Intel的酷睿i3、i5、i7、i9这四个系列的CPU,数字越大就代表越高端。 2、代数:代表…...

SpringBoot项目创建
如果使用spring的源地址创建项目失败,就使用 阿里云的springBoot项目创建地址:https://start.aliyun.com/ 1.new 一个新的项目: 2.选择合适的版本java的JDK和maven项目 3.选择spring web依赖 4.直接finish 5. 删除无用的包,然后…...

神经衰弱该如何判断?确诊为神经衰弱,日常要做好这7大护理!
神经衰弱是由于长时间处于紧张或者压力的情况下导致精神出现兴奋或者疲乏现象而伴随着一系列症状。如情绪烦恼、容易激怒、睡眠障碍、肌肉出现紧张性疼痛等,生活中有很多人在自己的不到休息或者遇到强大打击时就会嘲笑自己患上神经衰弱。甚至一些会盲目采取措施&…...

Linux之进程替换
进程替换1.什么是进程替换2.替换函数2.1 execl函数2.2 execv函数2.3 execlp函数2.4 execvp函数2.5 在自己的C程序上如何运行其他语言的程序?2.6 execle 函数2.7 小结3.一个简易的shell1.什么是进程替换 fork()之后,父子各自执行父进程代码的一部分&…...

关于清除浮动
浮动最早是用来做图文排版,为了让块级元素同行显示,而html中块元素是有自己的排列规则,一般独占一行。所以有了浮动元素,一旦元素浮动了就会脱离文档流,产生问题。怎么去清除浮动:(1)…...

Uber H3 index 地图索引思考
H3 是 uber 设计的六边形空间索引,go 语言操作包是 h3-go,可以通过经纬度获取所在的 h3 六边形边界,每个经纬度对应的六边形都是确定的,每个六边形唯一对应了一个 h3index。在业务开发中,我们可以通过 h3index 来对地理…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
