当前位置： 首页 > news >正文

时间复杂度计算 递归（solve2 后续）

news 2026/2/8 21:47:59

原帖
最近校内比较忙，更新缓慢，致歉。
在这里插入图片描述
这里函数每次都需要遍历 h h h 和 m m m 之间的数（复杂度 O ( n ) O(n) O(n)），所以和 solve1 略有不同。仍然假设 T ⁡ ( n ) \operatorname{T}(n) T(n) 表示 m − h + 1 = n m-h+1=n m−h+1=n 时的复杂度。
T ⁡ ( n ) = 2 × T ⁡ ( n / 2 ) + n = 2 × ( 2 × T ⁡ ( n / 4 ) + n / 2 ) + n = 4 × T ⁡ ( n / 4 ) + 2 n \operatorname{T}(n)=2\times\operatorname{T}(n/2)+n=2\times(2\times\operatorname{T}(n/4)+n/2)+n=4\times\operatorname{T}(n/4)+2n T(n)=2×T(n/2)+n=2×(2×T(n/4)+n/2)+n=4×T(n/4)+2n
总结一下规律，就是： T ⁡ ( n ) = 2 k × T ⁡ ( n / 2 k ) + k n \operatorname{T}(n)=2^k\times\operatorname{T}(n/2^k)+kn T(n)=2k×T(n/2k)+kn，这里 k = l o g 2 n k=log_2n k=log2​n。（假设 k k k 是下取整的，造成的误差在计算时间复杂度时可忽略不计）。
T ⁡ ( n ) = 2 k + n k = n + n k \operatorname{T}(n)=2^{k}+nk=n+nk T(n)=2k+nk=n+nk，相当于 O ( n l o g n ) O(nlogn) O(nlogn) 的复杂度。

相关文章：

时间复杂度计算 递归（solve2 后续）

原帖 最近校内比较忙，更新缓慢，致歉。 这里函数每次都需要遍历 h h h 和 m m m 之间的数（复杂度 O ( n ) O(n) O(n)），所以和 solve1 略有不同。仍然假设 T ⁡ ( n ) \operatorname{T}(n) T(n) 表示 m − h 1 n…...

编程日记 2024/9/18 6:06:19

Nginx：高性能Web服务器与反向代理的深度剖析

Nginx：高性能Web服务器与反向代理的深度剖析 Nginx（发音为“engine X”）是一款轻量级但功能强大的Web服务器和反向代理服务器，以其高并发处理能力、低内存占用和灵活的扩展性在互联网项目中得到了广泛应用。本文将深入探讨Nginx…...

编程日记 2024/9/18 6:05:18

JavaSE - 面向对象编程03

01 多态 01_01 认识多态 01_02 多态的好处和缺点 【1】好处：① 可以解耦合，扩展性更强，父类引用指向的子类对象可以随时切换，而后面的逻辑代码并不需要更改。 ② 使用父类引用可以作为方法的形参或返回类型来接收一切子类对象。…...

编程日记 2024/9/18 6:03:15

变电站缺陷数据集8307张，带xml标注和txt标注，可以直接用于yolo训练

变电站缺陷数据集8307张， 带xml标注和txt标注，可以直接用于yolo训练，赠附五个脚本 变电站缺陷数据集 数据集概述 变电站缺陷数据集是一个专门针对变电站设备和环境缺陷检测的图像数据集。该数据集包含了8307张经过标注的图像，旨…...

编程日记 2024/9/18 5:58:00

Redis的存储原理和数据模型

一、Redis是单线程还是多线程呢？ 我们通过跑redis的代码，查看运行的程序可以得知，Redis本身其实是个多线程，其中包括redis-server，bio_close_file，bio_aof_fsync，bio_lazy_free，io_t…...

编程日记 2024/9/18 5:56:59

Linux 文件与目录操作命令详解

文章目录 前言创建文件1. touch2. vim 文件内容显示3. cat4. more5. less6. head7. tail 文件（目录）复制、删除和移动8. cp9. rm10. mv 压缩文件与解压缩11. gzip12. zip 和 unzip 创建目录13. mkdir 删除目录14. rmdir 改变工作目录15. cd16. pwd 显示目…...

编程日记 2024/9/18 5:52:56

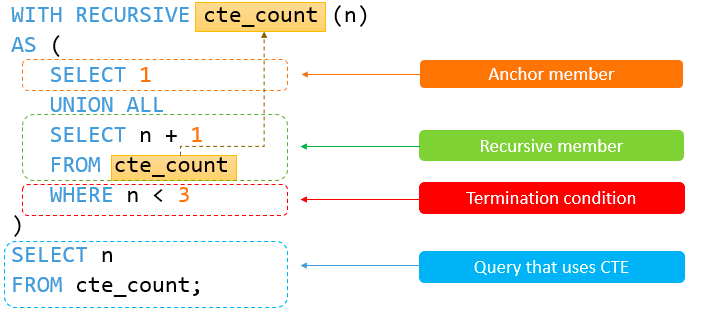
MySQL篇（窗口函数/公用表达式（CTE））

目录 讲解一：窗口函数 一、简介 二、常见操作 1. sumgroup by常规的聚合函数操作 2. sum窗口函数的聚合操作 三、基本语法 1. Function(arg1,..., argn) 1.1. 聚合函数 sum函数：求和 min函数 ：最小值 1.2. 排序函数 1.3. 跨行函数…...

编程日记 2024/9/18 5:51:54

408算法题leetcode--第七天

283. 移动零 283. 移动零思路&#xff1a;代码中注释阐述时间&#xff1a;O(n)&#xff1b;空间&#xff1a;O(1) class Solution { public:void moveZeroes(vector<int>& nums) {// 简单思路&#xff1a;用一个辅助数组&#xff0c;将非0元素复制到里面// 双指针&…...

编程日记 2024/9/18 5:49:52

政务安全体系构建中的挑战

在数字化政务安全体系的构建过程中&#xff0c;面临着几个关键的挑战&#xff1a; ▋挑战一&#xff1a;安全防护滞后现代网络攻击技术不断演进&#xff0c;攻击手段日益多样化&#xff0c;如高级持续性威胁&#xff08;APT&#xff09;和勒索软件等新型攻击方式频繁出现。这些…...

编程日记 2024/9/18 5:48:51

基于EchoMimic加速版，可编辑标志点控制实现逼真音频驱动的肖像动画

EchoMimic 是蚂蚁集团终端技术部门开发的一项技术，旨在通过音频驱动生成逼真的肖像动画。对于那些初次接触这项技术的用户，本教程将带你逐步了解如何设置开发环境、获取项目代码、安装依赖，并最终成功运行示例生成自己的肖像动画。 文章目录 项目代码安装依赖业务拓展参数调…...

编程日记 2024/9/18 5:45:48

【STM32 HAL库】IIC通信与CubeMX配置

【STM32 HAL库】IIC通信与CubeMX配置 前言理论IIC总线时序图IIC写数据IIC读数据 轮询模式CubeMX配置应用示例AHT20初始化初始化函数读取说明读取函数 中断模式CubeMX配置状态机图fsm.caht20.c DMA模式CubeMX配置代码 前言 本文为笔者学习 IIC 通信的总结&#xff0c;基于keysk…...

编程日记 2024/9/18 5:41:44

iPhone 上丢失了重要的联系人？如何恢复已删除的 iPhone 联系人

丢失 iPhone 上的联系人可能会带来灾难。无论是一份很棒的新工作机会、潜在的恋爱对象&#xff0c;还是您一直想打电话的老朋友&#xff0c;如果您打开“联系人”应用时看到空白&#xff0c;这绝不是好事。不过&#xff0c;一切并非全无&#xff0c;仍然可以通过备份或专业软件…...

编程日记 2024/9/18 5:40:42

【有啥问啥】弱监督学习新突破：格灵深瞳多标签聚类辨别（Multi-Label Clustering and Discrimination, MLCD）方法

弱监督学习新突破&#xff1a;格灵深瞳多标签聚类辨别&#xff08;Multi-Label Clustering and Discrimination, MLCD&#xff09;方法 引言 在视觉大模型领域&#xff0c;如何有效利用海量无标签图像数据是一个亟待解决的问题。传统的深度学习模型依赖大量人工标注数据&…...

编程日记 2024/9/18 5:39:41

[强化你的LangChain工具创建技能：从基础到进阶]

强化你的LangChain工具创建技能&#xff1a;从基础到进阶 在现代AI开发中&#xff0c;为语言模型和智能代理提供工具是提升其功能的关键一步。本指南将带你深入了解如何在LangChain中创建工具&#xff0c;从简单的函数到复杂的可配置工具。 引言 在构建智能代理时&#xff0…...

编程日记 2024/9/18 5:38:40

4.提升客户服务体验：ChatGPT在客服中的应用（4/10）

本文大纲旨在指导撰写一篇全面探讨ChatGPT如何通过优化客户服务流程、提供实际应用案例和用户反馈&#xff0c;以提升客户服务体验的深入博客文章。 引言 在当今竞争激烈的商业环境中&#xff0c;客户服务已成为企业成功的关键因素。优质的客户服务不仅能够增强客户满意度和忠…...

编程日记 2024/9/18 5:37:39

Gradio导入AIGC大模型创建web端智能体聊天机器人，python（2）

Gradio导入AIGC大模型创建web端智能体聊天机器人&#xff0c;python&#xff08;2&#xff09; 选用这个大模型&#xff1a; https://huggingface.co/HuggingFaceTB/SmolLM-1.7B-Instructhttps://huggingface.co/HuggingFaceTB/SmolLM-1.7B-Instruct原因是该模型相对比较小&am…...

编程日记 2024/9/18 5:36:38

PEM 格式

文章目录 1.简介2.格式和内容3.常见用途4.标准化5.示例参考文献 1.简介 .pem 文件扩展名代表“Privacy Enhanced Mail”&#xff0c;但它被用于比电子邮件更广泛的上下文中&#xff0c;主要关联于加密、SSL/TLS 和证书管理。PEM 格式是一种用于存储和发送加密信息的标准&#…...

编程日记 2024/9/18 5:34:36

Android前台服务如何在后台启动activity？

本来最近在开发一个app保活另外一个app的功能&#xff0c;方案介绍如下&#xff1a; 应用A 启动一个前台服务保活自己应用A 用grpc连接应用B(服务端)是否存活如果发现B不存活&#xff0c;则在服务中拉起B 这次没有做好调研&#xff0c;直接开始了开发工作&#xff0c;等grpc都…...

编程日记 2024/9/18 5:33:35

c#visionpro开发 方法统计

toolblock开发 vpp第二种简单加载方式 public Cognex.VisionPro.ToolBlock.CogToolBlock ToolBlock1;//初始化后实例化一个方法 //窗口运行程序内部 ToolBlock1 (CogToolBlock)CogSerializer.LoadObjectFromFile(“tjjc.vpp”); MessageBox.Show(“算法加载成功”);//复制一个…...

编程日记 2024/9/18 5:32:34

dedecms——四种webshell姿势

姿势一&#xff1a;通过文件管理器上传WebShell 步骤一&#xff1a;访问目标靶场其思路为 dedecms 后台可以直接上传任意文件&#xff0c;可以通过文件管理器上传php文件获取webshell 步骤二&#xff1a;登陆到后台点击【核心】--》 【文件式管理器】--》 【文件上传】将准备好…...

编程日记 2024/9/18 5:31:33

MySQL 隔离级别：脏读、幻读及不可重复读的原理与示例

一、MySQL 隔离级别 MySQL 提供了四种隔离级别，用于控制事务之间的并发访问以及数据的可见性，不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式，具体如下： 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交（READ UNCOMMITTED）允许出现允许…...

编程新知 2025/9/16 21:01:58

YSYX学习记录（八）

C语言&#xff0c;练习0&#xff1a; 先创建一个文件夹&#xff0c;我用的是物理机&#xff1a; 安装build-essential 练习1&#xff1a; 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件&#xff0c;随机修改或删除一部分&#xff0c;之后…...

编程新知 2026/1/24 14:31:01

在四层代理中还原真实客户端ngx_stream_realip_module

一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡&#xff08;如 HAProxy、AWS NLB、阿里 SLB&#xff09;发起上游连接时&#xff0c;将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后&#xff0c;ngx_stream_realip_module 从中提取原始信息…...

编程新知 2026/1/4 5:02:00

Robots.txt 文件

什么是robots.txt&#xff1f; robots.txt 是一个位于网站根目录下的文本文件&#xff08;如&#xff1a;https://example.com/robots.txt&#xff09;&#xff0c;它用于指导网络爬虫&#xff08;如搜索引擎的蜘蛛程序&#xff09;如何抓取该网站的内容。这个文件遵循 Robots…...

编程新知 2025/9/9 5:38:23

ElasticSearch搜索引擎之倒排索引及其底层算法

文章目录 一、搜索引擎1、什么是搜索引擎？2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长，文件大。2.其次，树深，IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

编程新知 2026/1/30 17:10:19

Android15默认授权浮窗权限

我们经常有那种需求&#xff0c;客户需要定制的apk集成在ROM中&#xff0c;并且默认授予其【显示在其他应用的上层】权限&#xff0c;也就是我们常说的浮窗权限&#xff0c;那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

编程新知 2026/2/1 4:13:59

C# 求圆面积的程序（Program to find area of a circle）

给定半径r&#xff0c;求圆的面积。圆的面积应精确到小数点后5位。 例子&#xff1a; 输入&#xff1a;r 5 输出&#xff1a;78.53982 解释&#xff1a;由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982&#xff0c;因为我们只保留小数点后 5 位数字。 输…...

编程新知 2026/2/8 9:34:11

AI，如何重构理解、匹配与决策？

AI 时代&#xff0c;我们如何理解消费&#xff1f; 作者&#xff5c;王彬 封面&#xff5c;Unplash 人们通过信息理解世界。 曾几何时&#xff0c;PC 与移动互联网重塑了人们的购物路径&#xff1a;信息变得唾手可得&#xff0c;商品决策变得高度依赖内容。 但 AI 时代的来…...

编程新知 2026/1/30 2:33:11

【JVM】Java虚拟机（二）——垃圾回收

目录 一、如何判断对象可以回收 &#xff08;一&#xff09;引用计数法 &#xff08;二&#xff09;可达性分析算法 二、垃圾回收算法 &#xff08;一&#xff09;标记清除 &#xff08;二&#xff09;标记整理 &#xff08;三&#xff09;复制 &#xff08;四&#xff…...

编程新知 2026/1/31 9:49:23

Spring AI Chat Memory 实战指南：Local 与 JDBC 存储集成

一个面向 Java 开发者的 Sring-Ai 示例工程项目&#xff0c;该项目是一个 Spring AI 快速入门的样例工程项目&#xff0c;旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计&#xff0c;每个模块都专注于特定的功能领域&#xff0c;便于学习和…...

编程新知 2025/10/16 14:46:22