线性DP——AcWing 898. 数字三角形、AcWing 895. 最长上升子序列
AcWing 898. 数字三角形
1.题目
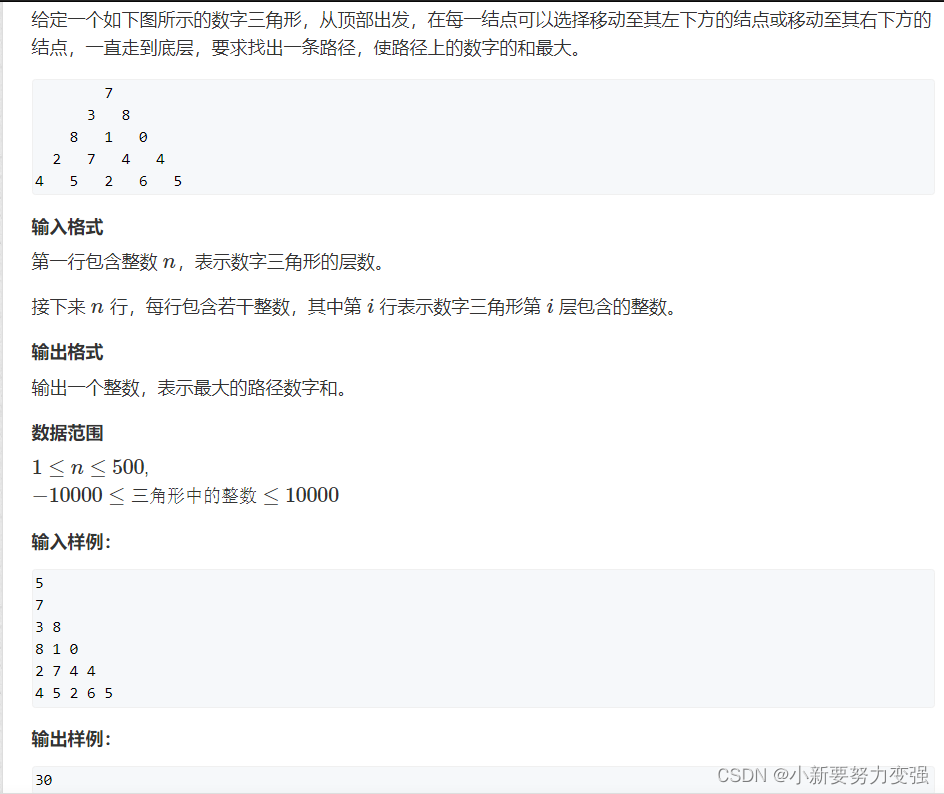
898. 数字三角形
2.思路
DP问题首先考虑状态转移方程,定义一个集合f ( i , j) ,表示从第一个数字(1,1)走到第 i行,第 j列(i , j)的所有方案的集合,那么我们要求的就是其中方案的整数之和的最大值。
这个点可以由左上方(i−1 , j)走过来,即f( i-1, j)+a(i , j)
这个点也可以由右上方(i−1,j−1)走过来,即f( i-1, j-1)+a(i , j)
所以状态转移方程就是f(i , j)=max{ f( i-1, j) , f( i-1, j-1) } + a(i , j)
这个思路是从上往下算,当向下走的时候,需要考虑边界问题。也就是对于f[2][1]的时候,f[1]f[0]并没有设置这个值,默认为0,题中的数字有负数,则会出现错误的最大值。需要对于f进行重置,置为Integer.MIN_VALUE,同样也可以从下往上算
3.Ac代码
思路一
import java.util.Arrays;
import java.util.Scanner;public class Main {static int N=510;static int [][]a=new int[N][N]; //存储每一层数字static int [][]f=new int[N][N]; //从第一个数字走到第 i行,第 j列元素的方案集合public static void main(String[] args) {Scanner sc=new Scanner(System.in);int n=sc.nextInt();for (int i = 1; i <=n; i++) {for (int j = 1; j <=i; j++) {a[i][j]=sc.nextInt();}}//因为可能这个数的上面左右两边都没有数,添加一个默认值for (int i = 0; i <=n; i++) {for (int j = 0; j <=i+1; j++) {f[i][j]=Integer.MIN_VALUE;}}//第一个方案只有这一种情况f[1][1]=a[1][1];for (int i=2; i<=n; i++){for(int j=1;j<=i;j++){f[i][j]=Math.max(f[i-1][j-1],f[i-1][j]) + a[i][j];}}int res=Integer.MIN_VALUE;for(int i=1;i<=n;i++){res=Math.max(res,f[n][i]);}System.out.println(res);}
}
思路二
import java.util.Arrays;
import java.util.Scanner;public class Main {static int N=510;static int [][]a=new int[N][N]; //存储每一层数字static int [][]f=new int[N][N]; //从第一个数字走到第 i行,第 j列元素的方案集合public static void main(String[] args) {Scanner sc=new Scanner(System.in);int n=sc.nextInt();for (int i = 1; i <=n; i++) {for (int j = 1; j <=i; j++) {a[i][j]=sc.nextInt();}}for (int i = n; i >= 1; i--) {//从最后一排开始走,从下往上。for (int j = 1; j <= i; j++) {f[i][j] = Math.max(f[i + 1][j + 1], f[i + 1][j]) + a[i][j];}}System.out.println(f[1][1]);}
}
AcWing 895. 最长上升子序列
1.题目
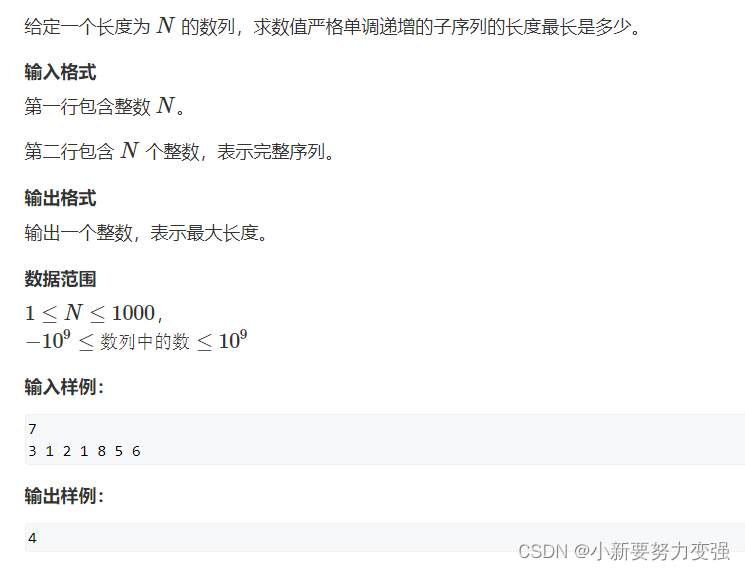
895. 最长上升子序列
2.思路
首先还是考虑状态表示,定义一个fi 表示从第一个数开始算,以第 i个数结尾的最长上升子序列,如果我们选第1个数,那么对应的就是f1
如果我们选第2个数,那么对应的就是f2
如果我们选第j个数,那么对应的就是f j
所以状态转移方程就是f i=max (f i +1)
3.Ac代码
import java.util.Scanner;public class Main {static int N=1010;static int []a=new int[N]; //存储数组static int []f=new int[N]; //fi 表示从第一个数开始算,以第 i个数结尾的最长上升子序列public static void main(String[] args) {Scanner sc=new Scanner(System.in);int n=sc.nextInt();for (int i = 1; i <=n; i++) {a[i]=sc.nextInt();}int res=0;for (int i = 1; i <=n; i++) {f[i]=1;for (int j = 1; j < i; j++) {if(a[j]<a[i]){f[i]=Math.max(f[i],f[j]+1);}}res=Math.max(res,f[i]);}System.out.println(res);}
}
感谢你能看完,如果对你有帮助的话,点个赞支持下
相关文章:

线性DP——AcWing 898. 数字三角形、AcWing 895. 最长上升子序列
AcWing 898. 数字三角形 1.题目 898. 数字三角形 2.思路 DP问题首先考虑状态转移方程,定义一个集合f ( i , j) ,表示从第一个数字(1,1)走到第 i行,第 j列(i , j)的所有方案的集合,…...
SpringMVC
SpringMVC配置 引入Maven依赖 (springmvc)web.xml配置DispatcherServlet配置 applicationContext 的 MVC 标记开发Controller控制器 几点注意事项: 在web.xml中 配置<load-on-startup> 0 </load-on-startup> 会自动创建Spring…...
)
C++模板基础(二)
函数模板(二) ● 模板实参的类型推导 – 如果函数模板在实例化时没有显式指定模板实参,那么系统会尝试进行推导 template<typename T> void fun(T input, T input2) {std::cout << input << \t << input2 << …...
什么是linux内核态、用户态?
目录标题为什么需要区分内核空间与用户空间内核态与用户态如何从用户空间进入内核空间整体结构为什么需要区分内核空间与用户空间 在 CPU 的所有指令中,有些指令是非常危险的,如果错用,将导致系统崩溃,比如清内存、设置时钟等。如…...

day8—选择题
文章目录1.Test.main() 函数执行后的输出是(D)2. JUnit主要用来完成什么(D)3.下列选项中关于Java中super关键字的说法正确的是(A)1.Test.main() 函数执行后的输出是(D) public clas…...
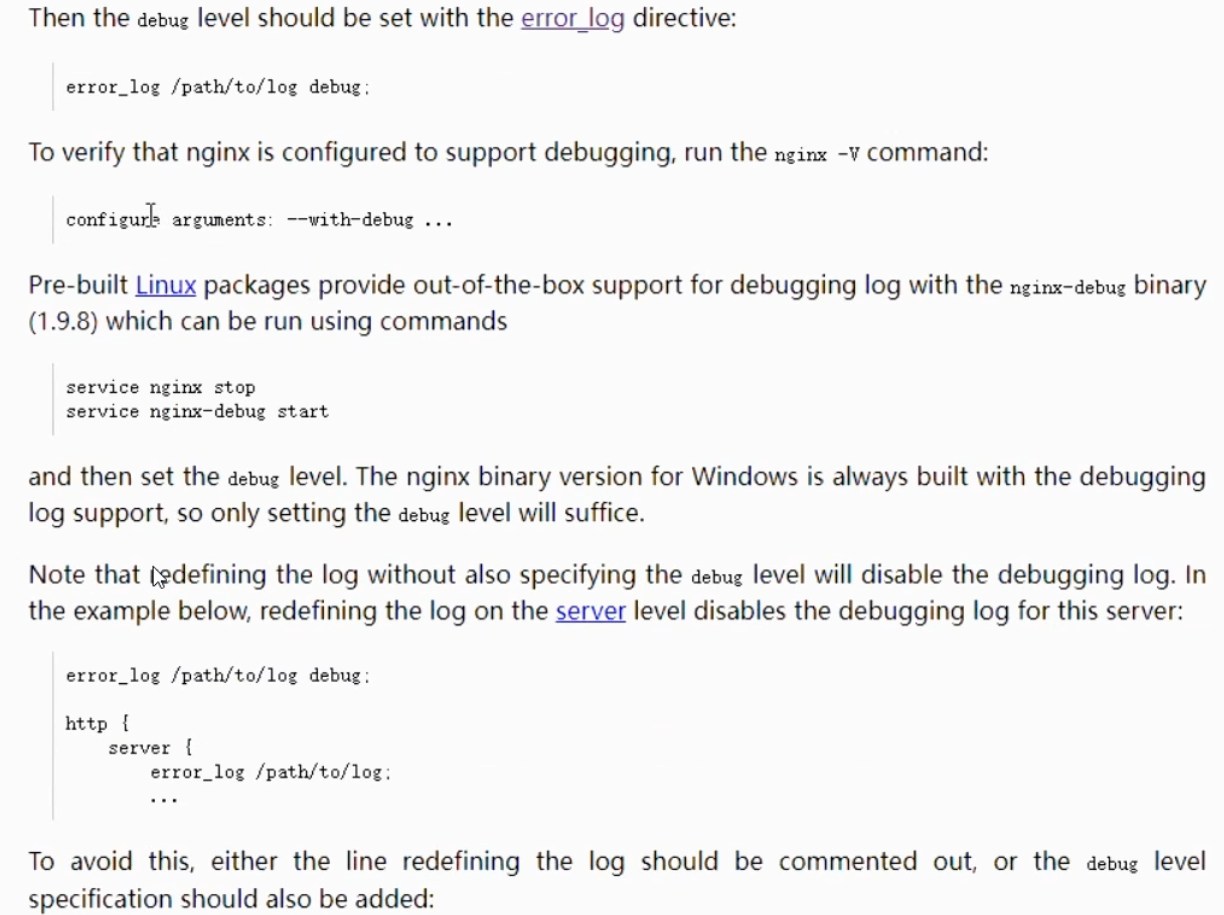
ngx错误日志error_log配置
ngx之error_log 日志配置格式: 常见的错误日志级别 错误日志可配置位置 关闭error_log配置 设置debug 日志级别的前提: ngx之error_log 日志配置格式: error_log 存放路径 日志级别 例: error_log /usr/local/log…...

1.11、自动化
自动化 一、java 手机自动化 首先new DesertCapabilities(这是一个类) setCapability – 设置信息 获取appium的驱动对象 new AppiumDriver – 本机IP地址:端口号/wd/hub,前面的设置值信息 driver.findElementById() – 通过id找位置 click() – 点击 &…...
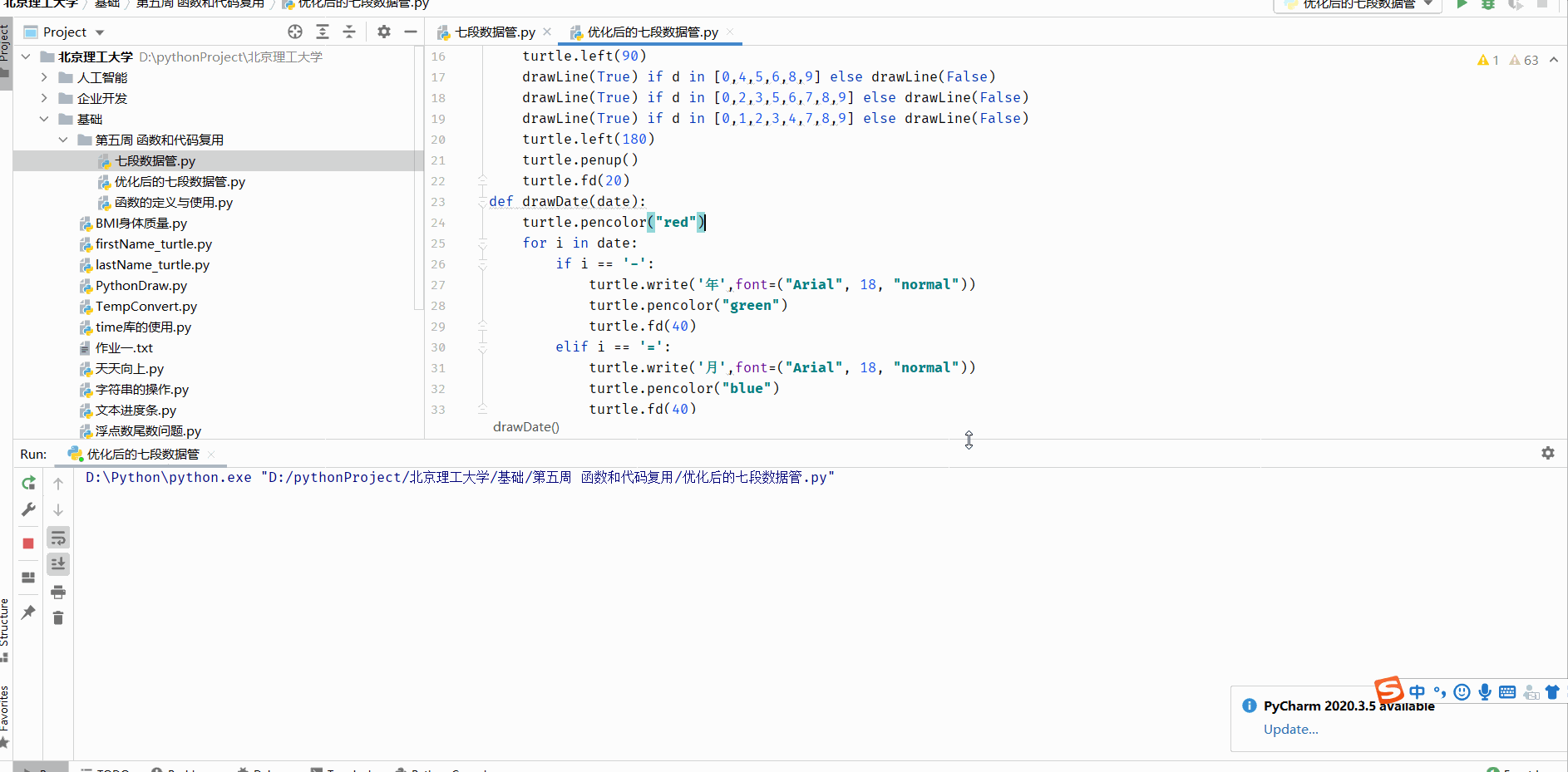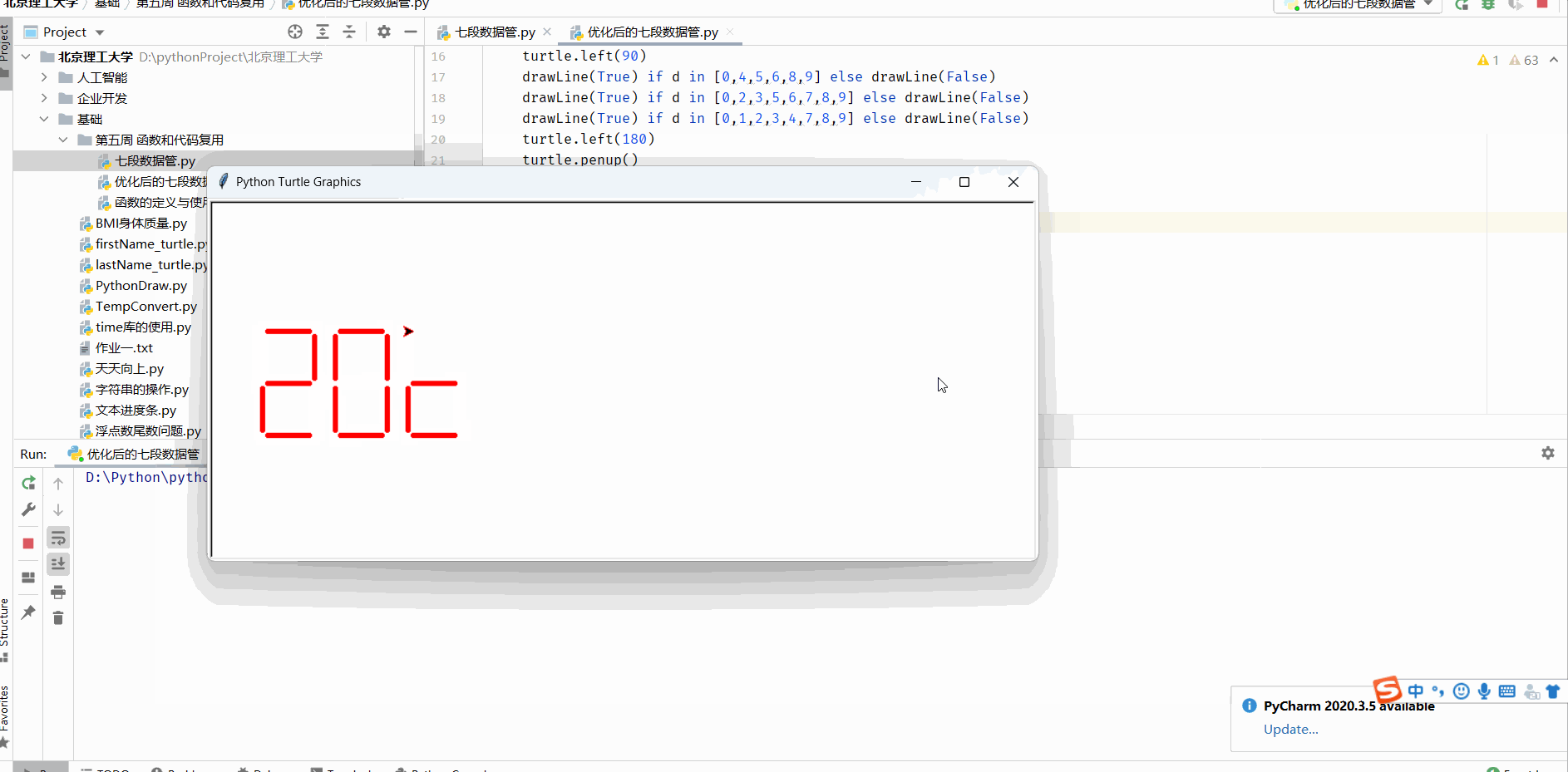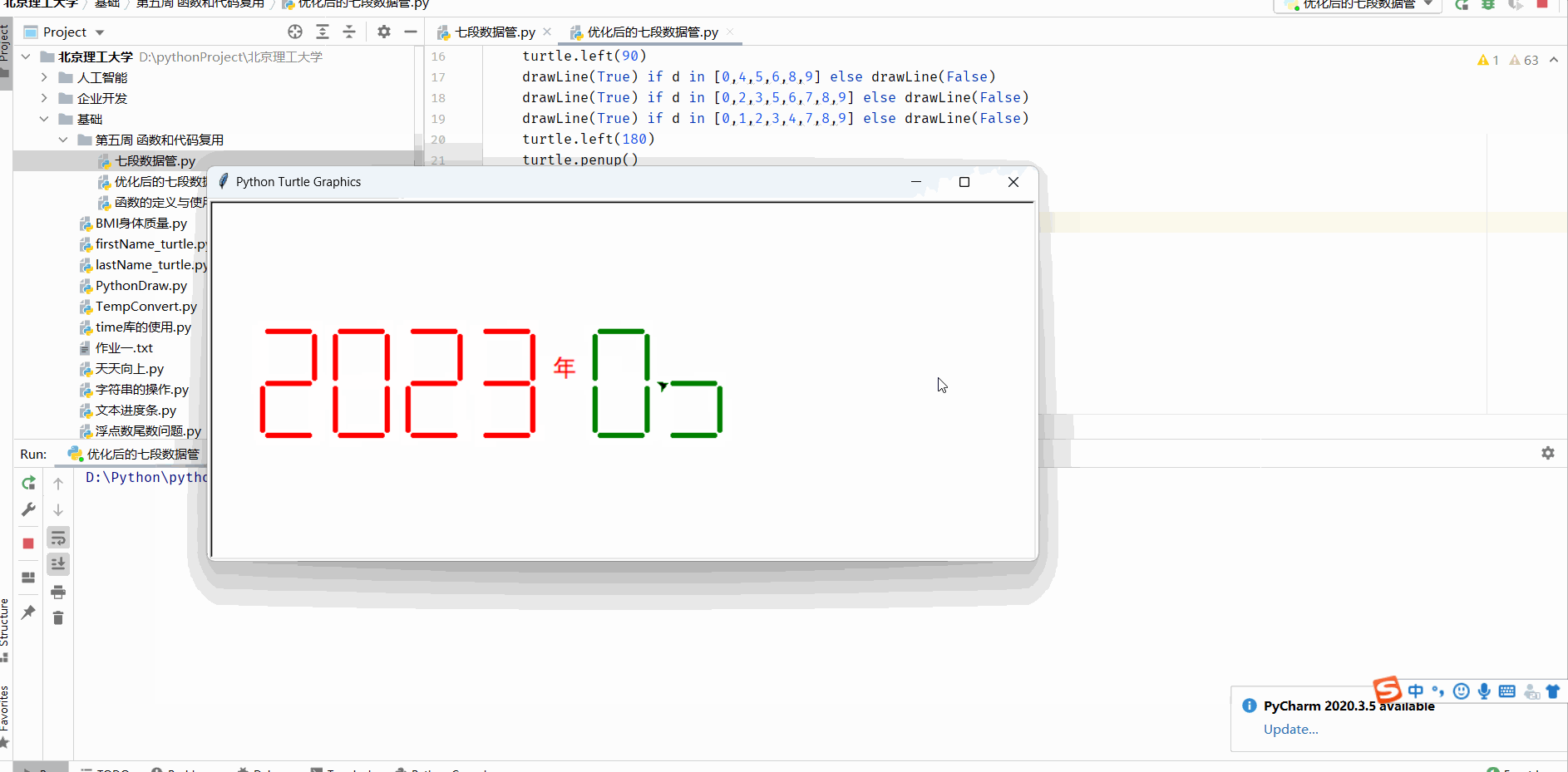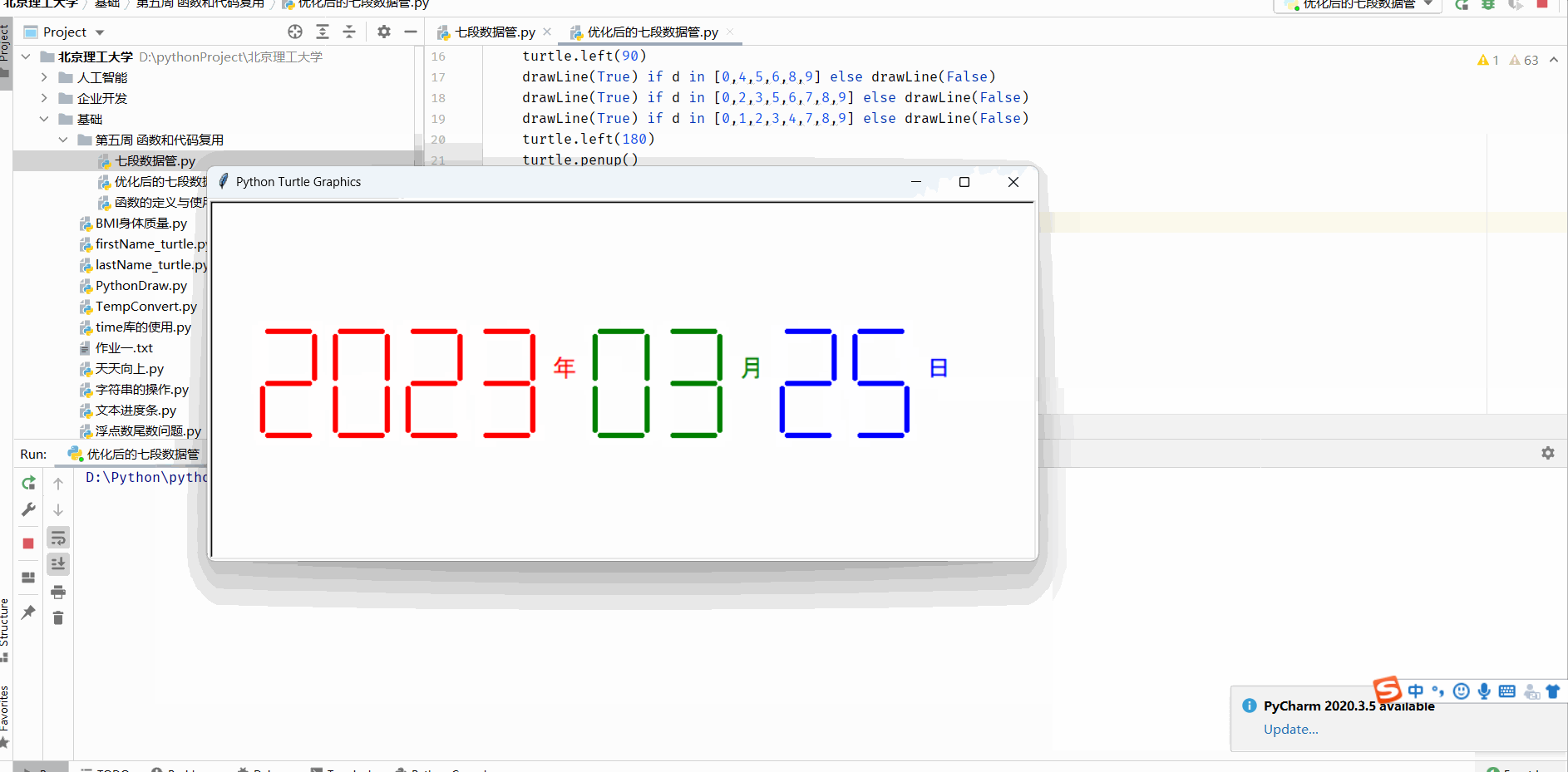
函数的定义与使用及七段数码管绘制
函数的定义 函数是一段代码的表示 函数是一段具有特定功能的、可重用的语句组 函数是一种功能的抽象,一般函数表达特定功能 两个作用:降低编程难度 和 代码复用 求一个阶乘 fact就是 函数名 n就是参数 return就是输出部分即返回值 而函数的调用就是…...

怎么压缩pdf文件大小?pdf文件太大如何压缩?
喜爱看小说的小伙伴们都会在网上下载很多的pdf格式电子书以方便随时阅览,但是pdf的电子书一般都过于的冗长,下载后的储存也是一个问题,怎么pdf压缩大小呢?可以试试今天介绍的这款pdf在线压缩工具来进行pdf压缩(https:/…...

阿里云Linux服务器登录名ecs-user和root选择问题
阿里云服务器Linux系统登录名可以选择root或ecs-user,root具有操作系统的最高权限,但是root会导致的安全风险比较大,ecs-user比较安全,但是如果系统后续依赖root权限就会比较麻烦,从安全的角度,建议选择ecs…...
,挂载配置文件使应用的配置和运行的镜像解耦)
【云原生】 初体验阿里云Serverless应用引擎SAE(三),挂载配置文件使应用的配置和运行的镜像解耦
目录 一、前言二、SAE配置1、创建配置项2、配置SAE Nginx服务效果1、【云原生】 初体验阿里云Serverless应用引擎SAE(一),部署Nginx服务 2、【云原生】 初体验阿里云Serverless应用引擎SAE(二),前端Nginx静态文件持久化到对象存储OSS 本篇 3、【云原生】 初体验阿里云Se…...
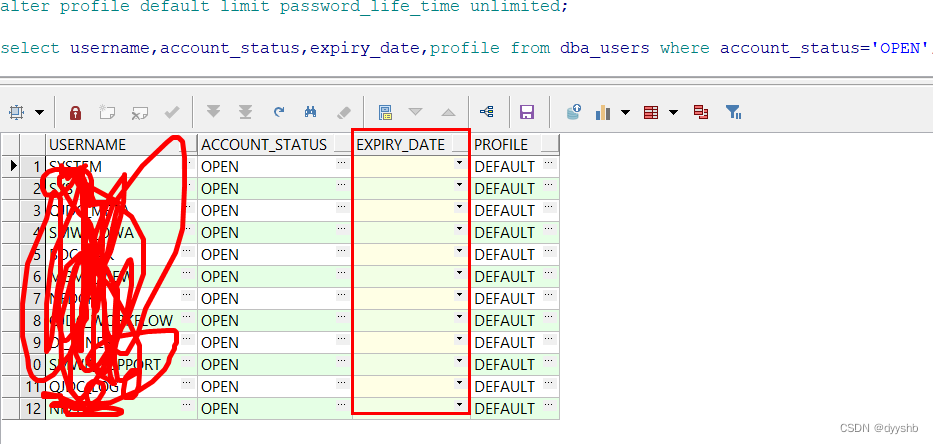
Oracle用户密码过期,修改永不过期
修改密码有效过期时间,可以通过以下四步设置,如果再第一步发现本身的密码过期时间为无限期的,那就请各位小伙伴绕过,如果发现不是无期限的,那么必须设置第四步,才会生效。 目录 第一步:查询密码…...
welearn 视听说1-4
词汇题(55道) 1. You should carefully think over_____ the manager said at the meeting. A. that B. which C. what D. whose 1.选C,考察宾语从句连接词,主句谓语动词think over后面缺宾语,后面的宾语从句谓语动…...

【git】将本地项目同步到远程
前提:git已经安装,并与账号完成密钥绑定 在github上创建一个新仓库 在项目文件夹下,右击选择git bash here ,打开一个终端对话框 git init (在项目目录下出现隐藏的.git文件夹,目的是把该项目文件夹变成git可管理…...
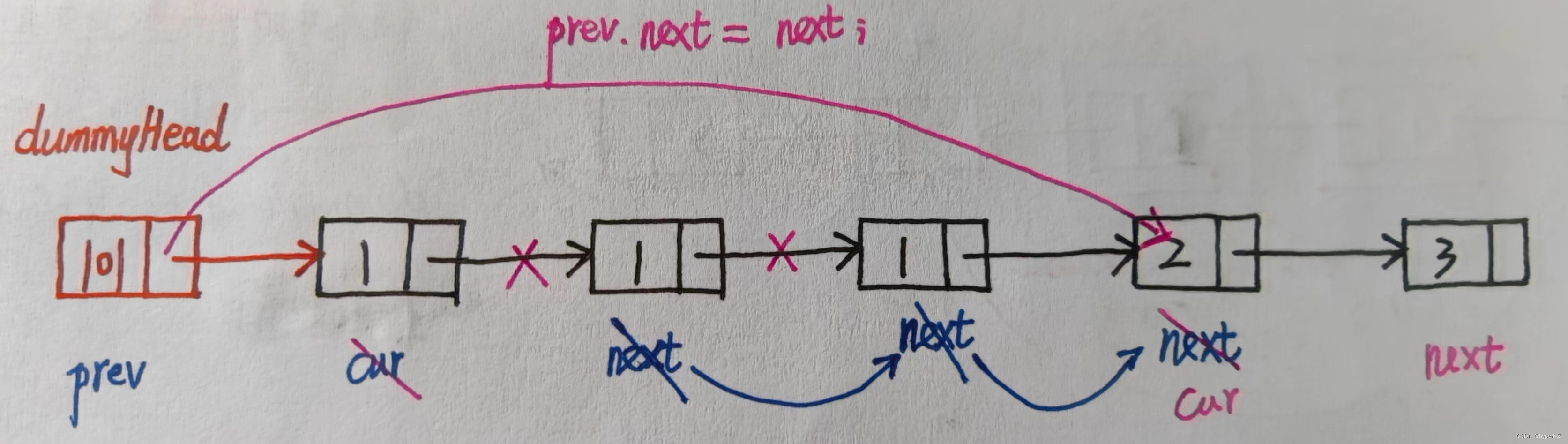
10-链表练习-LeetCode82删除排序链表中的重复元素II
题目 给定一个已排序的链表的头 head , 删除原始链表中所有重复数字的节点,只留下不同的数字 。返回已排序的链表 。 示例 1: 输入:head [1,2,3,3,4,4,5] 输出:[1,2,5] 示例 2: 输入:head …...

贯穿设计模式第五话--接口隔离原则
🥳🥳🥳 茫茫人海千千万万,感谢这一刻你看到了我的文章,感谢观赏,大家好呀,我是最爱吃鱼罐头,大家可以叫鱼罐头呦~🥳🥳🥳 从今天开始,将…...
)
C语言计算机二级/C语言期末考试 刷题(四)
在空闲时间整理了一些C语言计算机二级和C语言期末考试题库 整理不易,大家点赞收藏支持一下 祝大家计算机二级和期末考试都高分过 系列文章: C语言计算机二级/C语言期末考试 刷题(一) C语言计算机二级/C语言期末考试 刷题&#x…...

JDK8中Stream接口的常用方法
参考答案 Stream 接口中的方法分为中间操作和终端操作,具体如下。 中间操作: filter:过滤元素map:映射,将元素转换成其他形式或提取信息flatMap:扁平化流映射limit:截断流,使其元…...
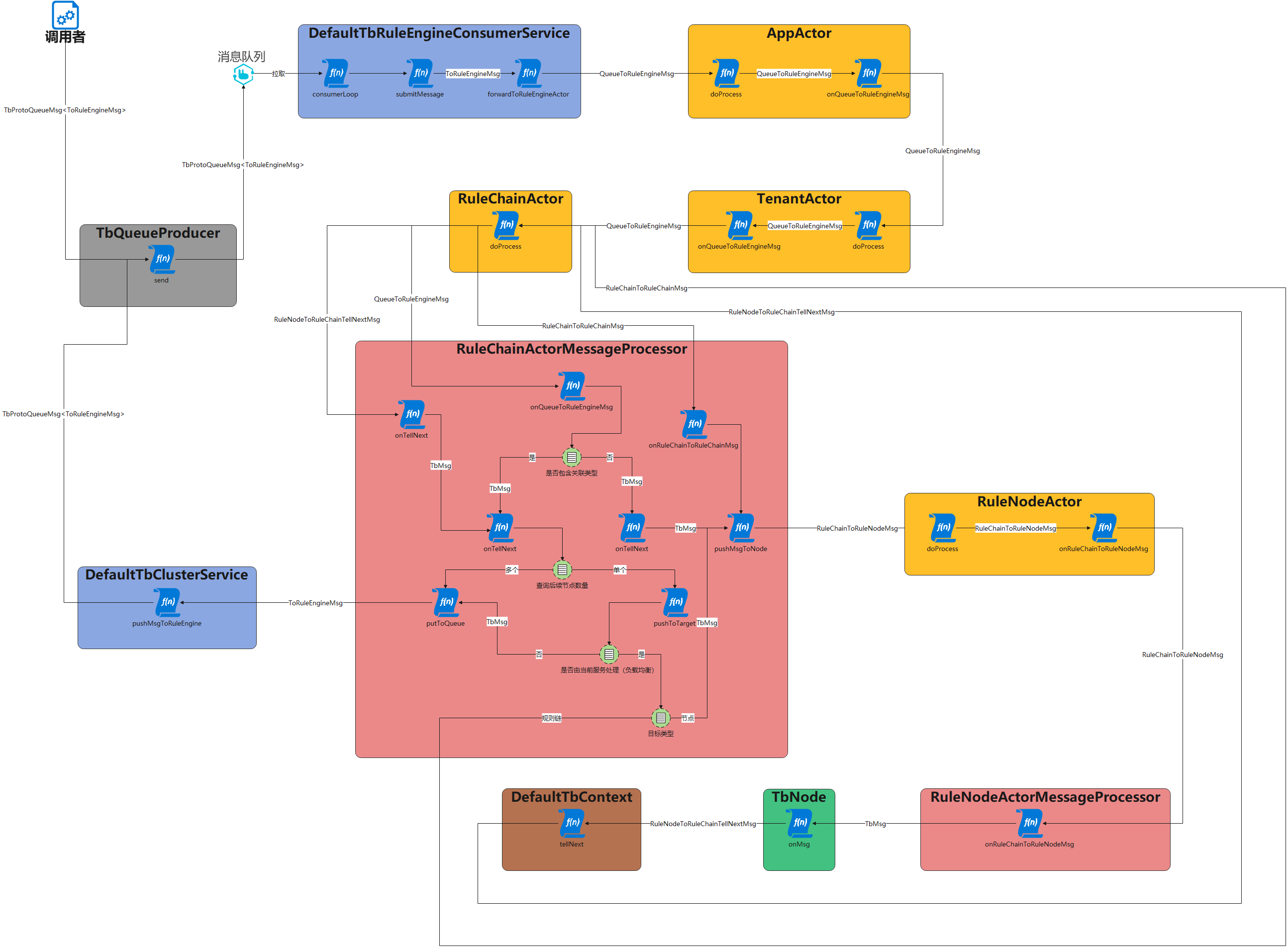
ThingsBoard源码解析-数据订阅与规则链数据处理
前言 结合本篇对规则链的执行过程进行探讨 根据之前对MQTT源码的学习,我们由消息的处理入手 //org.thingsboard.server.transport.mqtt.MqttTransportHandlervoid processRegularSessionMsg(ChannelHandlerContext ctx, MqttMessage msg) {switch (msg.fixedHeade…...

探究Transformer模型中不同的池化技术
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...
