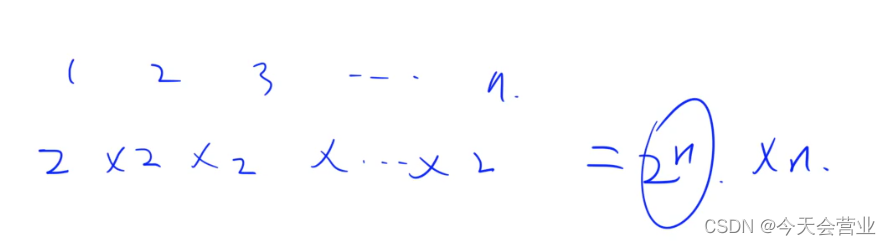递归:斐波那契数列、递归实现指数型枚举、递归实现排列型枚举
递归:O(2^n)
调用自己
例题及代码模板:
斐波那契数列
输入一个整数 n ,求斐波那契数列的第 n 项。
假定从 0 开始,第 0 项为 0。
数据范围
0≤n≤39
样例
输入整数 n=5 返回 5#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;int Fibonacci(int n){if(n==0) return 0;if(n==1) return 1;if(n==2) return 1;return Fibonacci(n-1)+Fibonacci(n-2);
}
int main(){int n;cin>>n;cout<<Fibonacci(n)<<endl;return 0;
} O(n*2^n)
递归实现指数型枚举
从 1∼n 这 n 个整数中随机选取任意多个,输出所有可能的选择方案。
输入格式
输入一个整数 n。
输出格式
每行输出一种方案。
同一行内的数必须升序排列,相邻两个数用恰好 1 个空格隔开。
对于没有选任何数的方案,输出空行。
本题有自定义校验器(SPJ),各行(不同方案)之间的顺序任意。
数据范围
1≤n≤15
输入样例:
3
输出样例:
3
2
2 3
1
1 3
1 2
1 2 3#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=15;
int n;
int st[N];
void dfs(int u){if(u==n){for(int i=0;i<n;i++){if(st[i]==1)cout<<i+1<<" ";}cout<<endl;return ;}st[u]=2;dfs(u+1);st[u]=0;st[u]=1;dfs(u+1);st[u]=0;
}int main(){cin>>n;dfs(0); return 0;
}递归实现排列型枚举
把 1∼n这 n个整数排成一行后随机打乱顺序,输出所有可能的次序。
输入格式
一个整数 n。
输出格式
按照从小到大的顺序输出所有方案,每行 1 个。
首先,同一行相邻两个数用一个空格隔开。
其次,对于两个不同的行,对应下标的数一一比较,字典序较小的排在前面。
数据范围
1≤n≤9
输入样例:
3
输出样例:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1时间复杂度:
一共递归n层:
第一层是:O(n)
第二层:有n个分支,每个分支有一个for循环,即O(n*n)
第三层:有n*(n-1)个分支,每个分支有一个for循环,即O(n*(n-1)*n)
……
第n层(叶节点):有n!个分支,每个分支有一个for循环,即O(n!*n)
所以总的时间复杂度为:n(1+n+n(n-1)+……+n!)
(1+n+n(n-1)+……+n!)等价于:(n!+n!/1+n!/(1*2)+n!/(1*2*3)+……+n!/(n-1)!+n!/n!);首先这个等式一定大于n!且小于(n!+n!/1+n!/2+n!/4+……+n!/2^(n-1)+n!/2^n)即3n!
所以这道题的时间复杂度为O(3n*n!),即O(n*n!)
#include<cstring>
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=10;
int n,state[N];
bool used[N];
void dfs(int u) {if(u>n) {for(int i=1; i<=n; i++)cout<<state[i]<<" ";cout<<endl;return ;}for(int i=1; i<=n; i++) {if(!used[i]) {state[u]=i;used[i]=true;dfs(u+1);state[u]=0;used[i]=false;}}
}
int main() {cin>>n;dfs(1);return 0;
}递归实现组合型枚举
带分数
相关文章:

递归:斐波那契数列、递归实现指数型枚举、递归实现排列型枚举
递归:O(2^n) 调用自己 例题及代码模板: 斐波那契数列 输入一个整数 n ,求斐波那契数列的第 n 项。 假定从 0 开始,第 0 项为 0。 数据范围 0≤n≤39 样例 输入整数 n5 返回 5 #include <iostream> #include <cstring&g…...

oracle模糊查询时字段内容包含下划线的解决办法
最近项目中遇到一个关于模糊查询问题。表tabA中的字段name的值有下划线的情况,在模糊查询时发现查询的记录不对。 表的结构 表名:tabA id name sex 1 test_601 1 2 test_602 2 3 test16 1 4 t…...

C++:explicit关键字
C中的explicit关键字只能用于修饰只有一个参数的类构造函数,它的作用是表明该构造函数是显示的,而非隐式的,跟它相对应的另一个关键字是implicit,意思是隐藏的,类构造函数默认情况下即声明为implicit(隐式)。那么显示声…...

【C5】bmc wtd,post
文章目录1.bmc_wtd_cpld:syscpld.c中wd_en和wd_kick节点对应寄存器,crontab,FUNCNAME2.AST芯片WDT切换主备:BMC用WDT2作为主备切换的控制器2.1 AC后读取:bmc处于主primary flash(设完后:实际主&…...
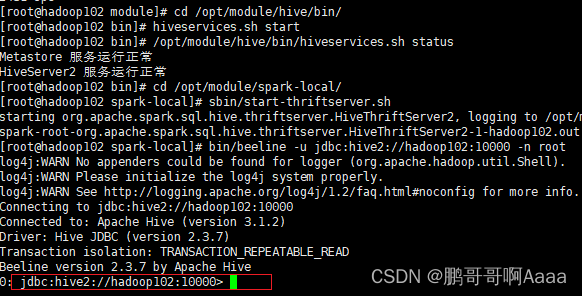
200.Spark(七):SparkSQL项目实战
一、启动环境 需要启动mysql,hadoop,hive,spark。并且能让spark连接上hive(上一章有讲) #启动mysql,并登录,密码123456 sudo systemctl start mysqld mysql -uroot -p#启动hive cd /opt/module/ myhadoop.sh start#查看启动情况 jpsall#启动hive cd /opt/module/hive/…...
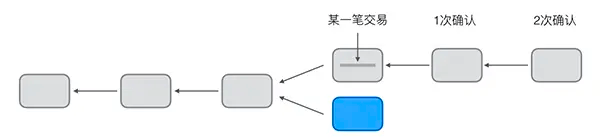
区块链系统:挖矿原理
在比特币的P2P网络中,有一类节点,它们时刻不停地进行计算,试图把新的交易打包成新的区块并附加到区块链上,这类节点就是矿工。因为每打包一个新的区块,打包该区块的矿工就可以获得一笔比特币作为奖励。所以,…...

【博弈】【清华冬令营2018模拟】取石子
写完敢说全网没有这么详细的题解了。 注意:题解长是为了方便理解,所以读起来速度应该很快。 题目描述 有 nnn 堆石子,第 iii 堆有 xix_ixi 个。 AliceAliceAlice 和 BobBobBob 轮流去石子(先后手未定), …...
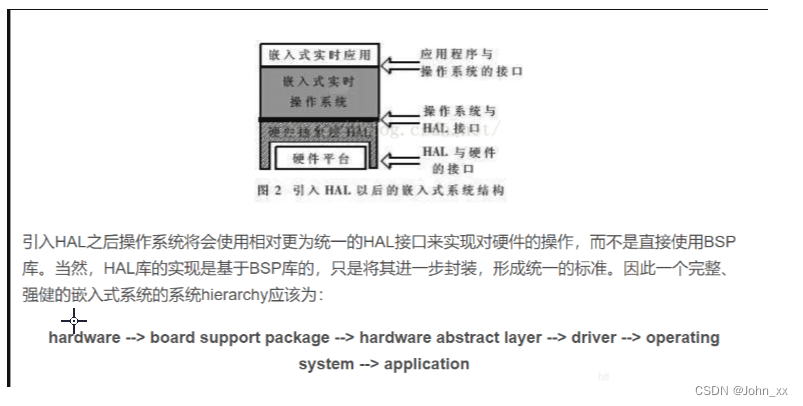
嵌入式:BSP的理解
BSP概念总结BSP定义BSP的特点BSP的主要工作BSP在嵌入式系统和Windowsx系统中的不同BSP和PC机主板上的BIOS区别BSP与 HAL关系嵌入式计算机系统主要由 硬件层,中间层,系统软件层和应用软件层四层组成。硬件层:包含CPU,存储器(SDRAM&…...
Linux主机Tcpdump使用-centos实例
1、安装前系统信息 ifconfig查看系统网络接口情况。这里可以看到3个interface,ens160是正常使用的网口,lo是主机的loopback地址127.0.0.1。另外,由于centos安装在虚拟主机上,virbr0是KVM默认创建的一个Bridge,其作用是为连接其上的…...
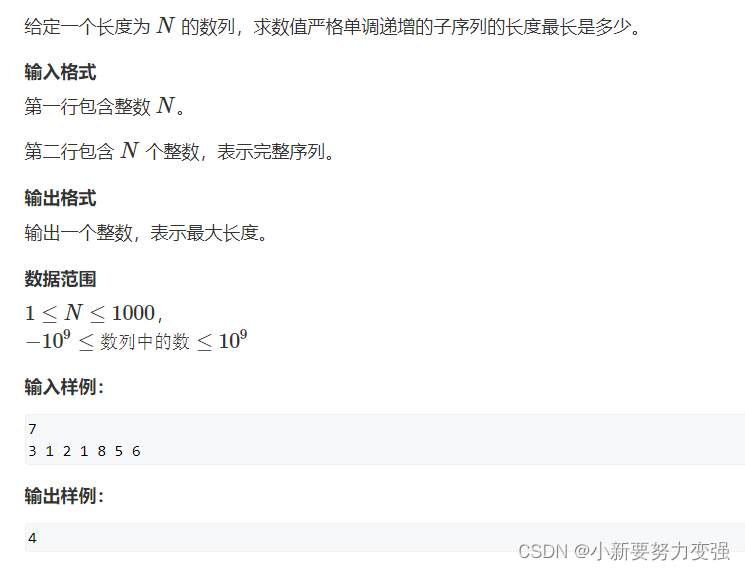
线性DP——AcWing 898. 数字三角形、AcWing 895. 最长上升子序列
AcWing 898. 数字三角形 1.题目 898. 数字三角形 2.思路 DP问题首先考虑状态转移方程,定义一个集合f ( i , j) ,表示从第一个数字(1,1)走到第 i行,第 j列(i , j)的所有方案的集合,…...
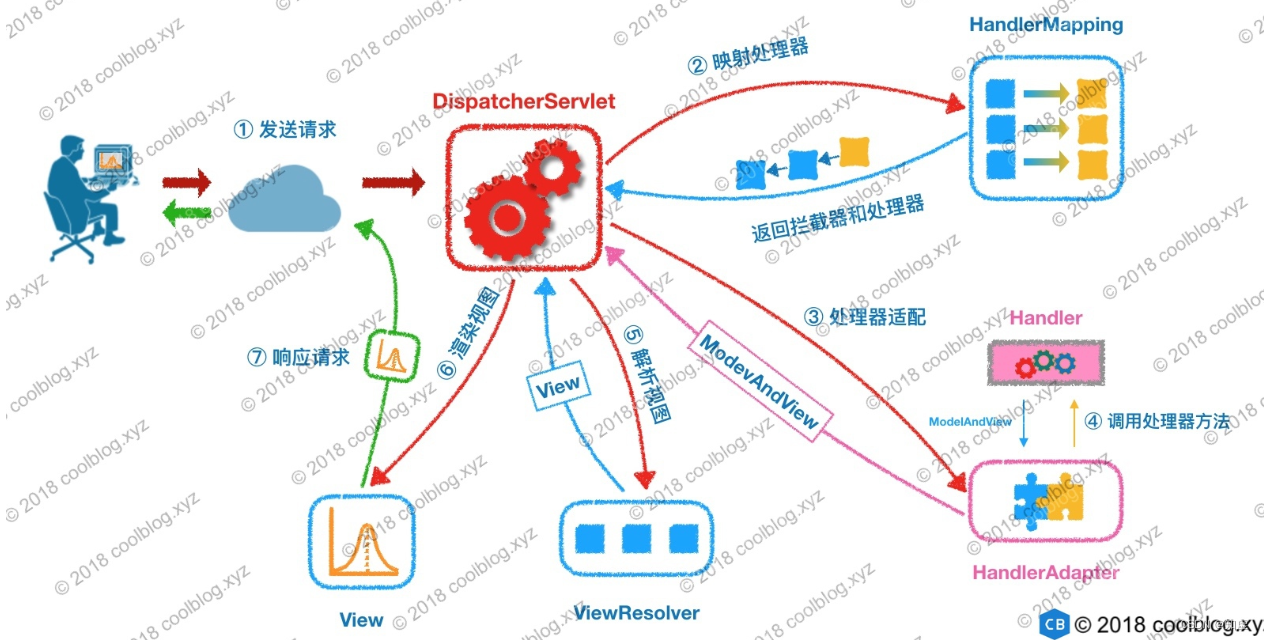
SpringMVC
SpringMVC配置 引入Maven依赖 (springmvc)web.xml配置DispatcherServlet配置 applicationContext 的 MVC 标记开发Controller控制器 几点注意事项: 在web.xml中 配置<load-on-startup> 0 </load-on-startup> 会自动创建Spring…...
)
C++模板基础(二)
函数模板(二) ● 模板实参的类型推导 – 如果函数模板在实例化时没有显式指定模板实参,那么系统会尝试进行推导 template<typename T> void fun(T input, T input2) {std::cout << input << \t << input2 << …...
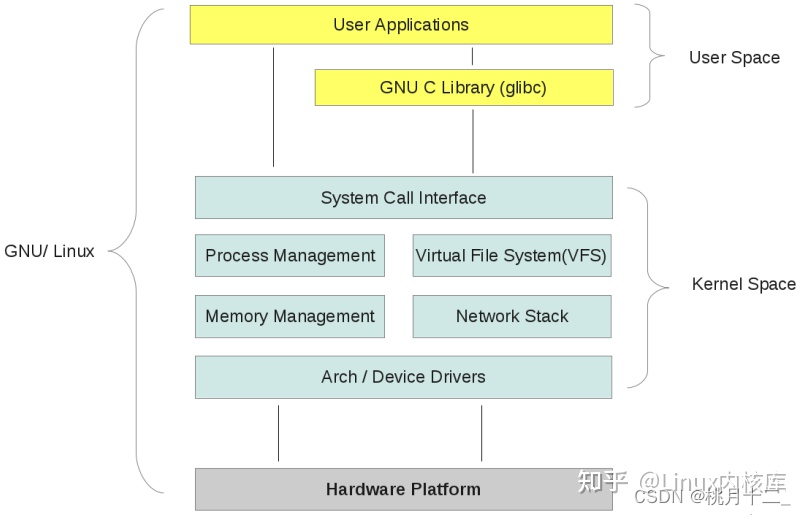
什么是linux内核态、用户态?
目录标题为什么需要区分内核空间与用户空间内核态与用户态如何从用户空间进入内核空间整体结构为什么需要区分内核空间与用户空间 在 CPU 的所有指令中,有些指令是非常危险的,如果错用,将导致系统崩溃,比如清内存、设置时钟等。如…...

day8—选择题
文章目录1.Test.main() 函数执行后的输出是(D)2. JUnit主要用来完成什么(D)3.下列选项中关于Java中super关键字的说法正确的是(A)1.Test.main() 函数执行后的输出是(D) public clas…...
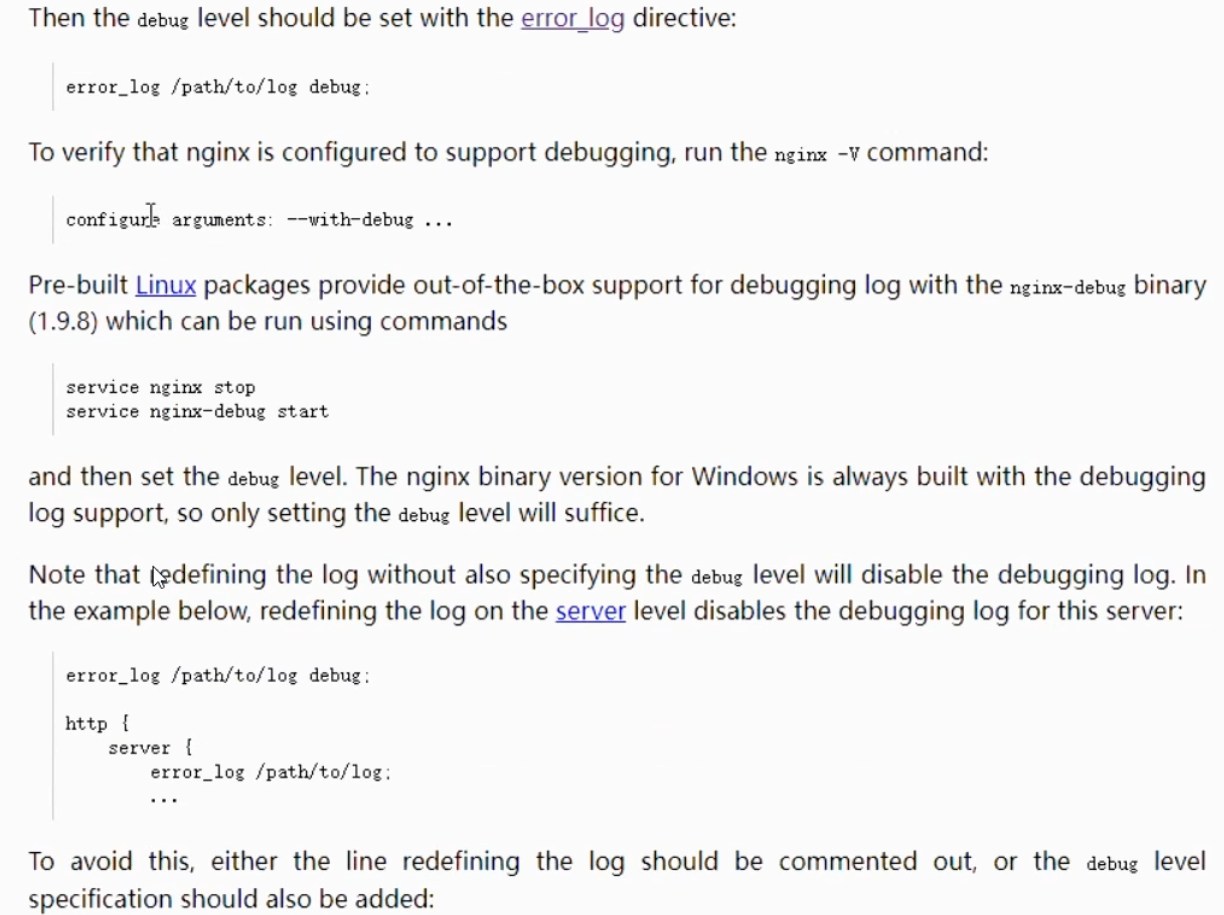
ngx错误日志error_log配置
ngx之error_log 日志配置格式: 常见的错误日志级别 错误日志可配置位置 关闭error_log配置 设置debug 日志级别的前提: ngx之error_log 日志配置格式: error_log 存放路径 日志级别 例: error_log /usr/local/log…...

1.11、自动化
自动化 一、java 手机自动化 首先new DesertCapabilities(这是一个类) setCapability – 设置信息 获取appium的驱动对象 new AppiumDriver – 本机IP地址:端口号/wd/hub,前面的设置值信息 driver.findElementById() – 通过id找位置 click() – 点击 &…...
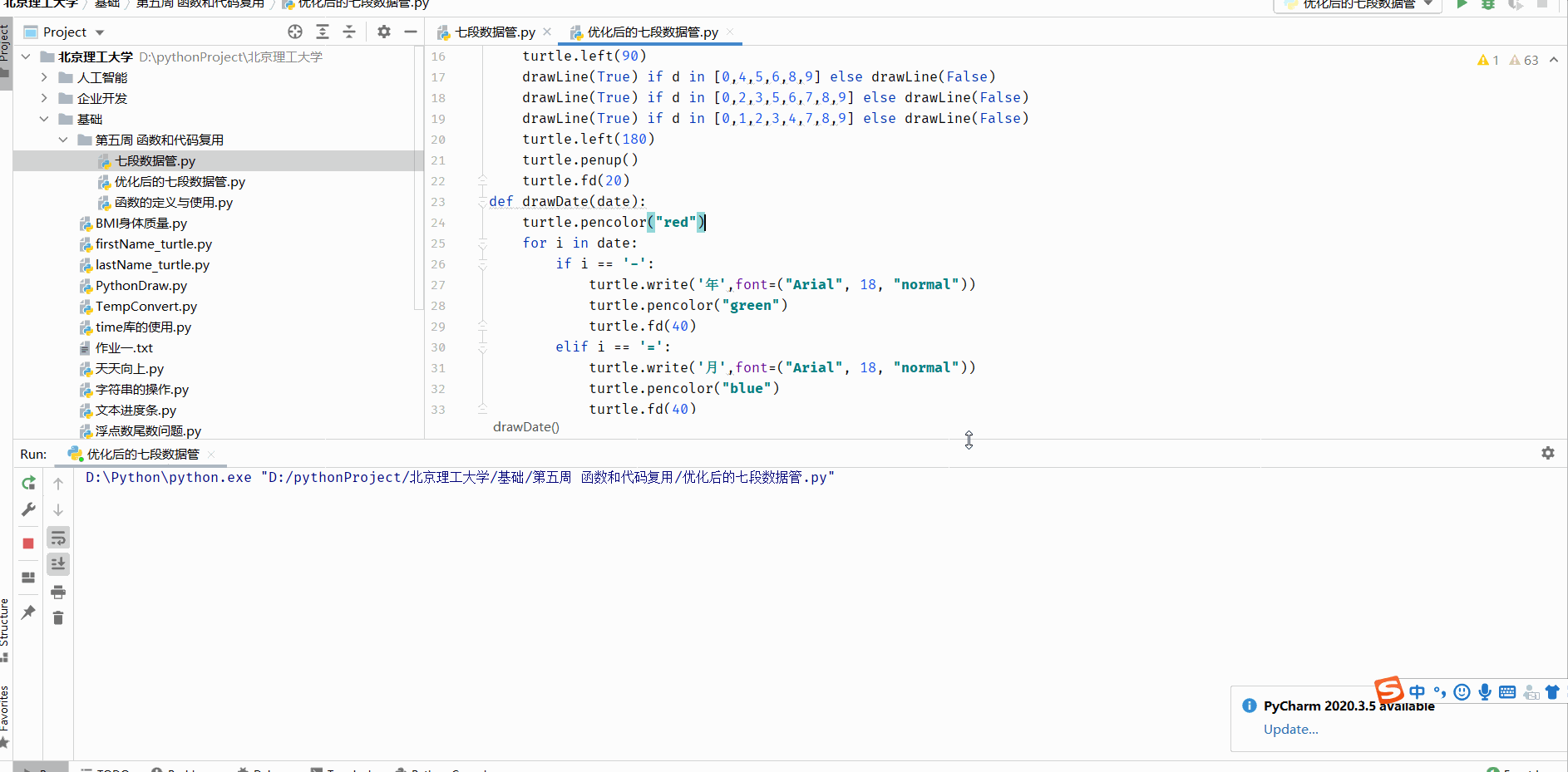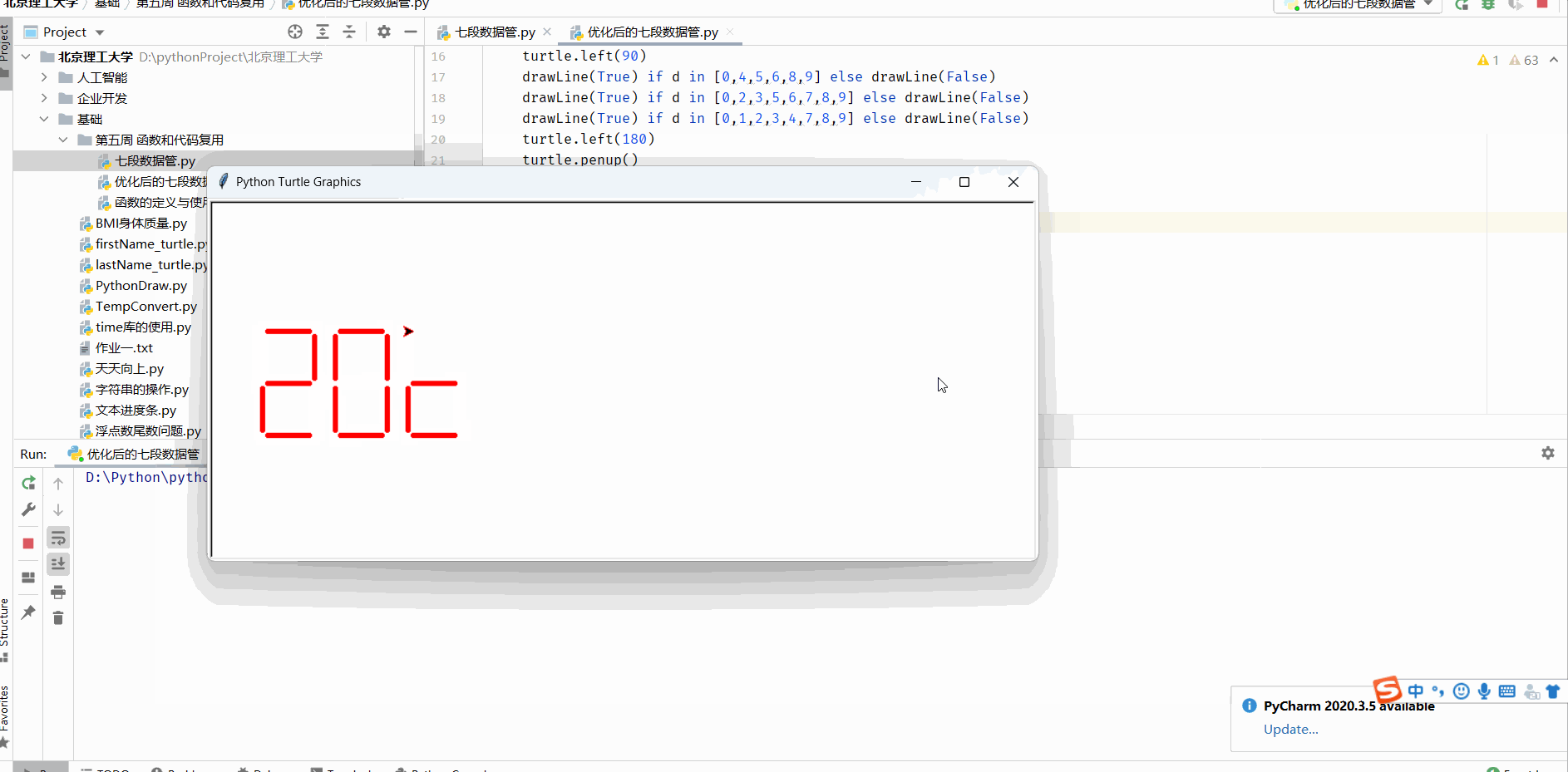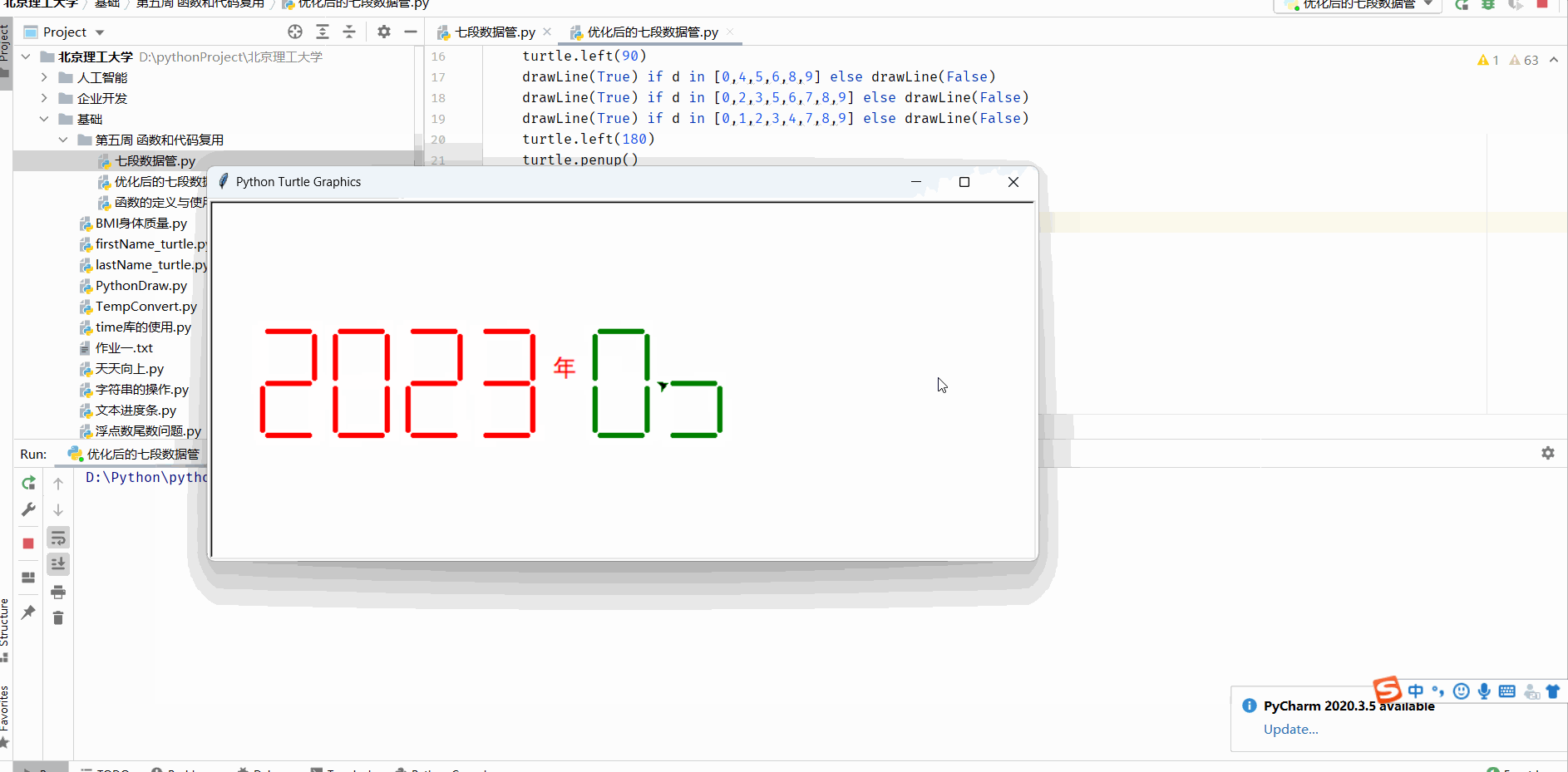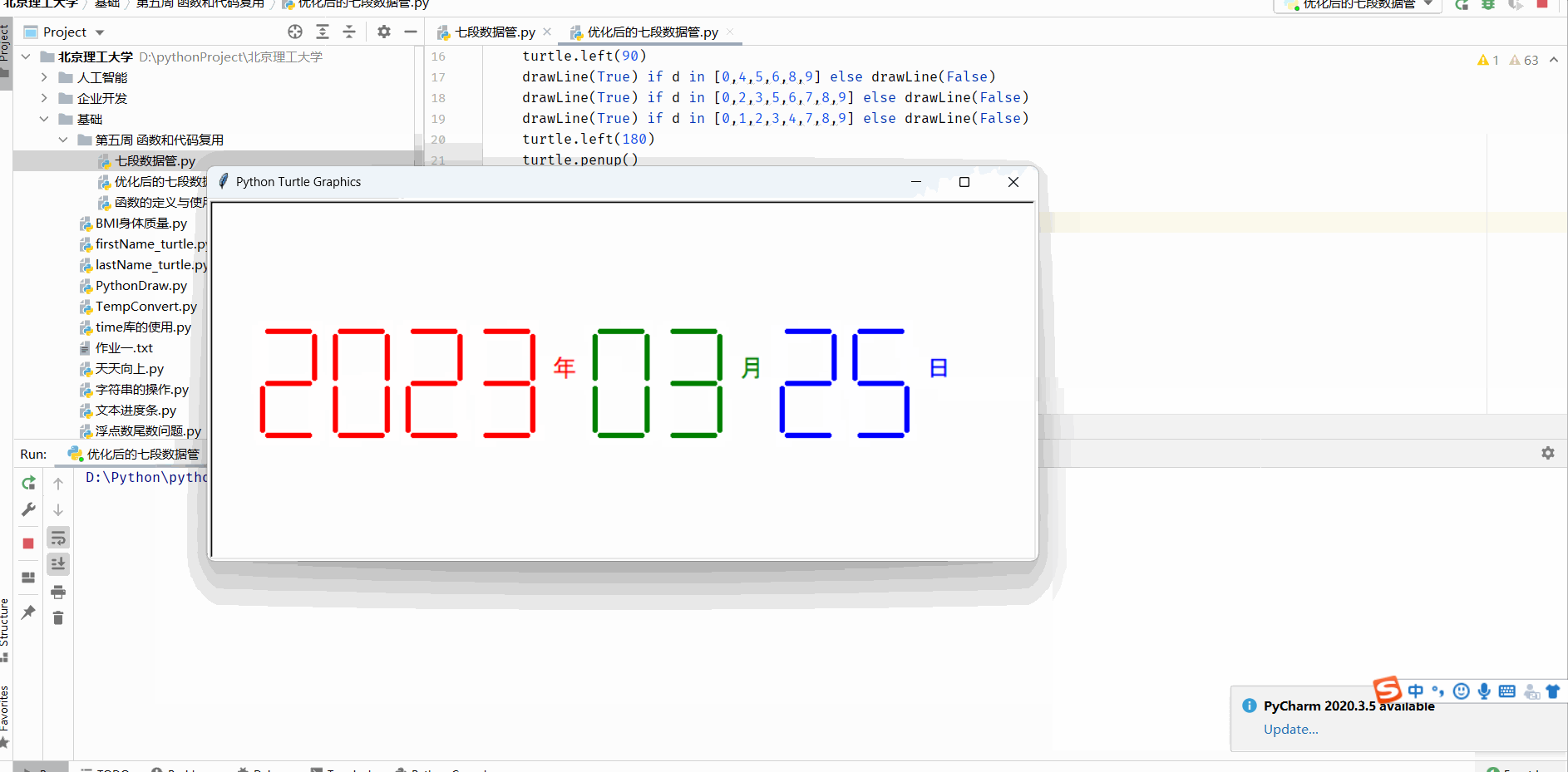
函数的定义与使用及七段数码管绘制
函数的定义 函数是一段代码的表示 函数是一段具有特定功能的、可重用的语句组 函数是一种功能的抽象,一般函数表达特定功能 两个作用:降低编程难度 和 代码复用 求一个阶乘 fact就是 函数名 n就是参数 return就是输出部分即返回值 而函数的调用就是…...

怎么压缩pdf文件大小?pdf文件太大如何压缩?
喜爱看小说的小伙伴们都会在网上下载很多的pdf格式电子书以方便随时阅览,但是pdf的电子书一般都过于的冗长,下载后的储存也是一个问题,怎么pdf压缩大小呢?可以试试今天介绍的这款pdf在线压缩工具来进行pdf压缩(https:/…...

阿里云Linux服务器登录名ecs-user和root选择问题
阿里云服务器Linux系统登录名可以选择root或ecs-user,root具有操作系统的最高权限,但是root会导致的安全风险比较大,ecs-user比较安全,但是如果系统后续依赖root权限就会比较麻烦,从安全的角度,建议选择ecs…...
,挂载配置文件使应用的配置和运行的镜像解耦)
【云原生】 初体验阿里云Serverless应用引擎SAE(三),挂载配置文件使应用的配置和运行的镜像解耦
目录 一、前言二、SAE配置1、创建配置项2、配置SAE Nginx服务效果1、【云原生】 初体验阿里云Serverless应用引擎SAE(一),部署Nginx服务 2、【云原生】 初体验阿里云Serverless应用引擎SAE(二),前端Nginx静态文件持久化到对象存储OSS 本篇 3、【云原生】 初体验阿里云Se…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...