【博弈】【清华冬令营2018模拟】取石子
写完敢说全网没有这么详细的题解了。
注意:题解长是为了方便理解,所以读起来速度应该很快。
题目描述
有 nnn 堆石子,第 iii 堆有 xix_ixi 个。 AliceAliceAlice 和 BobBobBob 轮流去石子(先后手未定), AliceAliceAlice 每次从一堆中取走 aaa 个,BobBobBob 每次从一堆中取走 bbb 个,无法操作者输。不难发现只会有四种情况:AliceAliceAlice 必胜,BobBobBob 必胜,先手必胜,后手必胜。你需选定若干堆石子(共有 2n2^n2n 钟方案),AliceAliceAlice 和 BobBobBob 只能在你选出的堆中取,问四种情况对应的方案数。
输入格式
第一行三个整数 n,a,bn,a,bn,a,b。
第二行 nnn 个整数 x1,x2,...,xnx_1,x_2,...\ ,x_nx1,x2,... ,xn
输出格式
一行四个整数,分别表示 AliceAliceAlice 必胜,BobBobBob 必胜,先手必胜,后手必胜的方案数,对 109+710^9+7109+7 取模。
样例
输入样例1
2 2 3
2 3
输出样例1
2 0 1 1
样例解释1
数据范围与提示
对于 10%10\%10% 的数据,n,xi≤5n,x_i\le5n,xi≤5。
对于 50%50\%50% 的数据,n≤20n\le20n≤20。
对于另外 10%10\%10% 的数据,a=ba=ba=b。
对于又另外 20%20\%20% 的数据,a=1a=1a=1。
对于 100%100\%100% 的数据,1≤n≤105,1≤a,b,xi≤1091\le n \le 10^5,1\le a,b,x_i\le 10^91≤n≤105,1≤a,b,xi≤109。
分析
考场没有认真分析,考后知道要分类讨论后就打出来了。
不讲部分分了,因为除了第三条其他的应该也都不会去想。
值得一提的是,当 a=ba=ba=b 时的情况还是有一定启发性的,这告诉我们往奇偶性上面想。
方面处理,我们设 a<ba<ba<b。
每堆石子对 a+ba+ba+b 取模,然后可以分四种情况:
1. xi<ax_i<axi<a,没用,但仅存在这种石堆时后手必胜。
2. a≤xi<ba\le x_i<ba≤xi<b,只要存在即 aaa 获胜。
3. b≤xi<2ab\le x_i< 2ab≤xi<2a,只和奇偶性有关。
4. 2a≤xi2a\le x_i2a≤xi,
- 1. 若不存在且 (3) 为奇数个则先手必胜
- 2. 若不存在且 (3) 为偶数个则后手必胜
- 3. 若存在两个及以上则 aaa 必胜
- 4. 若仅存在一个且 (3) 为奇数个则 aaa 必胜
- 5. 若仅存在一个且 (3) 为偶数个则先手必胜
1~3 都好理解,4 的 1,2 也好理解;
对于4-3,因为无论如何 bbb 均无法阻止 aaa 将局面转化成 (2) 的情况,所以 aaa 必胜;
对于4-4,相当于在 3 为奇数的情况下多了一个 2a≤xi2a\le x_i2a≤xi,注意到此时该堆 aaa 可多次取石,我们对 a,ba,ba,b 两人分别讨论:
- 对于 aaa 先手,先取 2a≤xi2a\le x_i2a≤xi 的一堆,之后把这一堆搁在一旁,就变成了 4-1 的情况,即 bbb 获胜,但最后 aaa 再取搁在一旁的这堆,此时 bbb 无法再取,aaa 获胜。
- 而对于 bbb 先手,因为对于 2a≤xi2a\le x_i2a≤xi 的一堆,bbb 仍然最多只能取一次,所以对于 bbb 而言,场上局面依旧是 4-2(奇数堆 + 2a≤xi2a\le x_i2a≤xi 一堆 = 偶数堆),此时后手 aaa 获胜。
再分析 4-5,类似的,我们堆 a,ba,ba,b 两人分别讨论:
- 对于 aaa 先手,无论怎么选都能使 bbb 进入4-2 的必输状态,aaa 获胜。
- 对于 bbb 先手,当且仅当其最初选 2a≤xi2a\le x_i2a≤xi 时可使 aaa 进入 4-2 的必输状态,因为默认玩家很聪明,所以 bbb 获胜。
思维量很小,于是就可以打了。
#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef long long LL;
const int N=1e5+5,M=1e9+7;
int n,a,b,Bz,x[N],fac[N],inv[N];
inline int Rd(){int s=0,w=1;char ch=getchar();while (ch<'0'||ch>'9'){if(ch=='-') w=-1;ch=getchar();}while (ch>='0'&&ch<='9') s=(s<<1)+(s<<3)+ch-'0',ch=getchar();return s*w;}
int qp(int A,int B){int res=1;while (B){if(B&1) res=1ll*res*A%M;A=1ll*A*A%M;B>>=1;}return res;
}
void init(){fac[0]=inv[0]=1;for(int i=1;i<=n;i++) fac[i]=1ll*fac[i-1]*i%M;inv[n]=qp(fac[n],M-2);for(int i=n-1;i>=1;i--) inv[i]=1ll*inv[i+1]*(i+1)%M;return ;
}
int C(int A,int B){if(A<B) return 0;return 1ll*fac[A]*inv[B]%M*inv[A-B]%M;
}
signed main(){// freopen("stone.in","r",stdin);// freopen("stone.out","w",stdout);n=Rd();a=Rd();b=Rd();init();for(int i=1;i<=n;i++) x[i]=Rd();int c1=0,c2=0,c3=0,c4=0;LL ans1=0,ans2=0,ans3=0,ans4=0;if(a>b) swap(a,b),Bz=1;for(int i=1;i<=n;i++){x[i]%=(a+b);if(x[i]<a) c1++;if(x[i]>=a&&x[i]<b) c2++;else if(x[i]>=b&&x[i]<2*a) c3++;else if(2*a<=x[i]) c4++;}// printf("%d %d %d %d\n",c1 ,c2,c3,c4);int nw=qp(2,n-c2);for(int i=1;i<=c2;i++) (ans1+=1ll*C(c2,i)*nw%M)%=M; //a<=x[i]<b, A winnw=qp(2,n-c2-c4);for(int i=2;i<=c4;i++) (ans1+=1ll*C(c4,i)*nw%M)%=M; //2a<=x[i], at least 2, A winans4=qp(2,c1);int C1=qp(2,c1);for(int i=0;i<=(c3-1)/2;i++) (ans3+=1ll*C(c3,2*i+1)*C1%M)%=M;//b<=x[i]<2a, c4=0, First win// printf("%lld\n",ans3);for(int i=1;i<=c3/2;i++) (ans4+=1ll*C(c3,2*i)*C1%M)%=M; //b<=x[i]<2a, c4=0, Second winfor(int i=0;i<=c3/2;i++) (ans3+=1ll*c4*C(c3,2*i)%M*C1%M)%=M; //c4=1, c3&1=0, First win// printf("%lld\n",ans3);for(int i=0;i<=(c3-1)/2;i++) (ans1+=1ll*c4*C(c3,2*i+1)%M*C1%M)%=M;//c4=1,c3&1=1, A winif(Bz) swap(ans1,ans2);printf("%lld %lld %lld %lld\n",ans1,ans2,ans3,ans4);return 0;
}
相关文章:

【博弈】【清华冬令营2018模拟】取石子
写完敢说全网没有这么详细的题解了。 注意:题解长是为了方便理解,所以读起来速度应该很快。 题目描述 有 nnn 堆石子,第 iii 堆有 xix_ixi 个。 AliceAliceAlice 和 BobBobBob 轮流去石子(先后手未定), …...
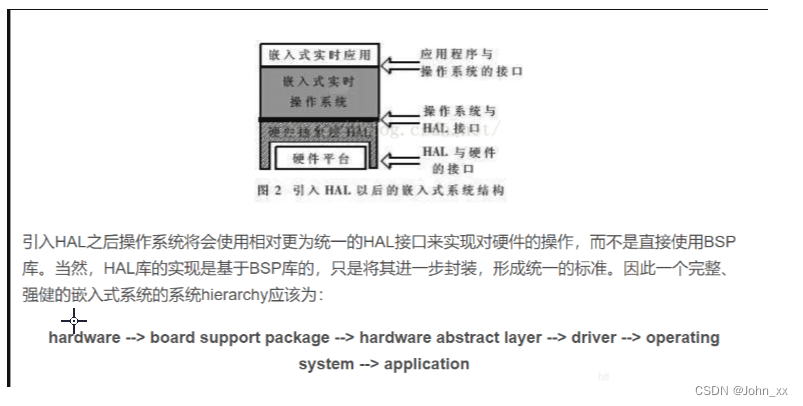
嵌入式:BSP的理解
BSP概念总结BSP定义BSP的特点BSP的主要工作BSP在嵌入式系统和Windowsx系统中的不同BSP和PC机主板上的BIOS区别BSP与 HAL关系嵌入式计算机系统主要由 硬件层,中间层,系统软件层和应用软件层四层组成。硬件层:包含CPU,存储器(SDRAM&…...
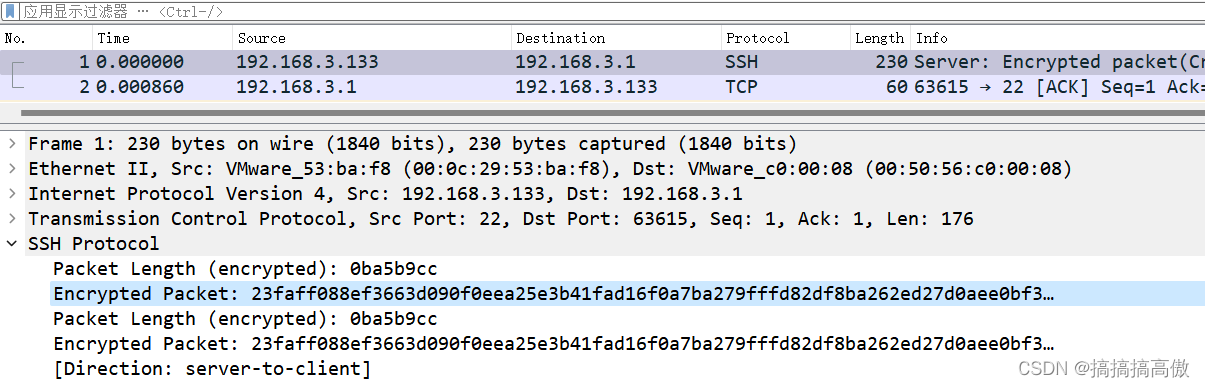
Linux主机Tcpdump使用-centos实例
1、安装前系统信息 ifconfig查看系统网络接口情况。这里可以看到3个interface,ens160是正常使用的网口,lo是主机的loopback地址127.0.0.1。另外,由于centos安装在虚拟主机上,virbr0是KVM默认创建的一个Bridge,其作用是为连接其上的…...
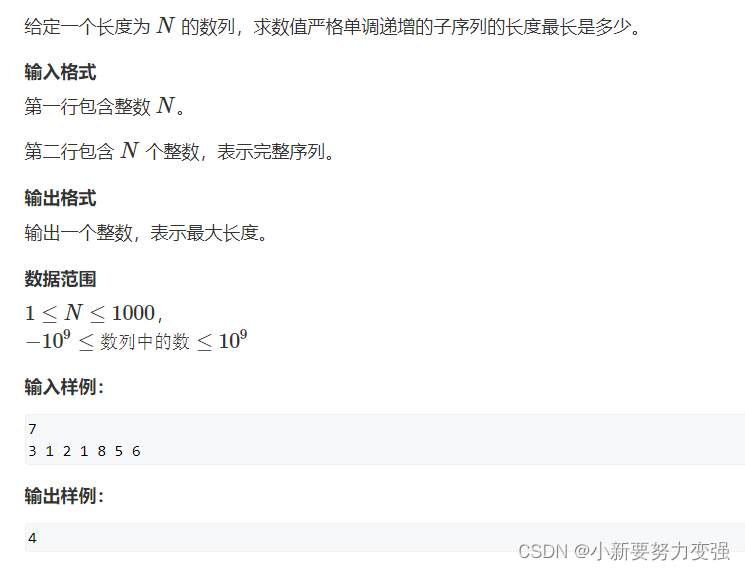
线性DP——AcWing 898. 数字三角形、AcWing 895. 最长上升子序列
AcWing 898. 数字三角形 1.题目 898. 数字三角形 2.思路 DP问题首先考虑状态转移方程,定义一个集合f ( i , j) ,表示从第一个数字(1,1)走到第 i行,第 j列(i , j)的所有方案的集合,…...
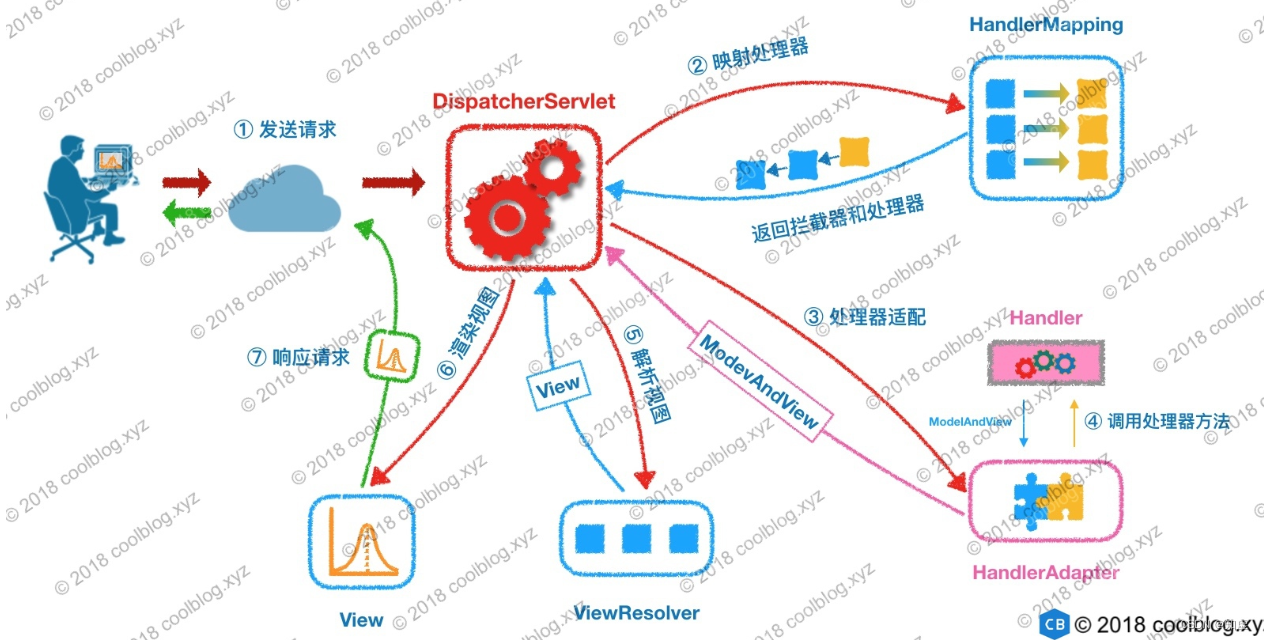
SpringMVC
SpringMVC配置 引入Maven依赖 (springmvc)web.xml配置DispatcherServlet配置 applicationContext 的 MVC 标记开发Controller控制器 几点注意事项: 在web.xml中 配置<load-on-startup> 0 </load-on-startup> 会自动创建Spring…...
)
C++模板基础(二)
函数模板(二) ● 模板实参的类型推导 – 如果函数模板在实例化时没有显式指定模板实参,那么系统会尝试进行推导 template<typename T> void fun(T input, T input2) {std::cout << input << \t << input2 << …...
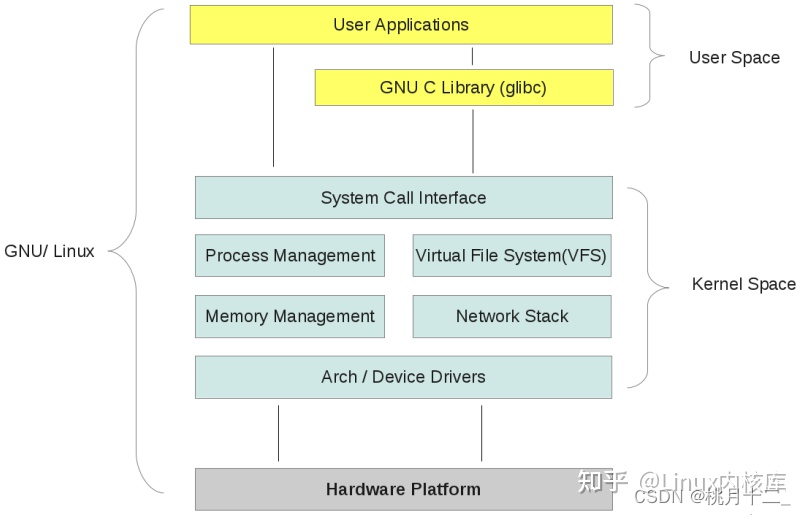
什么是linux内核态、用户态?
目录标题为什么需要区分内核空间与用户空间内核态与用户态如何从用户空间进入内核空间整体结构为什么需要区分内核空间与用户空间 在 CPU 的所有指令中,有些指令是非常危险的,如果错用,将导致系统崩溃,比如清内存、设置时钟等。如…...

day8—选择题
文章目录1.Test.main() 函数执行后的输出是(D)2. JUnit主要用来完成什么(D)3.下列选项中关于Java中super关键字的说法正确的是(A)1.Test.main() 函数执行后的输出是(D) public clas…...
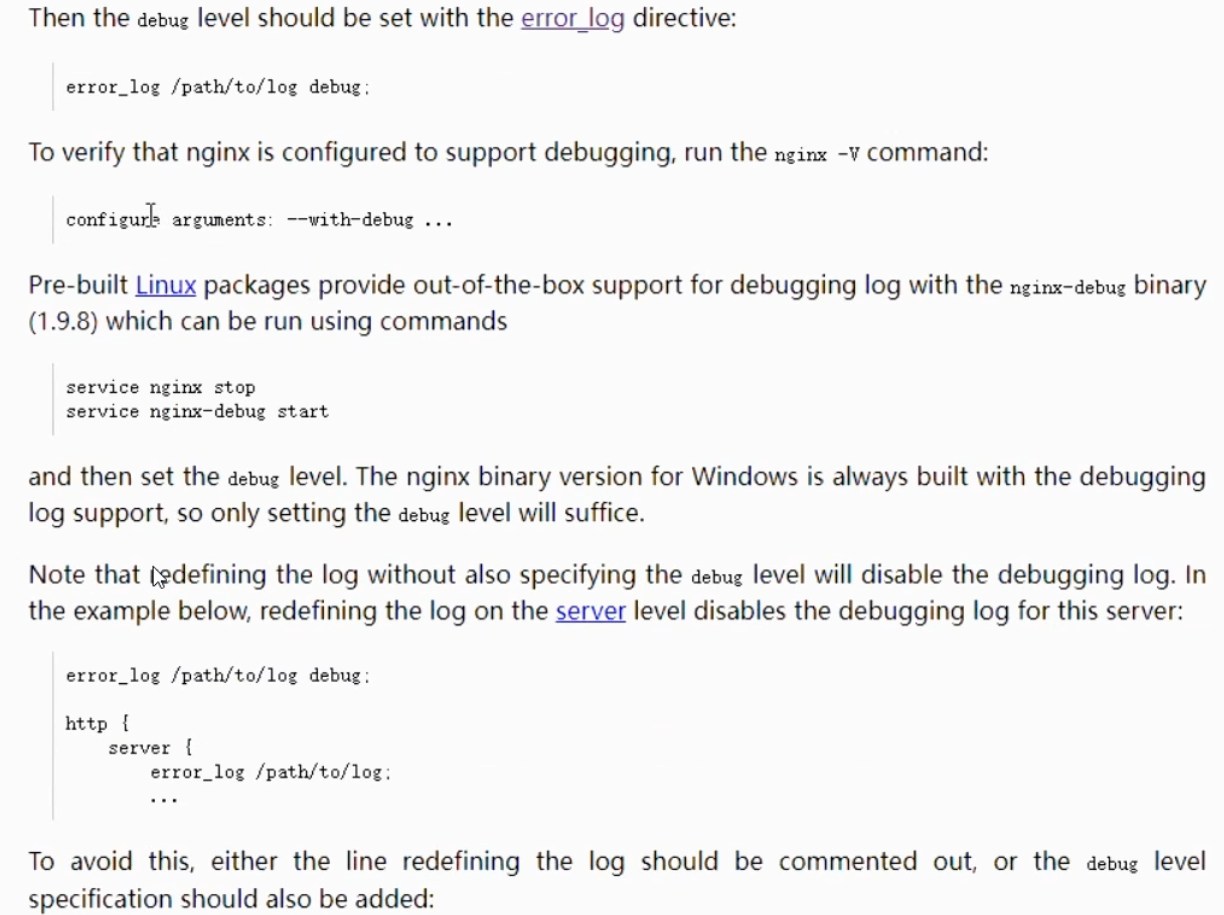
ngx错误日志error_log配置
ngx之error_log 日志配置格式: 常见的错误日志级别 错误日志可配置位置 关闭error_log配置 设置debug 日志级别的前提: ngx之error_log 日志配置格式: error_log 存放路径 日志级别 例: error_log /usr/local/log…...

1.11、自动化
自动化 一、java 手机自动化 首先new DesertCapabilities(这是一个类) setCapability – 设置信息 获取appium的驱动对象 new AppiumDriver – 本机IP地址:端口号/wd/hub,前面的设置值信息 driver.findElementById() – 通过id找位置 click() – 点击 &…...
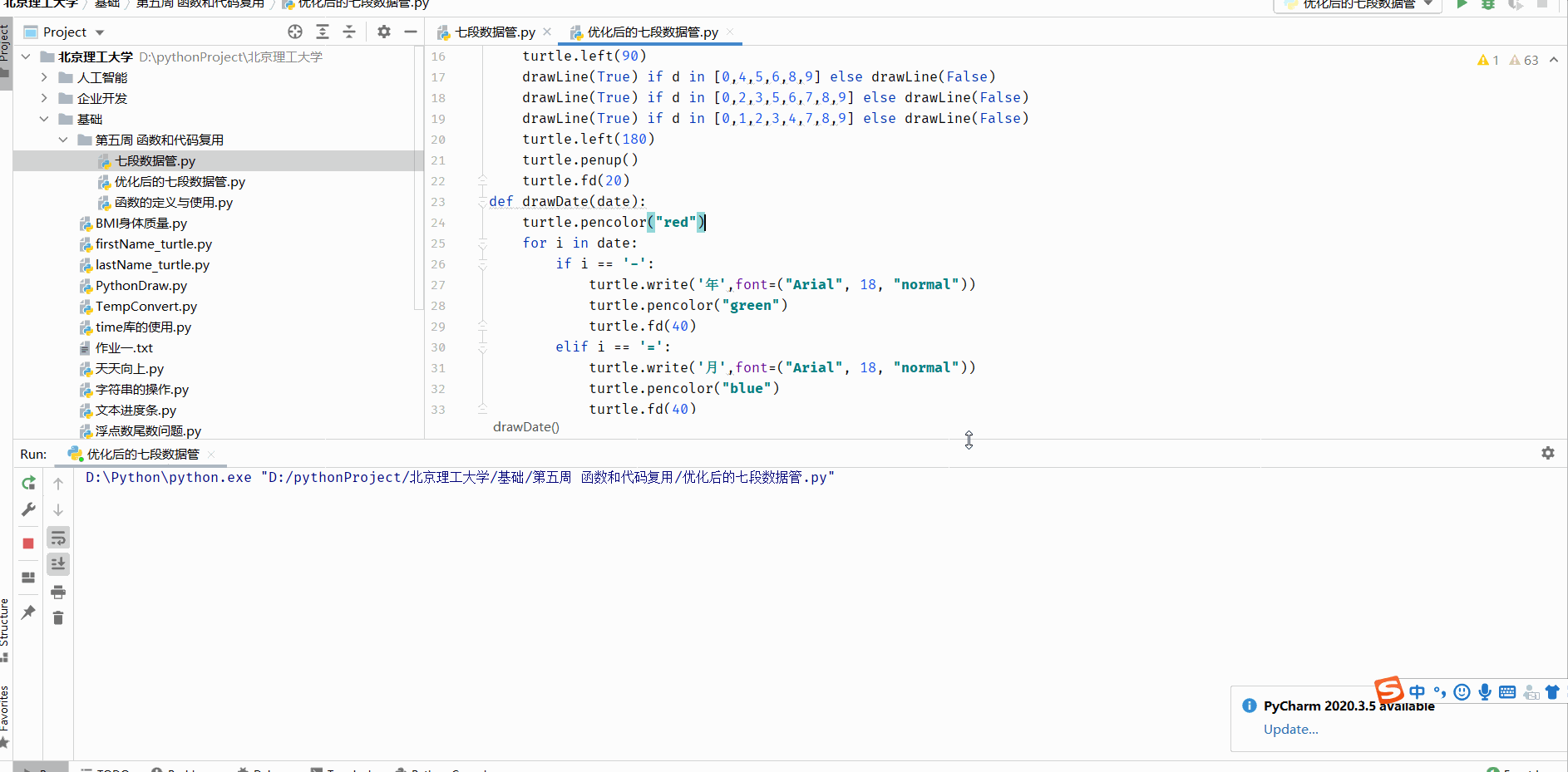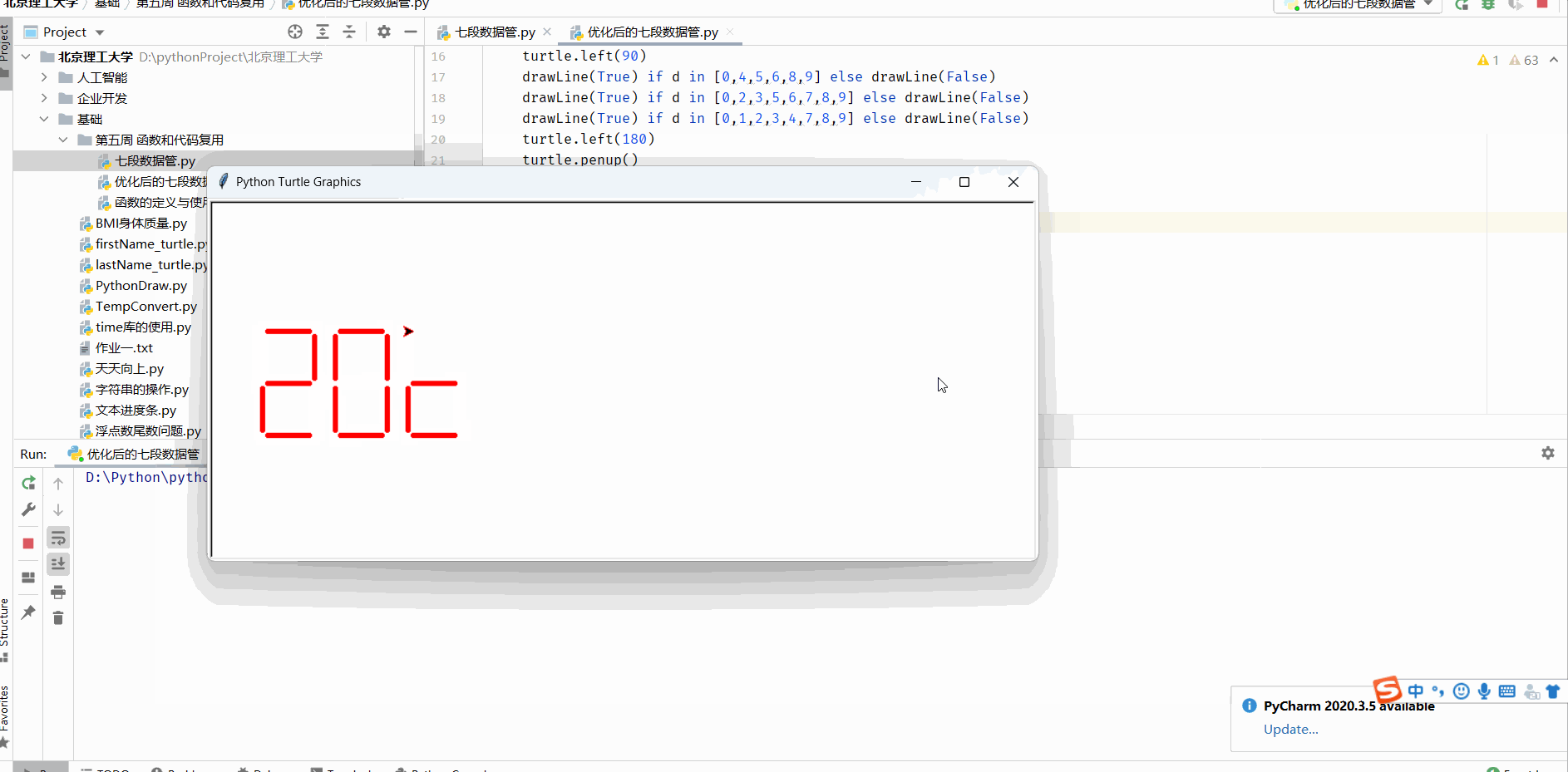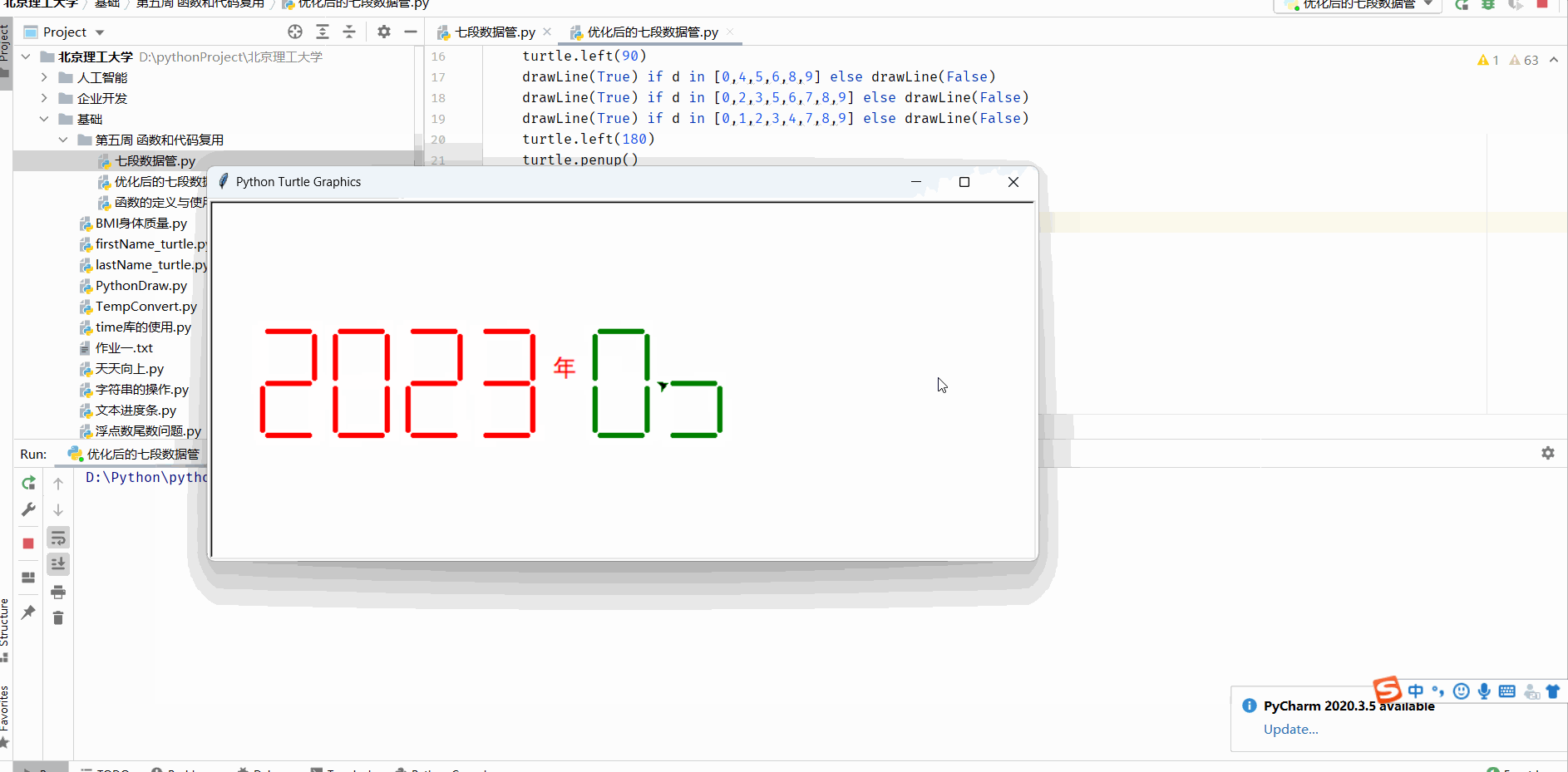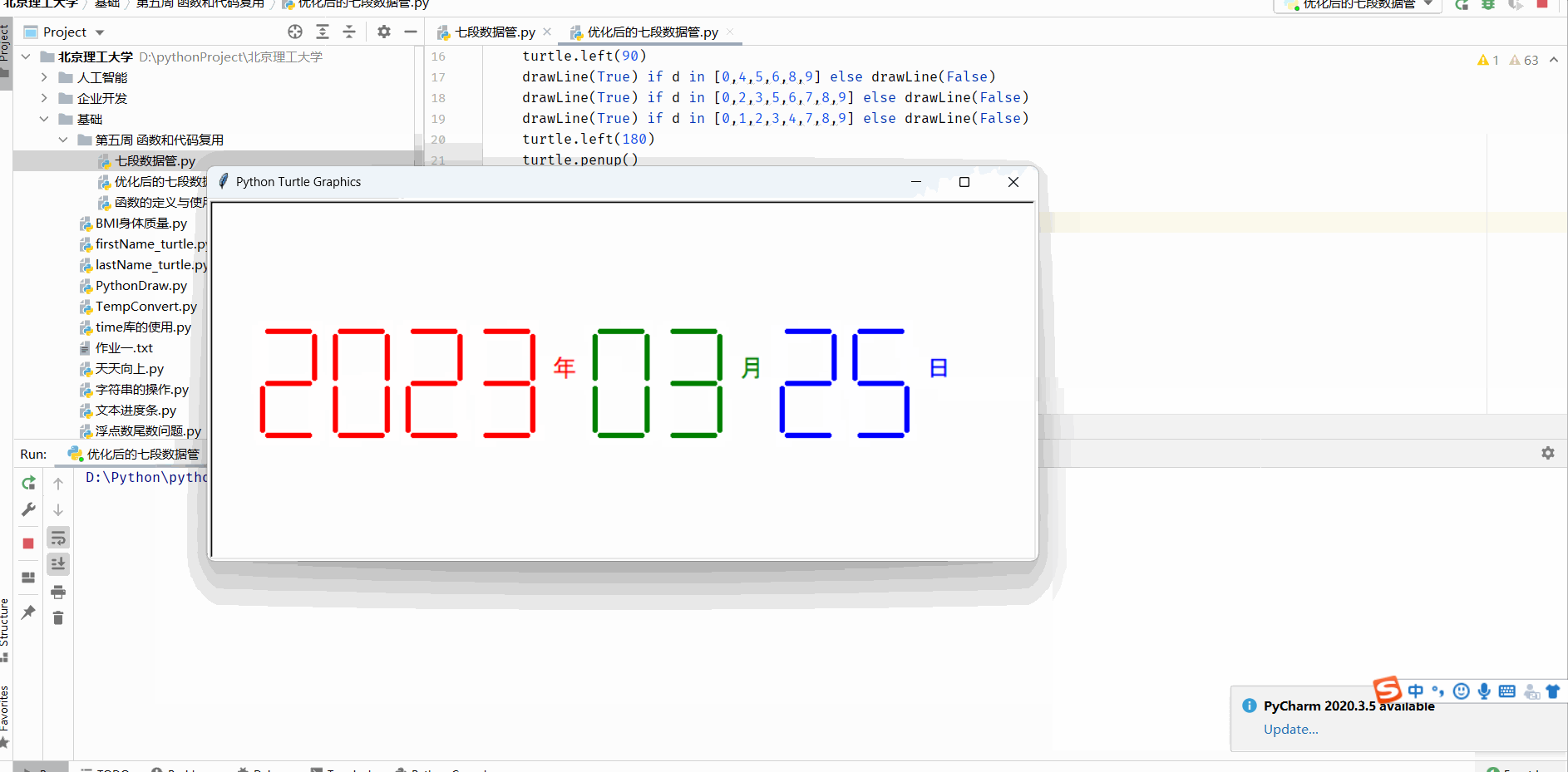
函数的定义与使用及七段数码管绘制
函数的定义 函数是一段代码的表示 函数是一段具有特定功能的、可重用的语句组 函数是一种功能的抽象,一般函数表达特定功能 两个作用:降低编程难度 和 代码复用 求一个阶乘 fact就是 函数名 n就是参数 return就是输出部分即返回值 而函数的调用就是…...

怎么压缩pdf文件大小?pdf文件太大如何压缩?
喜爱看小说的小伙伴们都会在网上下载很多的pdf格式电子书以方便随时阅览,但是pdf的电子书一般都过于的冗长,下载后的储存也是一个问题,怎么pdf压缩大小呢?可以试试今天介绍的这款pdf在线压缩工具来进行pdf压缩(https:/…...

阿里云Linux服务器登录名ecs-user和root选择问题
阿里云服务器Linux系统登录名可以选择root或ecs-user,root具有操作系统的最高权限,但是root会导致的安全风险比较大,ecs-user比较安全,但是如果系统后续依赖root权限就会比较麻烦,从安全的角度,建议选择ecs…...
,挂载配置文件使应用的配置和运行的镜像解耦)
【云原生】 初体验阿里云Serverless应用引擎SAE(三),挂载配置文件使应用的配置和运行的镜像解耦
目录 一、前言二、SAE配置1、创建配置项2、配置SAE Nginx服务效果1、【云原生】 初体验阿里云Serverless应用引擎SAE(一),部署Nginx服务 2、【云原生】 初体验阿里云Serverless应用引擎SAE(二),前端Nginx静态文件持久化到对象存储OSS 本篇 3、【云原生】 初体验阿里云Se…...
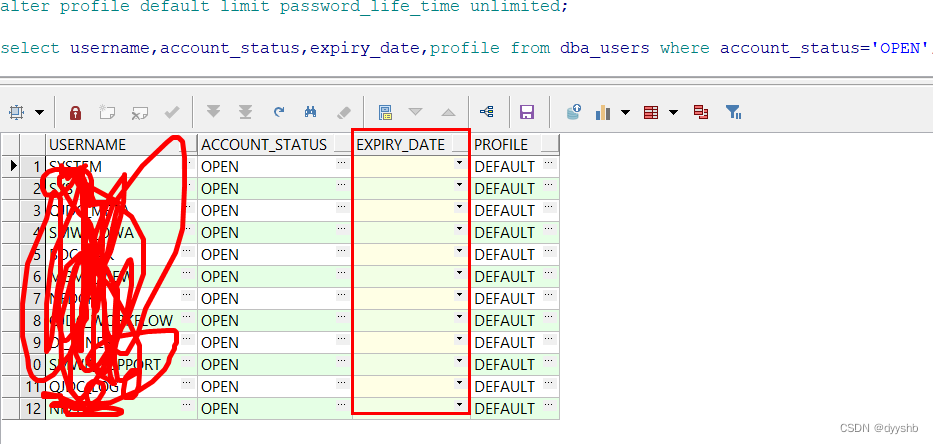
Oracle用户密码过期,修改永不过期
修改密码有效过期时间,可以通过以下四步设置,如果再第一步发现本身的密码过期时间为无限期的,那就请各位小伙伴绕过,如果发现不是无期限的,那么必须设置第四步,才会生效。 目录 第一步:查询密码…...
welearn 视听说1-4
词汇题(55道) 1. You should carefully think over_____ the manager said at the meeting. A. that B. which C. what D. whose 1.选C,考察宾语从句连接词,主句谓语动词think over后面缺宾语,后面的宾语从句谓语动…...

【git】将本地项目同步到远程
前提:git已经安装,并与账号完成密钥绑定 在github上创建一个新仓库 在项目文件夹下,右击选择git bash here ,打开一个终端对话框 git init (在项目目录下出现隐藏的.git文件夹,目的是把该项目文件夹变成git可管理…...
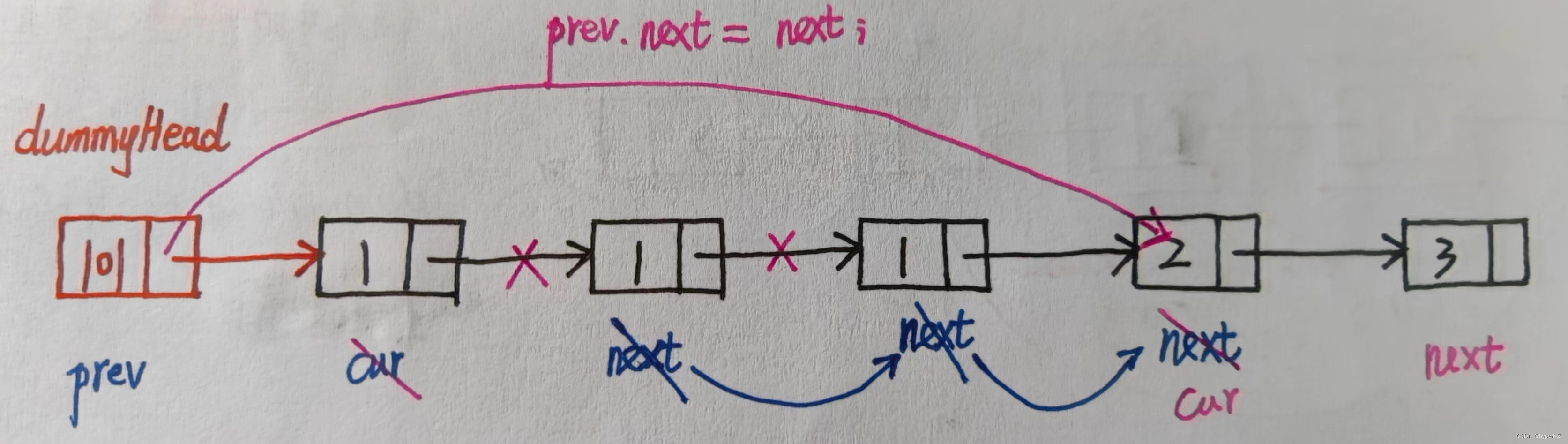
10-链表练习-LeetCode82删除排序链表中的重复元素II
题目 给定一个已排序的链表的头 head , 删除原始链表中所有重复数字的节点,只留下不同的数字 。返回已排序的链表 。 示例 1: 输入:head [1,2,3,3,4,4,5] 输出:[1,2,5] 示例 2: 输入:head …...

贯穿设计模式第五话--接口隔离原则
🥳🥳🥳 茫茫人海千千万万,感谢这一刻你看到了我的文章,感谢观赏,大家好呀,我是最爱吃鱼罐头,大家可以叫鱼罐头呦~🥳🥳🥳 从今天开始,将…...
)
C语言计算机二级/C语言期末考试 刷题(四)
在空闲时间整理了一些C语言计算机二级和C语言期末考试题库 整理不易,大家点赞收藏支持一下 祝大家计算机二级和期末考试都高分过 系列文章: C语言计算机二级/C语言期末考试 刷题(一) C语言计算机二级/C语言期末考试 刷题&#x…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

智能体革命:企业如何构建自主决策的AI代理?
OpenAI智能代理构建实用指南详解 随着大型语言模型(LLM)在推理、多模态理解和工具调用能力上的进步,智能代理(Agents)成为自动化领域的新突破。与传统软件仅帮助用户自动化流程不同,智能代理能够自主执行工…...
