【洛谷】P11036 【MX-X3-T3】「RiOI-4」GCD 与 LCM 问题 的题解
【洛谷】P11036 【MX-X3-T3】「RiOI-4」GCD 与 LCM 问题 的题解
题目传送门
题解
神奇构造题qaq
简化一下下题目,就是要求 a + b + c + d = gcd ( a , b ) + lcm ( c , d ) a + b + c +d = \gcd(a, b) + \operatorname{lcm}(c,d) a+b+c+d=gcd(a,b)+lcm(c,d)
分类讨论
- 考虑 a a a 为奇数的情况
令 b = a b = a b=a,则 gcd ( a , b ) = a \gcd(a,b)=a gcd(a,b)=a, lcm ( c , d ) = a + c + d \operatorname{lcm}(c,d)=a+c+d lcm(c,d)=a+c+d。如果令 d = 2 d=2 d=2, lcm ( c , 2 ) = 2 c \operatorname{lcm}(c,2)=2c lcm(c,2)=2c,显然 c = a + 2 c=a+2 c=a+2。构造 ( a , a , a + 2 , 2 ) (a,a,a+2,2) (a,a,a+2,2)。
- 考虑 a a a 为任意数的情况
令 b = a b=a b=a,打表观察得四元组 ( a , a , 2 lowbit ( a ) , a + 2 lowbit ( a ) ) (a,a,2\operatorname{lowbit}(a),a+2\operatorname{lowbit}(a)) (a,a,2lowbit(a),a+2lowbit(a))
具体实现可以直接枚举,时间复杂度 O ( log V ) O(\log V) O(logV),我用的是 lowbit ( a ) \operatorname{lowbit}(a) lowbit(a),比较保险,毕竟时间卡的挺死的,时间复杂度 O ( 1 ) O(1) O(1)。
代码
#include <bits/stdc++.h>
#define lowbit(x) x & (-x)
#define endl "\n"
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
namespace fastIO {inline int read() {register int x = 0, f = 1;register char c = getchar();while (c < '0' || c > '9') {if(c == '-') f = -1;c = getchar();}while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();return x * f;}inline void write(int x) {if(x < 0) putchar('-'), x = -x;if(x > 9) write(x / 10);putchar(x % 10 + '0');return;}
}
using namespace fastIO;
int a, c, t;
int main() {//freopen(".in","r",stdin);//freopen(".out","w",stdout);t = read(); for(int i = 1; i <= t; i ++) { a = read();c = (lowbit(a)) << 1; write(1), putchar(' '), write(c), putchar(' '), write(c + a), putchar('\n'); }return 0;
}
相关文章:

【洛谷】P11036 【MX-X3-T3】「RiOI-4」GCD 与 LCM 问题 的题解
【洛谷】P11036 【MX-X3-T3】「RiOI-4」GCD 与 LCM 问题 的题解 题目传送门 题解 神奇构造题qaq 简化一下下题目,就是要求 a b c d gcd ( a , b ) lcm ( c , d ) a b c d \gcd(a, b) \operatorname{lcm}(c,d) abcdgcd(a,b)lcm(c,d) 分类讨论 …...
——动态SQL)
MyBatis系统学习(三)——动态SQL
MyBatis 是一款优秀的持久层框架,它通过 XML 或注解方式将 SQL 语句与 Java 对象映射起来。动态 SQL 是 MyBatis 中非常强大的功能之一,能够根据不同的条件动态生成 SQL 语句。动态 SQL 通过各种标签来灵活生成 SQL,从而避免了在代码中拼接 S…...

get_property --Cmakelist之中
get_property 是 CMake 中用于获取目标、目录、变量或文件等属性的命令。它可以提取某个特定属性的值,以便在构建脚本的其他地方使用。 语法 get_property(<variable> <TYPE> <name> PROPERTY <property-name> [SET | DEFINED | BRIEF_DO…...
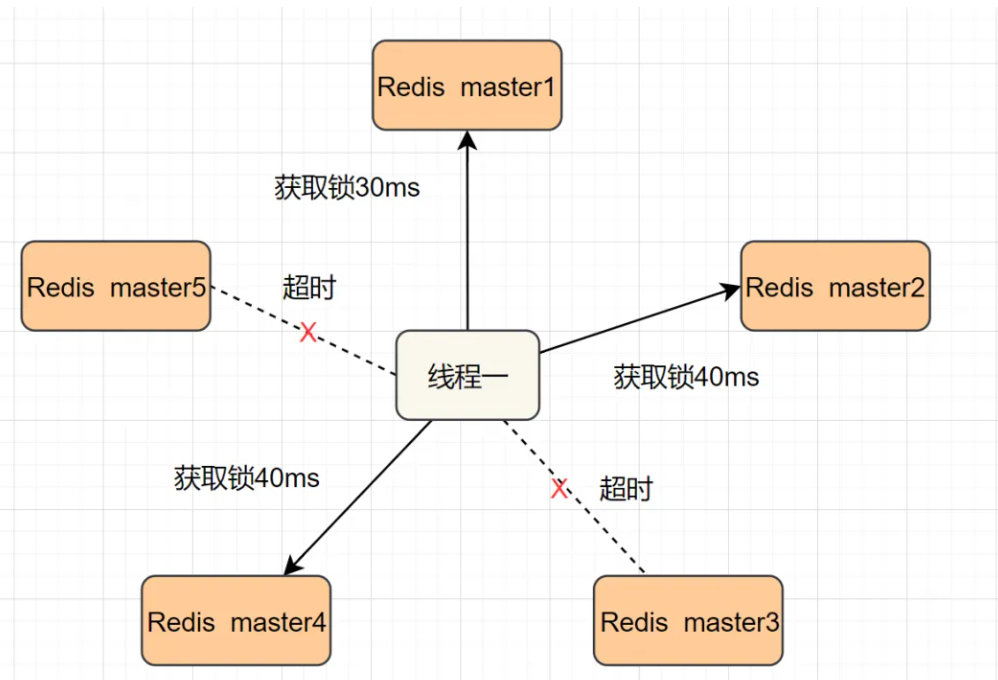
【Redis】Redis 典型应用 - 分布式锁原理与实现
目录 Redis 典型应⽤ - 分布式锁什么是分布式锁分布式锁的基础实现引⼊过期时间引⼊校验 id引⼊ lua引⼊ watch dog (看⻔狗)引⼊ Redlock 算法其他功能 Redis 典型应⽤ - 分布式锁 什么是分布式锁 在⼀个分布式的系统中, 也会涉及到多个节点访问同⼀个公共资源的…...

Pybind11的使用
目录 1. 引言1.1 Pybind11 简介1.2 为什么需要 Pybind11 2. 使用 Pybind11 进行 C 与 Python 交互2.1 基本用法2.2 编译与生成共享库2.2.1 在 Linux 下编译2.2.2 在 macOS 下编译2.2.3 编译选项详解 2.3 在 Python 中使用编译后的模块 3. 高级用法与注意事项3.1 绑定类和复杂数…...

鸿蒙-沉浸式pc端失效
咨询描述: 因PC北向窗口涉及沉浸式时,预计发生接口废弃导致不兼容变更,涉及接口setImmersiveModeEnabledState、setWindowLayoutFullSceen 如果应用支持沉浸式(窗口全屏且隐藏状态栏&标题栏&Dock栏)࿰…...

【资料分析】刷题日记1
第一套 第二个是相比2019年的增长率,错找为同比增长率 延申: 当出口和进口相比2019年的增长率相同时,可以用盐水解决 √ 一个假设分配(第二次是1.4取1)加法对比选项 基期倍数: 求A是B的多少倍&#x…...

nodejs+express+vue教辅课程辅助教学系统 43x2u前后端分离项目
目录 技术栈具体实现截图系统设计思路技术可行性nodejs类核心代码部分展示可行性论证研究方法解决的思路Express框架介绍源码获取/联系我 技术栈 该系统将采用B/S结构模式,开发软件有很多种可以用,本次开发用到的软件是vscode,用到的数据库是…...

96-javahashmap底层原理
HashMap是Java集合框架中的一个重要类,底层是基于哈希表实现的。哈希表是一种数据结构,可以通过哈希函数来提高查找、插入和删除操作的效率。 以下是HashMap底层实现的一些关键点: 哈希算法:HashMap使用哈希算法来计算键的哈希值…...

AI逻辑推理入门
参考数据鲸 (linklearner.com) 1. 跑通baseline 报名 申领大模型API 模型服务灵积-API-KEY管理 (aliyun.com) 跑通代码 在anaconda新建名为“LLM”的环境,并安装好相应包后,在jupyter notebook上运行baseline01.ipynb 2. 赛题解读 一般情况下,拿到一个赛题之后,我们需…...

力扣3014.输入单词需要的最少按键次数I
给你一个字符串 word,由 不同 小写英文字母组成。 电话键盘上的按键与 不同 小写英文字母集合相映射,可以通过按压按键来组成单词。例如,按键 2 对应 ["a","b","c"],我们需要按一次键来输入 "…...

【Git】远程仓库
本博客的环境是 Ubuntu/Linux 文章目录 集中式与分布式的区别远程仓库新建远程仓库克隆远程仓库向远程仓库推送从远程仓库拉取 配置Git忽略指定文件给命令配置别名 标签管理创建标签操作标签 多人协作本地分支与远程分支连接场景一场景二 集中式与分布式的区别 引荐自关于Git这…...

苹果手机铃声怎么设置自己的歌?3个方法自定义手机铃声
苹果手机内部的手机铃声库只有固定的几首铃声,且都是纯音乐,比较单调,并不是所有用户都喜欢这些铃声。那么,苹果手机铃声怎么设置自己的歌呢?小编这里有3个方法,可以教大家如何将手机铃声设置成自己喜欢的歌…...
828华为云征文|华为Flexus云服务器搭建Cloudreve私人网盘
一、华为云 Flexus X 实例:开启高效云服务新篇🌟 在云计算的广阔领域中,资源的灵活配置与卓越性能犹如璀璨星辰般闪耀。华为云 Flexus X 实例恰似一颗最为耀眼的新星,将云服务器技术推向了崭新的高度。 华为云 Flexus X 实例基于…...

【AI学习】AI绘画发展简史
无意中读了一篇发表自2022年的文章,《AI绘画何以突飞猛进? 从历史到技术突破, 一文读懂火爆的AI绘画发展史》,写的比较有意思,科普了好多我原来不知道的历史。 简单提炼一下,做个笔记。 AI绘画重要事件 2012年 Google两位大名…...

使用LangChain创建简单的语言模型应用程序【快速入门指南】
## 引言在这篇文章中,我们将展示如何使用LangChain构建一个简单的语言模型(LLM)应用程序。这个应用程序的功能是将文本从英语翻译成其他语言。尽管应用程序的逻辑相对简单,但它能够帮助我们学习如何使用LangChain进行更多复杂的功…...
嵌入式人工智能项目及人工智能应用项目——大合集列表查阅
本文的项目合集列表可能更新不及时(会及时更新),可查阅实时更新的链接如下。 嵌入式人工智能及人工智能应用项目合集实时更新链接如下: 阿齐嵌入式人工智能及人工智能应用项目合集 (kdocs.cn)https://www.kdocs.cn/l/cc97tuieys4…...

心觉:成功学就像一把刀,有什么作用关键在于使用者(一)
Hi,我是心觉,与你一起玩转潜意识、脑波音乐和吸引力法则,轻松掌控自己的人生! 挑战每日一省写作173/1000天 很多人觉得成功学是鸡汤,是没用的,甚至是骗人的 我先保持中立,不知道对不对 我们先…...
GAMES101(10节,几何)
Geometry implicit隐式几何表示: 函数f(x,y,z): 根据函数fn描述几何,遍历所有空间内 的点,如果带入xyz到函数f(x,y,z)结果0那就绘制这个点 如果xyz求值结果>0表示在几何外,0在表面,<0在几何内 构造几何csg(…...

Android 中音频焦点的使用场景及示例
Android 中音频焦点的使用场景及代码示例 一、音频焦点简介 在 Android 系统中,音频焦点(Audio Focus)是一种机制,用于管理多个应用程序同时播放音频时的冲突。当一个应用程序请求音频焦点并获得它时,其他应用程序在…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...
