Java-数据结构-优先级队列(堆)-(一) (;´д`)ゞ
文本目录:
❄️一、优先级队列:
➷ 1、概念:
❄️二、优先级队列的模拟实现:
➷ 1、堆的概念:
➷ 2、堆的性质:
➷ 3、堆的创建:
▶ 向下调整:
➷ 4、堆的插入和删除:
▶ 堆的插入:
☞ 思路:
☞ 代码:
▶ 堆的删除:
☞ 思路:
☞ 代码:
➷ 5、堆的判空和判满:
➷ 6、堆的对顶数据:
➷ 7、堆的总代码:
❄️总结:
 ❄️一、优先级队列:
❄️一、优先级队列:
➷ 1、概念:
我们在前面是介绍过队列的,队列是一种先进先出的数据结构,但是在有些情况下呢,我们操作的数据有优先级,这时候,在我们出队列的时候呢,可能需要先出优先级高的先出队列,那么在这种情况下呢,我们的队列就是有些不合适了,比如呢,我们在 玩游戏的时候呢,来个电话,是不是手机先处理电话,之后再处理游戏去。
在这种情况下,数据结构提供了两种最基本的操作:一个事返回优先级最高的对象,另一个是添加新的对象。这种操作呢就是 优先级队列——Priority Queue
 ❄️二、优先级队列的模拟实现:
❄️二、优先级队列的模拟实现:
在 JDK1.8 中呢,我们的 Priority Queue 的底层使用了堆的数据结构,而对于 堆呢就是在 完全二叉树 的基础上进行一些调整的。
➷ 1、堆的概念:
如果有一个关键码的集合 K = {K0,K1,K2,.......,Kn - 1},把它的所有数据都按照 完全二叉树的顺序存储方式存储 在一个一维数组中,并且满足:
Ki <= K2i + 1 且 Ki <= K2i + 2 (Ki >= K2i + 1 且 Ki >= K2i + 2) i = 0,1,2,3,4,5.......,
则称为 小堆(大堆)。
在这里我们 将根节点最大的堆称为 最大堆 或者 大根堆
将根节点最小的堆称为 最小堆 或者 小根堆
➷ 2、堆的性质:
• 堆中某个节点的值总是 不大于 或者 不小于 其父节点的值。
• 堆是一颗完全二叉树。
我们来看看 大根堆 和 小根堆 的逻辑结构和存储结构:

我们的存储方式是采用 层序存储 的 规则来进行存储到数组中。这样就非常的高效了。
我们要注意如果不是 完全二叉树 的情况下呢,我们的不能使用 层序遍历的存储规则,这样会浪费空间,所以如果不是完全二叉树不能这样做。
➷ 3、堆的创建:
我们在创建堆之前呢,我们先来做一些准备工作,我们要注意我们的堆的底层使用的是数组进行实现的。
我们将这些数据变成 大根堆 或者 小根堆 但是呢,我们要如何才能创建 大根堆 或者 小根堆 呢?
在创建 大根堆 或者 小根堆 之前呢,我们先把这个数组的值呢变成 完全二叉树 来看看:

我们红色的字体就是我们的数组的下标。这个就是我们这组数据的 完全二叉树 的逻辑结构。
那么我们要如何创建堆呢?这里呢我们要了解到一个知识点——向下调整。
▶ 向下调整:
我们这里是 从最后一颗子树进行调整,找到最后一颗子树的根节点,再比较这个根节点的左右节点谁大,我们把根节点和这个最大值进行调整,这样循环调整每一颗子树。这样就可以调整成大根堆。
这里呢,我们直接看图来理解这个问题:
这就是我们的大根堆的调整方法从 完全二叉树 调整。
这里我们需要一些必须要求的东西:
1、首先要找到最后一颗子树的位置,也就是最后一颗子树的根节点。
这里我们使用一个公式:(数组的长度 - 1 - 1)/ 2 就是我们的最后一颗子树的根节点。我们使用 parent 标记这个节点。
2、我们如何找到我们的下一颗子树的根节点位置?
这个就比较简单了,我们直接 parent-- 就可以了。直至我们的 parent 下标 >= 0 即可比如:
3、我们要知道我们的子树的 左子树 ,为什么是左子树呢?因为是由 完全二叉树 调整而来,如果 没有左子树就没有右子树,所以只需要找到左子树即可。
那么怎样去找呢?这里也有公式:child = parent * 2 + 1 ,就是我们左子树。但是这个呢我们还要找其左右子树最大的值,不是直接对child进行交换的。并且要注意我们的 child 要 小于 有效的数组长度。
4、我们怎样知道我们的调整结束了?
这里我们不能调整一次就结束,这里的结束条件就是,当我们的 左子树这个节点的下标比有效数组长度长的时候就是结束的时候了。
每次我们要对 child 和 parent 进行调整。parent = child child = parent * 2 + 1
我们来演示一变看看如何进行的:
这就是我们的 向下调整 成 大根堆 的操作。来看看这个 向下调整 的代码:
/**** @param parent 每颗子树调整时候的起始位置* @param usedSize 用来判断 每颗子树什么时候结束的*/private void shiftDown(int parent,int usedSize) {int child = parent * 2 + 1;//parent根节点的左子树的节点while (child < usedSize) {//判断有没有右子树,如果有就把 child 设置为最大的值的下标if (child + 1 < usedSize && elem[child + 1] > elem[child]) {//右子树比左子树大把 child + 1,就是右子树child += 1;}if (elem[parent] < elem[child]) {//进行交换swap(elem,child,parent);//调整完,把 parent 和 child 进行调整位置parent = child;child = parent * 2 + 1;}else {//这是 parent下标的值大于child,跳出break;}}}private void swap(int[] elem,int i,int j) {int tmp = elem[i];elem[i] = elem[j];elem[j] = tmp;}这个呢就是我们的 向下调整 的 创建大根堆,对于我们的要是 创建 小根堆 的话就是把其小的数值进行调整就可以了,就是反过来进行调整。
我们这个时候来看看对于堆的创建,了解到 向下调整 之后呢,就是非常的容易了,我们呢就是把每一个 parent 进行 向下调整,这里就用到循环遍历就可以了。
我们来看代码:
//堆的创建public void createHeap() {for (int parent = (this.usedSize - 1 - 1) / 2; parent >= 0 ; parent--) {shiftDown(parent,this.usedSize);}}Ok啊,这样我们的 大根堆的创建 就创建完成了。
➷ 4、堆的插入和删除:
▶ 堆的插入:
☞ 思路:
对于我们的堆的插入的操做呢,我们的插入一定是在最后一个位置插入的,这个位置,我们一定是知道的,就是我们的 usedSize 这个下标的位置插入数据。我们就可以根据这个位置求出其插入的值的根节点的位置。
我们来看图来理解:

这个 90 就是我们新插入的值,我们再对其进行 向上调整,我们是知道插入值的下标,就可以计算到根节点的下标,就可以进行 向上调整了 。 
再对其进行向上调整就可以了。 
这里我们也要注意当我们的数组使用满了后,我们就需要扩容了。
这个就是插入的操作了。我们来看看代码是如何编写的:
☞ 代码:
//堆的插入public void offer(int val) {if (usedSize == elem.length) {//满了。2倍扩容this.elem = Arrays.copyOf(this.elem, 2 * this.elem.length);}//插入操作this.elem[usedSize] = val;//这个时候 usedSize 位置就是我们的子树的坐标位置shiftUp(usedSize);this.usedSize++;}private void shiftUp(int child) {int parent = (child - 1) / 2;while (parent >= 0) {//进行向上调整if (this.elem[parent] < this.elem[child]) {//交换swap(elem,child,parent);//parent 和 child 调整位置child = parent;parent = (child - 1) / 2;}else {break;}}}OK,这个呢就是我们的插入操作的代码了之后我们来看看删除操作是如何做到的。
▶ 堆的删除:
☞ 思路:
这个删除操作还是很简单的,我们需要删除优先级高的数据,所以我们删除的就是 0 下标的值
我们呢有三个步骤:
1、把堆的 0 下标的数据 和 usedSize - 1 这个下标的数据进行交换,就是第一个数据和最后一个 数据进行交换。
2、我们把有效数组长度减一。
3、我们就是 0 这个下标不是大根堆的结构,所以我们对 0 这个下标进行 向下调整 操作。
这个呢就是我们删除的思路了,我们接下来看看其代码:
☞ 代码:
//堆的删除操作public int poll() {//删除优先级最高的就是0下标的值,有三个步骤://1、把堆的第一个数据和最后一个数据进行交换//2、把有效数据长度进行减1//3、把 0 下标的值进行向下调整if (usedSize == 0) {//堆为空,结束return -1;}int val = elem[0];//1、swap(elem,0,usedSize - 1);//2、usedSize--;//3、shiftDown(0,usedSize);return val;}➷ 5、堆的判空和判满:
这两个操作就非常的简单了,我们直接来看代码:
//判空public boolean isEmpty() {return usedSize == 0;}//判满public boolean isFull() {return usedSize == this.elem.length;}➷ 6、堆的对顶数据:
这个同样非常的简单,我们直接返回下标为 0 的值就可以了。
//返回堆顶的数据public int peek() {if (isEmpty()) {return -1;}return this.elem[0];}这样呢我们所有的基本操作就都完成了,我们来看一下总代码:
➷ 7、堆的总代码:
import java.util.Arrays;public class TestHeap {public int[] elem;public int usedSize;public TestHeap() {//初始话this.elem = new int[10];}public void initElem(int[] array) {//把elem里的值设置为我们输入的值for (int i = 0; i < array.length; i++) {elem[i] = array[i];}}/*** 建堆的时间复杂度为O(N)。* 大根堆* @param parent 每颗子树调整时候的起始位置* @param usedSize 用来判断 每颗子树什么时候结束的*/private void shiftDown(int parent,int usedSize) {int child = parent * 2 + 1;//parent根节点的左子树的节点while (child < usedSize) {//判断有没有右子树,如果有就把 child 设置为最大的值的下标if (child + 1 < usedSize && elem[child + 1] > elem[child]) {//右子树比左子树大把 child + 1,就是右子树child += 1;}if (elem[parent] < elem[child]) {//进行交换swap(elem,child,parent);//调整完,把 parent 和 child 进行调整位置parent = child;child = parent * 2 + 1;}else {//这是 parent下标的值大于child,跳出break;}}}private void swap(int[] elem,int i,int j) {int tmp = elem[i];elem[i] = elem[j];elem[j] = tmp;}//大根堆的创建public void createHeap() {for (int parent = (this.usedSize - 1 - 1) / 2; parent >= 0 ; parent--) {shiftDown(parent,this.usedSize);}}//堆的插入public void offer(int val) {if (isFull()) {//满了。2倍扩容this.elem = Arrays.copyOf(this.elem, 2 * this.elem.length);}//插入操作this.elem[usedSize] = val;//这个时候 usedSize 位置就是我们的子树的坐标位置shiftUp(usedSize);this.usedSize++;}private void shiftUp(int child) {int parent = (child - 1) / 2;while (parent >= 0) {//进行向上调整if (this.elem[parent] < this.elem[child]) {//交换swap(elem,child,parent);//parent 和 child 调整位置child = parent;parent = (child - 1) / 2;}else {break;}}}//堆的删除操作public int poll() {//删除优先级最高的就是0下标的值,有三个步骤://1、把堆的第一个数据和最后一个数据进行交换//2、把有效数据长度进行减1//3、把 0 下标的值进行向下调整if (isEmpty()) {//堆为空,结束return -1;}int val = elem[0];//1、swap(elem,0,usedSize - 1);//2、usedSize--;//3、shiftDown(0,usedSize);return val;}//返回堆顶的数据public int peek() {if (isEmpty()) {return -1;}return this.elem[0];}//判空public boolean isEmpty() {return usedSize == 0;}//判满public boolean isFull() {return usedSize == this.elem.length;}
}
 ❄️总结:
❄️总结:
OK,这篇博客呢就到这里就结束了,这篇博客我们介绍的是 优先级队列 的底层操作代码,下一篇博客我们来看看 Java 自带的 优先级队列吧~~并且还有一些关于我们的优先级队列的习题,敬请期待吧!!!拜拜·~~~

相关文章:

Java-数据结构-优先级队列(堆)-(一) (;´д`)ゞ
文本目录: ❄️一、优先级队列: ➷ 1、概念: ❄️二、优先级队列的模拟实现: ➷ 1、堆的概念: ➷ 2、堆的性质: ➷ 3、堆的创建: ▶ 向下调整: ➷ 4、堆的插入和删除: …...

工厂模式(二):工厂方法模式
一、概念 工厂方法模式(Factory Method),定义一个用于创建对象的接口,让子类决定实例化哪一个类。工厂方法使一个类的实例化延迟到其子类。从而使得系统更加灵活。客户端可以通过调用工厂方法来创建所需的产品,而不必…...

【洛谷】P11036 【MX-X3-T3】「RiOI-4」GCD 与 LCM 问题 的题解
【洛谷】P11036 【MX-X3-T3】「RiOI-4」GCD 与 LCM 问题 的题解 题目传送门 题解 神奇构造题qaq 简化一下下题目,就是要求 a b c d gcd ( a , b ) lcm ( c , d ) a b c d \gcd(a, b) \operatorname{lcm}(c,d) abcdgcd(a,b)lcm(c,d) 分类讨论 …...
——动态SQL)
MyBatis系统学习(三)——动态SQL
MyBatis 是一款优秀的持久层框架,它通过 XML 或注解方式将 SQL 语句与 Java 对象映射起来。动态 SQL 是 MyBatis 中非常强大的功能之一,能够根据不同的条件动态生成 SQL 语句。动态 SQL 通过各种标签来灵活生成 SQL,从而避免了在代码中拼接 S…...

get_property --Cmakelist之中
get_property 是 CMake 中用于获取目标、目录、变量或文件等属性的命令。它可以提取某个特定属性的值,以便在构建脚本的其他地方使用。 语法 get_property(<variable> <TYPE> <name> PROPERTY <property-name> [SET | DEFINED | BRIEF_DO…...
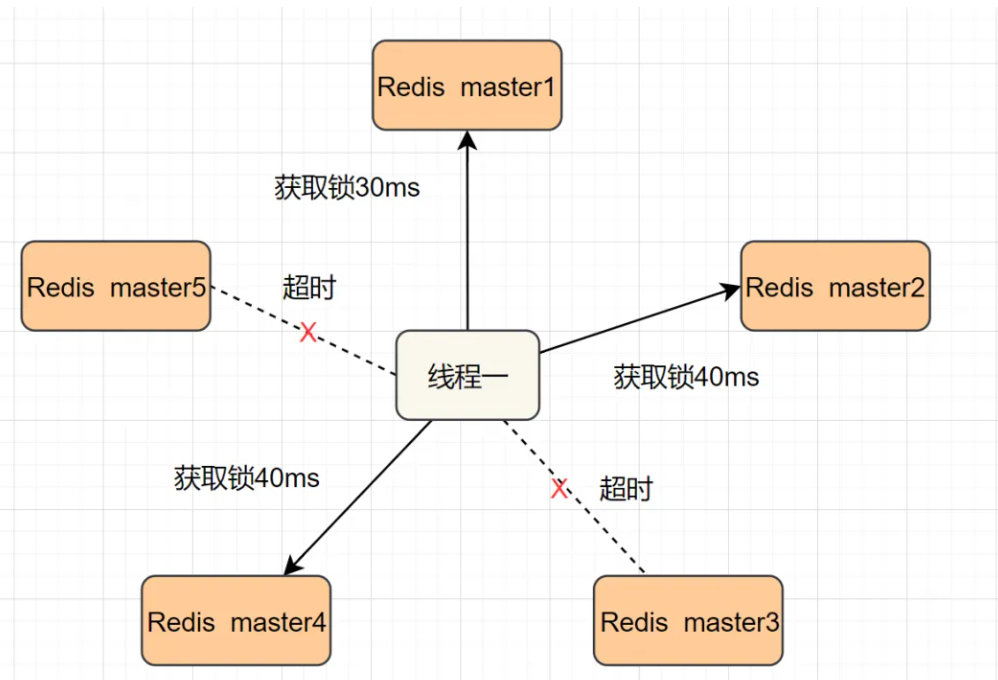
【Redis】Redis 典型应用 - 分布式锁原理与实现
目录 Redis 典型应⽤ - 分布式锁什么是分布式锁分布式锁的基础实现引⼊过期时间引⼊校验 id引⼊ lua引⼊ watch dog (看⻔狗)引⼊ Redlock 算法其他功能 Redis 典型应⽤ - 分布式锁 什么是分布式锁 在⼀个分布式的系统中, 也会涉及到多个节点访问同⼀个公共资源的…...

Pybind11的使用
目录 1. 引言1.1 Pybind11 简介1.2 为什么需要 Pybind11 2. 使用 Pybind11 进行 C 与 Python 交互2.1 基本用法2.2 编译与生成共享库2.2.1 在 Linux 下编译2.2.2 在 macOS 下编译2.2.3 编译选项详解 2.3 在 Python 中使用编译后的模块 3. 高级用法与注意事项3.1 绑定类和复杂数…...

鸿蒙-沉浸式pc端失效
咨询描述: 因PC北向窗口涉及沉浸式时,预计发生接口废弃导致不兼容变更,涉及接口setImmersiveModeEnabledState、setWindowLayoutFullSceen 如果应用支持沉浸式(窗口全屏且隐藏状态栏&标题栏&Dock栏)࿰…...

【资料分析】刷题日记1
第一套 第二个是相比2019年的增长率,错找为同比增长率 延申: 当出口和进口相比2019年的增长率相同时,可以用盐水解决 √ 一个假设分配(第二次是1.4取1)加法对比选项 基期倍数: 求A是B的多少倍&#x…...

nodejs+express+vue教辅课程辅助教学系统 43x2u前后端分离项目
目录 技术栈具体实现截图系统设计思路技术可行性nodejs类核心代码部分展示可行性论证研究方法解决的思路Express框架介绍源码获取/联系我 技术栈 该系统将采用B/S结构模式,开发软件有很多种可以用,本次开发用到的软件是vscode,用到的数据库是…...

96-javahashmap底层原理
HashMap是Java集合框架中的一个重要类,底层是基于哈希表实现的。哈希表是一种数据结构,可以通过哈希函数来提高查找、插入和删除操作的效率。 以下是HashMap底层实现的一些关键点: 哈希算法:HashMap使用哈希算法来计算键的哈希值…...

AI逻辑推理入门
参考数据鲸 (linklearner.com) 1. 跑通baseline 报名 申领大模型API 模型服务灵积-API-KEY管理 (aliyun.com) 跑通代码 在anaconda新建名为“LLM”的环境,并安装好相应包后,在jupyter notebook上运行baseline01.ipynb 2. 赛题解读 一般情况下,拿到一个赛题之后,我们需…...

力扣3014.输入单词需要的最少按键次数I
给你一个字符串 word,由 不同 小写英文字母组成。 电话键盘上的按键与 不同 小写英文字母集合相映射,可以通过按压按键来组成单词。例如,按键 2 对应 ["a","b","c"],我们需要按一次键来输入 "…...

【Git】远程仓库
本博客的环境是 Ubuntu/Linux 文章目录 集中式与分布式的区别远程仓库新建远程仓库克隆远程仓库向远程仓库推送从远程仓库拉取 配置Git忽略指定文件给命令配置别名 标签管理创建标签操作标签 多人协作本地分支与远程分支连接场景一场景二 集中式与分布式的区别 引荐自关于Git这…...

苹果手机铃声怎么设置自己的歌?3个方法自定义手机铃声
苹果手机内部的手机铃声库只有固定的几首铃声,且都是纯音乐,比较单调,并不是所有用户都喜欢这些铃声。那么,苹果手机铃声怎么设置自己的歌呢?小编这里有3个方法,可以教大家如何将手机铃声设置成自己喜欢的歌…...
828华为云征文|华为Flexus云服务器搭建Cloudreve私人网盘
一、华为云 Flexus X 实例:开启高效云服务新篇🌟 在云计算的广阔领域中,资源的灵活配置与卓越性能犹如璀璨星辰般闪耀。华为云 Flexus X 实例恰似一颗最为耀眼的新星,将云服务器技术推向了崭新的高度。 华为云 Flexus X 实例基于…...

【AI学习】AI绘画发展简史
无意中读了一篇发表自2022年的文章,《AI绘画何以突飞猛进? 从历史到技术突破, 一文读懂火爆的AI绘画发展史》,写的比较有意思,科普了好多我原来不知道的历史。 简单提炼一下,做个笔记。 AI绘画重要事件 2012年 Google两位大名…...

使用LangChain创建简单的语言模型应用程序【快速入门指南】
## 引言在这篇文章中,我们将展示如何使用LangChain构建一个简单的语言模型(LLM)应用程序。这个应用程序的功能是将文本从英语翻译成其他语言。尽管应用程序的逻辑相对简单,但它能够帮助我们学习如何使用LangChain进行更多复杂的功…...
嵌入式人工智能项目及人工智能应用项目——大合集列表查阅
本文的项目合集列表可能更新不及时(会及时更新),可查阅实时更新的链接如下。 嵌入式人工智能及人工智能应用项目合集实时更新链接如下: 阿齐嵌入式人工智能及人工智能应用项目合集 (kdocs.cn)https://www.kdocs.cn/l/cc97tuieys4…...

心觉:成功学就像一把刀,有什么作用关键在于使用者(一)
Hi,我是心觉,与你一起玩转潜意识、脑波音乐和吸引力法则,轻松掌控自己的人生! 挑战每日一省写作173/1000天 很多人觉得成功学是鸡汤,是没用的,甚至是骗人的 我先保持中立,不知道对不对 我们先…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
