【隐私计算篇】中国剩余定理解释以及Paillier解密加速应用
1. 背景介绍
本篇主要关注中国剩余定理的原理以及在paillier同态加密系统中的应用。在很多工作中,都可以看到中国剩余定理的影子,特别是同态加密提升计算效率的优化工作中,将paillier与中国剩余定理进行结合,能够实现在加密状态下进行高效计算。
2. Paillier加密系统
【1,2,3】描述了paillier加密系统的原理。这里做简单的描述。Paillier加密算法是一种同态加密算法,支持加法同态运算。该算法的安全性基于大整数的分解困难问题,具体的加密和解密过程涉及模数 上的运算,计算复杂度较高。
2.1 Paillier密钥生成
- 选择两个大质数 p 和 q,计算
。
- 公钥为 N 和 g(通常选择 g = N + 1)。
- 私钥为
和
,其中:
(即 p-1 和 q-1 的最小公倍数)。
,其中
。
2.2 加密和解密
- 加密:给定明文 m,选择随机数 r,计算密文
。
- 解密:给定密文 c,解密过程为:
这里的模
运算会涉及非常大的数,计算较为耗时。
3. 中国剩余定理(CRT)
3.1 算法描述
中国剩余定理(Chinese Remainder Theorem, CRT)【4,5】是数论中的一个经典定理,用来解决模数互素时同余方程组的求解问题。它最早起源于中国古代数学家孙子在《孙子算经》中的研究。
设 是两两互素的整数,也就是说,对于
,有
。给定同余方程组:
其中 是给定的整数,则该方程组有唯一解 x (模
),并且解的形式为:
定理的意义:
- 解的存在性:如果模数
互素,则方程组总有解。
- 解的唯一性:在模
意义下,解是唯一的。
解法步骤:
- 计算总模数:计算模数的乘积
。
- 计算每个模的辅助量:对于每个 i,计算
,即其他模数的乘积。
- 计算模逆元:对于每个 i,找到
模
的逆元
,即满足
的整数
。
- 求解 x:解的形式为:
其中
是同余方程组中的常数项,
是步骤 2 中的值,
是步骤 3 中的模逆元。
此外,也关注到【6】对于中国剩余定理的解释比较清晰,这里也贴一下,以便参考学习。

3.2 模 n 同余概念
模 n 同余是数论中的一个概念,用来表示两个整数在被同一个整数 n 除时得到相同的余数。具体来说,模 n 同余是指两个整数 a 和 b,如果 a 和 b 被 n 除后余数相同,那么我们说 a 和 b 在模 n 意义下同余,记作:
这表示 a - b 能被 n 整除,即存在某个整数 k 使得:
其中:
-
a 和 b 是两个整数。
-
n 是模数(或称模量),是一个正整数。
-
表示当 a 和 b 都被 n 除后,余数相同,或者说 a - b 是 n 的倍数。
3.3 中国剩余定理应用问题说明
中国剩余定理的原问题如下:
有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?
问题的意思是找一个数 x,满足以下三个同余条件:
我们要解这个系统,找到 x 满足所有条件。
解法步骤:
从第一个和第二个条件开始:
设
,代入
:
即:
我们需要解这个同余方程。找到
即 3 在模 5 下的逆元。通过尝试:
所以
。即
,代入
:
考虑第三个条件
: 现在有
,代入
:
即:
由于
,所以:
考虑
,所以这个方程化简为:
即
。代入
:
得出最终结果: 所以,满足条件的数 x 可以表示为:
其中 n 是任意整数。因此,最小的正整数解是 x = 23。
所以这个物的数是 23。
4. Paillier引入中国剩余定理
4.1 思路介绍
中国剩余定理与Paillier加密算法结合可以有效提升计算效率,尤其是在大数模运算的场景中。通过利用中国剩余定理的性质,将涉及大整数的计算拆分为两个较小模数空间中的并行计算,从而加快整体的运算速度。这种结合方式在Paillier加密算法中的典型应用是加速解密过程。
具体地,中国剩余定理用于将大整数的计算分解为在较小整数模数下的并行计算。对于给定的两个模数 p 和 q,可以将模 下的计算转化为模 p 和模 q 下的两个独立计算。
设 ,对于任何整数 x,有:
通过在较小模数空间中分别计算 和
,可以加快运算速度。
Paillier算法中的解密操作主要依赖于模 的运算,而
是一个非常大的数。通过中国剩余定理,可以将这些大模数运算分解为在较小模数
和
下的并行计算,从而加速解密过程。
4.2 处理步骤
-
分解模数空间:
利用中国剩余定理,将模下的运算分解为模
和模
的运算。
-
并行计算:
在解密过程中,密文 c 的解密需要计算。通过中国剩余定理,可以将这一操作分解为:
,
其中
,
。
-
重构结果:
利用中国剩余定理的逆过程,将模和模
下的结果
和
通过CRT重构为最终的明文
:
这一步通过快速计算结合模 p 和 q 的结果,得到最终的解密结果。
- 在原始论文【2】中,其实也列出了相应的说明:

通过将模 下的计算分解为较小的模
和模
下的计算,可以显著减少大整数运算的复杂度。由于
和
远小于 N^2,解密速度可以得到明显提升。
4.3 推理依赖的定理
这里根据哥大的材料【7】,列出paillier系统相关的定理,有兴趣可以看下定理的证明过程。 
5. 参考材料
【1】A Restrained Paillier Cryptosystemand Its Applications for Access Control of Common Secret
【2】Public-Key Cryptosystems Based on Composite Degree Residuosity Classes
【3】Paillier同态加密算法
【4】中国剩余定理
【5】The Chinese Remainder Theorem
【6】密码学-05-中国剩余定理
【7】Facts Related to Paillier Encryption
相关文章:

【隐私计算篇】中国剩余定理解释以及Paillier解密加速应用
1. 背景介绍 本篇主要关注中国剩余定理的原理以及在paillier同态加密系统中的应用。在很多工作中,都可以看到中国剩余定理的影子,特别是同态加密提升计算效率的优化工作中,将paillier与中国剩余定理进行结合,能够实现在加密状态下…...

保护您的隐私:隐藏 IP 地址的重要性
在当今的数字时代,我们的在线隐私和安全变得比以往任何时候都更加重要。浏览互联网时保护自己的一种方法是隐藏您的 IP 地址。 但是为什么要隐藏您的 IP 地址以及如何有效地做到这一点? 隐藏您的 IP 地址有助于保护您的在线匿名性。您的 IP 地址就像您的…...

nodejs 007:错误npm error Error: EPERM: operation not permitted, symlink
完整错误信息 npm error Error: EPERM: operation not permitted, symlink npm warn cleanup Failed to remove some directories [ npm warn cleanup [ npm warn cleanup C:\\Users\\kingchuxing\\Documents\\IPFS\\orbit-db-set-master\\node_modules\\ipfs-cli, npm…...

Rsync未授权访问漏洞复现及彻底修复
一、什么是 Rsync? Rsync 是一种广泛使用的文件传输工具,它允许系统管理员和用户通过局域网(LAN)或广域网(WAN)在计算机之间同步文件和目录。Rsync 支持通过本地或远程 shell 访问,也可以作为守…...

影刀RPA实战:网页爬虫之携程酒店数据
1.实战目标 大家对于携程并不陌生,我们出行定机票,住酒店,去旅游胜地游玩,都离不开这样一个综合性的网站为我们提供信息,同时,如果你也是做旅游的公司,那携程就是一个业界竞争对手,…...

【UCB CS61C】Lecture 5 - Floating Point
目录 引入浮点数(Floating Point)定点表示法(Fixed-Point Model)科学记数法(Scientific Notation)记数法间的转换 IEEE 754 二进制浮点数算术标准实现目标单精度浮点编码阶码字段(The Exponent …...

【Binlog实战】:基于Spring监听Binlog日志
【Binlog实战】:基于Spring监听Binlog日志 binlog的三种模式 MySQL 的二进制日志(binlog)有三种不同的格式,通常被称为 binlog 模式。这三种模式分别是 Statement 模式、Row 模式和Mixed 模式。 Statement 模式: 在 …...

鸿蒙OpenHarmony【轻量系统芯片移植】轻量系统STM32F407芯片移植案例
轻量系统STM32F407芯片移植案例 介绍基于STM32F407IGT6芯片在拓维信息[Niobe407]开发板上移植OpenHarmony LiteOS-M轻量系统,提供交通、工业领域开发板解决方案。移植架构采用Board与SoC分离方案,使用arm gcc工具链Newlib C库,实现了lwip、l…...

基于SpringBoot+定时任务实现地图上绘制车辆实时运动轨迹图
目录 1. 项目结构 2. Maven依赖配置 (pom.xml) 3. 实现后端服务 4. 配置文件 (application.properties) 5. 启动项目 6. 访问页面 实现基于北斗卫星的车辆定位和轨迹图的Maven工程(使用模拟数据),我们将使用以下技术: Spri…...

Rasa对话模型——做一个语言助手
1、Rasa模型 1.1 模型介绍 Rasa是一个用于构建对话 AI 的开源框架,主要用于开发聊天机器人和语音助手。Rasa 提供了自然语言理解(NLU)和对话管理(DM)功能,使开发者能够创建智能、交互式的对话系统。 1.2…...

golang学习笔记19——golang做服务发现与注册的深度剖析
推荐学习文档 golang应用级os框架,欢迎stargolang应用级os框架使用案例,欢迎star案例:基于golang开发的一款超有个性的旅游计划app经历golang实战大纲golang优秀开发常用开源库汇总想学习更多golang知识,这里有免费的golang学习笔…...

ROS和ROS2借助智能大模型的学习和研究方法
机器人相关知识的本身和价值-CSDN博客 知识本身在智能时代毫无价值,需要基于知识应用和创新才有价值。 学历报废并非来自扩招,而是智能模型的快速发展。-CSDN blink-领先的开发者技术社区 2024年中秋,智能模型实力已经如此,但还…...

弹性负载均衡ELB 详解和设置方法
一、弹性负载均衡ELB 详解 1. 定义与概念 弹性负载均衡(Elastic Load Balancing,简称ELB)是一种将访问流量自动分发到多台云服务器的流量分发控制服务。它通过在多个后端服务器之间均衡分配请求,提高应用程序的可用性、可扩展性…...

Python3网络爬虫开发实战(15)Scrapy 框架的使用(第一版)
文章目录 一、Scrapy 框架介绍1.1 数据流1.2 项目结构1.3 Scrapy 入门 二、Selector 解析器2.1 XPath 和 CSS 选择器2.2 信息提取2.3 正则提取 三、Spider 的使用3.1 Spider 运行流程3.2 Spider 类分析3.3 Request3.4 Response 四、Download Middleware 的使用4.1 process_requ…...

大众点评代发排名骗局
大众点评代发排名骗局 不诋毁同行,不贬低对手,请各位老板擦亮眼睛,认真看完这篇文章,以防上当受骗#网络宣传#企业推广#企业推广 大众点评代发排名:一场精心编织的骗局 在这个美食如云的时代&…...

硬件基础知识
驱动开发分为:裸机驱动、linux驱动 嵌入式:以计算机技术为基础,软硬结合的、可移植、可剪裁的专用计算机 单片机最小单元:vcc gnd reset 晶振 cpu --- soc :system on chip 片上外设 所有的程序都是在soc(cpu&…...

使用gitee如何回滚上一个版本,简单操作方式-gitee自带功能无需使用代码
使用gitee如何回滚上一个版本,简单操作方式-gitee自带功能无需使用代码,很多朋友使用代码的话容易出错,gitee自带了本功能: 找到gitee代码仓库,找到对应的想要回滚的版本点击进去 点击revert,选择自己对应的…...
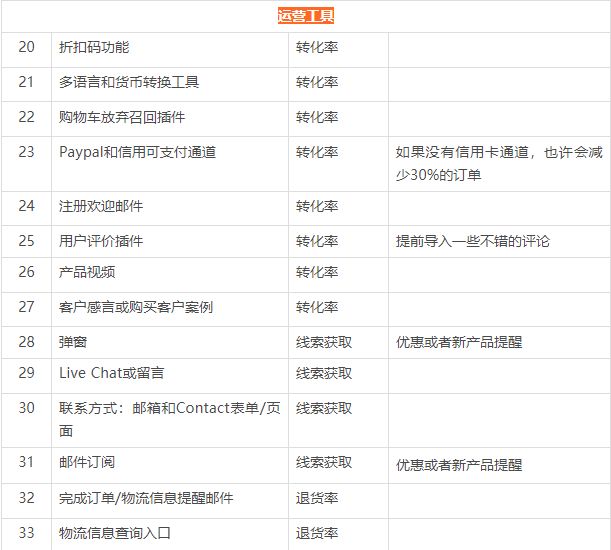
独立站技能树之建站33项自检清单 1.0丨出海笔记
很多时候大家建好站之后很嗨,但过一会就开始担忧各种纠结我是不是还有什么点没做好,或者我的站漏了什么东西,那么接下来以下这个独立站自检清单能很好的帮到你。其实对于新手我还是建议大家直接用一些模板,因为模板上面基本该有的…...

js进阶-作用域是什么
经过前面80多篇文章对js相关内容的讲解,相信大家对js这门语言已经有了一定的知识储备,也掌握了这门语言的相关特性,领会到这门语言的魅力所在,所以从今天开始,会定期更新js进阶相关知识,大家可以持续关注&a…...

ant-design表格自动合并相同内容的单元格
表格自动合并相同内容的单元格 合并hooks import { TableColumnProps } from antdexport const useAutoMergeTableCell <T extends object>(dataSource: Array<T>,columns: Array<TableColumnProps> | Array<keyof T> ): Map<keyof T, Array<…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...
