【UCB CS61C】Lecture 5 - Floating Point
目录
- 引入浮点数(Floating Point)
- 定点表示法(Fixed-Point Model)
- 科学记数法(Scientific Notation)
- 记数法间的转换
- IEEE 754 二进制浮点数算术标准
- 实现目标
- 单精度浮点编码
- 阶码字段(The Exponent Field)
- 尾数字段(The Significand Field)
- 双精度浮点编码
- 0 的表示
- 无穷的表示
- NaN 的表示
- 极小值的表示
- 浮点数的限制
- 浮点数的转换
- 比较与表达式转换
- 浮点数转换为十进制
- 科学记数法转换为浮点数
本文章系计算机体系结构课程 UCB CS61C: Great Ideas in Computer Architecture 的学习笔记。
引入浮点数(Floating Point)
- 位(bits)只能表示 2 的非负幂;因此,在此种表示方式下,其所能表达的至少是一个整数,不可能是分数。

定点表示法(Fixed-Point Model)
- 十进制下的小数点作为边界分割浮点数的整数与分数部分,可以很容易得知小数部分的每一位由以 10 为底的负数幂构成(例如,25.2406ten = 2 ⨉ 101 + 5 ⨉ 102 + 2 ⨉ 10-1 + 4 ⨉ 10-2 + 6 ⨉ 10-4)
- 推而广之,二进制下的小数点作为边界分割浮点数的非负幂与负数幂部分。

- 在这种表示法中,随着精度的提高,所能表达的范围正急剧减小,我们将小数点固定在左边若干位数字,然而小数点不应该是完全固定的,它应该是任意的,为解决这一问题,我们引入科学记数法。
科学记数法(Scientific Notation)
- 大致分为尾数(significand)和阶码(exponent)、基数(base)三大部分,可以通过阶码来更改小数点的位置(实际上二进制点是浮动的,因此也被称为浮点)。由于只允许小数点左边存在一位数字,我们通过规格化的科学记数法可以最大限度地利用有限的有效数字。

记数法间的转换
- 对于 x.xxxxtwo ⨉ 2n ,若 n > 0 n > 0 n>0 则浮点向右移动 n n n 位,若 n < 0 n < 0 n<0 则浮点向左移动 n n n 位,转换为一般固定点数。
- 一般固定点数转换为科学记数法的浮点数只需要逆向完成上述过程即可。
IEEE 754 二进制浮点数算术标准
实现目标
- 适配于所有计算机的实数标准算术:计算机对于实数的表示是近似的,我们希望相同的浮点数表达式求值在任何计算机上可以获取到相同的结果。
- 在较大的范围内保持尽可能高的精度。
- 帮助解决实数算术中的错误:
-
- + ∞ +\infty +∞, − ∞ -\infty −∞,Not-A-Number(NaN),指数溢出(包括上溢和下溢)
- 保证编码与二进制补码的兼容性。
-
- 例如,浮点数中的 +0 与二进制补码中的 0 一致
-
- 能够在不进行浮点比较(floating point comparison)的情况下排序
单精度浮点编码
对于以标准化科学记数法表示的二进制数 ± 1. x x x . . . x t w o × 2 y y y . . . y t w o \pm 1.xxx...x_{two} \times 2^{yyy...y} \ two ±1.xxx...xtwo×2yyy...y two:
- 将一个 32 位的字(word,32-bit 可以存储 4 个字节)分割为 3 个区域:
-
- 符号位(sign):占用 1 位,1 为负,0 为正
-
- 阶码(exponent):占用 8 位,代表 y y y,对浮点数加权
-
- 尾数(significand):占用 23 位,代表 x x x

- 二进制点本质上存储在阶码字段中;由于首部的 1 是固定的,我们不需要额外的区域来存储。
阶码字段(The Exponent Field)
- 为了便于浮点数间的大小比较,我们在阶码中引入移码(bias notation),当浮点数的实际值很小时,我们希望看起来也很小。在补码中,负数的补码表示是通过对其绝对值取反加一得到的,-1 的补码形式 11111111 看起来大于 0 的补码形式 00000000,所以这并不是一个好的选择;而移码则保留了值的线性关系(the linearity of value)。
- 对于若干个浮点数进行排序时,先查看符号位,正数将始终大于负数;随后查看阶码和尾数,二者如果具有相同的尾数,阶码越大浮点数本身越大,如果具有相同的阶码,则尾数越大浮点数本身越大。因而,我们基本上只需要使用无符号的比较。
- 在移码表示的指数值 e e e 满足实际指数值 E = e − b i a s E = e - bias E=e−bias,阶码存在正负,引入偏置值 b i a s = 2 k − 1 − 1 bias = 2^{k - 1} - 1 bias=2k−1−1,对于单精度浮点数来说, k = 8 k = 8 k=8,则 b i a s = 127 bias = 127 bias=127,因此,当移码取值范围 0(00000000two)~ 255(11111111two)时,实际的指数值取值范围 -127 ~ 128。
| 实际指数值 | 移码 | 十进制下的移码值 |
|---|---|---|
| 无穷大 | 11111111 | 255 |
| 127 | 11111110 | 254 |
| … | … | … |
| 2 | 10000001 | 129 |
| 1 | 10000000 | 128 |
| 0 | 0111111 | 127 |
| -1 | 0111110 | 126 |
| -2 | 0111101 | 125 |
| … | … | … |
| -126 | 00000001 | 1 |
| Denorms(无穷小) | 00000000 | 0 |
尾数字段(The Significand Field)
对于单精度浮点数,结构大致为 ( − 1 ) s × ( 1. S ) × 2 ( E − 127 ) (-1)^s \times (1.S) \times 2^{(E - 127)} (−1)s×(1.S)×2(E−127),其中 S S S 为尾数, E E E 为阶码:
- ( 1. S ) (1.S) (1.S) 可以看作尾数的值 + 1。
- 尾数表示所有 2 的负幂次,其总和总是小于 1.

双精度浮点编码
- 与单精度相同的结构,存储数据的空间扩大为 64 位,其中:
-
- 阶码占用扩大为 11 位
-
- 尾数占用扩大为 52 位
-
- 符号位占用保持不变

- 符号位占用保持不变
- C 声明变量类型为
double;阶码的偏置值 b i a s = 2 10 − 1 = 1023 bias = 2^{10} -1 = 1023 bias=210−1=1023,双精度意味着更高的精度,而非更大的范围。
0 的表示
- 由于隐含的 1 的出现,对于标准编码,
0x 00000000实际上是 1.0 ⨉ 10-27 ≠ 0。 - 特殊情况:当阶码和尾数均为 0 时,这一数值是真正的 0.
- 这意味着存在两个 0,基于数学的原因,我们希望知道一个数从符号位的正或负的一边趋近于 0.

无穷的表示
- 无穷被视为一个数字,并且可以进行比较与算术运算,例如
x / 0 > y。 - 取最高阶码 255,尾数均为 0

NaN 的表示
我们现在有如下的情形:
| 移码 | 尾数 | 意义 |
|---|---|---|
| 0 | 0 | ± \pm ± 0 |
| 0 | 非 0 | ? |
| 1-254 | 任意值 | ± \pm ± 浮点数 |
| 255 | 0 | ± ∞ \pm \infty ±∞ |
| 255 | 非 0 | ? |
- 阶码为 255,而尾数不为 0,实际上并不是一个数字(NaN):
-
- 0 0 \frac{0}{0} 00、 − 4 \sqrt{-4} −4、 ∞ − ∞ \infty - \infty ∞−∞、……
-
- 对于调试非常有帮助
-
- NaN 与数字的运算的结果仍为 NaN
- 取最高阶码 255,非零的尾数(可用于表示不同类型的 NaN):

极小值的表示
- 对于一个尽可能小的数字,符号位任取,阶码为最小值 1,尾数均为 0,即 a = 1.0...0 0 t w o × 2 1 − 127 = ( 1 + 0 ) × 2 − 126 = 2 − 126 . a = 1.0...00_{two} \times 2^{1 - 127} = (1+0) \times 2^{-126} = 2^{-126}. a=1.0...00two×21−127=(1+0)×2−126=2−126.
- 第二小的数字应为 b = 1.0...0 1 t w o × 2 1 − 127 = ( 1 + 2 − 23 ) × 2 − 126 = 2 − 126 + 2 − 149 . b = 1.0...01_{two} \times 2^{1 - 127} = (1+2^{-23}) \times 2^{-126} = 2^{-126} + 2^{-149}. b=1.0...01two×21−127=(1+2−23)×2−126=2−126+2−149.
- 介于 0 和 a a a 之间的数字是最接近 0 的。

- 0 到 a a a 的差值为 2 − 126 2^{-126} 2−126, a a a 到 b b b 的差值为 2 − 149 2^{-149} 2−149;前者远远大于后者,这是因为隐含的 1 的存在。因此,我们需要通过表示 0 到 a a a 的差值以内的值来表示极小值。
- 特殊情况:直接略去隐含的 1,当阶码等于 0 且尾数不为 0 时,即为非规格化数(denormalized numbers),所谓的尽可能接近于 0 的值。
- 非规格化数不包含隐含的 1,隐含的阶码为 -126(二进制点向前一位左移了一位,指数将会减少一位)。
- 最小的非规格化数为 ± 0 . 00...0 1 t w o × 2 − 126 = ± 2 − 149 \pm\textbf{0}.00...01_{two} \times 2^{-126} = \pm 2^{-149} ±0.00...01two×2−126=±2−149
- 最大的非规格化数为 ± 0 . 11...1 1 t w o × 2 − 126 = ± ( 2 − 126 − 2 − 149 ) \pm\textbf{0}.11...11_{two} \times 2^{-126} = \pm (2^{-126}-2^{-149}) ±0.11...11two×2−126=±(2−126−2−149)
那么,所有数值的情形就完备了:
| 移码 | 尾数 | 意义 |
|---|---|---|
| 0 | 0 | ± \pm ± 0 |
| 0 | 非 0 | 非规格化数 |
| 1-254 | 任意值 | ± \pm ± 浮点数 |
| 255 | 0 | ± ∞ \pm \infty ±∞ |
| 255 | 非 0 | NaN |
浮点数的限制
- 上溢(overflow):阶码(指数值)大于所能表示的值, ∣ x ∣ > 2 128 . |x| > 2^{128}. ∣x∣>2128.
- 下溢(underflow):负阶码(指数值)大于所能表示的值, 0 < ∣ x ∣ < 2 − 149 . 0< |x| < 2^{-149}. 0<∣x∣<2−149.

- 当算术结果超出了尾数所能容纳的范围,四舍五入(rounding)会出现并可能导致未意料的结果。浮点数有着不同的四舍五入模式,但最常见的是四舍五入到最近第一个可表示的浮点数——若算术结果位于规格化数与非规格化数的空隙(gaps)内,我们需要找出最近的一个浮点数,以此来表示。
- 空隙的宽度取决于阶码字段(exponent fields),如图,保持尾数的位数一致,当我们改变阶码时,空隙也随之发生改变。因此,每个可表示的浮点数之间的空隙是随着指数的增加而增大的。具体原因是:
-
- 标准化格式:随着数值的增大,指数位的值也会增加,而尾数的有效位数保持不变。
-
- 相对精度:浮点数的精度是相对的,通常是依据其值的大小来决定的。相邻的浮点数之间的差距与它们的大小成比例。
-
- 舍入误差:在浮点数运算过程中,可能会出现舍入误差,特别是在执行多次运算时,这些误差可能会累积。

- 因此,0 附近浮点数的值分布更密集且向两边越来越分散:

- 更大的取值范围并不意味着更多的数字,我们在增加阶码大小的同时丧失了一定的精度。解决这一问题的方案是使用更多的位数,这便是双精度浮点数出现的意义,大幅提高了精度。
- 浮点数的加法运算并不具有结合性(associative),这一问题基于舍入误差,尾数只有 23 位精度的浮点数不得不对结果进行近似,这同时也意味着看似简单的浮点运算将会无法得出准确的结果。
- 浮点数无法表示所有的整数。由于愈来愈宽的空隙,在某一点的空隙将会超过 1,从而无法完全表示所有整数。例如,对于 2 24 + 1 2^{24}+1 224+1,实际值为 16777217,然而浮点数将会返回 16777216。
浮点数的转换
比较与表达式转换

- 1 = 1.0 × 2 0 1=1.0 \times 2^0 1=1.0×20, 2 = 1.0 × 2 1 2=1.0 \times 2^1 2=1.0×21, 3 = 11 1 t w o = 1.1 × 2 1 . 3=111_{two}=1.1\times2^1. 3=111two=1.1×21.
- 1~2 之间有 23 位尾数空余, F P ( 1 , 2 ) = 2 23 FP(1,2)=2^{23} FP(1,2)=223;2~3 之间有一位被 1 占用, F P ( 2 , 3 ) = 2 22 . FP(2,3)=2^{22}. FP(2,3)=222.

- 第一个条件是成立的。当我们将两个浮点数相乘时,阶码相加,尾数相乘,并且不存在溢出,所以两边是等价的。
- 第二个条件是不成立的。右边的表达式中,
Big+BigNeg= 0,加上Tiny,原式即为Tiny;而左边的表达式中,当我们尝试将一个较大的数字Big与一个较小的数字Tiny相加时,阶码不会改变,只改变尾数(有效位数)。 因此当我们将 2 60 2^{60} 260 与 2 − 15 2^{-15} 2−15 相加时,需要更改二进制点后 75 位的尾数(Big至少是Tiny的 224 倍),然而尾数只有 23 位的长度,最终我们将不会添加任何内容。由此,左边的表达式将求值为 0.
浮点数转换为十进制

- 观察阶码字段,判断是否为非规格化数。上图所给出的表明其为规格化数(一般的浮点数)。
- 提取对应的信息,并代入科学记数法公式: ( − 1 ) s i g n × 1. s i g n i f i c a n d × 2 e x p o n e n t − 127 . (-1)^{sign} \times 1.significand \times 2^{exponent - 127}. (−1)sign×1.significand×2exponent−127. 由上图可知,
sign= 0,exponent=0b 0110 1000= 26 + 25 + 23 = 104,而尾数 1.101 0101 0100 0011 0100 0010 = 1 + 2 − 1 + 2 − 3 + 2 − 5 + 2 − 9 + 2 − 14 + 2 − 15 + 2 − 17 + 2 − 22 = 1.666115 1.101 \ 0101 \ 0100 \ 0011 \ 0100 \ 0010=1+2^{-1}+2^{-3}+2^{-5}+2^{-9}+2^{-14}+2^{-15}+2^{-17}+2^{-22}= 1.666115 1.101 0101 0100 0011 0100 0010=1+2−1+2−3+2−5+2−9+2−14+2−15+2−17+2−22=1.666115,代入公式得 1.66115 × 2 104 − 127 = 1.66611 5 t e n × 2 − 23 ≈ 1.986 × 1 0 − 7 . 1.66115 \times 2^{104-127}=1.666115_{ten} \times 2^{-23} \approx 1.986 \times 10^{-7}. 1.66115×2104−127=1.666115ten×2−23≈1.986×10−7.
科学记数法转换为浮点数
给出 − 2.340625 × 1 0 1 . -2.340625 \times 10^1. −2.340625×101.
- 去规格化:小数点右移一位,得到 -23.40625,这是为了便于将其转换为二进制形式的科学记数法。
- 将得到的去规格化形式的数分为整数和小数两大部分,分别转换:对于整数部分,23 = 16 + 4 + 2 + 1 = 10111two;对于小数部分,0.40625 = 0.25 + 0.125 + 0.03125 = 2-2 + 2-3 + 2-5 = 0.01101two.
- 将两个部分合并,同时进行规格化,即 10111.01101 = 1.011101101 ⨉ 24.
- 调整阶码偏差并转化为二进制。
exponent= 4 + 127 = 131 = 10000011two ,则最终浮点数如下图:


相关文章:

【UCB CS61C】Lecture 5 - Floating Point
目录 引入浮点数(Floating Point)定点表示法(Fixed-Point Model)科学记数法(Scientific Notation)记数法间的转换 IEEE 754 二进制浮点数算术标准实现目标单精度浮点编码阶码字段(The Exponent …...

【Binlog实战】:基于Spring监听Binlog日志
【Binlog实战】:基于Spring监听Binlog日志 binlog的三种模式 MySQL 的二进制日志(binlog)有三种不同的格式,通常被称为 binlog 模式。这三种模式分别是 Statement 模式、Row 模式和Mixed 模式。 Statement 模式: 在 …...

鸿蒙OpenHarmony【轻量系统芯片移植】轻量系统STM32F407芯片移植案例
轻量系统STM32F407芯片移植案例 介绍基于STM32F407IGT6芯片在拓维信息[Niobe407]开发板上移植OpenHarmony LiteOS-M轻量系统,提供交通、工业领域开发板解决方案。移植架构采用Board与SoC分离方案,使用arm gcc工具链Newlib C库,实现了lwip、l…...

基于SpringBoot+定时任务实现地图上绘制车辆实时运动轨迹图
目录 1. 项目结构 2. Maven依赖配置 (pom.xml) 3. 实现后端服务 4. 配置文件 (application.properties) 5. 启动项目 6. 访问页面 实现基于北斗卫星的车辆定位和轨迹图的Maven工程(使用模拟数据),我们将使用以下技术: Spri…...

Rasa对话模型——做一个语言助手
1、Rasa模型 1.1 模型介绍 Rasa是一个用于构建对话 AI 的开源框架,主要用于开发聊天机器人和语音助手。Rasa 提供了自然语言理解(NLU)和对话管理(DM)功能,使开发者能够创建智能、交互式的对话系统。 1.2…...

golang学习笔记19——golang做服务发现与注册的深度剖析
推荐学习文档 golang应用级os框架,欢迎stargolang应用级os框架使用案例,欢迎star案例:基于golang开发的一款超有个性的旅游计划app经历golang实战大纲golang优秀开发常用开源库汇总想学习更多golang知识,这里有免费的golang学习笔…...

ROS和ROS2借助智能大模型的学习和研究方法
机器人相关知识的本身和价值-CSDN博客 知识本身在智能时代毫无价值,需要基于知识应用和创新才有价值。 学历报废并非来自扩招,而是智能模型的快速发展。-CSDN blink-领先的开发者技术社区 2024年中秋,智能模型实力已经如此,但还…...

弹性负载均衡ELB 详解和设置方法
一、弹性负载均衡ELB 详解 1. 定义与概念 弹性负载均衡(Elastic Load Balancing,简称ELB)是一种将访问流量自动分发到多台云服务器的流量分发控制服务。它通过在多个后端服务器之间均衡分配请求,提高应用程序的可用性、可扩展性…...

Python3网络爬虫开发实战(15)Scrapy 框架的使用(第一版)
文章目录 一、Scrapy 框架介绍1.1 数据流1.2 项目结构1.3 Scrapy 入门 二、Selector 解析器2.1 XPath 和 CSS 选择器2.2 信息提取2.3 正则提取 三、Spider 的使用3.1 Spider 运行流程3.2 Spider 类分析3.3 Request3.4 Response 四、Download Middleware 的使用4.1 process_requ…...

大众点评代发排名骗局
大众点评代发排名骗局 不诋毁同行,不贬低对手,请各位老板擦亮眼睛,认真看完这篇文章,以防上当受骗#网络宣传#企业推广#企业推广 大众点评代发排名:一场精心编织的骗局 在这个美食如云的时代&…...

硬件基础知识
驱动开发分为:裸机驱动、linux驱动 嵌入式:以计算机技术为基础,软硬结合的、可移植、可剪裁的专用计算机 单片机最小单元:vcc gnd reset 晶振 cpu --- soc :system on chip 片上外设 所有的程序都是在soc(cpu&…...

使用gitee如何回滚上一个版本,简单操作方式-gitee自带功能无需使用代码
使用gitee如何回滚上一个版本,简单操作方式-gitee自带功能无需使用代码,很多朋友使用代码的话容易出错,gitee自带了本功能: 找到gitee代码仓库,找到对应的想要回滚的版本点击进去 点击revert,选择自己对应的…...
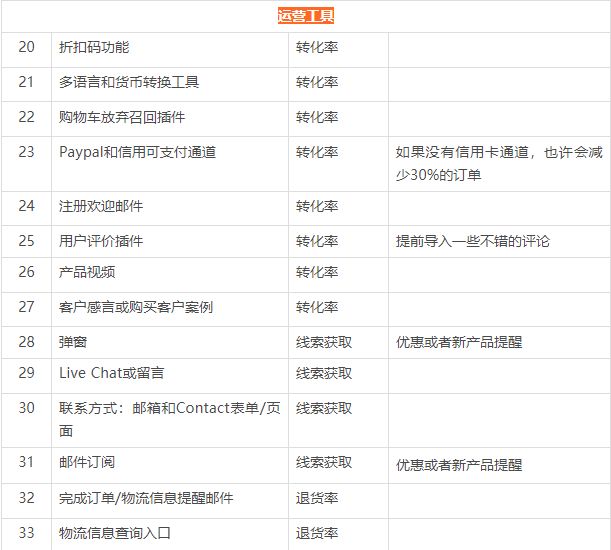
独立站技能树之建站33项自检清单 1.0丨出海笔记
很多时候大家建好站之后很嗨,但过一会就开始担忧各种纠结我是不是还有什么点没做好,或者我的站漏了什么东西,那么接下来以下这个独立站自检清单能很好的帮到你。其实对于新手我还是建议大家直接用一些模板,因为模板上面基本该有的…...

js进阶-作用域是什么
经过前面80多篇文章对js相关内容的讲解,相信大家对js这门语言已经有了一定的知识储备,也掌握了这门语言的相关特性,领会到这门语言的魅力所在,所以从今天开始,会定期更新js进阶相关知识,大家可以持续关注&a…...

ant-design表格自动合并相同内容的单元格
表格自动合并相同内容的单元格 合并hooks import { TableColumnProps } from antdexport const useAutoMergeTableCell <T extends object>(dataSource: Array<T>,columns: Array<TableColumnProps> | Array<keyof T> ): Map<keyof T, Array<…...
通过多模态关系图学习实现可解释的医学图像视觉问答|文献速递--Transformer架构在医学影像分析中的应用
Title 题目 Interpretable medical image Visual Question Answering via multi-modal relationship graph learning 通过多模态关系图学习实现可解释的医学图像视觉问答。 01 文献速递介绍 医学视觉问答(VQA)是医学多模态大语言模型(LL…...

从入门到精通,带你探索适合新手的视频剪辑工具
用视频来分享生活已经变成越来越多人的一种习惯,很多时候视频并不能一镜到底,所以还需要一些的修改、剪辑操作,那么这次我将介绍几款视频剪辑工具,希望能够让你分享的道路更加通畅。 1.FOXIT视频剪辑 连接直达>>https://w…...
)
线性规划------ + 案例 + Python源码求解(见文中)
目录 一、代数模型(Algebraic Models)详解1.1什么是代数模型?1.2代数模型的基本形式1.3 安装所需要的Python包--运行下述案例1.4代数模型的应用案例案例 1:市场供需平衡模型Python求解代码Python求解结果如下图:案例 2:运输问题中的线性规划模型进行数学建模分析1. 目标函…...

用Java实现人工智能
用Java实现人工智能 #Java #人工智能 #AI #机器学习 #深度学习 #数据科学 #技术博客 #编程技巧 文章目录 前言环境准备1. 安装Java2. IDE选择3. 依赖管理 数据准备模型训练模型评估分类模型评估回归模型评估模型的交叉验证 模型部署部署模型的基本步骤模型保存与加载Docker容器…...

MobaXterm使用技巧
引言 在现代IT环境中,远程管理和SSH连接已经成为管理员和开发者日常工作的重要组成部分。MobaXterm是一款功能强大的终端模拟器,它集成了多种网络工具,非常适合用于远程管理、编程和网络调试。本文将汇总一些MobaXterm的使用技巧,…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

CMake系统学习笔记
CMake系统学习笔记 基础操作 最基本的案例 // code #include <iostream>int main() {std::cout << "hello world " << std::endl;return 0; }// CMakeLists.txt cmake_minimum_required(VERSION 3.0)# 定义当前工程名称 project(demo)add_execu…...
